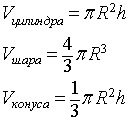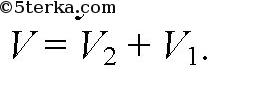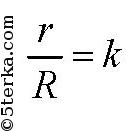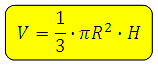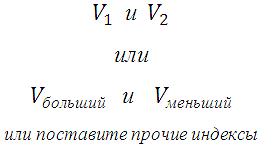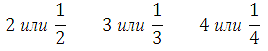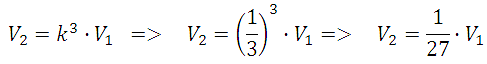Примечание. Это урок с решениями задач по геометрии (раздел стереометрия, конус). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме.
Задача.
В цилиндр вписаны шар и конус, причём высота цилиндра равна диаметру его основания.
Найти отношение объёма конуса к объёму шара, и к объёму цилиндра.
Решение.
Для решения задачи воспользуемся формулами нахождения объема шара, цилиндра и конуса:
Учтем, что по условию задачи высота цилиндра, а, соответственно и конуса, равны диаметру шара, что следует из построения согласно условию. То есть шар касается обеих оснований цилиндра в их центре. Из чего запишем:
h = 2R
Откуда
Vцилиндра = πR2h = πR22R = 2πR3
Vшара = 4/3πR3
Vконуса = 1/3πR2h = 1/3πR22R = 2/3πR3
Таким образом, соотношение объема конуса к объему шара будет равно:
Vконуса / Vшара = 2/3πR3 / 4/3πR3 = 2/3 / 4/3 = 1/2
А соотношение объема конуса к объему цилиндра будет равно:
Vконуса / Vшара = 2/3πR3 / 2πR3 = 2/3 / 2 = 1/3
Ответ: 1/2 и 1/3
Задача.
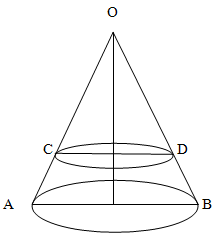
Объем конуса равен 27. На высоте конуса лежит точка и делит её в отношении 2:1 считая от вершины. Через точку проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение.
Обратим внимание, что треугольники AOB и COD — подобны. Из условия задачи определим коэффициент подобия как 2:3.
Объем конуса находится по формуле, указанной в предыдущей задаче.
Vконуса = 1/3πR2h = 27 (по условию)
Тогда объем малого конуса будет равен
Vмал.конуса = 1/3π(2/3R)2(2/3h)
то есть
Vмал.конуса = 1/3π 4/9 R2 2/3 h
Vмал.конуса = 8/27 *1/3π R2 h
а так как мы знаем, что 1/3π R2 h= 27 (см. выше), то
Vмал.конуса = 8/27 * 27 = 8
Ответ: объем малого конуса равен 8
0
Площадь боковой поверхности конуса |
Описание курса
| Объем конуса (2)
Дополним усеченный конус до полного. Тогда, если V0 — объем усеченного конуса, а V1 — объем конуса с радиусом r, то
Из подобия конусов следует, что если
то
Так что
Объём конуса. Вот мы с вами добрались до конусов и цилиндров. Ещё, кроме тех, что уже опубликованы, будет около девяти статей, рассмотрим все типы заданий. Если в течение года в открытый банк будут добавляться новые задачи, конечно же, они также будут размещены на блоге. В этой статье представлена теория, а в следующий будут примеры в которых она используется. Мало знать формулу объёма конуса, кстати вот она:
Можем записать:
Для решения некоторых примеров нужно понимать как соотносятся объёмы подобных тел. Именно понимать, а не просто выучить формулу:
То есть, если мы увеличим (уменьшим) линейные размеры тела в k раз, то отношение объёма полученного тела к объёму исходного будет равно k3.
ОБРАТИТЕ ВНИМАНИЕ! Не важно как вы обозначите объёмы:
Дело в том, что в процессе решения задач при рассмотре подобных тел, у некоторых может возникает путаница с коэффициентом k. Может появиться вопрос – Чему он равен?
(в зависимости от величины указанной в условии)
Всё зависит от того, с «какой стороны» посмотреть. Важно понимать вот что! Рассмотрим на примере – дан куб, ребро второго куба в три раза больше:
В данном случае, коэффициент подобия равен трём (ребро увеличено в три раза), а значит соотношение будет выглядеть следующим образом:
То есть объём полученного (большего) куба будет в 27 раз больше.
Можно посмотреть с другой стороны.
Дан куб, ребро второго куба в три раза меньше:
Коэффициент подобия равен одной трети (уменьшение ребра в три раза), а значит соотношение будет выглядеть:
То есть объём полученного куба будет в 27 раз меньше.
Заключение! Неважны индексы при обозначении объёмов, важно понимать как тела рассматриваются относительно друг друга.
Понятно, что:
— если исходное тело увеличивается, то коэффициент будет больше единицы.
— если исходное тело уменьшается, то коэффициент будет меньше единицы.
Про отношения объёмов можно сказать следующее:
— если в задаче будем делить объём большего тела на меньший, то получим куб коэффициента подобия, при чём сам коэффициент получится больше единицы.
— если будем делить объём меньшего тела на больший, то получим куб коэффициента подобия, при чём сам коэффициент получится меньше единицы.
Самое главное это запомнить – что когда речь идёт об ОБЪЁМАХ подобных тел, то коэффициент подобия имеет ТРЕТЬЮ степень, а не вторую, как в случае с площадями.
Ещё один момент касающийся конуса.
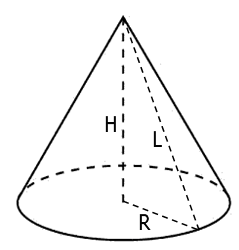
В условии присутствует такое понятие как образующая конуса. Это отрезок соединяющий вершину конуса с точками окружности основания (на рисунке обозначен буквой L).
Здесь стоит отметить, что разбирать задачи мы будем только с прямым конусом (далее просто конус). Образующие у прямого конуса равны
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Лучший ответ
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Среди многообразия геометрических тел одним из самых интересных является конус. Образуется он путем вращения прямоугольного треугольника вокруг одного из своих катетов.
Содержание
- Как найти объем конуса — основные понятия
- Объем конуса
- Примеры с различными типами конусов
- Формула для объема конуса
- Вычисление высоты конуса с угловыми функциями
- Формула для высоты, когда объем и основание известны
- Расчет высоты оболочки конуса с угловыми функциями
- Объем усеченного конуса
- Конус объема: какие базовые знания необходимы для расчета объема конуса?
- Конус тома: эти ошибки заставляют учеников снова и снова!
- Чтобы путать высоту с мужской линией
- Расчет со смешанными единицами
- Неправильный расчет базовой площади
- Неверное преобразование формулы объема
- Конус тома: 5 всеобъемлющих советов
- Конус объема: здесь вы получаете настройку справки
- Каков объем конуса?
- Так вы вычисляете объем конуса
- Вычислить радиус для данного объема
- Осевое сечение и конус как тело вращения
- Круговая поверхность кругового конуса
Как найти объем конуса — основные понятия
Перед тем, как начать вычисления объема конуса, стоит ознакомиться с основными понятиями.
- Круговой конус – основанием такого конуса является круг. Если в основании лежит эллипс, парабола или гипербола, то фигуры называются эллиптическим, параболическим или гиперболическим конусом. Стоит помнить, что два последних вида конуса имеют бесконечный объем.
- Усеченный конус – часть конуса, расположенная между основанием и плоскостью, параллельной этому основанию, находящейся между вершиной и основанием.
- Высота – перпендикулярный основанию отрезок, выпущенный из вершины.
- Образующая конуса – отрезок, соединяющий границу основания и вершину.
Объем конуса
Для расчета объема конуса применяется формула V=1/3*S*H, где S – площадь основания, H – высота. Так как основание конуса – круг, то его площадь находится по формуле S= nR^2, где n = 3,14, R – радиус окружности.
Примеры с различными типами конусов
Конусы эллипса, прямые. Конусы эллипса, косые. Для конуса обычно вычисляются следующие вещи. Для расчета базовой площади конуса используются обычные методы расчета. Если основание представляет собой круг, используйте формулу для области из расчета круга. Если базой является эллипс или какая-либо другая форма, вы должны использовать обычные методы расчета.
Формула для объема конуса
Базовая область требуется, например, Например, для вычисления объема. Поэтому должны быть доступны базовые знания о территориальных расчетах.
Вычисление высоты конуса с угловыми функциями
Высота конуса может быть рассчитана по-разному в пирамиде. Одна из возможностей – применить угловые функции.
Бывает ситуация, когда неизвестны какие-то из параметров: высота, радиус или образующая. В таком случае стоит прибегнуть к теореме Пифагора. Осевым сечением конуса является равнобедренный треугольник, состоящий из двух прямоугольных треугольника, где l – гипотенуза, а H и R – катеты. Тогда l=(H^2+R^2)^1/2.
Для этой цели в конусе образуется прямоугольный треугольник. В зависимости от длины и углов высота может быть рассчитана с помощью функций угла. В качестве альтернативы можно также применить теорему Пифагора. Угол не требуется, но требуются длины двух сторон.
Формула для высоты, когда объем и основание известны
Высота также может быть рассчитана, если известны объем и площадь основания конуса.
Расчет высоты оболочки конуса с угловыми функциями
Как и в случае с высотой, высоту куртки можно также рассчитать с помощью функций угла, если имеется необходимая информация. Здесь требуется только одна длина с двух сторон, а также угол.
Объем усеченного конуса
Усеченный конус представляет собой конус с обрезанной верхушкой.
Чтобы найти объем такого конуса понадобится формула:
V=1/3*n*H*(r^2+rR+R^2),
где n=3.14, r – радиус окружности сечения, R – радиус большого основания, H – высота.
В качестве альтернативы можно применить теорему Пифагора, если известны длины двух других сторон. В этом случае вам не нужен угол. В отличие от пирамиды нет края. С боулингом или боулином, каждый из нас уже провел свой вечер. В школе вам также нужно провести время с боулингом, но теперь в области космической геометрии и темы конуса. Этот текст определенно поможет вам.
Конусообразные пирамиды – сужающиеся тела. Острые тела имеют основание, а высота тела сверху вниз. Основание конуса всегда представляет собой круг. В реальной жизни, например, красно-белые шляпы на конусах – это конусы. Вы также найдете похожие шляпы на тренировке футбола.
Осевым сечением усеченного конуса будет равнобедренная трапеция. Поэтому, если необходимо найти длину образующей конуса или радиуса одной из окружностей, стоит применять формулы для нахождения боковых сторон и оснований трапеции.
Найти объем конуса, если его высота равна 8 см, радиус основания 3 см.
Дано: H=8 см, R=3 см.
Сначала найдем площадь основания, применив формулу S=nR^2.
Объем конуса на самом деле легко вычислить. Одна из трудностей состоит в том, что конус имеет вторую высоту, а именно боковую высоту. Но сначала посмотрите на следующее пояснительное видео, и если у вас все еще есть вопросы, просто прочитайте. Поскольку вам нужно рассчитать формулу объема в конусе и где осенние шнуры скрыты в следующем пояснительном видео.
Конус объема: какие базовые знания необходимы для расчета объема конуса?
Конус – это заостренное тело, которое видно на рисунке выше. Поэтому формула для объема конуса всегда такова. Высота кузова всегда проходит от кончика конуса, перпендикулярного к центру круглого основания. Таким образом, он образует угол 90 градусов вместе с радиусом основания.
S=3.14*3^2=28.26 см^2
Теперь по формуле V=1/3*S*H находим объем конуса.
V=1/3*28.26*8=75.36 см^3
Фигуры в форме конуса встречаются повсюду: парковочные конусы, башни строений, абажур светильника. Поэтому знание, как найти объем конуса, порой может пригодиться как в профессиональной, так и в повседневной жизни.
Это станет важным позже, потому что конус также всегда имеет так называемую Мантеллину, к которой может относиться высота конуса. Формула объема для конуса также может быть описана более подробно. С помощью этой формулы вы можете рассчитать объем конуса. Однако во многих задачах объем уже задан, и вам нужно рассчитать другие значения, такие как базовая площадь или высота конуса. Чтобы сделать это, вы должны изменить формулу, чтобы вы могли также вычислить желаемый результат. Здесь указаны две настройки формулы для базовой области и высоты.
Иногда в классной работе вам приходится вычислять высоту конуса, используя линию человека. Здесь вступает в игру теорема Пифагора. Высота конуса и радиус основания вместе с линией маневров образуют прямоугольный треугольник, линия маневров – гипотенуза, радиус и высота – два катета.
Добрались до конусов и цилиндров. Ещё, кроме тех, что уже опубликованы, будет около девяти статей, рассмотрим все типы заданий. Если в течение года в открытый банк будут добавляться новые задачи, конечно же, они также будут размещены на блоге. В этой статье представлено несколько примеров связанных с вычислением объёма. Мало знать формулу объёма конуса, кстати вот она:
Конус тома: эти ошибки заставляют учеников снова и снова!
Это приводит к следующему соотношению. Теперь вы действительно знаете все основы, чтобы осваивать тему объемных конусов. К счастью, вас больше нет.
Чтобы путать высоту с мужской линией
Объем конуса, который вы должны вычислить с ростом. Для излучения высота тела указывает, насколько высока кончик конуса над центром плоскости земли. Он стоит вертикально на базе!
Расчет со смешанными единицами
Мой совет: внимательно посмотрите на фигуру в задаче и пометьте ее соответствующими измерениями. Если в описании работы класса не указан чертеж, а данные находятся только в текстовой форме, затем создайте эскиз и отметьте его. Нередко учащиеся получают неверные результаты, хотя они действительно правильно рассчитаны. Если это случилось с вами, то вы, конечно, не были осторожны в задаче, которую вы вычисляете с помощью единых единиц измерения. Счетчики могут измеряться только метрами и сантиметрами с сантиметрами и т.д. если вы не обратили на вас внимания с пресловутыми яблоками и грушами, результат будет неправильным.
Можем записать:
Нужно ещё понимать как соотносятся объёмы подобных тел. Именно понимать, а не просто выучить формулу. Вот она сама:
Неправильный расчет базовой площади
Мой совет: маркированные рисунки и эскизы так же, как вы объединяете единицы измерения, тогда ошибка здесь не может быть. Базовая область круга всегда является горячим кандидатом на ошибки в работе класса. Студентам нравится путать окружность круга с круговой областью. Если вы хотите рассчитать объем с формулой для окружности круга, конечно, дерьмо выйдет. Мой совет: помните, что круг вычисляется по следующей формуле.
Неверное преобразование формулы объема
Как упоминалось выше, при работе в классе часто вы указываете объем, и вам нужно рассчитать либо базовую площадь, либо высоту конуса. Здесь студенты часто ошибаются при изменении формулы объема. Мой совет: напишите конверсии формулы объема в зависимости от результата, который вы должны рассчитать прямо в начале задания, тогда вам нужно только записать его, если вам нужно использовать значения и полностью сосредоточиться на нем. И здесь два соотношения формулы.
То есть, если мы увеличим (уменьшим) линейные размеры тела в k раз, то отношение объёма полученного тела к объёму исходного будет равно k 3 .
ОБРАТИТЕ ВНИМАНИЕ! Не важно как вы обозначите объёмы:
Конус тома: 5 всеобъемлющих советов
Обозначьте фигуру в спецификации работы класса с правильными единицами измерения! В спецификации работы класса проверьте, какие размеры вы указали! Не путайте линию с высотой конуса! Поместите данные измерения в ваши формулы!
Конус объема: здесь вы получаете настройку справки
- Если у вас нет рисунка, сделайте эскиз и отметьте его!
- Внимание: сначала отрегулируйте единицы измерения!
- Напишите формулы, необходимые для расчета объема с помощью конуса!
- Подумайте об изменениях, когда вы должны рассчитать высоту или базу!
Как насчет, если вы можете четко и легко повторить тему объемных конусов?
Дело в том, что в процессе решения задач при рассмотре подобных тел, у некоторых может возникает путаница с коэффициентом k. Может появиться вопрос – Чему он равен?
(в зависимости от величины указанной в условии)
Всё зависит от того, с «какой стороны» посмотреть. Важно понимать вот что! Рассмотрим на примере – дан куб, ребро второго куба в три раза больше:
Каков объем конуса?
Хотели бы вы учиться с помощью реальной классовой работы и подробных объяснений и решений для следующего экзамена? Вы знаете конусы со строительных площадок на дороге. Конические конусы или башни крыши также конические. Круг как основание, куполообразное пальто и наконечник. . Соединительная линия от окружности до наконечника называется мантийной линией. Поскольку конус является телом, его можно заполнить.
Вы наполняете конус водой и измеряете его в измерительном стакане. Таким образом, вы получаете объем конуса. Объем говорит вам, сколько жидкости вписывается в конус. Для всех заостренных тел, а также пирамиды, вычислите объем с площадью основания, умноженной на 3 на 3.
В данном случае, коэффициент подобия равен трём (ребро увеличено в три раза), а значит соотношение будет выглядеть следующим образом:
То есть объём полученного (большего) куба будет в 27 раз больше.
Можно посмотреть с другой стороны.
Так вы вычисляете объем конуса
Для расчета объема конуса. Чтобы вычислить объем конуса, действуйте следующим образом. Вставьте данные значения в нашу формулу.
Вычислить радиус для данного объема
Чтобы вычислить радиус конуса, действуйте следующим образом. Вы также можете изменить формулу, а затем использовать громкость.
Круговой конус представляет собой геометрическое тело с кругом в качестве основания. В прямом конусе все линии имеют одинаковую длину, а мантия – круглый. Все остальные конусы называются косыми конусами. говорить прямой конус прямой конус говорить. Кроме того, прямолинейный круговой конус кратко называют конусом. Если упоминается косой конус, это прямо упоминается.
Дан куб, ребро второго куба в три раза меньше:
Коэффициент подобия равен одной трети (уменьшение ребра в три раза), а значит соотношение будет выглядеть:
То есть объём полученного куба будет в 27 раз меньше.
Заключение! Неважны индексы при обозначении объёмов, важно понимать как тела рассматриваются относительно друг друга.
С помощью формулы для расчета объема вы также можете рассчитать другие размеры конуса. Поверхность конуса. То есть, если высота умножается на коэффициент, объем умножается на тот же коэффициент. В конусе существует также функциональная зависимость между радиусом и объемом. То есть, если радиус умножается на множитель, объем умножается на квадрат этого фактора. Полый конус образуется, когда меньший конус вырезается из конуса.
Осевое сечение и конус как тело вращения
Ниже рассматриваются полые конусы, в которых оба конуса имеют одинаковую ось симметрии. Объем полого конуса получается путем вычитания объема меньшего конуса из объема большего конуса. Если конус разрезан вдоль плоскости, на которой лежит ось симметрии, создается осевое сечение конуса.
Понятно, что:
— если исходное тело увеличивается, то коэффициент будет больше единицы.
— если исходное тело уменьшается, то коэффициент будет меньше единицы.
Про отношения объёмов можно сказать следующее:
— если в задаче будем делить объём большего тела на меньший, то получим куб коэффициента подобия, при чём сам коэффициент получится больше единицы.
Если прямоугольный треугольник вращается вокруг катетера, конус создается как тело вращения. Если подходящая трапеция вращается вокруг одной стороны, в качестве тела вращения образуется полый конус. Усеченный конус образуется, когда конус вырезан параллельно основанию.
Все эти меры могут быть рассчитаны с этими коэффициентами. Круговой конус представляет собой геометрическое тело, которое выглядит как смесь цилиндра и пирамиды. Он имеет круглую основу, подобную цилиндру, и наконечник, подобный пирамиде. Кончик конуса расположен чуть выше центра основания. Поверхность куртки является круглым вырезом.
— если будем делить объём меньшего тела на больший, то получим куб коэффициента подобия, при чём сам коэффициент получится меньше единицы.
Самое главное это запомнить – что когда речь идёт об ОБЪЁМАХ подобных тел, то коэффициент подобия имеет ТРЕТЬЮ степень, а не вторую, как в случае с площадями.
Ещё один момент касающийся .
Круговая поверхность кругового конуса
Основание конуса рассчитывается как площадь нормального круга. Для этого расчета нам нужен только радиус. Окружность и площадь основания. Поверхность этого мнимого круга описывается. Окружность мнимой окружности, круговой вырез которой является боковой поверхностью, описывается.
Если мы установим окружность, чтобы круглый разрез, покрывающий пропорционально кругу большого круга, получим следующее. Если положить этот член до формулы для вычисления поверхности большого круга, мы получим поверхность кругового разреза. Теперь мы можем рассчитать площадь поверхности.
В условии присутствует такое понятие как образующая конуса. Это отрезок соединяющий вершину конуса с точками окружности основания (на рисунке обозначен буквой L).
Здесь стоит отметить, что разбирать задачи мы будем только с прямым конусом (далее просто конус). Образующие у прямого конуса равны.
Рассмотрим задачи:
72353. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Поверхность кругового конуса представляет собой сумму основания и поверхности оболочки. Объем конуса вычисляется по аналогии с объемом пирамиды. В дополнение к радиусу вам нужна высота при расчете объема. Конус – это фигура, которая генерируется вращением вокруг одной из ее ножек. Здесь вы узнаете, как рассчитать его объем. Объем – это место тела в космосе.
На следующем рисунке показано. Генератором является гипотенуза правильного треугольника. Чтобы рассчитать объем конуса, вы должны знать, формула которого равна. Где базовая площадь конуса. Объем конуса – третья часть объема цилиндра. Поэтому формула выглядит следующим образом.
Сразу отметим, что исходный и отсечённый конус подобны и если рассматривать отсечённый конус относительно исходного, то можно сказать так: меньший конус подобен большему с коэффициентом равным одной второй или 0,5. Можем записать:
Можно было записать:
Можно было рассудить так!
Рассмотрим исходный конус относительно отсечённого. Можно сказать – больший конус подобен отсечённому с коэффициентом равным двум, запишем:
Теперь посмотрите решение без использования свойств подобия.
Объём конуса равен одной трети произведения площади его основания и высоты:
Рассмотрим боковую проекцию (вид сбоку) с указанным сечением:
Пусть радиус большего конуса равен R, высота равна Н. Сечение (основание меньшего конуса) проходит через середину высоты, значит его высота будет равна Н/2. А радиус основания равен R/2, это следует из подобия треугольников.
Запишем объём исходного конуса:
Объём отсечённого конуса будет равен:
Столь подробные решения представлены для того, чтобы вы видели как можно выстроить рассуждения. Действуйте любым способом – главное, чтобы вы понимали суть решения. Пусть путь, который вы выбрали будет не рационален, важен результат (верный результат).
Ответ: 1,25
318145. В сосуде, имеющем форму конуса, уровень жидкости достигает половину высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Данная задача схожа с предыдущей. Хоть речь здесь и идёт о жидкости, принцип решения один и тот же.
Имеем два конуса – это сам сосуд и «малый» конус (наполненный жидкостью), они являются подобными. Известно, что объёмы подобных тел соотносятся следующим образом:
Исходный конус (сосуд) подобен конусу наполненному жидкостью с коэффициентом равным 2, так как сказано, что уровень жидкости достигает половину высоты. Можно записать подробнее:
Вычисляем:
Таким образом, долить нужно:
Ответ: 490
Другие задачи с жидкостями .
74257. Найдите объем V конуса, образующая которого равна 44 и наклонена к плоскости основания под углом 30 0 . В ответе укажите V/Пи.
Объем конуса:
Высоту конуса найдем по свойству прямоугольного треугольника.
Катет лежащий против угла 30° равен половине гипотенузы. Гипотенуза, в данном случае, является образующей конуса. Следовательно высота конуса равна 22.
Квадрат радиуса основания найдем по теореме Пифагора:
*Нам нужен квадрат радиуса, а не сам радиус.
Тогда объем будет равен: