Как найти собственные значения матрицы гессе

Решение проблемы обнаружения центральной линии сосуда

Суть задачи

В процессе медицинской диагностики может возникнуть необходимость исследовать сосуды пациента. Такое исследование называется ангиографией. С появлением томографов в дополнение к классической ангиографии появились методы МРТ и КТ ангиографии, которые в отличие от традиционной ангиографии, дающей только плоскую картинку в одной проекции, позволяют получить полное трехмерное представление сосудов. Для проведения таких исследований пациенту в кровь вводится контраст — специальное вещество, делающее сосуды на снимках более яркими. В зависимости от предполагаемого диагноза, врач или оценивает общую картину, или пытается найти конкретные участки сосудов, в которых возникли проблемы. Если участок сосуда сужен и пропускает меньше крови, чем должен, то это место называется стенозом.

Одна из задач врача — найти стенозы и оценить, насколько они опасны. Задача же разработчика, как обычно, облегчить работу конечного пользователя. Для этого необходимо построить полную 3D модель стенок сосуда и провести их первичный анализ. Это является большой и интересной задачей, однако, в её основе лежит более простая и известная проблема — построение центральной линии сосуда.

Первая попытка

Перед продолжением чтения этой статьи желательно чуть-чуть ознакомиться с представлением данных, получаемых в результате работы томографов. Это можно сделать, прочитав нашу давно написанную статью про воксельный рендер DICOM Viewer изнутри. Если коротко: есть 3D-массив чисел, в каждом элементе которого хранится значение сигнала (интенсивность). Этот массив называется объемом. Сам элемент является вокселем, а его индексы в 3D-массиве будут являться 3D-координатами. Перед рендером каждого вокселя, его интенсивность обрабатывается функцией, и воксель приобретает определенные цвет, яркость и прозрачность.

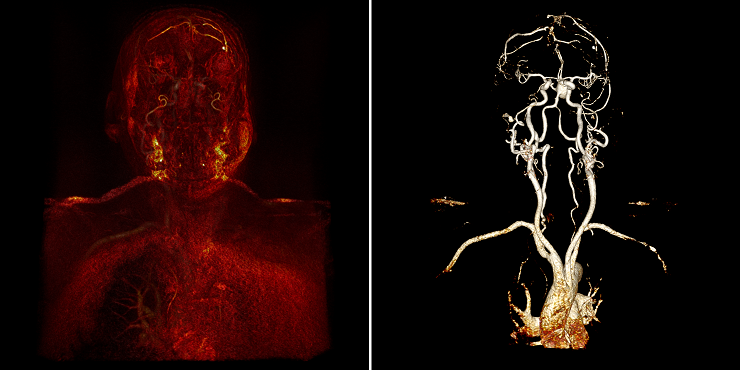
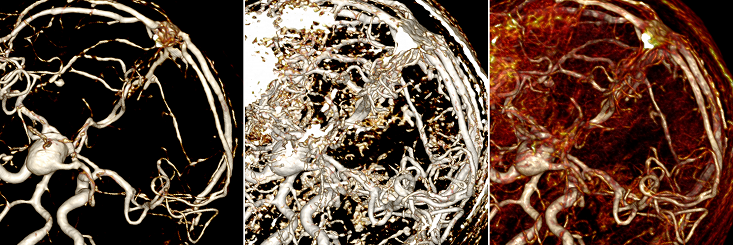
Относительно задачи, первое с чем столкнулся именно я — это то, что наш рендер позволяет уже на визуальном уровне показать все сосуды. А именно, из непонятной “каши”, как на рисунке слева, поигравшись с настройкам можно сделать вполне очевидные сосуды, как на рисунке справа:

Кажется, что задача решена: сосуды “вот они”, на ум сразу приходит region growing алгоритм: мы знаем цвет и прозрачность нужных нам вокселей, значит можно итерационно перебирать их соседей, пока не будет проложен путь между указанными точками.

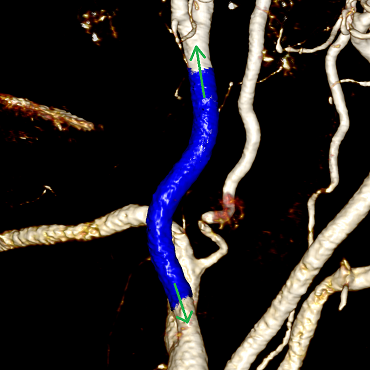
К тому же приходит идея, что если разобраться с ветвлениями, то можно вытянуть всю сеть сосудов. Но в действительности не всё так просто. Сосуд может вплотную прилегать к костям (их воксели идентичны по цветам, поэтому кость будет воспринята частью сосуда):

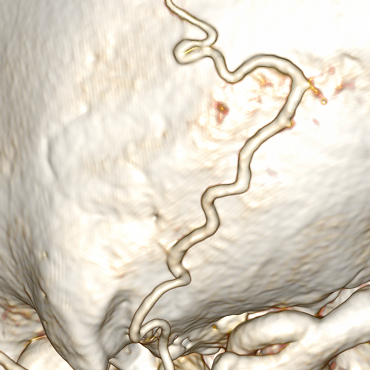
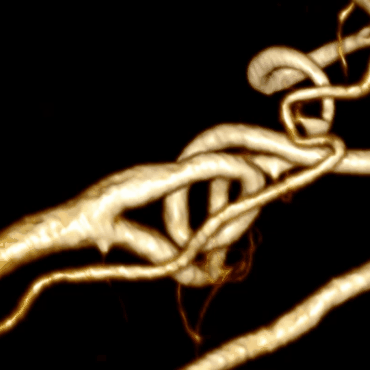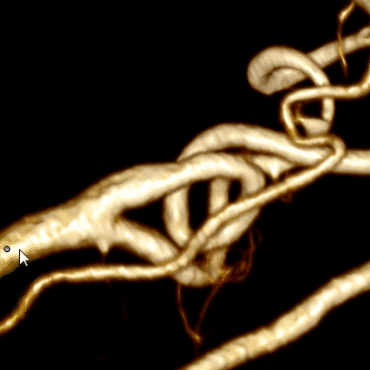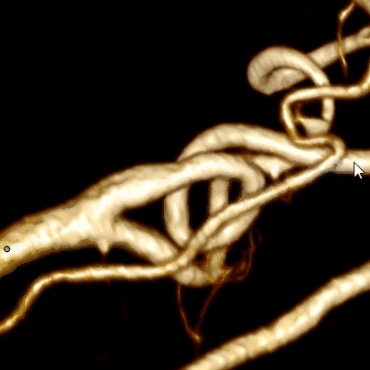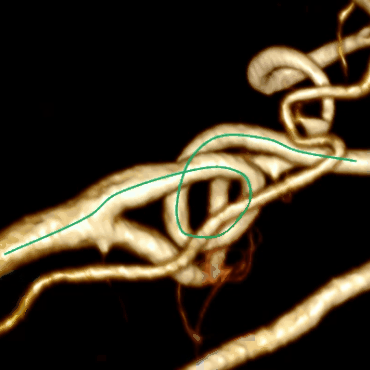
Сосуд может загибаться или прилегать вплотную к самому себе:

Участки сосуда могут быть очень тонкими и даже прерываться:

Нахождение оптимальных настроек рендера нетривиально. Пользователь может менять так называемое окно, и не существует конкретного значения окна, подходящего для всех сосудов хотя бы одного и того же исследования. Окно приходится каждый раз подгонять под конкретный случай. Ниже приведены три варианта одного и того же места с разными настройками:

В итоге приходим к тому, что интуитивно кажущийся верным алгоритм нужно либо дорабатывать, либо следует попробовать совершенно иной подход. После большого количества неудачных попыток пришлось пробовать что-то иное.

Классический подход

Основной подход к проблеме обнаружения сосудов (vessel detection), заключается в вычислении собственных значений матрицы Гессе (Hessian matrix). Также в последнее время к этой задаче пробуют подключить нейронные сети. Однако, стандартное решение выглядит более надежным, потому что имеет упоминание в большем количестве литературы и используется не только для нахождения сосудов, но и для многих других задач (например, обнаружение объектов на астрономических снимках), поэтому от нейронных сетей пришлось отказаться.

В нашем случае матрица Гессе — это матрица, элементами которой являются частные производные второго порядка интенсивности в конкретном вокселе:

— соответственно, вторые частные производные.

После построения матрицы Гессе необходимо найти её собственные значения и собственные векторы решив следующее уравнение:

— собственные значения. Задача их нахождения сводится к решению кубического уравнения, но в нашем случае матрица симметрична, поэтому решение упрощается и может быть представлено небольшим псевдокодом:

p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2
if (p1 == 0) 
   eig1 = A(1,1)
   eig2 = A(2,2)
   eig3 = A(3,3)
else
   q = trace(A)/3
   p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1
   p = sqrt(p2 / 6)
   B = (1 / p) * (A - q * I)
   r = det(B) / 2

   if (r <= -1) 
      phi = pi / 3
   else if (r >= 1)
      phi = 0
   else
      phi = acos(r) / 3
   end

   eig1 = q + 2 * p * cos(phi)
   eig3 = q + 2 * p * cos(phi + (2*pi/3))
   eig2 = 3 * q - eig1 - eig3
end

Где A — исходная матрица 3х3; I — единичная матрица 3х3; eig1, eig2, eig2 — собственные значения; trace() — возвращает след матрицы; det() — возвращает детерминант матрицы.

Теперь мы можем найти собственные векторы. Для этого в уравнение:

подставим одно из найденных собственных значений вместо . Найденный вектор и будет являться собственным вектором. Таких векторов получится три: — по одному для каждого собственного значения. Собственные значения и векторы необходимо отсортировать в таком порядке , при этом векторы тоже меняются местами, т.е. меняя местами значения и мы также меняем местами и . Если после сортировки выполняется условие , то считается, что воксель, в котором построили матрицу, принадлежит сосуду. При этом собственный вектор будет указывать направление вдоль сосуда независимо от того как близко к стенке находится воксель:

Если воксель принадлежит сосуду, то на основании собственных значений матрицы рассчитывается так называемая сосудистость. В литературе встречается очень много разных формул, и мы адаптировали под себя одну из них:

— соответственно, значение сосудистости

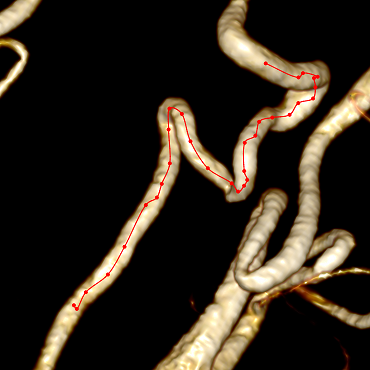
Чем больше сосудистость, тем ближе воксель к центру сосуда. Теперь несложно представить простой алгоритм поиска центральной линии из заданного вокселя:

1. Определяем направление сосуда в текущем вокселе,
2. Делаем перпендикулярный направлению срез сосуда и перемещаемся по градиенту в воксель среза с максимальной сосудистостью,
3. Определяем направление сосуда в вокселе с максимальной сосудистостью,
4. Делаем небольшой шаг в направлении сосуда и попадаем в новый воксель,
5. Возвращаемся в шаг 1.

Из первоначальной точки движение происходит в двух направлениях, потому что мы не можем заранее знать, какое из них нам нужно:

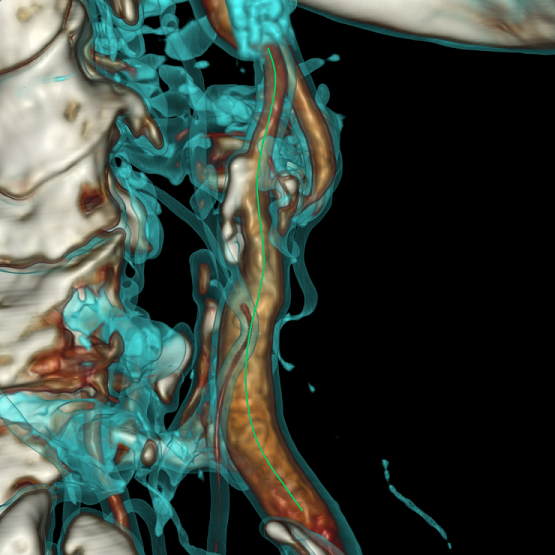
В результате получаем не самую красивую, но корректную центральную линию:

Чтобы центральная линия стала менее угловатой, необходимо отказаться от целочисленных координат вокселей и перейти к дробным координатам точек в 3D-пространстве, также можно выполнить небольшое сглаживание центральной линии после построения.

Для перехода к дробным координатам мы воспользовались бикубической интерполяцией при получении значений интенсивности. Общее уравнение фильтра в одномерном пространстве выглядит так:

где и имеют предопределенные значения. Если , то мы имеем дело с B-сплайном, если , то с кардинальным сплайном. В нашем случае , (Catmull-Rom filter). Тогда получаем:

Рассмотрим случай для 1D. Если даны значения в точках c координатами , и мы интерполируем , где , то мы можем вычислить вес для каждой вершины:

Итоговое проинтерполированное значение:

Теперь рассмотрим наш полноценный случай для 3D пространства. Как нетрудно догадаться, мы будем интерполировать внутри куба размерностью 4х4х4 вокселя. За основу берем веса, рассмотренные для 1D случая:

где — дробные координаты точки, — интенсивность в вокселе с координатами , — округление в меньшую сторону.

Для кого-то может показаться интересным факт, что сумма весов всех вокселей равна 1:

Детали

Вернемся к вычислению производных для матрицы Гессе. У нас есть координаты и интенсивность, как численно считается вторая частная производная все знают: основным является метод конечных разностей. Для точки :

Для устранения шума перед вычислением производных необходимо выполнить сглаживание Гаусса с некоторым значением и только потом вычислять матрицу Гессе в конкретной точке уже по сглаженным значениям интенсивности. Сглаживание Гаусса в точке:

где возвращает значение интенсивности в точке ; обычно принимает значение ( — округление в большую сторону); — коэффициент сглаживания.

Значения интенсивности в перпендикулярном срезе сосуда до сглаживания, после сглаживания, на третьем рисунке значения сосудистости:

При этом, чем большее значение мы используем, тем более толстые сосуды мы пробуем найти. А поскольку нам нужны вообще все сосуды — и тонкие, и толстые, то нам нужно много значений , и для каждого значения нам следует выполнить сглаживание. Мы остановились на диапазоне , который включает в себя 10 значений.

Однако, с ростом уменьшаются значениях вторых производных. Это, в свою очередь, приводит к тому, что сосудистость, рассчитанная с большой , оказывается меньше сосудистости, рассчитанной в той же точке с маленькой , даже если в действительности мы имеем дело с толстым сосудом. Получается, что независимо от реальной картины всегда преобладают структуры, напоминающие тонкие сосуды. Поэтому возникает вопрос: как соотнести друг с другом все полученные сосудистости для каждой из ? Для этого необходимо выполнить нормализацию между результатами вычислений. В литературе обычно проводятся манипуляции с полученной сосудистостью, например:

, где — нормализованная сосудистость, — сосудистость, полученная для сглаживания с , подбирается экспериментально, хороший вариант 0.5.

Мы же воспользовались так называемой гамма-нормализацией: , где — матрица Гессе, — порядок производной, т.е. 2, подбирается экспериментально, в нашем случае хорошо себя показал вариант 0.5. Тогда вся формула сводится к .

Теперь, если мы попытаемся вычислить значение сосудистости с маленькой в центре идеально тонкого сосуда, то оно будет примерно равно значению сосудистости с большой для центра идеально толстого сосуда.

Алгоритм вычислений для произвольной точки при построении центральной линии выглядит так:

2. Рассчитать собственные векторы матрицы Гессе, для которой сосудистость оказалась максимальной, и получить вектор-направление сосуда.

Совмещая этот алгоритм с алгоритмом построения центральной линии мы получим финальный результат:

Оптимизация

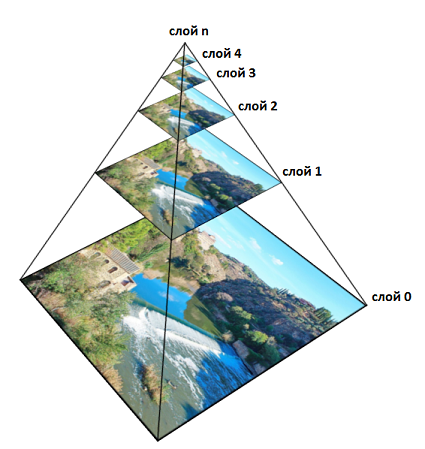
Описанный выше подход будет работать прекрасно, но есть несколько моментов. Во-первых, для повышения производительности сглаживание необходимо заранее выполнять сразу для всех вокселей и для всех . Во-вторых, с учетом того, что исследования обычно имеют размер примерно 512х512х512 вокселей, размер памяти, требуемой для хранения результатов сглаживания, в среднем будет занимать около 5 Гб. Чтобы сократить количество расходуемой памяти мы воспользовались пирамидой (scale space pyramid).

Идея заключается в том, что раз уж после каждого сглаживания значения интенсивности в соседних вокселях размываются и становятся примерно равными, то нет смысла хранить их все. Т.е. чем больше , тем меньше нам потом потребуется просчитанных вокселей, чтобы восстановить сглаживание по всему объему.

В общем случае работает это так. Нулевой слой объема является оригинальным. Вдоль каждой из осей объема несколько раз применяется сглаживающий фильтр (¼, ½, ¼), и после размерность объема уменьшается в два раза. Полученный объем будет принадлежать первому слою. Затем операция повторяется и получается второй слой. Потом третий и т.д. Каждому слою соответствует определенное значение . Пример для 2D:

Нетрудно посчитать, что в 3D суммарное количество памяти будет равно , где — количество памяти, требуемое для хранения оригинального объема. Однако, использование пирамиды таит в себе очень много трудностей и проблем, с которыми мы столкнулись, и которые тянут на отдельную статью, если про них рассказывать.

Итог

Можно считать изложенный подход построения центральной линии крайне эффективным, но он обладает некоторыми недостатками:

1. Для КТ исследований не удается обнаружить сосуды, которые проходят внутри костей (как, например, в позвоночнике)
2. Не всегда удается обнаружить сосуды, если они проходят вблизи вытянутых продолговатых костей, тканей или структур (в таких случаях кости, ткани и структуры сами могут ошибочно приниматься за сосуды)
3. Узким местом являются бифуркации (раздвоения сосудов)

Проблемы 1 и 2 решаются путем вычитания костей. Для этого необходимо два КТ исследования — с контрастом и без. Понятно, что единственным отличием таких исследований будут являться подсвеченные сосуды. Другими словами, если вычесть интенсивность каждого вокселя исследования без сосудов из интенсивности каждого вокселя исследования с сосудами, то в результате ненулевую интенсивность будут иметь только воксели, относящиеся к сосудам. Но поскольку два исследования нельзя сделать с абсолютно одинаковым положением тела пациента, то главной проблемой становится совмещение двух исследований в 3D-пространстве. Для этого используется трансформация поворотом и смещением. Ориентация в пространстве идет по костям, т.к. они представляют собой жесткие структуры. Для нахождения костей мы воспользовались очень интересным алгоритмом водопадов, основанных на графах (waterfall based on graphs).

Проблема бифуркаций же решается указанием начальной и конечной точек сосуда, между которыми необходимо построить центральную линию. Ее нужно начать строить в каждой из двух точек в каждом из двух направлений, а при пересечении центральных линий просто объединить их в одну. Т.к. сосуды ветвятся только в одном направлении (более толстые разбиваются на более мелкие в случае артерий, и более тонкие объединяются в более толстые в случае вен), то такой подход позволяет соединить две заданных точки.

На этом все, спасибо за внимание. На всякий случай ссылка на продукт.

From Wikipedia, the free encyclopedia

In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term «functional determinants».

Definitions and properties[edit]

Suppose is a function taking as input a vector and outputting a scalar If all second-order partial derivatives of exist, then the Hessian matrix of is a square matrix, usually defined and arranged as

That is, the entry of the ith row and the jth column is

If furthermore the second partial derivatives are all continuous, the Hessian matrix is a symmetric matrix by the symmetry of second derivatives.

The determinant of the Hessian matrix is called the Hessian determinant.^[1]

The Hessian matrix of a function is the transpose of the Jacobian matrix of the gradient of the function ; that is:

Applications[edit]

Inflection points[edit]

If is a homogeneous polynomial in three variables, the equation is the implicit equation of a plane projective curve. The inflection points of the curve are exactly the non-singular points where the Hessian determinant is zero. It follows by Bézout’s theorem that a cubic plane curve has at most inflection points, since the Hessian determinant is a polynomial of degree

Second-derivative test[edit]

The Hessian matrix of a convex function is positive semi-definite. Refining this property allows us to test whether a critical point is a local maximum, local minimum, or a saddle point, as follows:

If the Hessian is positive-definite at then attains an isolated local minimum at If the Hessian is negative-definite at then attains an isolated local maximum at If the Hessian has both positive and negative eigenvalues, then is a saddle point for Otherwise the test is inconclusive. This implies that at a local minimum the Hessian is positive-semidefinite, and at a local maximum the Hessian is negative-semidefinite.

For positive-semidefinite and negative-semidefinite Hessians the test is inconclusive (a critical point where the Hessian is semidefinite but not definite may be a local extremum or a saddle point). However, more can be said from the point of view of Morse theory.

The second-derivative test for functions of one and two variables is simpler than the general case. In one variable, the Hessian contains exactly one second derivative; if it is positive, then is a local minimum, and if it is negative, then is a local maximum; if it is zero, then the test is inconclusive. In two variables, the determinant can be used, because the determinant is the product of the eigenvalues. If it is positive, then the eigenvalues are both positive, or both negative. If it is negative, then the two eigenvalues have different signs. If it is zero, then the second-derivative test is inconclusive.

Equivalently, the second-order conditions that are sufficient for a local minimum or maximum can be expressed in terms of the sequence of principal (upper-leftmost) minors (determinants of sub-matrices) of the Hessian; these conditions are a special case of those given in the next section for bordered Hessians for constrained optimization—the case in which the number of constraints is zero. Specifically, the sufficient condition for a minimum is that all of these principal minors be positive, while the sufficient condition for a maximum is that the minors alternate in sign, with the minor being negative.

Critical points[edit]

If the gradient (the vector of the partial derivatives) of a function is zero at some point then has a critical point (or stationary point) at The determinant of the Hessian at is called, in some contexts, a discriminant. If this determinant is zero then is called a degenerate critical point of or a non-Morse critical point of Otherwise it is non-degenerate, and called a Morse critical point of

The Hessian matrix plays an important role in Morse theory and catastrophe theory, because its kernel and eigenvalues allow classification of the critical points.^[2][3][4]

The determinant of the Hessian matrix, when evaluated at a critical point of a function, is equal to the Gaussian curvature of the function considered as a manifold. The eigenvalues of the Hessian at that point are the principal curvatures of the function, and the eigenvectors are the principal directions of curvature. (See Gaussian curvature § Relation to principal curvatures.)

Use in optimization[edit]

Hessian matrices are used in large-scale optimization problems within Newton-type methods because they are the coefficient of the quadratic term of a local Taylor expansion of a function. That is,

where is the gradient Computing and storing the full Hessian matrix takes memory, which is infeasible for high-dimensional functions such as the loss functions of neural nets, conditional random fields, and other statistical models with large numbers of parameters. For such situations, truncated-Newton and quasi-Newton algorithms have been developed. The latter family of algorithms use approximations to the Hessian; one of the most popular quasi-Newton algorithms is BFGS.^[5]

Such approximations may use the fact that an optimization algorithm uses the Hessian only as a linear operator and proceed by first noticing that the Hessian also appears in the local expansion of the gradient:

Letting for some scalar this gives

that is,

so if the gradient is already computed, the approximate Hessian can be computed by a linear (in the size of the gradient) number of scalar operations. (While simple to program, this approximation scheme is not numerically stable since has to be made small to prevent error due to the term, but decreasing it loses precision in the first term.^[6])

Notably regarding Randomized Search Heuristics, the evolution strategy’s covariance matrix adapts to the inverse of the Hessian matrix, up to a scalar factor and small random fluctuations.
This result has been formally proven for a single-parent strategy and a static model, as the population size increases, relying on the quadratic approximation.^[7]

Other applications[edit]

The Hessian matrix is commonly used for expressing image processing operators in image processing and computer vision (see the Laplacian of Gaussian (LoG) blob detector, the determinant of Hessian (DoH) blob detector and scale space). It can be used in normal mode analysis to calculate the different molecular frequencies in infrared spectroscopy.^[8] It can also be used in local sensitivity and statistical diagnostics.^[9]

Generalizations[edit]

Bordered Hessian[edit]

A bordered Hessian is used for the second-derivative test in certain constrained optimization problems. Given the function considered previously, but adding a constraint function such that the bordered Hessian is the Hessian of the Lagrange function ^[10]

If there are, say, constraints then the zero in the upper-left corner is an block of zeros, and there are border rows at the top and border columns at the left.

The above rules stating that extrema are characterized (among critical points with a non-singular Hessian) by a positive-definite or negative-definite Hessian cannot apply here since a bordered Hessian can neither be negative-definite nor positive-definite, as if is any vector whose sole non-zero entry is its first.

The second derivative test consists here of sign restrictions of the determinants of a certain set of submatrices of the bordered Hessian.^[11] Intuitively, the constraints can be thought of as reducing the problem to one with free variables. (For example, the maximization of subject to the constraint can be reduced to the maximization of without constraint.)

Specifically, sign conditions are imposed on the sequence of leading principal minors (determinants of upper-left-justified sub-matrices) of the bordered Hessian, for which the first leading principal minors are neglected, the smallest minor consisting of the truncated first rows and columns, the next consisting of the truncated first rows and columns, and so on, with the last being the entire bordered Hessian; if is larger than then the smallest leading principal minor is the Hessian itself.^[12] There are thus minors to consider, each evaluated at the specific point being considered as a candidate maximum or minimum. A sufficient condition for a local maximum is that these minors alternate in sign with the smallest one having the sign of A sufficient condition for a local minimum is that all of these minors have the sign of (In the unconstrained case of these conditions coincide with the conditions for the unbordered Hessian to be negative definite or positive definite respectively).

Vector-valued functions[edit]

If is instead a vector field that is,

then the collection of second partial derivatives is not a matrix, but rather a third-order tensor. This can be thought of as an array of Hessian matrices, one for each component of :

This tensor degenerates to the usual Hessian matrix when

Generalization to the complex case[edit]

In the context of several complex variables, the Hessian may be generalized. Suppose and write Then the generalized Hessian is If satisfies the n-dimensional Cauchy–Riemann conditions, then the complex Hessian matrix is identically zero.

Generalizations to Riemannian manifolds[edit]

Let be a Riemannian manifold and its Levi-Civita connection. Let be a smooth function. Define the Hessian tensor by

where this takes advantage of the fact that the first covariant derivative of a function is the same as its ordinary differential. Choosing local coordinates gives a local expression for the Hessian as

where are the Christoffel symbols of the connection. Other equivalent forms for the Hessian are given by

See also[edit]

• The determinant of the Hessian matrix is a covariant; see Invariant of a binary form
• Polarization identity, useful for rapid calculations involving Hessians.
• Jacobian matrix – Matrix of all first-order partial derivatives of a vector-valued function
• Hessian equation

Notes[edit]

Further reading[edit]

• Lewis, David W. (1991). Matrix Theory. Singapore: World Scientific. ISBN 978-981-02-0689-5.
• Magnus, Jan R.; Neudecker, Heinz (1999). «The Second Differential». Matrix Differential Calculus : With Applications in Statistics and Econometrics (Revised ed.). New York: Wiley. pp. 99–115. ISBN 0-471-98633-X.

External links[edit]

• «Hessian of a function», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. «Hessian». MathWorld.

Применение поверхностей первого и второго порядков
в задачах на экстремум функций

Общая постановка задачи поиска экстремума функций приведена здесь. Рассмотрим задачу поиска безусловного экстремума функций двух переменных.

Аналитический метод поиска локального безусловного экстремума

Пусть задана дважды непрерывно дифференцируемая функция двух переменных.

Точка называется точкой локального минимума, если существует такая окрестность этой точки, для всех точек которой выполняется условие

Если знак неравенства заменить на знак , то получится определение локального максимума. Точки локального минимума или максимума называются точками локального экстремума функции.

Требуется найти точки локального экстремума функции .

Порядок решения поставленной задачи содержит два этапа.

На первом этапе при помощи необходимых условий экстремума первого порядка:

находятся стационарные точки , «подозрительные» на наличие локального экстремума (частные производные первого порядка в точке равны нулю).

На втором этапе проверяются достаточные условия экстремума, а если они не выполняются, то и необходимые условия второго порядка. Они следуют из формулы Тейлора для приращения функции в точке (учитывая члены до второго порядка включительно):

где

а члены с производными первого порядка отсутствуют, так как точка удовлетворяет (4.74).

Равенство

можно рассматривать как уравнение поверхности второго порядка относительно неизвестных . Уравнение (4.75) можно записать в матричной форме

где — матрица квадратичной формы, называемая матрицей Гессе.

Она составлена из частных производных второго порядка, вычисленных в стационарной точке

Как показано в разд.4.4.1, при помощи поворота системы координат вокруг оси можно квадратичную форму в правой части (4.76) привести к каноническому виду

где — собственные значения матрицы Гессе .

В зависимости от знаков собственных значений возможны следующие случаи:

1) если собственные значения одного знака, то поверхность (4.77) представляет собой эллиптический параболоид: выпуклый при (рис.4.58,а), или вогнутый при (рис.4.58,б);

2) если собственные значения имеют разные знаки, то поверхность (4.77) представляет собой гиперболический параболоид (рис.4.58,в при );

3) если одно из собственных значений равно нулю (например, при ), то поверхность (4.77) представляет собой параболический цилиндр: выпуклый при (рис.4.58,2) или вогнутый при (рис.4.58,д).

В случае эллиптического параболоида стационарная точка является либо точкой локального минимума функции при , либо точкой локального максимума функции при . В случае гиперболического параболоида ( и имеют разные знаки) в стационарной точке нет экстремума. В случае выпуклого параболического цилиндра можно сказать, что точка не может быть точкой максимума, но может быть точкой минимума, в случае вогнутого параболического цилиндра точка не может быть точкой минимума, но может быть точкой максимума. Таким образом, если хотя бы одно собственное значение равно нулю, судить о наличии экстремума в точке нельзя, так как нужны дополнительные исследования, учитывающие в формуле Тейлора члены выше второго порядка.

Алгоритм исследования функции на локальный экстремум

1. Составить и решить систему (4.74) — найти стационарные точки . Если система не имеет решения, то точек локального экстремума нет.

2. Составить матрицу Гессе и найти ее собственные значения и , решая характеристическое уравнение

3. Проверить выполнение следующих условий.

а) Если , то — точка локального минимума.

б) Если , то — точка локального максимума.

в) Если , то может быть точкой локального минимума (требуется дополнительное исследование).

г) Если , то может быть точкой локального максимума (требуется дополнительное исследование).

д) Если и разных знаков , то не является точкой локального экстремума.

Пример 4.25. Найти экстремумы функции .

Решение.. Решая систему уравнений

находим стационарные точки и .

Составляем матрицу Гессе .

В стационарной точке матрица Гессе . Найдем собственные значения матрицы Гессе. Характеристическое уравнение

имеет корни разных знаков. Следовательно, точка не является точкой экстремума (см. п.3,»д» алгоритма).

В стационарной точке матрица Гессе . Характеристическое уравнение

имеет два положительных корня . Следовательно, точка является точкой минимума (см. п.3,»а» алгоритма).

Применение графических методов поиска экстремума функции

Рассмотрим постановку задачи поиска условного экстремума функции трех переменных. Пусть заданы:

а) функция трех переменных ;

б) множество допустимых решений .

Требуется найти такую точку из множества допустимых решений, которой соответствует минимальное значение функции на этом множестве:

Алгоритм графического метода поиска условного (или безусловного экстремума) функции аналогичен алгоритму, рассмотренному ранее для функции двух переменных. Однако его применение на практике ограничивается возможностями изображения пространственных фигур. Как правило, используется плоское изображение пространственных фигур, т.е. проекции этих фигур на плоскость, что не дает полного представления о взаимном их расположении.

Ниже рассматриваются задачи, в которых минимизируемая функция и функции, задающие ограничения, являются многочленами трех переменных первой или второй степени. Построение множества допустимых решений и поверхностей уровня функции сводится к построению алгебраических поверхностей первого или второго порядков. В этих задачах применение графического метода упрощается.

Напомним, что поверхностью уровня функции называется геометрическое место точек пространства, в которых функция принимает постоянное значение, т.е. .

Если функция является многочленом первой степени, то ее поверхности уровня при разных значениях постоянной представляют собой семейство параллельных плоскостей (несобственный пучок плоскостей).

Если функция является многочленом второй степени, то ее поверхности уровня при разных значениях постоянной представляют собой поверхности второго порядка. Поскольку уравнения разных поверхностей уровня отличаются только свободными членами, то собственные векторы, собственные значения , а также инварианты остаются постоянными для всех поверхностей уровня . Следовательно, тип поверхности и канонический базис остаются постоянными для всех поверхностей уровня квадратичной функции.

Пример 4.26. Графическим методом найти экстремумы:

Решение.

1) 1. Множество допустимых решений строить не нужно, так как оно совпадает со всем пространством: .

2. Поверхность уровня при представляет собой эллипсоид (рис.4.59,а), при — мнимый конус с единственной вещественной точкой , при — мнимый эллипсоид. При увеличении постоянной полуоси эллипсоида пропорционально увеличиваются. На рис.4.59,а изображены эллипсоиды

и

Стрелками указаны направления наискорейшего возрастания функции.

3. Из пункта 2 следует, что допустимые значения функции определяются не равенством .

4. В точке достигается безусловный минимум функции, так как в этой точке функция принимает наименьшее значение по сравнению со значениями в других точках пространства, а наибольшего значения функция не достигает.

2) Решается задача поиска условного экстремума с ограничениями типа равенств и неравенств.

1. Строим множество допустимых решений — часть плоскости в первом октанте, т.е. плоский треугольник с вершинами (рис.4.59,б).

2. Поверхности уровня функции представляют собой семейство параллельных плоскостей, каждая из которых перпендикулярна оси аппликат. На рис.4.59,б изображены три плоскости уровня . При или плоскость не имеет общих точек с треугольником ; при плоскость имеет общие точки с треугольником , в частности, при плоскости принадлежит сторона треугольника, при плоскости принадлежит вершина треугольника.

3. Из пункта 2 следует, что допустимые значения функции определяются неравенством .

4. Наименьшее значение на множестве , равное нулю, функция достигает в любой точке отрезка ; наибольшее значение на множестве , равное единице, функция достигает в точке .

3) Решается задача поиска условного экстремума с ограничением типа равенств.

1. Строим множество допустимых решений — сфера единичного радиуса с центром в начале координат (рис.4.60).

2. Поверхности уровня представляют собой либо однополостный гиперболоид вращения при (например, однополостный гиперболоид (рис.4.60,а)), либо круговой конус при (рис.4.60,б), либо двуполостный гиперболоид вращения при (например, двуполостный гиперболоид (рис.4.60,в)). При поперечные полуоси однополостного гиперболоида больше единицы, и он не имеет общих точек со сферой единичного радиуса. При продольная полуось двуполостного гиперболоида больше единицы, и он не имеет общих точек со сферой . При поверхность уровня имеет общие точки с заданной сферой.

3. Из п.2 следует, что допустимые значения функции определяются неравенством .

4. Наименьшее значение на множестве , равное –1, функция достигает в точках — вершинах двуполостного гиперболоида (рис.4.60,в); наибольшее значение на множестве , равное единице, функция достигает в точках окружности т.е. в точках горлового эллипса (в данном случае окружности) однополостного гиперболоида вращения (рис.4.60,а).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.