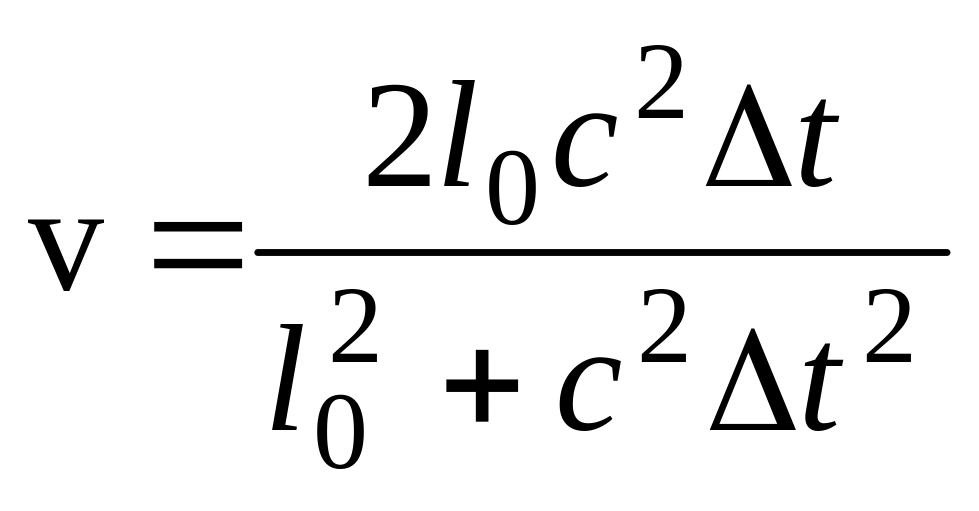2018-03-24
Найти собственную длину стержня, если в лабораторной системе отсчета его скорость $v = c/2$, длина $l = 1,00 м$ и угол между ним и направлением движения $theta = 45^{ circ}$.
Решение:
В покоящийся системе отсчета координаты концов стержня в определениях собственной длины $l_{0}$
$A: (0,0,0) B: (l_{0} cos theta_{0}, l_{0} sin theta_{0},0)$
в момент времени $t$. В лабораторной системе отсчета координаты в момент времени $t^{ prime}$
$A: (vt^{ prime}, 0,0), B: left ( l_{0} cos theta_{0} sqrt{1 — beta^{2} } + vt^{ prime}, l_{0} sin theta_{0}, 0 right )$
Поэтому мы можем написать,
$l cos theta_{0} = l_{0} cos theta_{0} sqrt{ 1 — beta^{2} }$ и $l sin theta = l_{0} sin theta_{0}$
следовательно $l_{0}^{2} = l^{2} left ( frac{ cos^{2} theta + (1 — beta^{2} ) sin^{2} theta }{1 — beta^{2} } right )$
или, $ = sqrt{ frac{ 1 — beta^{2} sin^{2} theta }{1 — beta^{2} } }$
2.2.3. Собственная длина и собственный объем[править]
Рассмотрим стержень, который покоится в системе отсчета К и параллельный оси «х». Длина стержня в системе К может быть вычислена:

Найдем длину этого стержня в системе отсчета K’, которая движется относительно К с постоянной скоростью V.

По определению, «собственной длиной» стержня называется его длина в той системе, в которой стержень покоится.
Обозначим собственную длину неподвижного стержня 


Как видно, самую большую длину стержень имеет в той системе отсчета, в которой он покоится. При движении длина уменьшается, этот эффект называют «Лоренцевым сокращением».
Из выражений (2.2.11) легко показать, что поперечные размеры тела не изменяются при движении вдоль оси «х». Это означает, что объем тела меняется точно так же, как и его длина:

где V0 — это «собственный объем» тела.
См. также[править]
<<Назад | Далее>>
Оглавление
Примечания[править]
Примеры решения задач
Пример 1.
Найти собственную длину стержня
,
если в
—
системе отсчета его скорость
,
длина
м
и угол между ним и направлением движения
.
Р е ш е н и е.
Лоренцевскому сокращению подвергаются
только размеры тела в направлении
движения (оси
и
в
и
системах).
Поперечные размеры тела вдоль осей
—
и
—
в
—
и
—
системах отсчета не претерпевают
Лоренцевского сокращения длины. Пусть
Тогда
С учетом записанных
формул можно получить
,
Исключая из этих
двух уравнений угол
с помощью соотношения
имеем
Окончательно
м
Пример 2.
С какой скоростью двигались в
системе
отсчета часы, если за время
=5с
(в
системе)
они отстали от часов этой системы на
с?
Р е ш е н и е. Пусть
времени
в
системе
соответствует собственное время
в
системе. Согласно преобразованиям
Лоренца
.
По условию задачи
.
Откуда имеем
или
После несложных
преобразований находим
Пример 3. Два
стержня одинаковой собственной длины
движутся навстречу друг к другу
параллельно общей горизонтальной оси.
В системе отсчета, связанной с одним из
стержней, промежуток времени между
моментами совпадения левых и правых
концов стержней оказался равным
.
Какова скорость одного стержня
относительно другого?
Р е ш е н и е. Свяжем
с одним из стержней, который будем
условно считать неподвижным,
систему,
а со вторым движущимся стержнем
систему
отсчтета. Благодаря эффекту Лоренцевского
сокращения длина второго стержня
в
системе
будет
Если этот стержень
пролетает мимо первого стержня слева
направо, и в некоторый момент времени
его левый конец совпадает с левым концом
первого стержня (неподвижного в
системе),
то в этот момент правый конец второго
стержня еще не будет совмещен с правым
концом первого стержня, поскольку ему
надо еще пройти расстояние (
со
скоростью
.
Тогда
.
Исключая из
записанных соотношений величину
,
получим
.
После возведения
в квадрат и сокращения
в левой и правой части найдем
.
Пример
4. Рассмотрим
задачу, сформулированную в вопросе 5 из
«Вопросов для самоконтроля».
Р е ш е н и е. В К-СО
, относительно которой частицы двигаются
со скоростью v,
расстояние между ними равно
.
В этой системе отсчета это расстояние
испытало Лоренцево сокращение длины.
Поэтому согласно формуле (2)
Релятивистская динамика
Нерелятивистское
определение импульса
оказывается неадекватным в СТО. Во
многих случаях в задачах нерелятивистской
динамики при таком определении импульса
оказывается несправедливым закон
сохранения импульса (ЗСИ). В то же время
ЗСИ отражает такое важное свойство
окружающего нас пространства как
однородность (механические свойства
окружающего нас пространства не меняются
при любом параллельном переносе системы
как целого в пространстве). В теоретической
физике показывается, что ЗСИ будет
выполняться и в релятивистской динамике,
если в качестве импульса использовать
определение
(5)
Релятивистское
выражение второго закона Ньютона при
этом имеет вид
(6)
Если для ускорения
принять обычное определение
и выполнить дифференцирование в правой
части (6), то можно получить уравнение
(7)
где
.
Из формулы (7) можно
понять, что при скоростях, близких к
скорости света, масса уже не является
мерой инертности тела, как в классической
механике, где
Ускорение тела уже не будет в общем
случае совпадать по направлению с силой.
Наряду с вектором, направленным вдоль
вектора ускорения
в правой части релятивистского уравнения
движения (5) в общем случае появляется
слагаемое ~
которое отсутствует в классическом
уравнении
Для энергии
свободной частицы массы
,
движущейся со скоростью
в СТО получается выражение
(8)
откуда видно, что
в отличие от классической механики
энергия свободной частицы не обращается
в нуль при
а равна
Величина
носит название энергии покоя. Формулы
(5) ÷ (8) справедливы и для составных тел,
состоящих из многих частиц. Под
следует понимать полную массу тела,
которая определяется соотношением
,
(9)
где
и
–
энергия и импульс тела как целого.
Величина
связана со скоростью
движения тела как целого соотношением
(10)
Из формул (9) и (10)
легко получить (5) и (8), однако в случае
частиц с массой равной нулю (фотоны)
соотношения (9) и (10) более удобны, поскольку
они не содержат неопределенностей
(при
обращается
в нуль выражение
).
В то же время из формулы (10) для фотона
имеем
,
а из соотношения (9) при этом получим
.
Энергия покоящегося составного тела
содержит в себе помимо энергии покоя
входящих в его состав частиц, также
кинетическую энергию частиц и энергию
их взаимодействия. Это приводит к такому
нетривиальному свойству релятивистской
массы как ее неаддитивность: масса
составного тела не равна сумме масс
составляющих его частиц. Разность
носит название дефекта масс, а само
существование этой разности лежит в
основе всей энергетики, причем не только
ядерной, но и самой традиционной:
например, при обычной реакции сгорания
дефект массы исходного топлива и
продуктов сгорания выделяется в виде
тепловой энергии. Согласно формуле (9)
в релятивистской динамике имеет место
закон сохранения массы: масса замкнутой
системы остается постоянной при всех
процессах, которые происходят в системе.
Это объясняется тем, что в замкнутой
системе сохраняется энергия
и величина импульса
,
а значит сохраняется и комбинация
Можно показать, что масса
является релятивистским инвариантом,
наряду со скоростью света
и интервалом
Интересно, что энергия
и импульс
не будучи сами релятивистскими
инвариантными величинами вместе образуют
4-х вектор
который образует комбинацию
которая является релятивистским
инвариантом.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Заголовок сообщения: Собственная длина стержня
Добавлено: 13 ноя 2014, 15:59
|
Зарегистрирован: 22 ноя 2013, 10:03
Сообщений: 71
Определить собственную длину стержня, если в лабораторной системе его скорость `v=0.6`c, а длина `l=0.5`м и угол между ним и направлением движения `alpha=30`
Ответ: 1,79 м.
Куда засунуть этот угол? Понятия не имею. По формуле `l=l_0sqrt(1-(v^2)/c^2)` выразить `l_0` а дальше с углом как?


vyv2
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 18:01
Зарегистрирован: 31 янв 2011, 17:37
Сообщений: 4974
Откуда: Санкт-Петербург
DiSE писал(а):
Определить собственную длину стержня, если в лабораторной системе его скорость `v=0.6`c, а длина `l=0.5`м и угол между ним и направлением движения `alpha=30`
Ответ: 1,79 м.
Куда засунуть этот угол? Понятия не имею. По формуле `l=l_0sqrt(1-(v^2)/c^2)` выразить `l_0` а дальше с углом как?
Надо учесть, что длина изменяется по направлению движения (т.е. изменяется один из катетов) и не изменяется перпендикулярно движению.
Но на мой взгляд скорость слишком мала, чтобы так сильно по ответу изменилась собственная длина стержня.
Откуда задачка?
_________________
Сопротивление бесполезно.
Последний раз редактировалось vyv2 13 ноя 2014, 18:16, всего редактировалось 1 раз.


DiSE
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 18:06
|
Зарегистрирован: 22 ноя 2013, 10:03
Сообщений: 71
Задача со сборника УГАТУ, Трофимовой.
Ничего не могу придумать. Тут если брать по треугольникам, то ничего у меня не выходит.


vyv2
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 18:17
Зарегистрирован: 31 янв 2011, 17:37
Сообщений: 4974
Откуда: Санкт-Петербург
DiSE писал(а):
Задача со сборника УГАТУ, Трофимовой.
Ничего не могу придумать. Тут если брать по треугольникам, то ничего у меня не выходит.
См. предыдущее замечание
_________________
Сопротивление бесполезно.


DiSE
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 18:33
|
Зарегистрирован: 22 ноя 2013, 10:03
Сообщений: 71
Цитата:
Надо учесть, что длина изменяется по направлению движения (т.е. изменяется один из катетов) и не изменяется перпендикулярно движению.
Нет, все равно не понял что вы говорите


vyv2
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 18:51
Зарегистрирован: 31 янв 2011, 17:37
Сообщений: 4974
Откуда: Санкт-Петербург
DiSE писал(а):
Цитата:
Надо учесть, что длина изменяется по направлению движения (т.е. изменяется один из катетов) и не изменяется перпендикулярно движению.
Нет, все равно не понял что вы говорите
Похожая задача:
Вложение:
1a.JPG [ 51.58 KIB | Просмотров: 8299 ]
_________________
Сопротивление бесполезно.


DiSE
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 19:01
|
Зарегистрирован: 22 ноя 2013, 10:03
Сообщений: 71
Спасибо. Здесь все таки не опечатка в условие. Я думал что скорость в секундах тут измеряется, а тут оказывается 0,6с, где с- скорость света


vyv2
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 19:17
Зарегистрирован: 31 янв 2011, 17:37
Сообщений: 4974
Откуда: Санкт-Петербург
DiSE писал(а):
Спасибо. Здесь все таки не опечатка в условие. Я думал что скорость в секундах тут измеряется, а тут оказывается 0,6с, где с- скорость света
Никогда не подозревал, что скорость может измеряться в секундах.
_________________
Сопротивление бесполезно.


DiSE
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 19:36
|
Зарегистрирован: 22 ноя 2013, 10:03
Сообщений: 71


vyv2
Заголовок сообщения: Re: Собственная длина стержня
Добавлено: 13 ноя 2014, 19:45
Зарегистрирован: 31 янв 2011, 17:37
Сообщений: 4974
Откуда: Санкт-Петербург
С ответом сошлось?
_________________
Сопротивление бесполезно.


поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.