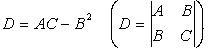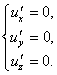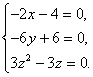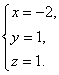Как найти смешанную производную двух переменных - AvtoShod.ru

Заказать задачи по любым предметам можно здесь от 10 минут

Смешанная частная производная

Как найти?

Постановка задачи

Найти смешанную частную производную второго порядка функции $ z = f(x_1,x_2) $

План решения

Смешанная частная производная второго порядка функции $ z = f(x_1,x_2) $ по переменным $ x_1 $ и $ x_2 $ обозначается: $ frac{partial^2 z}{partial x_1 partial x_2} $ или $ z»_{x_1 x_2} $

Порядок дифференцирования не имеет значения, то есть выполняется свойство:

$$ frac{partial^2 z}{partial x_1 partial x_2} = frac{partial^2 z}{partial x_1 partial x_2} $$

$$ z»_{xy} = z»_{yx} $$

Фиксируем $ x_2 $. Считая функцию $ z = f(x_1,x_2) $ одной переменной от $ x_1 $ находим её производную $ z’_{x_1} $
Фиксируем $ x_1 $ и по правилу дифференцирования функции одной переменной находим производную функции $ z = f(x_1,x_2) $ по $ x_2 $ и получаем $ z»_{x_1 x_2} $

Примеры решений

Пример 1

Найти смешанную частную производную функции $ z(x,y) = ln (x+y) $

Решение

Фиксируем переменную $ x $ и находим производную по $ y $:

$$ z’_y = frac{1}{x+y} cdot (x+y)’_y = frac{1}{x+y} $$

Считая переменную $ y $ постоянной дифференцируем функцию $ z’_y $ по $ x $:

$$ z»_{yx} = -frac{1}{(x+y)^2} cdot (x+y)’_x = -frac{1}{(x+y)^2} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z»_{xy} = z»_{yx} = -frac{1}{(x+y)^2} $$

Пример 2

Найти смешанную производную функции $ z(x,y) = sin x cos y $

Решение

Фиксируем переменную $ y $ и выполняем дифференцирование по $ x $:

$$ z’_x (y = const) = cos x cos y $$

Считаем постоянной $ x $ и находим производную по $ y $:

$$ z’_{xy} (x = const) = -cos x sin y $$

Ответ

$$ z’_{xy} = z’_{yx} = -cos x sin y $$

Источник

Смешанная производная

Содержание:

Теорема 10.4 (о равенстве смешанных производных):
Доказательство:

Пусть функция определена и имеет частные производные и во всех точках множества . Тогда и сами являются функциями двух переменных, и, стало быть, можно определить их частные производные:

Они называются частными производными второго порядка функции .

Точно таким же образом можно определить частные производные -го порядка для произвольного натурального . Они называются частными производными высших порядков. — примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка и , которые называются смешанными производными?

Ответ на этот вопрос в общем случае отрицательный. Однако справедлива следующая теорема.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 10.4 (о равенстве смешанных производных):

Пусть функция и ее частные производные

определены в некоторой окрестности точки , причем и непрерывны в точке . Тогда в точке .

Доказательство:

Составим смешанные частные приращения функции :

(109)

Учитывая последнее равенство и применяя теорему Лагранжа по переменной к функции на промежутке , получим , (10.10)

где .

Применение теоремы Лагранжа правомерно, поскольку по предположению теоремы существует частная производная в достаточно малой окрестности точки . Так как такое же предположение верно и для частной смешанной производной то, снова применяя теорему Лагранжа на промежутке , из (10.10) получим , (10.11) где . Поскольку по условию теоремы функция непрерывна в точке , то последнее равенство можно записать в следующей форме: , (10.12) где при и . Из (10.12) следует, что . (10.13) Совершенно аналогично можно доказать, что

. (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.

Возможно вам будут полезны данные страницы:

Замечание 10.2.

В последней теореме условие непрерывности смешанных производных является существенным. То есть при отсутствии этого условия смешанные производные могут быть различными в данной точке .

Действительно, рассмотрим функцию и докажем, что ее смешанные частные производные в точке (0,0) не равны друг другу. Действительно,

Теперь вычислим вторые производные: Осталось заметить, что смешанные частные производные разрывны в точке (0,0). В самом деле, например, при . Следовательно, . А это значит, что не является непрерывной в точке (0,0).

Лекции:

Предел функции
Знакочередующиеся ряды
Производная неявной функции
Неопределенный интеграл
Формула Байеса
Значения случайной величины
Площади поверхностей круглых фигур
Интегралы для чайников
Метод координат на прямой и его применение
Системы счисления

Источник

Теорема 1(для функции двух переменных)

Пусть
функция f(x,y) определенна
со своими частными производными fx,fy,fxy,fyx в
некоторой окрестности точки (x0,y0),
и при этом fxy и
fyx
непрерывны
в этой точке. Тогда эти производные
равны ( результат не зависит от порядка
дифференцирования).

fxy(x0,y0)=fyx(x0,y0)

Теорема 2(обобщение)

Если у
функции n переменных
смешанные частные производные m-го
порядка непрерывны в некоторой точке,
а производные низших порядков непрерывны
в окрестности этой точки, то частные
производные порядка m не
зависят от порядка дифференцирования.

<Вернуться
назад>

27. Дифференцируемость функции нескольких переменных. Дифференциал.

Обозначения:
или –
частная производная по «икс»
или –
частная производная по «игрек»

Полный дифференциал
первого порядка функции
двух переменных имеет вид:

И по неоднократным
просьбам читателей, полный
дифференциал второго порядка:

Пусть
функция дифференцируема
в точке ,
то есть приращение этой функции можно
представить в виде суммы двух слагаемых:
линейного относительно и
нелинейного членов:

где при .

Определение

Дифференциалом
функции называется
линейная относительно часть
приращения функции. Она обозначается
как или .
Таким образом:

Замечание

Дифференциал
функции составляет основную часть ее
приращения.

Замечание

Наряду
с понятием дифференциала функции
вводится понятие дифференциала аргумента.
По определению дифференциал
аргумента есть приращение
аргумента:

Замечание

Формулу
для дифференциала функции можно записать
в виде:

Отсюда
получаем, что

Итак,
это означает, что производная может
быть представлена как обыкновенная
дробь — отношение дифференциалов функции
и аргумента.

Геометрический смысл дифференциала

Дифференциал
функции в точке равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента .

<Вернуться
назад>

28. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума.

Локальный
экстремум функции двух
переменных

Необходимое
условие локального экстремума
дифференцируемой функции

Если —
точка экстремума функции f,
то

и или

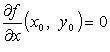
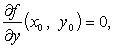
Достаточные
условия локального экстремума дважды
дифференцируемой функции

Обозначим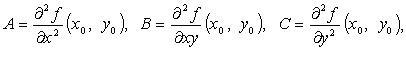

(Также принято
обозначать: D-M_1,2,3;
A,B,C
– Uxx_,Uxy,
…)

Если
D > 0, A > 0, то —
точка минимума.

Если
D > 0, A < 0, то —
точка максимума.

Если
D < 0, экстремума в точке нет.

Если
D = 0, необходимы дополнительные
исследования.

Пример
от 3х переменных:

Решение
Найдем
стационарные точки заданной функции,
то есть точки, в которых выполняется
необходимое условие существования
экстремума. Для функции трех
переменных стационарные
точки (координаты точек) находятся из
системы
Для
заданной функции , ,

и
система примет вид
Решениями
системы являются 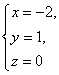 и
Получили
две стационарные точки  и .
Для
проверки достаточных условий экстремума
в стационарной точке необходимо
определить знаки определителей ,
и  в
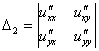
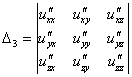
этой точке.
Найдем , , , , , .
Для
точки  ,

,
.

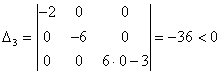
Так
как , , ,
то в точке функция
имеет максимум, при этом
.
Для
точки ,

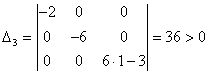
Так
как , , ,
то в точке функция
не имеет экстремума.

<Вернуться
назад>

Справка

1. Q:
Как перейти по
ссылке на определенный вопрос?

A: Нажать на ссылку, потом
— на появившуюся ссылку под ней:

Или “ctrl
+ ЛКМ”.

2.
Q: Как добавить
закладку?

A:
Выделить фрагмент текста, на который
будет сделана закладка, нажать в верхнем
меню “Вставка” ->
“Закладка”

3.
Q: Как добавить
ссылку на закладку?

A: Выделить текст будущей
ссылки, нажать сочетание “ctrl + K”,
кликнуть в появившеся меню “Закладки
>” и выбрать нужную закладку.

4.
Q: Как вставить разделитель после
вопроса, чтобы следующий всегда был на
новой странице?

A:
Нажать
ctrl + Enter

Спасибо!

Всем,
кто писал ответы на вопросы:

Линар Саитов
Арсений Автомонов
Хитров Николай

<Вернуться
назад>

By IKBO-08-16
&
IKBO-13-17

2016-2018

©mirea

Соседние файлы в папке 1-й семестр

Источник

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.

Частные производные функции z(x,y) находятся по следующим формулам:

Вторые частные производные функции z(x,y) находятся по формулам:

Смешанные частные производные функции z(x,y) находятся по формулам:

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.

Решение онлайн
Видеоинструкция
Также решают

Правила ввода функции, заданной в явном виде

Примеры

x²+xy ≡ x^2+x*y.

cos²(2x+y) ≡ (cos(2*x+y))^2

≡ (x-y)^(2/3)

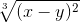
Правила ввода функции, заданной в неявном виде

Все переменные выражаются через x,y,z

Примеры

≡ x^2/(z+y)

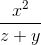
cos²(2x+zy) ≡ (cos(2*x+z*y))^2

≡ z+(x-y)^(2/3)

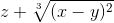
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δ_xz=f(x+Δ_x,y)-f(x,y) – это частное приращение функции z по аргументу x; Δ_yz=f(x,y+Δ_y)-f(x,y) – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

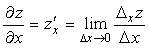
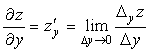
– это частная производная функции z по аргументу x;

– это частная производная функции z по аргументу у.

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x⁵+3x²y+y²–4x+5y-1

Пример 2. Найти частные производные функции z = f(x;y) в точке A(x₀;y₀).

Находим частные производные:

Найдем частные производные в точке А(1;1)

Находим вторые частные производные:

Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

I Основные понятия функции нескольких
переменных

1.1 Понятие функции нескольких переменных

Пусть D – некоторое множество пар
действительных чисел и пусть каждой паре (x; y)
из D поставлено в соответствие число Z.
Тогда говорят, что на множестве D задана функция
двух переменных Z = f(x,y).

Переменные x,y называют независимыми
переменными (или аргументами), Z —
зависимой переменной; говорят также, что f(x,y)
есть значение функции f в точке (x;y).

Множество D называют областью
определения функции.

Все значения, которые принимает функция f(x,y)
(при (x,y) принадлежащих области её
определения), образуют область значений
функции.

Аналогично можно ввести понятие функции трех
переменных u = f(x,y,z), определенной на множестве
D, состоящем не из действительных чисел (как
для функции одной переменной) и не из пар
действительных чисел (как для функции двух
переменных), а из троек действительных чисел (x,y,z),
рассматриваемых в определенном порядке. Можно
ввести понятие функции четырех, пяти и вообще
любого конечного числа переменных – все такие
функции называют функциями нескольких
переменных.

Примеры функций нескольких переменных:

S = xy – площадь прямоугольника со сторонами x, y
есть функция двух переменных;

U = IR (закон Ома) – напряжение U на участке
электрической цепи есть функция двух переменных:
силы тока I и сопротивления R;

V = xyz — объем прямоугольного параллелепипеда со
сторонами x,y,z есть функция трех переменных.

Чтобы задать функцию двух (трех) переменных,
нужно указать способ, с помощью которого для
каждой пары (тройки) значений аргументов можно
найти соответствующее значение функции.

Наиболее употребительным (как и в случае
функций одной переменной) является способ
задания функции с помощью формулы Z = f(x,y), где
f(x,y) – некоторое выражение с переменными x,y.
В таком случае говорят, что функция задана
формулой или что функция задана аналитически.

Значение функции Z = f(x,y) в точке M(x₀,y₀)
называется частным значением функции и
обозначается f(x₀,y₀) или f(M).

Пример:

Дана функция Вычислить

1.2 Область определения

Область определения функции Z = f(x,y)в
простейших случаях представляет собой либо
часть плоскости, ограниченную замкнутой кривой,
причем точки этой кривой (границы области) могут
принадлежать или не принадлежать области
определения, либо всю плоскость, либо, наконец,
совокупность нескольких частей плоскости xOy

Геометрическим изображением функции Z = f(x,y)
в прямоугольной системе координат Oxyz
(графиком функции) является некоторая плоскость.

Для аналитически заданной функции иногда не
указывают явно область ее определения. В таком
случае подразумевают, что область определения
функции Z = f(x,y) совпадает с областью
определения выражения Z = f(x,y), т.е. с
множеством тех значений x,y, при которых
выражение f(x,y) имеет смысл.

Пример: Найти область определения функции:

а) Функция не определена лишь в случае, когда y =
x. Геометрически это означает, что область
определения функции состоит из двух
полуплоскостей, одна из которых лежит выше, а
другая ниже прямой y = x.

б) Функция определена при условии ,
т.е. . Это круг с центром в начале координат и
радиусом , включающий свою границу, т.е. окружность =
1.

в) Функция определена при условии —
4 > 0, т.е. > 4. Это часть плоскости, лежащая
вне круга с центром в начале координат и радиусом
2, не включающая границу круга, т.е. окружность =
4

г) Функция определена при (x,y,z),
удовлетворяющих одновременно условиям x
0, y 0, z 0.

1.3 Частные производные

Пусть задана функция Z = f(x,y).

Переменной x дадим приращение dx, а y оставим без
изменения. Если существует предел:

то он называется частной производной от
функции Z = f(x,y) по переменной x.

Обозначать частную производную от функции Z =
f(x,y) по переменной x можно любым из
символов:

Чтобы найти частную производную от функции Z =
f(x,y) по переменной x, нужно найти
производную от этой функции по x, считая,
что x является постоянной.

Аналогично, частной производной от функции Z =
f(x,y) по переменной y, называется предел:

и обозначается одним из символов:

Частная производная от функции Z = f(x,y) по
переменной y — это производная от
функции Z = f(x,y) по переменной в предположении, что x = const..

Частные производные от функции нескольких
переменных находятся как производные от функции
одной переменной при условии, что все остальные
переменные считаются на момент
дифференцирования постоянными.

Частными производными второго порядка
от функции Z = f(x,y) называются частные
производные от частных производных первого
порядка: