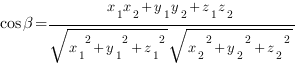Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
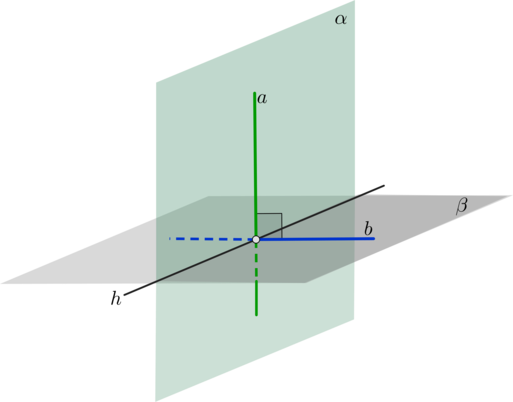
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
[{Large{text{Скрещивающиеся прямые}}}]
Заметим, что если две прямые лежат в одной плоскости, то, как и в планиметрии, они могут либо пересекаться, либо быть параллельны, либо совпадать. Значит, и угол между такими прямыми ищется так же, как и в планиметрии (напомним, что угол между параллельными прямыми считается равным (0^circ)). А если через две прямые нельзя провести одну плоскость?
Поэтому к трем видам взаимного расположения прямых в плоскости (пересекаются, параллелельны или совпадают) в пространстве добавляется еще один вид: скрещивающиеся прямые.
Определение
Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Угол (alpha) между прямыми — это угол (0^circleqslant
alphaleqslant
90^circ).
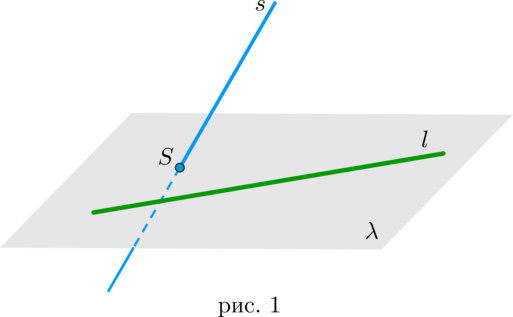
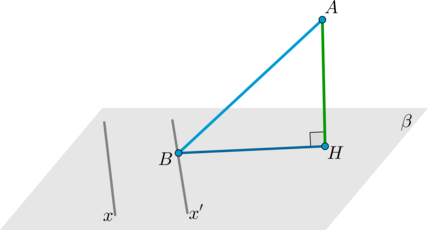
Теорема 1: признак скрещивающихся прямых
Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются (рис. 1).
Доказательство
Необходимо доказать, что через прямые (l) и (s) нельзя провести плоскость. Предположим, что это не так, то есть проведем через эти прямые плоскость (pi). Т.к. плоскость (pi) содержит прямую (l) и точку (S), то она совпадает с плоскостью (lambda) по следствию 1 из аксиом. Значит, т.к. прямая (s) лежит в плоскости (pi), то она лежит и в плоскости (lambda), что противоречит условию. Чтд.
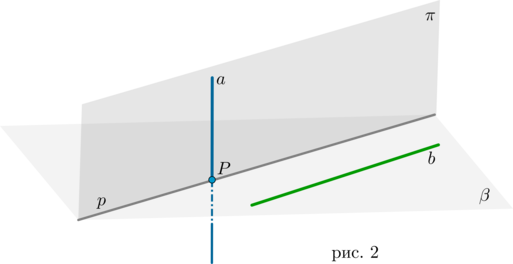
Теорема 2
Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой (рис. 2).
Доказательство
Пусть прямые (a) и (b) скрещиваются. Проведем плоскость (beta) через прямую (b) так, чтобы она пересекала прямую (a) в точке (P) (как в предыдущей теореме). Через точку (P) проведем прямую (pparallel b). Т.к. прямые (a) и (p) пересекаются (в точке (P)), то через них проходит единственная плоскость (назовем ее (pi)). Прямая (b) параллельна плоскости (pi) по признаку параллельности прямой и плоскости.
Построенная таким образом плоскость (pi) единственна. Любая другая плоскость, проходящая через прямую (a), будет уже пересекать прямую (p), а следовательно, будет пересекать прямую (b). Чтд.
[{Large{text{Угол между скрещивающимися прямыми}}}]
Определение
Угол между скрещивающимися прямыми – это угол между пересекающимися прямыми, соответственно параллельными двум скрещивающимся прямым.
Таким образом, можно определить следующий алгоритм нахождения угла между скрещивающимися прямыми (рис. 2):
Шаг 1. Через одну из двух скрещивающихся прямых (a) провести плоскость (pi) параллельно другой прямой (b) (по алгоритму, приведенному в теореме 2);
Шаг 2. В этой плоскости найти угол между прямыми (a) и (p) ((pparallel b)). Угол между ними будет равен углу между скрещивающимися прямыми (a) и (b).
[{Large{text{Перпендикулярность прямой и плоскости в пространстве}}}]
Определение
Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
Таким образом, перпендикулярными могут быть как и пересекающиеся прямые (лежащие в одной плоскости), так и скрещивающиеся прямые (не лежащие в одной плоскости).
Утверждение 1
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая перпендикулярна этой прямой:
[aparallel b, aperp c Longrightarrow bperp c]
Утверждение 2
Две прямые, перпендикулярные третьей прямой, не пересекаются (то есть либо параллельны, либо скрещиваются):
[aperp c, bperp c Longrightarrow acap b=varnothing]
Определение
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
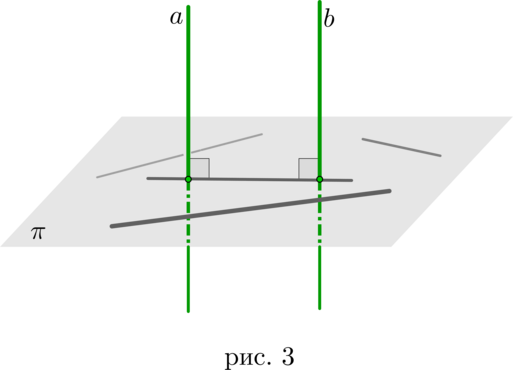
Следствие 1
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 3).
(Данное утверждение напрямую следует из утверждения 1.)
Верно и обратное утверждение:
Следствие 2
Если две прямые перпендикулярны плоскости, то они параллельны (рис. 3).
Теорема 3: признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
Доказательство
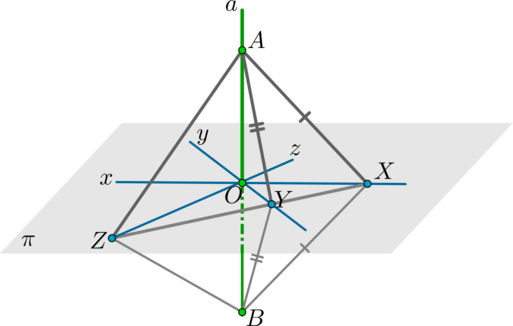
Пусть прямая (aperp x,aperp y), причем прямые (x, yin pi).
Предположим, что прямая (a) уже проходит через точку (O) пересечения прямых (x) и (y) (если это не так, то проведем через точку (A) прямую (a’), параллельную (a); если (a’) будет перпендикулярна плоскости, то и (a) будет ей перпендикулярна по следствию 1).
Проведем через точку (O) в плоскости (pi) некоторую прямую (z). Проведем также прямую, пересекающую прямые (x, y, z) в точках (X, Y,
Z) соответственно. На прямой (a) по разные стороны от плоскости (pi) отметим точки (A, B) так, чтобы (AO=OB).
Рассмотрим (triangle AXB). Т.к. (XO) – высота (по условию) и медиана (по построению), то (AX=XB). Аналогично для (triangle AYB): (AY=YB). Таким образом, (triangle AXY=triangle BXY) по трем сторонам. Отсюда (angle AXY=angle BXY).
Значит, по двум сторонам и углу между ними (triangle AXZ=triangle
BXZ). Значит, (AZ=BZ). Теперь (triangle AZB) – равнобедренный, причем (ZO) – медиана (по построению). Значит, (ZO) – высота, то есть прямая (a) перпендикулярна прямой (z).
Т.к. прямую (z) мы выбрали произвольно, то это значит, что прямая (a) перпендикулярна любой прямой из плоскости (pi), проходящей через точку (O). Но это значит, что прямая (a) перпендикулярна вообще любой прямой из плоскости, т.к. для любой прямой (z’), не проходящей через точку (O), существует параллельная ей прямая (z), проходящая через точку (O). А раз (aperp z, zparallel z’
Rightarrow aperp z’) (по утверждению 1).
Следствие 3
Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой, и притом только одну.
Следствие 4
Через любую точку пространства проходит прямая, перпендикулярная данной плоскости, и притом только одна.
[{Large{text{Расстояния}}}]
Определение
Пусть (aperp beta), причем (acap beta=H). Пусть (Ain a, Bin
beta):
Отрезок (AH) называется перпендикуляром к плоскости (beta).
Отрезок (AB) называется наклонной к плоскости (beta).
Отрезок (BH) называется проекцией наклонной (AB) на плоскость (beta).
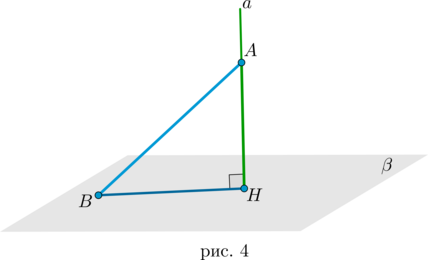
Расстояние от точки до плоскости
Длина перпендикуляра (AH) к плоскости (beta) равна расстоянию от точки (A) до плоскости (beta) (рис. 4).
Расстояние между параллельными плоскостями
Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
Заметим, что расстояние между пересекающимися плоскостями равно нулю.
Расстояние между скрещивающимися прямыми
Длина общего перпендикуляра (h) к обеим скрещивающимся прямым (a) и (b) и есть расстояние между этими скрещивающимися прямыми.
То есть (hperp a, hperp b).
Для того, чтобы найти расстояние между скрещивающимися прямыми, удобно найти расстояние между одной из них и плоскостью, проходящей через вторую прямую параллельно первой.
[{Large{text{Теорема о трех перпендикулярах (ТТП)}}}]
ТТП
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
Доказательство
1. Докажем, что из (xperp AB) следует, что (xperp BH).
Заметим, что т.к. (AHperp beta), то (AH) перпендикулярна любой прямой из плоскости (beta).
Проведем прямую (x’parallel x) через точку (B). Рассмотрим плоскость ((AHB)). Прямая (x’) перпендикулярна этой плоскости, т.к. перпендикулярна двум пересекающимся прямым (AB) и (AH) из этой плоскости. Но т.к. (xparallel x’), то и (xperp(AHB) Rightarrow
xperp BH).
2. Случай, когда из перпендикулярности проекции следует перпендикулярность наклонной, доказывается аналогично.
Замечание
Данная теорема является очень важным и незаменимым инструментов во многих задачах стереометрии.
[{Large{text{Угол между прямой и плоскостью. Угол между плоскостями}}}]
Определение
Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка ((0^circ;90^circ)).
Если прямая лежит в плоскости, то угол между ними считается равным (0^circ). Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен (90^circ).
Замечание
Таким образом, чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку (A) на этой прямой и провести перпендикуляр (AH) к плоскости. Если (B) – точка пересечения прямой с плоскостью, то (angle ABH) и есть искомый угол (рис. 4).
Определение
Двугранный угол – это геометрическая фигура, образованная прямой (a) (называемой ребром) и двумя полуплоскостями (называемыми гранями), общей границей которых является прямая (a).
Будем считать, что данные полуплоскости не принадлежат одной плоскости (т.к. в этом случае двугранный угол представляет собой просто плоскость с прямой из этой плоскости).
Если отметить по одной точке на каждой полуплоскости, а также две точки на прямой (a) (как показано на рисунке), то двугранный угол можно обозначить как (ABCD).
Замечание
Прямая (a) в данном случае является аналогом вершины плоского угла, а полуплоскости – аналогом сторон плоского угла.
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла.
Определение
Если к ребру (a) двугранного угла провести перпендикулярную плоскость (через любую точку), то она пересечет грани двугранного угла по лучам. Угол, образованный данными лучами, называется линейным углом данного двугранного угла.
Замечание
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла, которым соответствуют четыре линейных угла.
Градусная мера угла между данными плоскостями — это градусная мера меньшего из четырех линейных углов. Таким образом, данный угол принимает значения из промежутка ([0^circ;90^circ]).
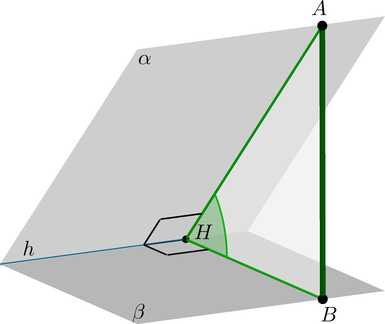
Для того, чтобы найти угол между плоскостями (alpha) и (beta), можно действовать по следующему алгоритму:
Отметить произвольную точку (A) в плоскости (alpha).
Провести (AHperp h), где (h) — линия пересечения плоскостей.
Провести (AB) перпендикулярно плоскости (beta).
Тогда (AB) – перпендикуляр к плоскости (beta), (AH) – наклонная, следовательно, (HB) – проекция. Тогда по ТТП (HBperp h).
Следовательно, плоскость, проходящая через прямые (AH) и (BH), и есть плоскость, перпендикулярная ребру (h) двугранного угла. Значит, (angle AHB) — линейный угол двугранного угла между плоскостями. Градусная мера этого угла равна градусной мере угла между плоскостями.
Заметим, что мы получили прямоугольный треугольник (triangle AHB). Как правило, находить (angle AHB) удобно из него.
[{Large{text{Перпендикулярность плоскостей}}}]
Определение
Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Теорема 4: признак перпендикулярности плоскостей
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Доказательство
Пусть прямая (a) лежит в плоскости (alpha) и перпендикулярна плоскости (beta). Докажем, что тогда плоскости (alphaperp beta).
Пусть плоскости пересекаются по прямой (h). Тогда (aperp h) (т.к. (a) перпендикулярна любой прямой из плоскости (beta), а (h), очевидно, лежит в (beta)). Проведем через точку пересечения прямых (a) и (h) прямую (b) в плоскости (beta). Углы, образованные при пересечении прямых (a) и (b) – линейные углы двугранных углов, образованных плоскостями (alpha) и (beta). Но (aperp b), значит, углы, образованные ими, равны (90^circ). Чтд.
25
Апр 2012
13 Задание (2022) (C2)

Если мы решили использовать этот метод, то будем придерживаться такого алгоритма:
1. Вводим систему координат.
2. Находим координаты направляющих векторов данных прямых.
3. По формуле косинуса угла между векторами находим косинус угла между направляющими векторами.
Косинус угла между векторами 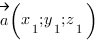
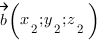
Вот, собствено, и все.
Важное уточнение: за угол между прямыми принимают меньший из двух углов, образованный этими прямыми, поэтому косинус угла между прямыми должен быть больше нуля, и он равен модулю косинуса угла между направляющими векторами.
Решим задачу.
В правильной шестиугольной призме 



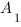
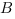
Длину отрезка 


Чтобы найти координаты вектора 
б) Найдем координаты направляющего вектора прямой 
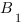
3. Найдем косинус угла 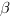


Ответ:
И.В. Фельдман, репетитор по математике.

|
Отзывов (9)
| Метки: решение задания С2