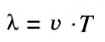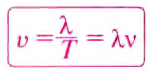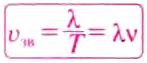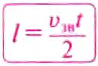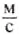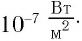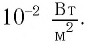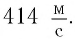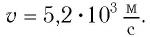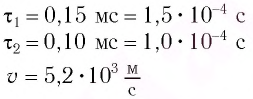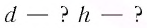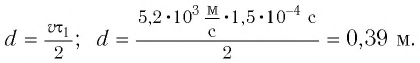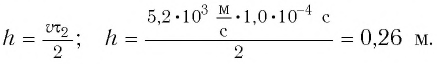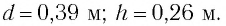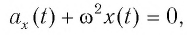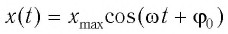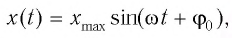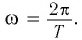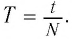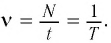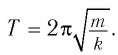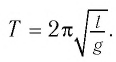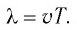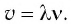Содержание
- Вычисление скорости звука в морской воде
- Основы лучевой теории распространения звука в океане
- Ослабление звука при распространении
- Шумы океана
Вычисление скорости звука в морской воде
Если в морской воде создать механические колебание её частиц, например, путём сжатия, то вследствие взаимодействия между ними эти колебания будут распространяться от частицы к частице с некоторой скоростью С. При этих условиях колебания распространяются в жидкости продольными волнами, т. е. каждая частица воды перемещается параллельно направлению распространения волны. Частицы жидкости, в которой распространяется волна, не будут ею переноситься, они будут лишь совершать колебания около своих положений равновесия. Распространяющиеся в воде слабые возмущения, т. е. колебания с малыми амплитудами, и называются звуковыми волнами.
Скорость распространения звуковых волн в жидкостях и газах равна:

где К — модуль объёмной упругости; ρ — плотность невозмущённой среды. Процесс деформации жидкости при распространении в ней звуковых волн может считаться адиабатным благодаря большой частоте колебаний. Модуль объёмной упругости в гидроакустике обычно заменяют коэффициентом сжимаемости Kaд:

где Kaд — коэффициент адиабатической сжимаемости.
Затем формулу (3.1) преобразуют, вводя в неё величины, удобные для расчётов:

где Kиз — изотермический коэффициент сжимаемости; Ср — теплоёмкость жидкости при постоянном давлении; Сv — то же при постоянном объёме.
Используя Kиз вместо Kaд и заменяя 1/ρ = α, где α — удельный объём, формула принимает вид:

Формула (3.4) называется теоретической. Для расчёта скорости звука по ней можно использовать уравнение состояния морской воды УС–80 для определения Kиз. Входящие в формулу (3.4) величины являются функциями температуры, солёности и гидростатического давления. Исследования формулы (3.4) показывают, что при увеличении температуры на 1 °С скорость звука в воде возрастает на 2,2 ÷ 4,7 м/с за счёт увеличения удельного объёма и уменьшения коэффициента сжимаемости.
При увеличении солёности на 1 епс скорость звука возрастает на 1,2 м/с, а при увеличении давления на 100 дбар (100 м) — на 1,8 м.
Формула (3.4) может обеспечить высокую точность определения скорости звука при условии достаточно точного определения Киз. Однако этот коэффициент, в свою очередь, является сложной функцией температуры, солёности и давления и не вычисляется теоретически. Это привело к необходимости найти эмпирические зависимости между скоростью звука, температурой, солёностью и давлением.
В общем случае эмпирические формулы имеют вид:

где Соп — скорость звука при атмосферном давлении и некоторых «опорных» значениях температуры и солёности, а ΔС — поправки к Соп за отклонение фактических значений температуры, солёности и давления от принятых при вычислении Соп.
Входящие в уравнение величины неоднократно определялись российскими и зарубежными исследователями. Наиболее точные и близкие к фактическим скоростям звука в морской воде дают вычисления по формулам В. Д. Вильсона с уточнениями А. С. Полосина, Х. Ф. Фрая и Дж. Д. Пага, Дель Гроссо и Чена и Миллеро. Краткое описание этих формул дано в работе. Из нее следует, что формула Дель Гроссо является наиболее точной и может быть использована для расчётов с погрешностью 0,05 м/с, а с поправочными коэффициентами, выведенными В. Н. Матвиенко и Ю. Ф. Тарасюком, точность расчётов может быть повышена до 0,01 м/с:

где CS,t,p — скорость звука, м/с; t — температура, °С; S — солёность, епс; р — гидростатическое давление, МПа.
При использовании эхолотов необходимо знать среднюю скорость звука в вертикальном направлении. Она рассчитывается как средняя взвешенная с учётом веса — толщины слоёв hi между горизонтами:

где hi — толщина слоёв, Сi — скорость звука в i-ом слое.
Найденное значение скорости используется для вычисления поправки, которую нужно ввести в измеренную эхолотом величину, так как эхолот рассчитан на С = 1500 м/с:

Основы лучевой теории распространения звука в океане
Лучевая теория является эффективным методом для изучения распространения звука в неоднородных средах, таких как океан, для случая достаточно высоких частот. Предполагается, что океан является горизонтально стратифицированным, в котором скорость звука зависит только от глубины, т. е. С = f (z). Поверхность и дно плоские и горизонтальные. Основой лучевой теории является предположение, что звуковая энергия в среде распространяется вдоль некоторых линий — лучей. Это можно представить себе как совокупность лучей, выходящих из излучателя звука (для простоты он предполагается точечным), и проходящих через малый замкнутый контур, лежащий в плоскости, перпендикулярной направлению распространения лучей.
Такая совокупность лучей будет образовывать лучевую трубку, в которой «течёт», не пересекая её стенок, звуковая энергия. Реальную физическую основу имеет световой луч, так как можно получить световой пучок диаметром в несколько десятых мм (т. е. в виде прямой линии). Звуковой луч имеет смысл лишь как нормаль к поверхности волны.
Для распространения звука в океане очень важное значение имеет даже не сама величина скорости звука, а профиль (форма) кривой С = f(z). В зависимости от типа профиля С = f(z) звук одной и той же частоты может распространяться на сотни и даже тысячи километров или на расстояние лишь нескольких километров. В однородной среде звуковые лучи будут представляться прямыми линиями. В слоистой среде, каковой и являются океаны, скорость звука при переходе из слоя в слой будет изменяться, так как будут меняться температура, солёность и давление. В этом случае, вводя понятие звуковых лучей для характеристики распространения звука, можно использовать известные законы геометрической оптики:

где i, β — углы падения и преломление звуковой волны; θ1, θ2 — углы скольжения.
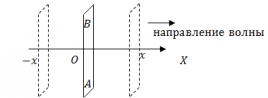
На рис. 3.1 показано изменение направления распространения звукового луча при переходе из слоя воды, где скорость звука равна С1 в слой воды со скоростью звука С2. Это явление, т. е. искривление звукового луча в неоднородной среде, получило название рефракции звуковых лучей.
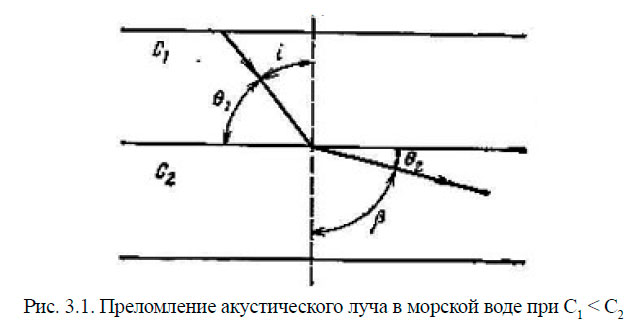
При распространении звука в воде со всё возрастающей скоростью углы скольжения будут непрерывно уменьшаться и при достижении слоя с некоторой критической скоростью Со станут равными нулю, т. е. преломлённая звуковая волна в этом слое отсутствует, другими словами, звук в этот слой не проникает. Это явление называется полным внутренним отражением. Величину критического угла скольжения можно найти из уравнения (3.9).
В океане скорость звука меняется в довольно широких пределах от ~ 1400 м/с до ~ 1600 м/с. При этом даже незначительные изменения скорости оказывают большое влияние на распространение звуковой волны в океане. Подчиняясь законам геометрической оптики, звуковые лучи в океане искривляются, принимая форму довольно сложных кривых.
Тип рефракции звука определяется характером вертикального распределения скорости звука (ВРСЗ). В методическом отношении сложную рефракционную картину удобно аппроксимировать сочетаниями двух основных типов рефракции звука в океане — положительной и отрицательной. Положительная рефракция наблюдается при увеличении скорости звука с глубиной, отрицательная — при убывании. Поскольку скорость звука зависит от температуры, солёности и давления (меньше всего на скорость влияет солёность, и пределы её изменения несравнимы с изменением температуры в верхних слоях и давления в нижних слоях океана), то тип рефракции будет определяться вертикальным распределением температуры. В глубинной зоне вертикальные градиенты и температуры, и солёности ничтожно малы, и там наблюдается монотонное увеличение скорости звука, обусловленное постоянным увеличением с глубиной гидростатического давления. На рис. 3.2, заимствованном из работы, показаны типы рефракции в зависимости от вертикального распределения температуры.
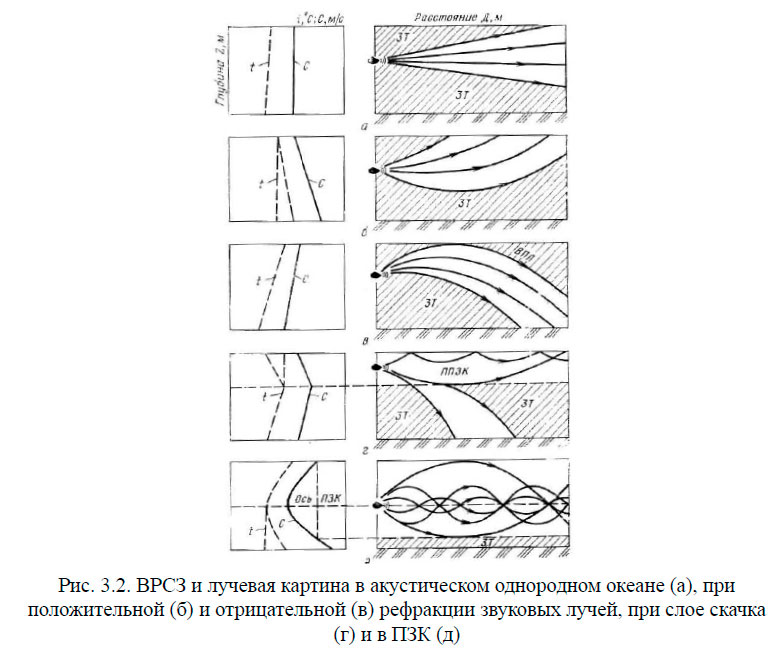
Положительная рефракция. Наблюдается обычно в холодное время года, когда температура воды в результате конвективного перемешивания становится одинаковой (изотермия) или повышается с глубиной (начало холодного периода года). Лучи, посланные в направлении дна, будут встречать слои воды с возрастающей скоростью звука. Это приводит к уменьшению углов скольжения, и при достижении критических углов будет наблюдаться полное внутреннее отражение лучей в толще воды и искривление их к поверхности (рис. 3.2, б).
Отрицательная рефракция. Наблюдается в тёплое время года при естественном для этого времени убывании температуры с глубиной. Лучи, направленные к поверхности, будут искривляться в сторону дна (рис. 3.2, в) В глубоководных районах и в мелководных с илистым дном дальность действия гидроакустических средств оказывается минимальной, ограниченной траекторией верхнего предельного луча. В мелком море при плотных грунтах звук может распространяться за счёт отражения от дна с колебанием уровня сигнала (донная подсветка), а иногда в тонком слое воды у дна происходит многократное отражение звука и образуется донный звуковой канал.
При наличии слоя скачка, образующегося в результате изотермии или инверсии температуры над ним и убывании температуры под ним в приповерхностном слое, рефракция будет положительной, а в нижележащем слое — отрицательной. На границе этих слоёв звуковой луч «расщепляется» и между его ветвями возникает зона акустической тени (3Т) (рис. 3.2, г). Если источник звука будет находиться над слоем скачка, то образуется приповерхностный звуковой канал с благоприятными условиями звукоподводной связи.
Для глубоководных районов Мирового океана типичным является профиль С(z), при котором на некоторой глубине располагается слой с минимальной скоростью звука. Вверх от этого слоя скорость растёт за счёт увеличения температуры, а вниз — за счёт роста гидростатического давления (рис. 3.2, д). Если поместить источник звука на горизонте с минимальной скоростью звука или вблизи него, то лучи, вышедшие из источника как в сторону поверхности, так и в сторону дна, будут встречать слои воды со всё возрастающей скоростью звука.
Достигнув критической скорости, лучи будут испытывать полное внутреннее отражение от выше- и нижележащих слоёв, многократно пересекая слой, в котором находится источник звука. Эта область в толще воды получила название подводный звуковой канал (ПЗК). Глубина, на которой скорость звука минимальная, называется осью ПЗК. Зона ПЗК ограничена лучами, выходящими из источника звука под углами скольжения ± θгр, которые определяются по формуле cos θгр ≈ Cк/Сгр, где Cк — скорость звука на оси ПЗК, Сгр — критическая скорость звука граничного луча (скорость звука на границах ПЗК). Лучи, выходящие из источника под меньшими углами скольжения, называются канальными.
ПЗК — это природный волновод, в котором существуют наиболее благоприятные условия для распространения звука, т. к. звуковая энергия распространяется концентрированно, не рассеиваясь на поверхности океана и не поглощаясь в донных грунтах. Максимальная дальность распространения звука зависит только от поглощения звука водой. Звук низких частот, для которых поглощение мало, может распространяться на тысячи километров.
Ось ПЗК обычно находится на глубинах 1000–1200 м; в тропической зоне ниже — до 2000 м; в умеренной зоне — 200–500 м; в полярных широтах — 100 м и выше. Скорость звука на оси ПЗК меняется от 1480–1490 м/с в низких широтах и до 1450–1460 м/с в высоких.
Ослабление звука при распространении
Распространение звуковых волн в воде сопровождается потерей части излученной звуковой энергии. Это обусловлено следующими факторами:
- потери на расширение фронта волны по мере удаления от источника звука;
- поглощение энергии водой в результате внутреннего трения и теплопроводности (переход в тепло);
- рассеивание по всевозможным направлениям случайными объёмными неоднородностями, присутствующими в воде.
Если область распространения звука кроме морской воды включает дно, взволнованную поверхность океана и морские льды, то ослабление звука ещё больше усложняется.
Таким образом, различные по своей природе явления приводят к одному и тому же эффекту — убыванию интенсивности звука по мере удаления от излучателя. Поэтому при изучении процесса ослабления звука при распространении можно измерить только суммарный эффект, обусловленный всеми факторами, который обычно называют затуханием звука.
Поскольку влияние разнообразных факторов на затухание звука пока не поддаётся теоретическим расчётам, то в результате многочисленных натурных измерений получены эмпирические формулы для расчёта коэффициента затухания звука в зависимости от частоты излучения, скорости звука и физических свойств воды: температуры, солёности, гидростатического давления (глубины) и водородного показателя pH (изменяется в пределах 7,6 ÷ 8,2).
В качестве примера приведём формулу для расчёта коэффициента затухания звука в ПЗК на частотах до 1 кГц:

где β — коэффициент затухания в дБ/км; βρ — не зависящий от частоты коэффициент затухания звука на низких частотах в дБ/км (зависит от типа водной массы и может меняться в пределах (0,2 ÷ 4,2) × 10-3); k — коэффициент, зависящий от pH (может меняться в пределах 0,5 ÷ 1,1); f — частота излучения.
Для диапазона частот от 20 Гц до 60 кГц коэффициент затухания можно определить по формуле:

Эмпирические формулы для расчёта коэффициента затухания для более высоких частот можно найти в работе.
Шумы океана
Важным акустическим параметром морской среды являются шумы океана. Они создают помехи нормальной работе гидроакустических средств, различаются по уровню, частотному составу, временным и другим характеристикам.
По источникам, вызвавшим шум, выделяют искусственные (преднамеренные) и естественные (собственные) шумы океана. Рассмотрим кратко собственные шумы.
Существуют следующие основные источники шумов:
1. Тепловые шумы, обусловленные движением молекул воды. Это постоянный источник шумов на частотах 50–200 кГц.
2. Динамические шумы. Производятся волнением, прибоем на берегу или рифах, течениями, дождём. Главным источником шума в глубоком океане на частотах 100 Гц – 50 кГц является ветровое волнение.
3. Подлёдные шумы связаны с динамикой ледяного покрова: движение льдин и ледяных полей, термическое растрескивание, торошение льда, обтекание ветром и течениями неровностей на его поверхности. «Шумят» айсберги при движении их из полярных районов в более тёплые.
4. Биологические шумы производятся представителями морской фауны: китовые, рыбы, ракообразные и беспозвоночные.
5. Сейсмические шумы вызываются землетрясениями, извержениями вулканов и отдалёнными штормами. Эти источники создают шумы на очень низких частотах (1–100 Гц).
Литература
Гидрометеорологическое Обеспечение Мореплавания — Глухов В.Г., Гордиенко А.И., Шаронов А.Ю., Шматков В.А. [2014]
Расстояние, пройденное за единицу времени звуковой волковой, распространяющейся через упругую среду
| Измерения звука | |
|---|---|
| Характеристика | Символы |
| Звуковое давление | p, SPL, L PA |
| Скорость частиц | v, SVL |
| Смещение частиц | δ |
| Интенсивность звука | I, SIL |
| Звуковая мощность | P, SWL, L WA |
| Звуковая энергия | W |
| Плотность звуковой энергии | w |
| Звуковое воздействие | E, SEL |
| Акустическое сопротивление | Z |
| Звуковая частота | AF |
| Потери при передаче | TL |
|
|
|
|
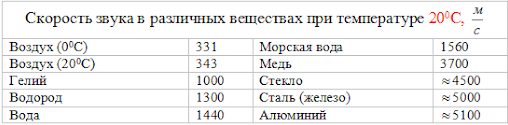
скорость звука — это расстояние, которое проходит через единицу времени ковая волна, когда она распространяется через упругую среду. При 20 ° C (68 ° F) скорость звука в воздухе составляет около 343 метров в секунду (1235 км / ч; 1125 футов / с; 767 миль / ч; 667 узлов), или километр за 2,9 с или милю в 4.7 с. Это сильно зависит от температуры, а также от среды, которая распространяется звуковая волна.
Скорость звука в идеальном газе зависит только от его температуры и состава. Скорость имеет слабую зависимость от частоты и давления в обычном воздухе, немного отклоня от идеального поведения.
В разговорной речи скорость звука относится к скорости звуковых волн в воздухе. Однако скорость звука рассматривается от вещества к веществу: обычно звук распространяется медленнее всего в газах, быстрее в жидкостях и еще быстрее в твердых телах. Например, как указано выше, он распространяется по воздуху со скоростью 343 м / с, он распространяется со скоростью 1481 м / с в воде (почти в 4,3 раза быстрее) и со скоростью 5120 м / с в железе (почти в 15 раз быстрее). Быстрее). В исключительно жестком материале, таком как алмаз, звук распространяется со скоростью 12 000 метров в секунду (39 000 футов / с), что примерно в 35 превышает скорость в воздухе и является максимальной скоростью, которую он может распространять в нормальных условиях.
Звуковые волны в твердых телах состоят из волн (как в газах и жидкостях) и звуковой волны другого типа, называемой поперечной волной, которая возникает только в твердых телах. Как показано в сейсмологии, поперечные волны в твердых телах обычно происходят с разными скоростями. Скорость сжатия волн в твердых телах определяет сжимаемостью среды, модулем сдвига и плотностью. Скорость поперечного волн определяется только модулем сдвига и плотностью твердого материала.
В гидродинамике скорость звука в текучей среде (газе или жидкости) используется в качестве относительной меры для скорости объекта, движущегося через среду. Отношение скорости объекта к скорости звука в жидкости называется число Маха объекта. Объекты, движущиеся со скоростью, превышающая число Маха1, считаются движущимися со скоростью сверхзвуковой.
Содержание
- 1 История
- 2 Основные концепции
- 2.1 Сжатие и поперечные волны
- 3 Изменение
- 4 Зависимость от среды
- 5 Зависимость высоты и последствия для атмосферной акустики
- 6 Практическая формула для сухого воздуха
- 7 Подробная информация
- 7.1 Скорость звука в идеальных газах и воздухе
- 7.2 Воздействие сдвига ветра
- 7.3 Таблицы
- 8 Влияние частоты и состава газа
- 8.1 Общие физические соображения
- 8.2 Практическое применение в воздухе
- 9 Число Маха
- 10 Экспериментальные методы
- 10.1 Методы однократной синхронизации
- 10.2 Другие методы
- 10.3 Высокоточные измерения в воздухе
- 11 Негазообразные среды
- 11.1 Скорость звука в твердых телах
- 11.1.1 Трехмерные твердые тела
- 11.1.2 Одномерные твердые тела
- 11.2 Скорость звука в жидкостях
- 11.2.1 Вода
- 11.2.2 Морская вода
- 11.3 Скорость звука в плазме
- 11.1 Скорость звука в твердых телах
- 12 Градиенты
- 13 См. Также
- 14 Ссылки
- 15 Внешние ссылки
История
Сэр Исаак Ньютон 1687 Princi pia включает вычисление скорости звука в воздухе как 979 футов в секунду (298 м / с). Это слишком мало примерно на 15%. Несоответствие вызвано, прежде всего, пренебрежением (тогда неизвестным) эффектом быстро меняющейся температуры в звуковой волне (в современной терминах стрессе и расширении воздуха звуковой волной — это адиабатический процесс, а не изотермический процесс ). Эта ошибка была позже исправлена Лапласом.
В течение 17 века было несколько попыток точно измерить скорость звука, включая технологию Марина Мерсенна в 1630 году (1380 парижских футов в секунду), Пьер Гассенди в 1635 году (1473 парижских фута в секунду) и Роберт Бойль (1125 парижских футов в секунду). В 1709 году преподобный Уильям Дерхам, ректор Апминстера, опубликовал более точные данные о скорости звука: 1072 парижских футов в секунду. (Парижская стопа составляющая 325 мм. Этонее, чем стандартная «международная стопа», широко используемая сегодня, официально определена в 1959 году как 304,8 мм, что означает скорость звука при 20 ° C (68 ° F) 1055 парижских футов в секунду).
Дерхэм использовал телескоп с башни церкви Святого Лаврентия, Апминстер, чтобы наблюдать вспышку выстрела из дробовика, а измерил время, пока он не услышал выстрел из пистолета. полсекундный маятник. Были произведены замеры выстрелов из других источников, включая церковь Северный Окендон. Расстояние было с помощью триангуляции, и, таким образом, было рассчитано распространение звука.
Основные понятия
Передача звука может быть проиллюстрирована с помощью моделей состоящий из сферических объектов, связанных между собой пружинами.
В реальном материальном плане частицы молекулы материала, а пружины представляют собой связи между ними. Звук проходит через систему, сжимая и расширяя пружины, передавая акустическую соседним сферам. Это помогает энергоснабжению, в свою очередь, пружинам (связям) соседней сферы и так далее.
Скорость звука через модель зависит от жесткости / жесткости пружин и массы сфер. Пока расстояние между сферами остается постоянным, жесткие пружины / связи передают энергию быстрее, в то время как более крупные сферы передают медленнее.
В реальном материале жесткость пружин известна как «модуль упругости », а масса плотности материала. При прочих равных условиях (при прочих равных условиях ) звук будет распространяться медленнее в пористых материалах и быстрее в более жестких. Такие эффекты, как дисперсия и отражение, также можно понять с помощью этой модели.
. Например, звук в никеле распространяется в 1,59 раза быстрее, чем в бронзе, из-за большей жесткости никеля примерно при такой же плотности. Точно так же звук распространяется примерно в 1,41 раза быстрее в газе легкого водорода (протий ), чем в газе тяжелого водорода (дейтерий ), поскольку дейтерий имеет аналогичные свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых жидкостях, чем в газах, что твердые тела сложнее сжимать, чем жидкость, а жидкость, в свою очередь, труднее сжимать. чем газы.
В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это понятие проиллюстрировано представлением данных для трех материалов, таких как воздух, вода и сталь, каждый из которых имеет разную сжимаемость, что более чем компенсирует разницу в плотности. Наглядным примером этих двух эффектов является всего в 4,3 раза больше, чем в воздухе, несмотря на огромные различия в сжимаемости двух сред. Причина в том, что большая плотность воды, сокращает объем воды в воде по сравнению с воздухом, почти компенсирует разницу в сжимаемости двух сред.
Практический пример можно наблюдать в Эдинбурге, когда в восточной части Эдинбургского замка стреляют из «Пистолета на час». Стоя у подножия западной оконечности Касл-Рока, звук ружья можно услышать сквозь скалу, незадолго до того, как он прибудет по воздуху, частично задержанный немного более длинным маршрутом. Это особенно эффективно, если производится салют из нескольких пистолетов, например, «День рождения королевы».
волны сжатия и поперечные волны


в газе или жидкости звук из волн сжатия. В твердых телах волны распространяются двух разных типов. Продольная волна использует со сжатием и декомпрессией в направлении движения и представляет собой тот же процесс в газах и жидкостях, с аналогичной волной типа сжатия в твердых телах. В газах и жидкостях поддерживаются только волны сжатия. Дополнительный тип волны, поперечная волна, также называемая поперечной волной, возникает только в твердых телах, потому что только твердые тела упругие деформации. Это связано с упругой деформацией среды перпендикулярно вокруг волны; направление деформации сдвига называется «поляризацией » этого типа волны. В общем, поперечные волны создают как пара ортогональных поляризаций.
Эти разные волны (волны сжатия и разные поля поперечных волн) могут иметь разные скорости на одной и той же частоте. Следовательно, они прибывают к наблюдателю в разное время, крайним примером является землетрясение , когда сначала приходят резкие волны сжатия, а секунды спустя — колебательные поперечные волны.
Скорость волны сжатия в жидкости определяется сжимаемостью и плотностью среды. В твердых телах волны сжатия аналогичны волнам в жидкостях, в зависимости от сжимаемыми факторами модуля сдвига, который влияет на эффективность сжатия из-за внеосевой упругой энергии. при сжатии. Скорость сдвиговых волн, которые могут возникнуть только в твердых телах, определяется просто модулем сдвига и плотностью твердого материала.
Уравнения
Скорость звука в математической системе обозначения условно обозначается буквой c, от латинского celeritas, означающего «скорость».
Для жидкостей в целом скорость звука c определяется уравнением Ньютона — Лапласа:
- c = K s ρ, { displaystyle c = { sqrt { frac {K_ {s})} { rho} }},}
где
- Ks- коэффициент жесткости, изэнтропический модуль объемной упругости (или модуль объемной упругости для газов);
- ρ { displaystyle rho}
— это плотность.
Таким образом, скорость звука увеличивает жесткость (сопротивление упругого тела деформации под действием приложенной силы) материала. Для идеальных газов объемный модуль K — это просто давление газа, умноженное на безразмерный показатель адиабаты, который составляет около 1,4 для воздуха при нормальных условиях давления и температуры.
Для <общих состояний, если используется классическая механика, скорость звука c получена следующим образом:
Рассмотрим звук волны, распространяющаяся по трубе с площадью поперечного сечения A { displaystyle A}




- dvdt = — 1 ρ dpdz → dp = (- ρ dv) dzdt = (vd ρ) v → v 2 ≡ с 2 знак равно dpd ρ { displaystyle { begin {align} { frac {dv} {dt}} = — { frac {1} { rho}} { frac {dp} {dz}} \ rightarrow dp = (- rho dv) { frac {dz} {dt}} = (vd rho) v \ rightarrow v ^ {2} Equiv c ^ {2} = { frac {dp} {d rho}} end {align}}}
И поэтому:
- c = (∂ p ∂ ρ) s, { displaystyle c = { sqrt { left ({ frac { partial p} { partial rho}} right) _ {s}}},}
где
- p — давление;
- ρ { displaystyle rho}
— плотность, а производная берется изоэнтропически, то есть есть при энтропии s. Это звуковая волна распространяется так быстро, что ее распространение можно представить как адиабатический процесс.
Если релятивистские эффекты важны, скорость звука рассчитывается по релятивистским уравнениям Эйлера.
В недисперсионной среде скорость звука не зависит от частоты звука, поэтому скорости передачи и распространения звука одинаковы для всех частот. Воздух, смесь кислорода и азота, представляет собой недиспергирующую среду. Однако воздух действительно содержит небольшое количество CO 2, который является диспергирующей средой и вызывает дисперсию в воздухе на ультразвуковых частотах (>28 кГц ).
в диспергирующая среда, скорость звука представляет собой функцию частоты звука через дисперсионное соотношение. Каждая частотная компонента распространяется со своей собственной скоростью, называемой фазовой скоростью, в то время как энергия возмущения распространяется с групповой скоростью . То же явление происходит и со световыми волнами; см. Описание в оптической дисперсии.
Зависимость от среды
Скорость звука переменная и зависит от свойств В твердом телах скорость поперечного (или поперечного) волн зависит от деформации сдвига под действием сдвига (называется модулем сдвига ) и плотностью среды. х зависит от тех же двух факторов, что и добавление зависимости от сжимаемости.
жидкостей только сжимаемость и плотность среды являются важными факторами, поскольку жидкость не передают напряжение сдвига. В гетерогенных жидкостях, таких как жидкость, наполненная пузырьками газа, плотность жидкости и сжимаемость газа аддитивно влияние на скорость звука, как показано в эффекте горячего шоколада.
В газах, адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (индекс адиабаты), в то время как давление и обратно пропорциональны температуре и молекулярной массе, поэтому важны только полностью независимые свойства температуры и молекулярной структуры. (Коэффициент теплоемкости может определяться температурой и молекулярной структурой, но простой молекулярной массы недостаточно для его определения).
Звук распространяется быстрее в газах с низкой молекулярной массой, таких как гелий, чем в более тяжелых газах, таких как ксенон. Для одноатомных газов скорость звука составляет около 75% от средней скорости движения элементов в этом газе.
Для данного идеального газа молекулярный состав фиксирован, и таким образом скорость звука зависит только от его температуры. При постоянной температуре газа давление не влияет на скорость звука, плотность больше, так как давление и плотность (также пропорциональная давлению) равны, но противоположны влияют на скорость звука, и эти два вклада полностью компенсируются. Аналогичным образом, волна сжатия в твердой телах зависит как от сжимаемости, так и от плотности — как и в жидкостях, — но в газах плотность сжимаемости таким образом, что некоторая часть каждого атрибута учитывается, изменяет зависимость от температуры, молекулярная масса и коэффициент теплоемкости, которые могут быть независимо получены из температуры и молекулярного состава (см. выводы ниже). Таким образом, для одного данного газа (при условии, что молекулярная масса не изменяется) и в небольшом диапазоне температур (для которого теплоемкость относительно постоянна) скорость звука становится зависимой только от температуры газа.
В режиме поведения неидеального газа, для которого будет использоваться буква газа Ван-дер-Ваальса, пропорциональность не точной, и существует небольшая зависимость скорости звука от давления газа.
Влажность оказывает небольшое, но измеримое влияние на скорость звука (вызывая ее увеличение примерно на 0,1–0,6%), потому что молекулы кислорода и азот воздух заменяется более легкими молекулами воды. Это простой эффект смешивания.
Изменение высоты и последствия для атмосферной акустики

В атмосфере Земли главным фактором, влияющим на скорость звука, является температура. Для данного идеального газа с постоянной теплоемкостью и составом скорость звука зависит исключительно от температуры; см. Подробности ниже. В таком идеальном случае эффекты пониженной плотности и пониженного давления на высоте компенсируют друг друга, за исключением остаточного эффекта температуры.
Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до 11 км, звук преломляется вверх, вдали от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника. Уменьшение скорости звука с высотой упоминается как отрицательный градиент скорости звука.
. Однако есть вариации в этой тенденции выше 11 км. В частности, в стратосфере выше примерно 20 км скорость звука увеличивается с высотой из-за увеличения температуры в результате нагрева внутри озонового слоя. Это дает положительный градиент скорости звука в этой области. Еще одна область положительного градиента наблюдается на очень больших высотах, в хорошо названной термосфере выше 90 км.
Практическая формула для сухого воздуха
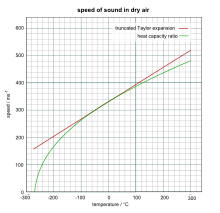
Приблизительную скорость звука в сухом (влажность 0%) воздухе в метрах в секунду при температуре около 0 ° C можно рассчитать по формуле
- cair = (331,3 + 0,606 ⋅ ϑ) м / с, { displaystyle c _ { mathrm {air}} = (331,3 + 0,606 cdot vartheta) ~~~ mathrm {m / s},}
где ϑ { displaystyle vartheta }
Это уравнение получено из первых двух членов разложения Тейлора следующее более точное уравнение:
- cair = 331,3 1 + ϑ 273,15 м / с. { displaystyle c _ { mathrm {air}} = 331.3 ~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~~ mathrm {m / s}.}
Деление первая часть и умножение второй части в правой части на √273,15дает точно эквивалентную форму
- cair = 20,05 ϑ + 273,15 м / с. { displaystyle c _ { mathrm {air}} = 20.05 ~ { sqrt { vartheta +273.15}} ~~~~ mathrm {m / s}.}
, который также можно записать как
- cair = 20,05 T м / с { displaystyle c _ { mathrm {air}} = 20,05 ~ { sqrt {T}} ~~~~ mathrm {m / s}}
где T обозначает термодинамический показатель.
Значение 331,3 м / с, которое представляет скорость при 0 ° C (или 273,15 K), основано на теоретических (и некоторых измеренных) значениях коэффициент теплоемкости, γ, а также тот факт, что при 1 атм реальный воздух очень хорошо описывается приближением идеального газа. Обычно найденные значения скорости звука при 0 ° C могут обсуждаться от 331,2 до 331,6 из-за допущений, сделанных при ее расчетах. Если принять γ идеального газа равным 7/5 = 1,4, то скорость при 0 ° C вычисляется (см. Раздел ниже) и составляет 331,3 м / с, коэффициент, использованный выше.
Это уравнение верно для более широкого диапазона температур, но все же зависит от приближения отношений теплоемкости, не зависящего от температуры, и по этой причине не будет работать особенно при более высоких температурах. Он дает хорошие прогнозы в относительно сухих, холодных условиях низкого давления, таких как стратосфера Земли. Уравнение не работает при низких давлениях и коротких длинах волн из-за предположения, что длина волны звука в газе намного больше, чем средняя длина свободного пробега между столкновениями молекул газа. Вывод этих условий будет дан в следующем разделе.
График, на котором сравниваются результаты двух соотношений справа, с немного другим размером 331,5 м / с для скорости звука при 0 ° C.
Подробности
Скорость звука в идеальных газах и воздухе
Для идеального газа K (модуль объемной упругости в уравнениях выше, эквивалентный C, коэффициент жесткости в твердых телах) определяется как
- K = γ ⋅ p, { displaystyle K = gamma cdot p,}
таким образом, из уравнения Ньютона — Лапласа, приведенного выше, скорость звука в идеальном газе определяется как
- c = γ ⋅ p ρ, { displaystyle c = { sqrt { gamma cdot {p over rho}}},}
, где
- γ — индекс адиабаты, также известный как коэффициент изоэнтропического расширения. Это отношение удельной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме (C p / C v { displaystyle C_ {p} / C_ {v}}
) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;
- p равно давление ;
- ρ — это плотность.
. Используя закон идеального газа для замены p на nRT / V, и заменяя ρ на nM / V, уравнение для идеального газа становится
- cideal = γ ⋅ p ρ = γ ⋅ R ⋅ TM = γ ⋅ K ⋅ T м, { displaystyle c _ { mathrm {ideal}} = { sqrt { gamma cdot {p over rho}}} = { sqrt { gamma cdot R cdot T over M }} = { sqrt { gamma cdot k cdot T over m}},}
где
- cидеально — скорость звука в идеальном газе ;
- R (приблизительно 8, 314463 Дж · К · моль) — молярная газовая постоянная (универсальная газовая постоянная);
- k — постоянная Больцмана ;
- γ (гамма) — индекс адиабаты. При комнатной температуре, когда тепловая энергия полностью распределяется на вращение (полностью возбуждаются), но квантовые эффекты предотвращают возбуждение колебательных мод, согласно кинетической теории составляет 7/5 = 1.400 для двухатомных молекул. Гамма фактически измеряется экспериментально в диапазоне от 1,3991 до 1,403 при 0 ° C для воздуха. Гамма составляет точно 5/3 = 1,6667 для одноатомных газов, таких как благородные газы, и приблизительно 1,3 для газов с трехатомными молекулами;
- T — абсолютная температура;
- M — молярная масса газа. Средняя молярная масса для сухого воздуха составляет около 0,028 964,5 кг / моль;
- n — число молей;
- m — масса отдельной молекулы.
Некоторые другие условия, отмеченные как указано ниже, представлены некоторые другие условия, определенные ниже. Было обнаружено, что расчетные значения для c воздуха незначительно отличаются от экспериментально значения.
Ньютон, как известно, считал скорость звука до большей части разработки термодинамики и т. Д. неправильно использовались изотермические вычисления вместо адиабатических. В его отсутствовал коэффициент γ, но в остальном он был правильным.
Численная замена приведенных выше значений дает идеальное газовое приближение скорости звука для газов, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне Земли на уровне моря). Кроме того, для двухатомных газов использование γ = 1,4000 требует, чтобы газ существовал в достаточно высоком температурном диапазоне, чтобы вращательная теплоемкость была полностью возбуждена (т.е. вращение молекул полностью использовалось в качестве «перегородки» или резервуара тепловой энергии); Но в то же время должна быть достаточно низкая, чтобы колебательные моды не вносили свой вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, так как все колебательные квантовые моды выше моды минимальной энергии имеют слишком высокую энергию, заселить значительное количество молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температуре значительно ниже комнатной (см. Таблицы ниже). См. Раздел о газах в удельной теплоемкости для более полного обсуждения этого явления.
Для воздуха вводим сокращение
- R ∗ = R / M a i r. { displaystyle R _ {*} = R / M _ { mathrm {air}}.}
Кроме того, мы переключаемся на температуру по Цельсию ϑ { displaystyle vartheta}
- cair = γ ⋅ R ∗ ⋅ T = γ ⋅ R ∗ ⋅ (ϑ + 273.15), { displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R_ { *} cdot T}} = { sqrt { gamma cdot R _ {*} cdot ( vartheta +273.15)}},}
- cair = γ ⋅ R ∗ ⋅ 273,15 ⋅ 1 + ϑ 273,15, { displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R _ {*} cdot 273.15}} cdot { sqrt {1 + { frac { vartheta} {273.15}}}},}
где ϑ { displaystyle vartheta}
Подстановка числовых значений
- R = 8,314 463 Дж / (моль ⋅ K) { displaystyle R = 8.314 , 463 ~ mathrm {J / (mol cdot K)}}
для молярная газовая постоянная в Дж / моль / Кельвин и
- M воздух = 0,028 964 5 кг / моль { displaystyle M _ { mathrm {air}} = 0,028 , 964 , 5 ~ mathrm {кг / моль}}
для средней молярной массы воздуха в кг; и используя идеальное значение двухатомного газа γ = 1,4000, мы имеем
- c a i r = 331,3 1 + 273,15 м / с. { displaystyle c _ { mathrm {air}} = 331.3 ~~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~ mathrm {m / s}.}
Наконец, Разложение Тейлора оставшегося квадратного корня в ϑ { displaystyle vartheta}
- cair = 331,3 (1 + ϑ 2 ⋅ 273,15) м / с, { displaystyle c _ { mathrm {air}} = 331,3 ~ (1 + { frac { vartheta} {2 cdot 273.15}}) ~~~ mathrm {m / s},}
- cair = ( 331,3 + 0,606 ⋅ ϑ) РС. { displaystyle c _ { mathrm {air}} = (331.3 + 0.606 cdot vartheta) ~~~ mathrm {m / s}.}
Приведенный выше вывод включает первые два уравнения, приведенные в «Практической формуле для сухого воздуха »выше.
Эффекты сдвига ветра
Скорость звука зависит от температуры. Временная температура и скорость звука обычно снижаются от высоты, звук преломляется вверх, вдали Сдвиг ветра 4 м / (с · км) может вызвать рефракцию, равную типичную температуру градиент 7,5 ° C / км, слушателей на земле, создаваемая акустическая тень. Более высокие значения градиента ветра преломлять звук вниз к поверхности в подветренном направлении, устраняя акустическую тень на подветренной стороне.>
Для распространения звука экспоненциальное изменение скор ости ветра с высотой можно определить следующим образом:
- U (h) = U (0) h ζ, { Displaystyle U (час) = U (0) час ^ { zeta},}
- d U d H (час) = ζ U (час) час, { displaystyle { frac { mathrm {d} U} { mathrm {d} H}} (h) = zeta { frac {U (h)} {h}},}
где
- U (h) — скорость ветра при высоте h;
- ζ — экспоненциальный коэффициент, основанный на шероховатости поверхности земли, обычно от 0,08 до 0,52;
- dU / dH (h) — ожидаемый градиент ветра на высоте h.
В 1862 г. Гражданской войны в США Битва при Юке акустическая тень, усиленная северо-восточным ветром, удерживала две дивизии солдат Союза вне боя, потому что они могли не слышно звуков боя только в 10 км по ветру.
Таблицы
В стандартной атмосфере :
- T0составляет 273,15 K (= 0 ° C = 32 ° F), что дает теоретическое значение 331,3 м / с (= 1086,9 фут / с = 1193 км / ч = 741,1 миль / ч = 644,0 узлов ). Однако значения в диапазоне от 331,3 до 331,6 м / с можно найти в справочной литературе;
- T20равно 293,15 K (= 20 ° C = 68 ° F), что дает значение 343,2 м / с (= 1126,0 фут / с = 1236 км / ч = 767,8 миль / ч = 667, 2 kn );
- T25равно 298,15 K (= 25 ° C = 77 ° F), что дает значение 346,1 м / с (= 1135,6 фут / с = 1246 км / ч = 774,3 миль / ч = 672,8 kn ).
Фактически, предполагаемая идеальный газ, скорость звука зависит только от температуры, не от давления или плотности (они изменяются в шаг Воздух — почти идеальный газ. Температура воздуха меняется с высотой, что дает следующие изменения скорости звука при стандартных стандартах — фактические условия могут отличаться.
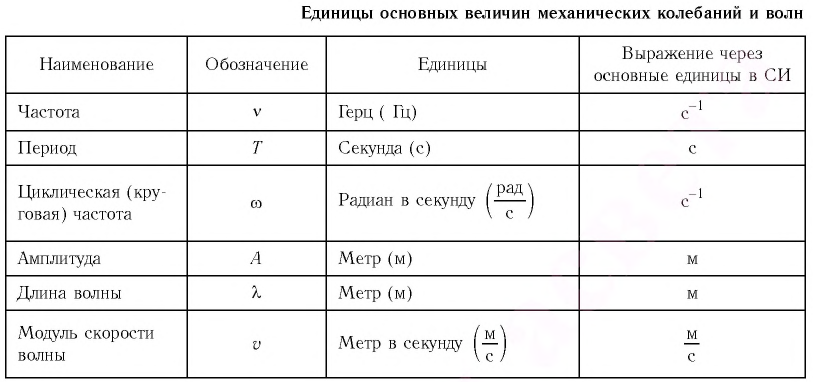
| Температура. T (°C ) | Скорость звука. c (m /s ) | Плотность воздуха. ρ (kg /m ) | Характеристическое удельное акустическое сопротивление. z0(Pa ·s /m ) |
|---|---|---|---|
| 35 | 351,88 | 1.1455 | ) 403,2 |
| 30 | 349.02 | 1.1644 | 406,5 |
| 25 | 346,13 | 1,1839 | 409,4 |
| 20 | 343,21 | 1,2041 | 413,3 |
| 15 | 340,27 | 1,2250 | 416,9 |
| 10 | 337,31 | 1,2466 | 420,5 |
| 5 | 334,32 | 1,2690 | 424,3 |
| 0 | 331,30 | 1,2922 | 428,0 |
| −5 | 328,25 | 1.3163 | 432,1 |
| −10 | 325.18 | 1.3413 | 436,1 |
| -15 | 322,07 | 1,3673 | 440,3 |
| −20 | 318.94 | 1,3943 | 444,6 |
| −25 | 315,77 | 1,4224 | 449,1 |
При нормальных атмосферных условиях, температуре и, следовательно, скорости звука, зависит от высоты:
| Высота | Температура | м / с | км / ч | миль / ч | kn |
| Уровень моря | 15 ° C (59 ° F) | 340 | 1,225 | 761 | 661 |
| 11000 м − 20 000 м. (крейсерская высота коммерческих самолетов,. и первый сверхзвуковой полет ) | -57 ° C (-70 ° F) | 295 | 1062 | 660 | 573 |
| 29000 м ( Полет X-43A ) | -48 ° C (-53 ° F) | 30 1 | 1,083 | 673 | 585 |
Влияние частоты и состава газа
Общие физические соображения
Среда, в которой звук распространяющаяся волна не всегда реагирует адиабатически, и в результате скорость звука может изменяться с частотой.
Ограничения концепции скорости звука из-за чрезмерного затухания также вызывают озабоченность. Затухание, которое существует на уровне моря для высоких частот, применяется к последовательно более низким частотам по мере уменьшения атмосферного давления или увеличения средней длины свободного пробега. По этой причине концепция скорости звука (за исключением частот, приближающихся к нулю) постепенно теряет свой диапазон применимости на больших высотах. Стандартные уравнения для скорости звука применимы с разумной точностью только к ситуациям, в которых длина звуковой волны значительно больше, чем длина свободного пробега молекул в газе.
Молекулярный состав газа влияет как на массу (M) молекул, так и на их теплоемкость, и поэтому оба фактора влияют на скорость звука. В общем, при той же молекулярной массе одноатомные газы имеют немного более высокую скорость звука (более чем на 9%), потому что у них более высокая γ (5/3 = 1,66…), чем у диатомовых (7/5 = 1,4). Таким образом, при той же молекулярной массе скорость звука одноатомного газа возрастает в
- раз, одноатомный газ, двухатомный = 5/3 7/5 = 25 21 = 1,091… { displaystyle {c _ { mathrm {газ, одноатомный}} over c _ { mathrm {газ, двухатомный}}} = { sqrt {{5/3} over {7/5}}} = { sqrt {25 over 21}} = 1.091 ldots}
Это дает разницу в 9% и будет типичным соотношением скоростей звука при комнатной температуре в гелии vs. дейтерий, каждый с молекулярной массой 4. Звук в гелии распространяется быстрее, чем в дейтерии, потому что адиабатическое сжатие нагревает гелий больше, поскольку молекулы гелия могут накапливать тепловую энергию от сжатия только при поступательном движении, но не при вращении. Таким образом, молекулы гелия (одноатомные молекулы) быстрее перемещаются в звуковой волне и быстрее передают звук. (Звук распространяется со скоростью примерно 70% от средней молекулярной скорости в газах; этот показатель составляет 75% в одноатомных газах и 68% в двухатомных газах).
Обратите внимание, что в этом примере мы предположили, что температура достаточно низкая, чтобы на теплоемкость не влияла молекулярная вибрация (см. теплоемкость ). Однако вибрационные режимы просто вызывают гаммы, которые уменьшаются до 1, поскольку колебания в многоатомном газе дают дополнительные возможности хранения тепла, которые не влияют на скорость молекулы и скорость звука. Таким образом, влияние более высоких температур и колебательной теплоемкости увеличивает разницу между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.
Практическое применение к воздуху
Безусловно, важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню из абсолютной температуры, что дает увеличение примерно на 0,6 м / с на градус Цельсия. По этой причине высота звука музыкального духового инструмента создается с помощью его температуры.
Скорость звука увеличивается из-за газа, но уменьшается из-за углекислого газа. Разница между влажностью 0% и 100% составляет около 1,5 м / с при стандартном давлении и температуре, но величина эффекта зависит от температуры. Содержание углекислого газа в воздухе не фиксировано как из-за загрязнения углерода, так и из-за человеческого дыхания (например, в воздухе, продуваемом духовыми инструментами).
В практических приложениях зависимости от частоты и давления обычно незначительна. В сухом воздухе скорость звука увеличивается примерно на 0,1 м / с при повышении частоты с 10 до 100 Гц. Для слышимых частот выше 100 Гц он относительно постоянен. Стандартные значения скорости звука указаны в пределе низких частот, где длина волны больше по сравнению со средней длиной свободного пробега.
Как показано выше, приблизительное значение 1000/3 = 333,33… м / с точно ниже 5 ° C и приблизительное для всех «обычных» наружных температур (по крайней мере, в умеренном климате)), отсюда обычное практическое правило для определения того, как далеко ударила молния: отсчитывайте секунды от начала вспышки молнии до начала применения раскатки грома и раздела на 3: результат — расстояние в километрах до ближайшей точки удара молнии.
Число Маха

Число Маха, полезная величина в аэродинамике, это отношение воздуха 342>скорость до качества Однако летательные аппараты летательных аппаратов перепад давления для вычислений числа Маха, а не Температура, следовательно, стандартная температура, благодаря чему давление за усилием, воспринимаемое трубкой Пито, также зависит от высоты как скорость.
Экспериментальные методы
Существуют
Самая ранняя достаточно точная оценка скорости звука в воздухе была сделана Уильямом Д ерхемом и подтвержден Исааком Ньютоном. У Дерхама был телескоп на вершине башни церкви Святого Лаврентия в Апминстере, Англия. анные карманные часы по помощнику, который стрелял из дробовика заранее определенное время с заметной точки за несколько миль от дома, через сельскую местность. Это может быть подтверждено телескопом. Затем он измерил интервал между появлением дыма и появлением звука с помощью полусекундного маятника. Расстояние от места выстрела определялось путем триангуляции, а простое деление (расстояние / время) давало скорость. Наконец, проведя множество наблюдений с использованием различных измерений, можно усреднить неточность полусекундного маятника, давшую окончательную оценку скорости звука. Современные секундомеры позволяют использовать этот метод сегодня на коротких расстояниях от 200 до 400 метров, и при этом не требуется что-то более громкое, чем дробовик.
Методы однократной синхронизации
Самая простая концепция — это измерение, выполняемое с использованием двух микрофонов и устройства быстрой записи, такого как цифровой объем памяти.. В этом методе используется следующая идея.
Если источник звука и два микрофона расположены по прямой линии звука на одном конце, то можно измерить следующее:
- Расстояние между микрофонами (x), называемое основанием микрофона.
- Время прихода между сигналами (задержка), достигающими разных микрофонов (t).
Тогда v = x / t.
Другие методы
В этом методе измерения времени было заменено измерением, обратным времени (частота ).
Трубка Кундта — пример эксперимента, который можно использовать для измерения скорости звука в небольшом объеме. Его преимущество состоит в том, что он может измерять скорость звука в любом газе. В этом методе используется порошок, чтобы сделать узлы и пучности видимыми для человеческих глаз. Это пример компактной экспериментальной установки.
A камертон можно удерживать возле горловины длинной трубы, которая погружается в бочку с водой. В этой системе труба может быть приведена в резонанс, если длина столба воздуха в трубе равна (1 + 2n) λ / 4, где n — целое число. точка антиузла для труб на открытом воздухе находится немного за пределами устья трубы, а затем измерить половину длины волны между ними.
Здесь v = fλ.
Высокоточные измерения в воздухе
Влияние примесей может быть значительным при проведении высокоточных измерений. Химические осушители можно использовать для осушения воздуха, но они, в свою очередь, загрязняют образец. Воздух можно осушить криогенным способом, но это также приведет к удалению углекислого газа; поэтому многие высокоточные измерения выполняются с воздухом, свободным от углекислого газа, а не с естественным воздухом. Обзор 2002 года показал, что измерение Смита и Харлоу в 1963 году с использованием цилиндрического резонатора дало «наиболее вероятное значение стандартной скорости звука на сегодняшний день». Эксперимент проводился с воздухом, из которого был удален углекислый газ, но результат был скорректирован с учетом этого эффекта, чтобы его можно было применить к реальному воздуху. Эксперименты проводились при 30 ° C, но с поправкой на температуру, чтобы сообщить о них при 0 ° C. Результат составил 331,45 ± 0,01 м / с для сухого воздуха в STP для частот от 93 Гц до 1500 Гц.
Негазообразные среды
Скорость звука в твердых телах
Трехмерные твердые тела
В твердом теле имеется ненулевая жесткость как для объемных деформации и деформации сдвига. Следовательно, можно генерировать звуковые волны с разными скоростями в зависимости от режима деформации. Звуковые волны, вызывающие объемные деформации (сжатие) и сдвиговые деформации (сдвиг), называются волнами давления (продольными волнами) и поперечными волнами (поперечными волнами) соответственно. В землетрясениях соответствующие сейсмические волны называются P-волнами (первичными волнами) и S-волнами (вторичными волнами) соответственно. Скорости звука этих двух типов волн, распространяющихся в однородном трехмерном твердом теле, соответственно задаются как
- csolid, p = K + 4 3 G ρ = E (1 — ν) ρ (1 + ν) (1-2 ν), { displaystyle c _ { mathrm {solid, p}} = { sqrt { frac {K + { frac {4} {3}} G} { rho}}} = { sqrt { гидроразрыв { E (1- nu)} { rho (1+ nu) (1-2 nu)}}},}
- csolid, s = G ρ, { displaystyle c _ { mathrm {solid, s}} = { sqrt { frac {G} { rho}}},}
где
- K — модуль объемной упругости упругих материалов;
- G — модуль сдвига упругих материалов;
- E — модуль Юнга; ;
- ρ — плотность;
- ν — Коэффициент Пуассона.
Последняя величина не является независимой, так как E = 3K (1 — 2ν). Обратите внимание, что скорость волн давления зависит как от давления, так и от свойств сопротивления сдвигу материала, в то время как скорость волн зависит от свойств сдвига.
Обычно волны давления распространяются в материалах быстрее, чем поперечные волны, и при землетрясениях это причина того, что начало землетрясения часто предшествует быстрый толчок, направленный вверх-вниз, до прихода волн, которые производят из стороны в сторону. Например, для типичного стального сплава K = 170 ГПа, G = 80 ГПа и ρ = 7700 кг / м, что дает скорость сжатия c твердого тела, p 6000 м / с. Это разумно согласуется с c solid, p, измеренным экспериментально при 5930 м / с для (возможно другого) типа стали. Скорость сдвига c solid, s оценивается в 3200 м / с с использованием тех же чисел.
Одномерные твердые тела
Скорость звука для волн давления в жестких материалах, таких как металлы, иногда указывается для длинных стержней рассматриваемого материала, в скорость легче мера. Величина давления меньше длины волны, скорость чистого давления может быть упрощена и выражена следующим образом:
- csolid = E ρ, { displaystyle c _ { mathrm {solid}} = { sqrt { frac {E } { rho}}},}
где E — модуль Юнга. Это похоже на выражение для поперечных волн, за исключением того, что модуль Юнга заменяет модуль сдвига. Эта скорость звука для волн давления в длинных стержнях всегда будет меньше той же скорости в однородных трехмерных телах, а соотношение скоростей в двух разных типах объектов зависит от коэффициента Пуассона для материала.
Скорость звука в жидкостях
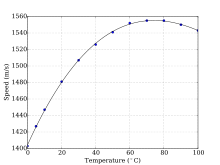
В жидкости единственная ненулевая жесткость Секретари с объемной деформацией (жидкость не выдерживают поперечные силы).
Следовательно, скорость звука в жидкости определяется выражением
- cfluid = K ρ, { displaystyle c _ { mathrm {fluid}} = { sqrt { frac {K} { rho}}},}
где K — модуль объемной упругости жидкости.
Вода
В пресной воде звук распространяется со скоростью около 1481 м / с при 20 ° C (онлайн-калькуляторы см. В разделе «Внешние ссылки» ниже). Применение подводного звука можно найти в гидролокаторе, акустической связи и акустической океанографии.
морской водой

В соленой воде, не содержит пузырьков воздуха или взвешенных отложений, звук распространяется со скоростью около 1500 м / с (1500,235 м / с при 1000 килопаскалей, 10 ° C и 3% солености одним методом). Скорость звука в морской воде зависит от давления (следовательно, глубины), температуры (изменение на 1 ° C ~ 4 м / с) и солености (изменение на 1 ‰ ~ 1 м / с) с), и получены эмпирические уравнения для точного расчета скорости звука на основе этих чисел. Другие факторы, влияющие на скорость звука, незначительны. В качестве отрицательной температуры указывается, что отрицательная температура уменьшается, профиль скорости звука с глубиной уменьшается до минимума на несколько сотен метров. Ниже минимума скорость звука снова увеличивается, поскольку эффект увеличения давления преодолевает эффект снижения температуры (справа). Для получения дополнительной информации см. Dushaw et al.
Маккензи предоставил эмпирическое уравнение для скорости звука в морской воде:
- c (T, S, z) = a 1 + a 2 T + a 3 T 2 + a 4 T 3 + a 5 (S — 35) + a 6 z + a 7 z 2 + a 8 T (S — 35) + a 9 T z 3, { displaystyle c (T, S, z) = a_ {1} + a_ {2} T + a_ {3} T ^ {2} + a_ {4} T ^ {3} + a_ {5} (S-35) + a_ {6} z + a_ {7} z ^ {2} + a_ {8 } T (S-35) + a_ {9} Tz ^ {3},}
где
- T — температура в градусах Цельсия;
- S — соленость в частях на тысячу;
- z — глубина в метрах.
Константы a 1, a 2,…, A 9 равны
- a 1 = 1, 448,96, a 2 = 4,591, a 3 = — 5,304 × 10 — 2, a 4 = 2,374 × 10 — 4, a 5 = 1,340, a 6 = 1,630 × 10–2, a 7 = 1,675 × 10–7, a 8 = — 1,025 × 10–2, a 9 = — 7,139 × 10–13, { displaystyle { begin {align} a_ {1} = 1448.96, a_ {2} = 4.591, a_ {3} = — 5.304 times 10 ^ {- 2}, \ a_ {4} = 2.374 times 10 ^ {- 4}, a_ {5} = 1.340, a_ {6} = 1.630 times 10 ^ {- 2 }, \ a_ {7} = 1,675 times 10 ^ {- 7}, a_ {8} = — 1.025 times 10 ^ {- 2}, a_ {9} = — 7,139 times 10 ^ {- 13}, end {align}}}
с контрольным значением 1550,744 м / с для T = 25 ° C, S = 35 частей на тысячу, z = 1000 м. Это уравнение имеет стандартную ошибку 0,070 м / с для солености от 25 до 40 ppt. См. Технические руководства. Скорость звука в морской воде для онлайн-калькулятора.
(Примечание. График зависимости скорости звука от Deep не коррелирует напрямую с формулой МакКензи. Это связано с тем, что температура и соленость различаются на разных глубинах. Когда T и S остаются постоянными, Сама формула всегда увеличивается с глубиной.)
Другие уравнения скорости звука в морской воде точны в широком диапазоне условий, но гораздо сложнее, например, уравнение В.А. Дель Гроссо и Чена. -Уравнение Миллеро-Ли.
Скорость звука в плазме
Скорость звука в плазме для общего случая, когда электроны горячее, чем ионы (но не намного горячее) определяет формулой (см. здесь )
- cs = (γ Z K T e / mi) 1/2 = 90,85 (γ ZT e / μ) 1/2 м / с, { Displaystyle c_ {s} = ( gamma ZkT _ { mathrm {e}} / m _ { mathrm {i}}) ^ {1/2} = 90,85 ( gamma ZT_ {e} / mu) ^ {1/2} ~ mathrm {м / с},}
где
- mi- масса иона ;
- μ — отношение массы иона к протону масса μ = m i/mp;
- Teравна t he температура электрона;
- Z — состояние заряда;
- k — постоянная Больцмана ;
- γ — индекс адиабаты.
В отличие от Они связаны через колеблющееся электрическое поле.
Градиенты
Когда звук равномерно во всех направлениях в трех измерениях, его интенсивность падает пропорционально. обратному квадрату рату расстояния. В океане есть слой, называемый «глубокий канал» или канал SOFAR, который может ограничивать звуковые волны на определенной глубине.
В канале ГНФАР скорость звука ниже, чем в слоях выше и ниже. Подобно тому, как световые волны будут преломляться в направлении области с более высоким показателем , звуковые волны будут преломляться в направлении области, где их скорость уменьшается. В результате звук ограничивается слоем, так же как свет может быть ограничен листом стекла или оптическим волокном. Таким образом, звук по существу ограничен двумя измерениями. В двух измерениях интенсивность падает только обратной величине расстояния. Это позволяет волнам распространяться намного дальше, чем они становятся незаметно слабыми.
Подобный эффект происходит в атмосфере. Проект Могул успешно использовал этот эффект для обнаружения ядерного взрыва на значительном расстоянии.
См. Также
Ссылки
Внешние ссылки
Содержание:
Звук:
Мы живём в мире звуков: слышим голоса людей, пение птиц, звучание музыкальных инструментов, шум леса, гром во время грозы и т. п.
Раздел физики, в котором изучают звуковые явления, называют акустикой.
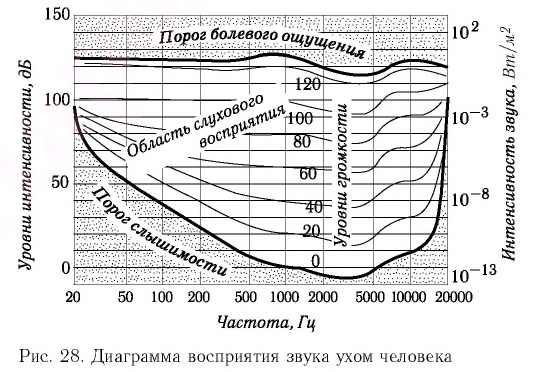
С помощью глаза, воспринимающего свет, мы можем наблюдать волны на поверхности воды как движущиеся последовательные горбы и впадины. Волны, распространяющиеся в газе, внутри жидкости или твердого тела, человек при определённых условиях воспринимает с помощью уха. Ухо человека — прекрасный приёмник звуковых колебаний (рис. 29). Оно состоит из трёх частей: внешнего, среднего и внутреннего уха. Элементами внешнего уха являются ушная раковина 1 и внешний слуховой проход 2. Они служат для того, чтобы направить звуковые волны к барабанной перепонке 4. Барабанная перепонка и соединённые с ней три слуховые косточки — это среднее ухо. Они передают звуковые колебания к элементу внутреннего уха являются: через перепонку овального окна — жидкости, заполняющей улитку 3. Здесь звуковые колебания с помощью слуховых рецепторов превращаются в последовательность нервных импульсов, которые передаются в мозг слуховым нервом.
Опыт 1. Закрепим длинную стальную линейку в тисках или плотно прижмём её к краю стола. Отклоняя свободный конец линейки от положения равновесия, заставим её колебаться (рис. 30). Если линейка довольно длинная, мы ничего не услышим. Укоротим выступающий конец линейки — она начнет «звучать».
Колеблющаяся стальная линейка сжимает слои прилегающего к ней с одной из сторон воздуха и одновременно создаёт разрежение с другой стороны (рис. 31). Эти сжатия и разрежения чередуются во времени и распространяются в обе стороны в виде звуковой волны подобно расходящимся волнам на водной поверхности озера от места, где упал камень. Звуковая волна достигает нашего уха и вызывает колебания барабанной перепонки 4 в среднем ухе.
Человеческое ухо воспринимает в виде звука колебания, частота которых лежит в пределах от 16—17 до 20 ООО Гц. Такие колебания называют звуковыми, или акустическими. В предыдущем опыте мы наблюдали, что чем короче конец линейки, тем выше частота колебаний. Поэтому мы и начинали слышать звук, укоротив конец линейки.
Любое твёрдое, жидкое или газообразное тело, совершающее колебания со звуковой частотой, создаёт в окружающей среде звуковую волну.
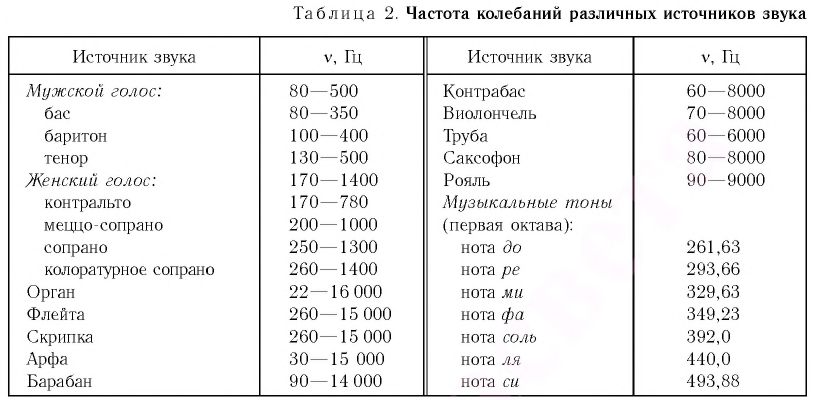
Звуки, которые мы ежедневно слышим, очень разнообразны. Они делятся на музыкальные звуки и шумы. К первым относятся пение, звучание натянутых струн скрипки, гитары или виолончели (рис. 32), духовых или других музыкальных инструментов, свист и т. п.
Шумы возникают во время грозы, создаются работающими двигателями, шелестящей листвой. С помощью органов речи люди могут воссоздавать музыкальные звуки и шумы. Но почему с точки зрения физики музыкальные звуки могут быть такими различными и чем они отличаются от шума ?
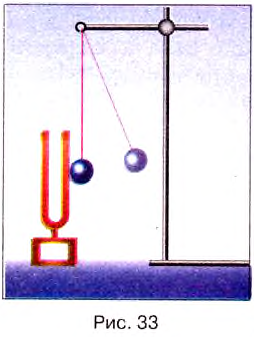
Опыт 2. Возьмём камертон (от немецкого: камм — гребень) и ударим шариком по одной из его ножек (рис. 33).
Мы услышим музыкальный звук «ля» с частотой 440 Гц. Постепенно вследствие затухания колебаний ножек звук слабеет. Итак, звуковая волна возбуждается ножками камертона, совершающими колебания. Характер этих колебаний можно определить, если прикрепить к ножке камертона грифель карандаша и, возбудив колебания камертона, равномерно провести им по поверхности листа бумаги. На бумаге появится волнистая линия (рис. 34), подобная уже знакомой нам синусоиде. В этом случае говорят, что ножки камертона совершают гармонические колебания.
Звук, производимый гармонически колеблющимся телом, называют музыкальным тоном, или тоном.
Музыкальные тоны отличаются на слух громкостью и высотой. Громкость звука зависит от амплитуды колебаний. Чем сильнее удар молоточка по камертону, тем громче он звучит, поскольку сильный удар вызывает колебания большей амплитуды.
Громкость звука зависит от амплитуды колебаний в звуковой волне.
О звуках различной громкости говорят, что один громче другого не во столько -то раз, а на столько-то единиц.
Единицей громкости в СИ является один децибел (1 дБ). Она названа в честь американского учёного Александера Грейама Белла — изобретателя телефона и слуховых аппаратов для глухих.
Громкость звука измеряют специальным прибором — сонометром (рис. 35).
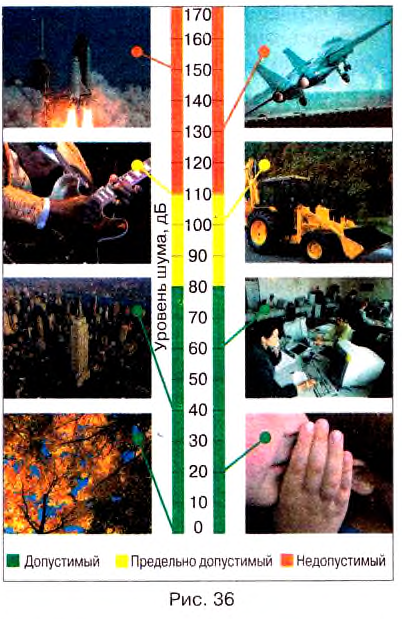
Громкость шелеста листвы составляет 10 дБ, шёпота — 20 дБ, уличного шума — 70 дБ и т. п. (рис. 36)
Чувствительность уха зависит от частоты звука. Звуковые колебания одинаковых амплитуд кажутся неодинаково громкими, если их частоты разные. Человеческое ухо наиболее чувствительно к колебаниям с частотой около 3500 Гц.
Опыт 3. Возьмём несколько камертонов разных размеров. Поочерёдно заставим их звучать и каждый раз грифелем, прикреплённым к ножке камертона, будем проводить вдоль листа бумаги. Сравнивая полученные результаты, увидим, что чем выше звук камертона, тем меньше период колебаний и, соответственно, тем больше частота колебаний ножек камертона.
Высота звука зависит от частоты колебаний.
То же самое можно наблюдать на примере колеблющейся струны. Натягивая сильнее струну гитары или скрипки, мы увеличиваем частоту колебаний, высота звука возрастает.
Звуковые колебания, производимые камертонами (например, у камертона «ля» частота колебаний — 440 Гц) или музыкальными инструментами, можно наблюдать с помощью компьютера или осциллографа (рис. 37 а, б).
А что же такое шум? Шум отличается от музыкального тона тем, что у него нет определённой частоты колебаний, а значит — определённой высоты звука.
Шум- это хаотическая смесь многих звуковых колебаний разных частот и амплитуд.
Какой вид имеют эти колебания, также можно увидеть, используя микрофон и компьютер или осциллограф.
Кстати:
Наиболее «громким» в мире животных является голубой кит. Он может издавать звуки громкостью 188 дБ, которые слышны на расстоянии до 850 км от кита.
Скорость распространения звука
Звуковые волны подобно всем другим волнам распространяются с определённой скоростью.
Наблюдение 1. Каждый замечал, что на поверхности воды в озере от места падения камня с определённой скоростью расходятся волны в виде колец из горбиков и впадин, а через некоторое время они достигают берега и набегают на него. Что же такое волна?
Удар камня возбуждает колебания частичек воды, они передаются соседним участкам жидкости, которые в свою очередь начинают колебаться и передавать колебания дальше.
Механической волной называют распространение колебаний в упругой среде.
За время, равное периоду колебаний Т, горбик волны, двигаясь со скоростью 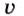
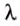
Длина волны — это расстояние, на которое распространяется данное состояние колебания (горбик, впадина) за время, равное периоду колебания.
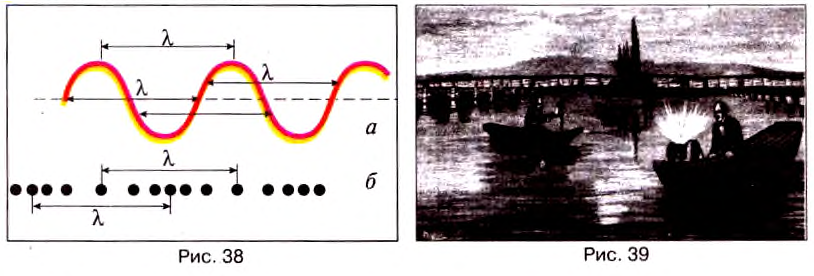
На воде длину волны нетрудно измерить: она равна расстоянию между соседними горбиками или соседними впадинами (рис. 38, а). Чтобы определить скорость распространения волны 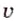
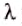
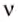
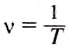
Наблюдение 2. Вы, наверное, замечали, что вспышка молнии предшествует удару грома. Если гроза далеко, то запаздывание грома может достигать десятков секунд. Это запаздывание обусловлено тем, что звуковой волне нужно время, чтобы достигнуть уха от места вспышки молнии.
Звуковая волна — это распространение слоёв сгущённого и разрежённого воздуха, которые чередуются в пространстве и вызываются колебаниями источника, например ножек камертона. На рис. 38, б видно, что длина волны 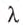
где 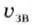
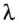
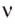
Скорость звука зависит от среды, в которой он распространяется. С помощью опытов Д. Ф. Араго, Прони и Ж. Гей-Люссак в 1822 г. установили, что в воздухе при температуре 10 0С скорость распространения звуковых волн равна 337,2 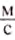
В воде скорость распространения звука больше, чем в воздухе. Впервые её измерили в 1827 г. на Женевском озере в Швейцарии. На одной лодке зажигали порох и синхронно ударяли в подводный колокол (рис. 39). Вторая лодка была на расстоянии 14 км от первой. Звук улавливали с помощью опушенного в воду рупора. По интервалу времени между вспышкой света и поступлением звукового сигнала определили скорость распространения звука. При температуре 8 °С скорость распространения звука в воде равна 1435 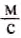
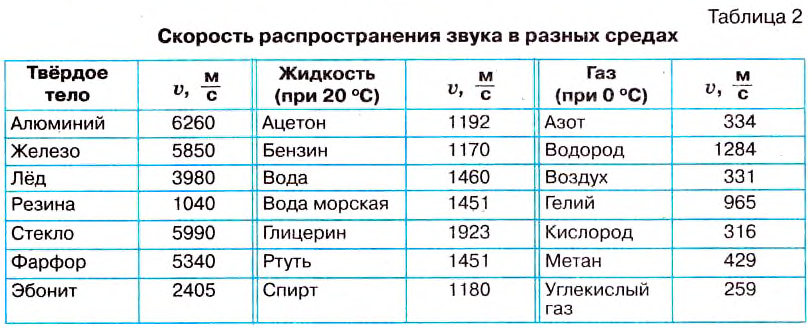
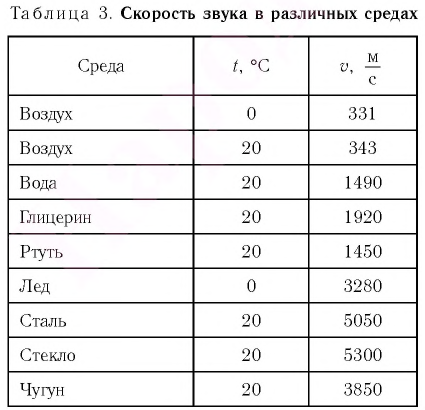
В твёрдых телах скорость распространения звука еще больше, чем в жидкостях. В таблице 2 приведены значения скорости распространения звуковых волн в разных средах.
В таблице 2 указаны значения скорости распространения звука в разных средах при определённой температуре, поскольку скорость распространения звука в среде зависит от её температуры. Например, скорость распространения звука в жидкостях (за исключением воды) с повышением температуры уменьшается, а в газах скорость распространения звука при неизменном давлении с повышением температуры увеличивается.
Современная техника даёт возможность измерить скорость распространения звука с высокой точностью (рис. 40).
Скорость распространения звука в среде зависит от её температуры.
Опыт. Разместим источник звука под колпаком воздушного насоса (рис. 41), и начнём выкачивать из него воздух. По мере того, как количество воздуха под колпаком уменьшается, звук слабеет, а потом вообще исчезает.
Такой опыт впервые выполнил в 1660 г. Роберт Бойль, показав, что в безвоздушном пространстве, которое называют вакуумом, звук совсем не распространяется. Тем самым он доказал необходимость среды для существования звуковых волн. Есть материалы, которые плохо проводят звук, поскольку колебания в них быстро затухают. Например, пористые панели, пенопласт используют для звукоизоляции, т. е. для защиты помещений от проникновения в них посторонних звуков. Если звуковая волна распространяется в некоторой среде (например, воде), то со временем она достигнет её границы, к которой примыкает другая среда (например, воздух).
Эта вторая среда состоит из других частиц и отличается строением, поэтому скорость распространения звука в ней иная. На границе двух различных сред происходит отражение звуковой волны подобно отражению света на границе воздуха и зеркала.
Почему отражается звуковая волна? Происходит это потому, что колебания звуковой волны передаются частицам другой среды. Эти частицы сами становятся источниками новой (вторичной) звуковой волны. Вторичная волна распространяется не только во второй среде, но и в первой, откуда поступила первичная волна. Это и есть отражённая волна.
С отражением звука связано известное всем явление — эхо. Оно заключается в том, что звук от источника доходит до некоторого препятствия (а препятствием и есть вторая, отличная от воздуха среда — стена дома, край леса и т. п.), отражается от его поверхности и возвращается к месту, где возникли звуковые колебания.
Если первичный звук и звук отражённый доходят к слушателю не одновременно, то он слышит звук дважды. Бывают случаи многократных отражений звука, тогда и услышать его можно несколько раз (например, раскаты грома).
Явление отражения звуковых волн от препятствий используют для определения расстояний до разных предметов и их местонахождения. Предположим, что в определённый момент времени источник звука создаёт звуковые колебания. Звук распространяется, и, встретив препятствие, отражается от него. Если возле источника звука разместить ещё и приемник, то через определённый интервал времени он может зафиксировать отражённый звук. Измерив этот интервал времени и зная скорость распространения звука в данной среде, определяют расстояние до препятствия, учитывая, что звук дважды проходит искомое расстояние (до препятствия и обратно) по формуле:
где 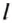
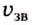
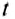
Инфразвук и ультразвук
Вы уже знаете, что колебания с частотой от 16 до 20 ООО Гц воспринимает человеческое ухо, поэтому их называют звуковыми.
Колебания с частотами, которые меньше чем наинизшая звуковая частота называют инфразвуком (от латинского слова инфра — ниже, под).
Инфразвуковые колебания (инфразвук) — это колебания, частота которых меньше 16 Гц — самой низкой частоты звуковых колебаний.
Человеческое ухо инфразвук не воспринимает. Он возникает во время штормов, гроз, землетрясений. Человеческий организм в целом ощущает на себе вредное действие инфразвука, человек очень страдает от морской и воздушной болезней, возникающих вследствие укачивания в инфразвуковом диапазоне колебаний. Медицинские исследования влияния на человека продолжительного воздействия инфразвука от специальных генераторов свидетельствуют, что оно может привести к непоправимым последствиям.
Инфразвук слабо поглощается средой и может распространяться на большие расстояния. Инфразвук используют в приборах, которые называют сейсмографами. Они предназначены для прогнозирования землетрясений, изучения строения Земли, разведки полезных ископаемых (рис. 42).
Колебания с частотами, которые больше, чем наивысшая звуковая частота, называют ультразвуком (от латинского слова ультра — дальше, больше, над). Ультразвуковые колебания (ультразвук) — это колебания, частота которых больше 20 ООО Гц — самой высокой частоты звуковых колебаний.
Ультразвуковые колебания применяют для обработки твёрдых и сверхтвердых материалов. К обрабатываемым деталям подаётся смесь воды с мелким порошком-абразивом, частички которого под действием ультразвукового излучателя колеблются с большой частотой, бомбардируя обрабатываемую поверхность, благодаря чему в ней можно делать отверстия сложной формы. Так получают изображения на камне, металле, фарфоре и т. п.
Мы уже знаем, что с помощью звукового эха можно определить расстояние до препятствия, на практике также нужно знать, в каком направлении оно расположено. Обычный звук для этого непригоден, поскольку он распространяется по всем направлениям от источника, поэтому и отражённые сигналы поступают с разных сторон.
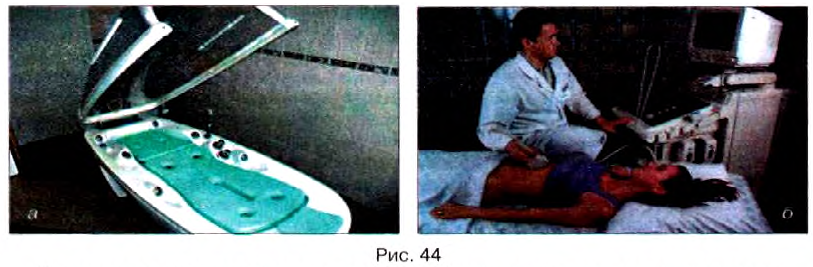
С целью определения местонахождения объектов методом эха используют не обычный звук, а ультразвук. Он имеет значительно высшую частоту колебаний, чем звук, т. е. очень малую длину волны, что даёт возможность сформировать узкие ультразвуковые пучки, подобные световым, и определить кроме расстояния до объекта ещё и направление на него.
Этот принцип положен в основу действия эхолота и эхолокатора — приборов для измерения глубины морей, океанов или поиска различных предметов под водой. На днищах судов устанавливают ультразвуковые излучатели, которые периодически посылают импульсы в направлении дна (рис. 43, а). Отражённые колебания принимаются (рис. 43, б), и на экране компьютера появляется рельеф дна. Когда на пути ультразвука возникает, например, косяк рыбы, он также отображается на экране. Для многих технических целей нужны смеси жидкостей, которые не смешиваются в обычных условиях (например, ртуть и вода). Но если колбу с водой и ртутью облучать на протяжении определенного времени ультразвуком, то образуется устойчивая смесь, которая может сохраняться в течение продолжительного времени. На промышленных предприятиях с помощью ультразвуковых колебаний смешивают воду и масло.
Учёные установили, что простейшие живые существа быстро гибнут под действием ультразвука. Это свойство используют для стерилизации воды, молока и других пищевых продуктов. Ультразвук является причиной паралича и гибели холоднокровных животных — рыб, жаб. головастиков.
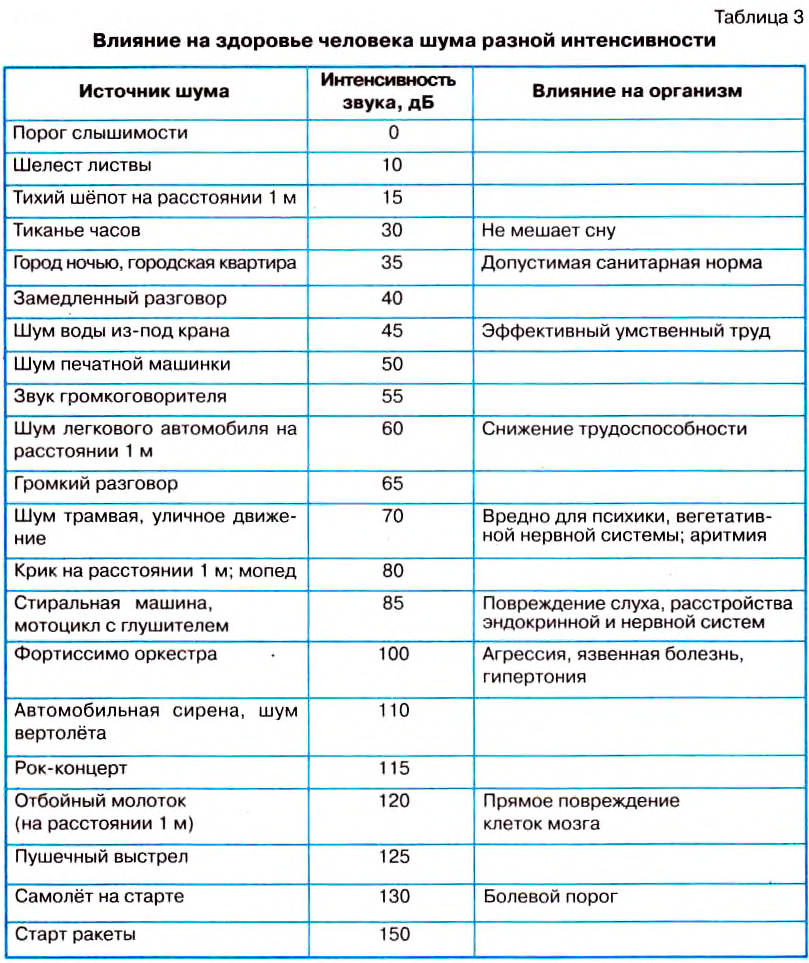
В медицине ультразвук используют с лечебной (рис. 44, а) и диагностической целями (рис. 44. б).
Кстати:
Свыше 80 лет тому назад французский ученый Поль Ланжевен получил патент на первый в мире ультразвуковой локатор. Но природа опередила его лучшие мыши и китообразные, ориентируясь в пространстве, действуют как живые эхолокаторы, так как способны излучать и воспринимать ультразвук в широком диапазоне. Дельфин четко отличает скалу от косяка рыб. Собаки слышат ультразвук, поэтому им можно подавать неслышные для людей команды с помощью специальных свистков.
Влияние акустических колебаний на живые организмы
Среди физических факторов, отрицательно влияющих на здоровье человека, одним из наиболее вредных является звуковой шум. Он воспринимается как неприятные, нежелательные звуки, мешающие нормально работать, получать нужную информацию, отдыхать. Учёные установили, что шум даже малой интенсивности приводит к снижению трудоспособности, остроты слуха, изменению функциональных возможностей коры главного мозга, сердечно-сосудистой и центральной нервной систем. Шум действует на человека возбуждающе, вызывает выделение в кровь большого количества гормонов, вызывающих чувство страха, опасности, агрессии и т. п.
Шум — сложное физическое явление: он образуется вследствие наложения колебаний различных частот, то есть состоит из звуков разной высоты. Он является одной из форм физического (волнового) загрязнения окружающей среды, адаптация организмов к которому практически невозможна. Поэтому шум относится к серьёзным загрязнителям, которые должны быть под контролем государства на основе специальных законов.
Правовую основу защиты населения от шума представляют Законы Украины «Об обеспечении санитарного и эпидемического благополучия населения», «Об охране естественной окружающей среды», «Об охране атмосферного воздуха», «Об экологической экспертизе» и др.
Борьба с шумом состоит в создании шумоулавливаюших экранов, поглощающих фильтров, бесшумных механизмов, в изменении технологии производства и динамики транспортных потоков. Даже озеленение территории снижает уличный шум на 25 % и более.
Уровень шума, его сила (интенсивность) измеряется в децибелах (дБ). Интенсивность всех звуков диапазона слухового восприятия выражают в относительных единицах от 0 до 130 дБ (болевого порога). Измеряют шум специальной аппаратурой — шумомерами.
Допустимые границы силы звука в разных условиях составляют 45—85 дБ. В случае постоянного шума до 70 дБ возникают нарушения эндокринной и нервной систем, при 90 дБ нарушается слух, при 120 дБ возникает физическая боль, становящаяся невыносимой.
Рекомендованные диапазоны шумов внутри помещений разного назначения такие:
- •для сна, отдыха — 30—40 дБ;
- •для умственного труда — 40—50 дБ;
- •для лабораторных исследований, работы с ЭВМ и т. п. — 50—60 дБ;
- •для производственных цехов, гаражей, магазинов и т. п. — 50—70 дБ.
Источниками шумов являются все виды транспорта, промышленные объекты, громкоговорящие устройства, лифты, телевизоры, радиоприёмники, музыкальные инструменты, собрания людей и отдельные лица (табл. 3). Чрезмерный шум влияет на организм человека подобно яду, который в организме медленно накапливается. Он сокращает продолжительность жизни на 8-12 лет.
Медицинские исследования свидетельствуют, что у лиц, имеющих «шумные» профессии, желудочные заболевания (гастриты, язвы и т. п.) возникают в четыре раза чаще, чем у других. Среди них также намного больше глухих. От продолжительного сильного шума производительность у людей умственного труда снижается на 60 %, физического — на 30 %.
Оказалось, что молодежь до 27 лет выдерживает намного более интенсивный шум, чем люди возрастом более 40—50 лет. Однако со временем, как свидетельствует статистика, у молодых людей, увлекающихся громкой музыкой (на концертах и дома), после 30 лет возникают расстройства слуха, нервной системы и другие болезни.
Наблюдение специалистов свидетельствуют, что в концертных залах, где выступают современные рок-ансамбли, в первых рядах интенсивность звука достигает 118—120 дБ, в последних — 100—110 дБ. Врачи считают, что после каждого такого концерта почти у 10 % слушателей возникают необратимые повреждения внутреннего уха (нервных окончаний), которые не восстанавливаются. Установлено, что очень громкая музыка негативно влияет на вегетативную нервную систему человека, сердце, кровообращение, органы дыхания.
Положительное влияние гармонической, спокойной, мягкой музыки было известно с давних времён. Существует так называемая музыкальная терапия, когда различные оздоровительные процедуры сопровождаются нежными монотонными напевами, спокойным журчаньем воды, мягким шумом морских волн, птичьим пением, спокойной симфонической музыкой.
- Заказать решение задач по физике
Пример №1
Услышим ли взрыв, который произошёл на Луне?
Ответ: нет, так как на Луне отсутствует атмосфера. Звук в безвоздушном пространстве не распространяется.
Пример №2
Выпишите названия музыкальных инструментов в порядке возрастания высоты тона (в скобках указана частота звуковых колебаний): скрипка (640 Гц), виолончель (216 Гц), контрабас (196 Гц), альт (415 Гц).
Ответ: контрабас (196 Гц), виолончель (216 Гц), альт (415 Гц), скрипка (640 Гц).
Пример №3
Эхо услышали через 2 с после вскрика мальчика перед лесом. На каком расстоянии от леса был мальчик?
Дано:
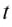
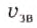
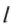
Решение:
Используем формулу:
Подставим значения: 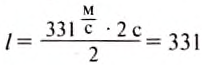
Ответ: 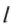
Что такое звук
Особенно важное место среди всех типов упругих волн занимают звуковые волны (звуки). Мир окружающих нас звуков разнообразен и сложен, однако мы достаточно легко ориентируемся в нем и можем безошибочно отличить пение птиц от шума городской улицы.
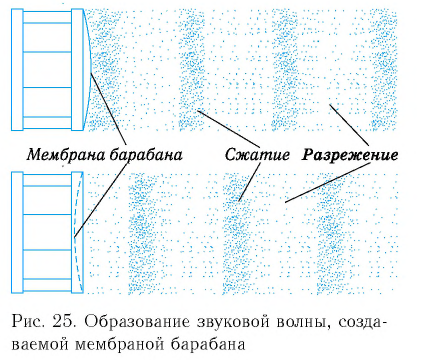
Рассмотрим в качестве примера источника звука барабан (рис. 25).
Мембрана барабана создает попеременно сжатие и разрежение в прилегающей к ней области воздуха, и образуется продольная волна, которая распространяется в воздухе. Графически ее можно представить как зависимость плотности молекул воздуха от координаты (рис. 26).
Таким образом, в процессе распространения звуковой волны с течением времени изменяются такие характеристики среды, как плотность и давление.
Для распространения звуковых волн необходимы среды с упругими свойствами.
Если поместить источник звука (звонок) под колокол воздушного насоса и постепенно откачивать воздух, то звук становится все слабее и слабее, а затем исчезает. Следовательно, звуковые волны в безвоздушном пространстве не распространяются.
Если окружить звонок слоем пористого материала (поролона, ваты, войлока и т. п.), то звуковые волны в нем быстро затухают. Поэтому такие материалы широко используются для звукоизоляции.
Упругие волны, вызывающие у человека слуховые ощущения, называются звуковыми волнами или просто звуком. Человеческое ухо воспринимает звук в частотном диапазоне от 16 до 20 ООО Гц.
Раздел физики, В котором изучаются звуковые явления называется акустикой.
Звуковые волны классифицируются по частоте следующим образом. ( рис 27):
Многие животные могут воспринимать ультразвуки. Например, собаки могут слышать звуки частотой до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
Основными физическими характеристиками звука являются интенсивность и спектральный состав (спектр).
Для характеристики энергии, переносимой волнами, используется понятие интенсивности волны 
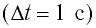
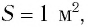
Другими словами, интенсивность представляет собой мощность 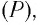
Единицей интенсивности в СИ является 1 ватт на метр в квадрате
Уровень интенсивности звука 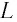
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.
Интенсивность звука, улавливаемого ухом человека, лежит в очень широких пределах: от 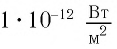
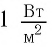
Минимальная интенсивность, при которой ухо человека перестает воспринимать звук, называется порогом слышимости. Кривая порога слышимости для всего звукового диапазона приведена на рисунке 28 (в логарифмическом
масштабе). Наиболее чувствительно наше ухо к волнам частотой примерно 3 кГц, так как интенсивности порядка 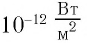
При значительной интенсивности колебаний ухо перестает воспринимать колебания как звук, испытывая при этом болевое ощущение. Такая интенсивность, выше которой отмечается боль, называется порогом болевого ощущения. Порог болевого ощущения соответствует интенсивности, равной примерно 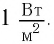
Реактивный самолет может создать звук интенсивностью порядка 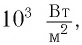
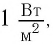
В технике предпочитают измерять изменение интенсивности звука не по изменению энергии волны (на диаграмме справа), а в других единицах — децибелах (на диаграмме слева).
Таким образом, для возникновения звуковых ощущений необходимо: наличие источника звука;
наличие упругой среды между источником звука и ухом; частота колебаний источника звука должна находиться в пределах 16—20 000 Гц; мощность звуковых волн должна быть достаточной для того, чтобы вызывать ощущение звука.
Спектром называется набор звуков различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.
Сплошной спектр означает, что в данном наборе присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.
Дискретный спектр означает наличие конечного числа волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал. По типу спектра звуки разделяются на шумы и музыкальные тоны.
Шум — совокупность разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т. п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).
Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию на различных музыкальных инструментах. Интервал частот музыкальных звуков, на границах которого звуки по частоте отличаются в 2 раза, называют октавой.
Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.
Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это обусловлено тем, что восприятие звука — процесс не только физический, но и физиологический. Человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).
Основными физиологическими характеристиками звука являются громкость, высота и тембр.
Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1 ООО до 5000 Гц.
С возрастом порог слышимости человека возрастает. Следует отметить, что болевой порог изменяется в зависимости от часто™ не столь существенно, как порог слышимости.
При увеличении интенсивности в 10 раз уровень громкости увеличивается на 20 дБ. Вследствие этого звук в 50 дБ оказывается в 100 раз интенсивнее звука в 30 дБ.
Высота звука определяется частотой звуковых колебаний, обладающих наибольшей интенсивностью в спектре.
Тембр (оттенок звука) зависит от того, сколько обертонов присоединяются к основному тону и какова их интенсивность и частота. По тембру мы легко отличаем звуки скрипки и рояля, флейты и гитары, голоса людей (табл. 2) и т. д.
Модуль скорости звука зависит от упругих свойств, плотности и температуры среды. Чем больше упругие силы, тем быстрее передаются колебания частиц соседним частицам и тем быстрее распространяется волна. Поэтому модуль скорости звука в газах меньше, чем в жидкостях, а в жидкостях, как правило, меньше, чем в твердых телах (табл. 3).
Модуль скорости звука в идеальных газах с ростом температуры растет пропорционально 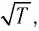
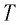
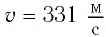
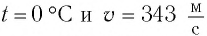
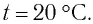
Впервые модуль скорости звука в воздухе был определен в 1640 г. французским физиком Мареном Мерсенном. Он измерял промежуток времени между моментами появления вспышки и звука при ружейном выстреле. Мерсенн определил, что модуль скорости звука в воздухе равен
Способ ориентации или исследования окружающих объектов, основанный на излучении ультразвуковых импульсов с последующим восприятием отраженных импульсов (эха) от различных объектов, называется эхолокацией, а соответствующие приборы — эхолокаторами.
Эхолокацию используют различные китообразные (дельфины), а также летучие мыши, птицы гуахаро, гнездящиеся в глубоких пещерах Венесуэлы и на острове Тринидад, стрижи-салаганы, живущие в пещерах Юго-Восточной Азии. Волны ультразвуковых частот широко используются в медицине в диагностических целях. УЗИ-сканеры позволяют исследовать внутренние органы человека.
Пример №4
Стальные детали проверяются ультразвуковым дефектоскопом. Определите толщину 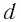
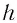
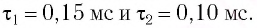
Дано:
Решение
Так как сигнал проходит деталь туда и обратно, то толщину детали определим по формуле:
Аналогично определяется глубина, на которой находится дефект:
Ответ:
Итоги:
Периодическим называется движение, при котором физические величины, характеризующие колебательную систему, через равные промежутки времени принимают одинаковые значения.
Колебательным называется движение (процесс), при котором любая характеризующая это движение (процесс) физическая величина поочередно изменяется то в одну, то в другую сторону от ее значения в положении устойчивого равновесия.
Периодическим колебательным движением (колебаниями) называют любой процесс, который обладает свойством повторяемости во времени. Колебания любой физической природы, описываемые уравнением
являются гармоническими, а система, совершающая такие колебания, — гармонической колебательной системой, или гармоническим осциллятором.
Колебания, при которых зависимость координаты (смещения) тела от времени определяется соотношениями
или
называются гармоническими.
Зависимость координаты от времени 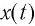
Колебания материальной точки являются гармоническими, если они происходят под действием возвращающей силы, модуль которой прямо пропорционален смещению точки из положения равновесия 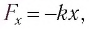
Амплитуда колебаний 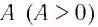
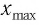
Фаза колебаний 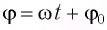
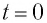
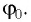
Циклическая частота 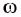
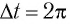
Период колебания 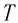
Частота колебаний 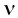
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Его период колебаний:
Колебательная система, состоящая из небольшого тела, подвешенного на легкой нерастяжимой нити, называется математическим маятником.
Период малых колебаний математического маятника определяется по формуле Гюйгенса:
Собственные (свободные) колебания — это колебания, происходящие в отсутствие внешних воздействий на систему. Они происходят со строго определенной частотой, называемой частотой собственных колебаний системы.
Затухающими называются колебания, энергия которых уменьшается с течением времени.
Вынужденными называются колебания системы, вызываемые действием на нее периодических внешних сил.
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний, когда частота периодической внешней силы совпадает с собственной частотой колебаний системы.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Длина волны — расстояние, пройденное волной в среде за промежуток времени, равный периоду колебаний частиц:
Скорость распространения волны — это скорость распространения гребня волны или любой другой точки волны с определенной фазой, модуль которой
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волны.
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны.
Упругие волны, вызывающие у человека слуховые ощущения, называются звуковыми волнами или просто звуком.
Основными физическими характеристиками звука являются интенсивность и спектральный состав (спектр).
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Масса тела в физике
- Сила в физике
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
- Линзы в физике
- Глаз как оптическая система
В опытах с резиновым шнуром и шариками, соединенными пружиной, мы наблюдали волны, которые распространялись только в одну сторону. В сплошных средах волны распространяются по всем направлениям. Сплошной средой можно считать любую жидкость, газ или твердой тело, которые сплошь заполняют некоторую область пространства.
В сплошной среде волны всегда являются затухающими. Это связано с тем, что при колебательном движении между частицами возникают силы трения. Поэтому полная механическая энергия колеблющихся частиц уменьшается. Вспомним, что полная механическая энергия колеблющегося тела равна:
W=kx2max2
где xmax — амплитуда колебаний, а k — коэффициент упругости.
Поскольку часть энергии уходит на преодолении сил трения, со временем она уменьшается. Следовательно, уменьшается и амплитуда колебаний частиц. Исключение составляют плоские волны, амплитуда колебаний которых остается постоянной (или почти постоянной).
Плоские волны
Определение
Плоская волна — волна, образованная бесконечно большой плоской пластиной, колеблющейся перпендикулярно к ее нормали в сплошной среде.
Все частицы, лежащие в одной плоскости, параллельной пластине, колеблются в одной фазе. Поверхности равной фазы называются волновыми поверхностями. А линию, перпендикулярную такой поверхности, называют лучом. Под направлением распространения волн понимают направление лучей.
Волновые поверхности плоской волны представляют собой плоскости, параллельные колеблющейся пластине.
При распространении плоской волны размеры волновых поверхностей по мере удаления от пластины не меняются (или почти не меняются). Поэтому энергия волны не рассеивается в пространстве, и амплитуда колебаний уменьшается только за счет действия сил трения.
Сферические волны
Другой пример волны в среде — сферическая волна. Сферическая волна возникает, если в среду поместить пульсирующую сферу. В этом случае волновые поверхности представляют собой сферы. Лучи же направляются вдоль продолжений радиусов пульсирующей сферы (см. рисунок).
Амплитуда колебаний частиц в случае сферической волны обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, в этом случае равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны.
Площадь поверхности сферы пропорциональна квадрату радиуса:
S=4πr2
Следовательно, энергия, переносимая волной, убывает обратно пропорционально квадрату расстояния от источника:
W~1r2
Амплитуда же колебаний, квадрат которой пропорционален энергии, убывает обратно пропорционально первой степени расстояния от источника:
smax~1r
Пример №1. Найти расстояние между точками пространства 1 и 2, если известно, что в точке 1 энергия волны равна 10 Дж, а в точке 2— 6 Дж. Считать, что в среде нет трения.
Поскольку энергия волны убывает обратно пропорционально квадрату расстояния от источника, примем, что разность энергий волны в точках 1 и 2 обратно пропорциональна квадрату расстояния между ними:
(W1−W2)~1r2
(10−6)~1r2
4~1r2
Тогда:
r~√14~12 (м)
Поперечные и продольные волны в средах
Как вы знаете, волны могут быть поперечными и продольными. В поперечной волне смещения отдельных участков среды происходят в направлении, перпендикулярном распространению волны. При этом происходит упругая деформация, называемая деформацией сдвига. Отдельные слои вещества сдвигаются друг относительно друга. Объем тела не изменяется. При деформации сдвига в твердом теле возникают силы упругости, стремящиеся вернуть тело в исходное состояние. Именно эти силы и вызывают колебания среды.
Сдвиг слоев друг относительно друга в газах и жидкостях не приводит к появлению сил упругости. Поэтому в газах и жидкостях не могут существовать поперечные волны. Поперечные волны возникают только в твердых телах.
Внимание!
Исключение составляют поверхности жидкостей, в которых могут возникать поперечные волны за счет сил поверхностного натяжения. Но внутри жидкостей могут распространяться только продольные волны.
В продольной волне происходит деформация сжатия и растяжения. Силы упругости, связанные с этой деформацией, возникают как в твердых телах, так и в жидкостях и газах. Эти силы вызывают колебания отдельных участков среды, поэтому продольные волны могут распространяться во всех средах.
Это интересно!
В твердых средах скорость продольных волн больше скорости поперечных волн. Зная скорости продольных и поперечных волн в земной коре, а также время запаздывания поперечной волны, можно определить расстояние до очага землетрясения.
Звуковые волны
Волны на поверхности воды или волны вдоль резинового шнура можно непосредственно видеть. В прозрачной среде — воздухе или жидкости — волны невидимы. Но при определенных условиях их можно слышать.
Зажмем в тиски металлическую линейку и отклоним ее верхнюю часть в сторону, затем отпустим. Линейка начнет совершать колебательные движения. Мы их увидим, но не услышим.
Теперь проделаем тот же самый опыт, но укоротим линейку. Теперь мы сможем не только видеть, но и слышать колебания.
Почему одни колебания можно услышать, а другие нет? Все дело в частоте колебаний. В опытах линейка совершала колебания разных частот. Известно, что период колебаний зависит от длины колеблющегося тела. Он пропорционален корню из этой длины:
T~√l
Следовательно, когда длина линейки меньше, период колебаний тоже меньше. Также известно, что период представляет собой величину, обратную частоте:
T=1ν
Следовательно, если период колебаний меньше, то частоты выше. Ухо человека воспринимает колебания сплошных сред как звук, если их частота находится в диапазоне от 16 до 20 000 Гц.
Это интересно!
Колебания частотой до 16 Гц называют инфразвуком, а колебания частотой более 20 000 Гц — ультразвуком. Ультразвук могут слышать многие животные. К примеру, кошки воспринимают звуки частотой от 45 до 64 000 Гц.
Пример №2. Сильный ветер раскачивает ствол дерева так, что он совершает одно колебание за 2 секунды. Определить, услышит ли человек звук раскачивающегося ствола дерева.
Чтобы дать ответ на вопрос, нужно найти частоту колебаний дерева:
ν=1T=12 (Гц)
Теперь сравним полученное значение с частотами, которые может слышать человек. Минимальная частота, воспринимаемая человеческим ухом, составляет 16 Гц. 1/2 меньше 16. Следовательно, звук колебаний ствола дерева человек не услышит.
Как возбуждаются звуковые волны
Как же получается, что мы можем слышать звук колеблющегося конца линейки? Дело в том, что когда линейка отклоняется, она толкает воздух впереди себя, создавая уплотнение. С обратной же стороны образуется разрешение. То есть, колеблющаяся линейка порождает продольную волну.
Так как воздух — сплошная среда, то волна распространяется во все стороны. Она состоит из чередующихся зон повышенной и пониженной плотности (см. рисунок ниже). Плотные участки воздуха давят на барабанную перепонку уха. Так волна становится слышимой.
Звук может распространяться в любой среде: жидкой, газообразной и твердой. Причем чем плотнее среда, тем быстрее распространяется звук. Так, быстрее всего звуковая волна распространяется в твердых телах, чуть медленнее — в жидкостях. Медленнее всего она распространяется в воздухе. В вакууме звук услышать нельзя. Звук представляет собой продольную волну в сплошной вещественной среде. В вакууме вещества нет (или почти нет).
Это интересно!
Распространяясь, амплитуда звуковых волн уменьшается. Часть энергии волн также теряется при переходе из газообразной среды в твердую среду. Поэтому для защиты помещений от посторонних звуков люди применяют войлок, пробку, ворсистые ковры и другие пористые материалы.
Скорость звука
Звуковые волны, подобно всем другим волнам, распространяются с конечной скоростью. Обнаружить это можно так. Свет распространяется с огромной скоростью — 300 000 км/с. Поэтому вспышка от выстрела почти мгновенно достигает глаз. Звук же выстрела приходит с заметным запаздыванием. То же самое можно заметить, наблюдая с большого расстояния игру в футбол. Вы видите удар по мячу, а звук от удара приходит спустя некоторое время. Все, вероятно, замечали, что вспышка молнии предшествует раскату грома. Если гроза далеко, то запаздывание грома достигает нескольких десятков секунд. Наконец, из-за конечной скорости звука появляется эхо. Эхо — это звуковая волна, отраженная от опушки леса, крутого берега, здания и т. д.
Чтобы вычислить скорость звука, нужно знать расстояние от источника звука до слушателя, а также разницу времени между тем, как звук был издан, и тем, как он был услышан. В таком случае скорость можно будет вычислить по формуле:
v=st
Так как звук — это волна, то скорость звука является скорость распространения волны, которая равна отношению длины волны к периоду колебаний:
v=λT
Приведем в таблице приблизительные скорости звука в различных средах.
Пример №3. Определите скорость звука в воде, если колебания с периодом T = 0,005 с, порождают звуковую волну длиной λ = 7,175 м.
v=λT=7,175 0,005=1435 (мс)
Эхо
Определение
Эхо — отраженная от препятствия звуковая волна.
Звуковые волны, распространяющихся в неплотных средах (например, в воздухе), имеют способность отражаться от более плотных сред (твердых тел) в направлении к источнику звука. Эхо можно услышать в горах, в лесу, в большом пустом помещении, но его нельзя услышать в маленькой комнате. С чес же это связано?
Человеческое ухо воспринимает одинаковые звуки как два отдельных звука только в случае, если временной между ними составляет не менее 0,06 с. Если отраженная звуковая волна достигла уха раньше, чем за это время, мозг объединит эти звуки в один. Чем меньше расстояние от источника звука до препятствия, тем быстрее приходит эхо.
Пример №4. Это, вызванное ружейным выстрелом, дошло до стрелка через 4 с после выстрела. На каком расстоянии от наблюдателя находится преграда, от которой произошло отражение звука? Считать, что скорость звука в воздухе равна 330 м/с.
Звуковая волна прошла двойное расстояние от стрелка до препятствия: сначала от наблюдателя к этому препятствию, затем от препятствия к этому наблюдателю. Следовательно, найти его можно по следующей формуле:
2s=vt
s=vt2=330·42=660 (м)
Задание EF19116
Какова глубина вертикальной шахты, если звук выстрела, произведённого у входа в шахту на поверхности земли, вернулся к стрелку, отразившись от дна шахты, через 0,5с после выстрела? Скорость звука в воздухе считать равной 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Промежуток времени между выстрелом и эхом: t = 0,5 с.
Звук от выстрела проделает путь, равный двойному расстоянию от стрелка до дна шахты. Сначала он достигнет дна шахты, затем вернется к стрелку. Поскольку скорость звука постоянна, для преодоления половины пути потребуется вдвое меньше времени. Следовательно, для нахождения времени между выстрелом и эхо нужно умножить скорость звука в воздухе на половину промежутка времени между выстрелом и эхом:
s=vt2=340·0,52=85 (м)
Ответ: 85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22741
Колеблющаяся струна издаёт звук с длиной волны 0,68 м. Какова частота её колебаний, если скорость звука в воздухе 340 м/с?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает длину волны с ее частотой.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Длина волны: λ = 0,68 м.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν
Отсюда:
ν=vλ=3400,68=500 (Гц)
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18740
Через какое время после выстрела придёт к охотнику эхо от звука выстрела, если расстояние до преграды, от которой отразится звук, равно 850 м? Скорость звука в воздухе считать равной 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
- Скорость распространения звука в воздухе: v = 340 м/с.
- Расстояние до преграды: s = 850 м.
Звук от выстрела проделает путь, равный двойному расстоянию от охотника до преграды. Сначала он достигнет преграды, затем вернется к охотнику. Следовательно, для нахождения времени между выстрелом и эхо нужно разделить этот путь на скорость звука в воздухе:
t=2sv=2·850340=5 (с)
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 2.9k
Скорость звука в жидкостях, формула
Если:
c — Скорость звука в жидкости (м/с),
K = 1/χ — Модуль всестороннего сжатия (Н/м²),
χ — коэффициент сжимаемости жидкости (м²/Н),
ρ — Плотность жидкости (кг/м³),
То, Скорость звука в жидкости описывается следующей формулой:
[ c = sqrt{frac{K}{ρ}} = sqrt{frac{1}{χρ}} ]
Поскольку скорость звука c выражается через плотность ρ, то она зависит от температуры.
Вычислить, найти скорость звука в жидкостях по формуле (1) через K
Вычислить, найти скорость звука в жидкостях по формуле (1) через χ
Скорость звука в жидкостях |
стр. 581 |
|---|


 — это плотность.
— это плотность.







 ) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;
) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;