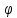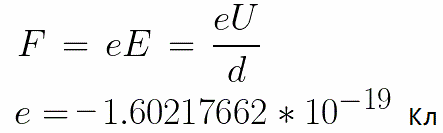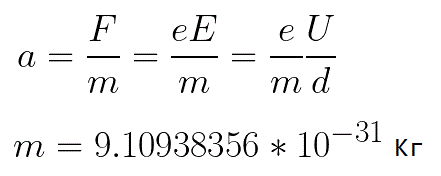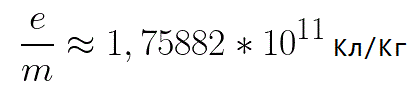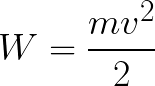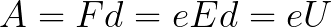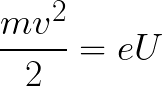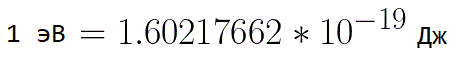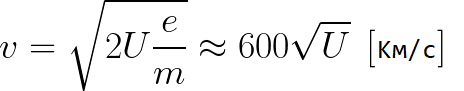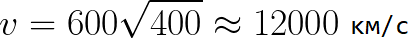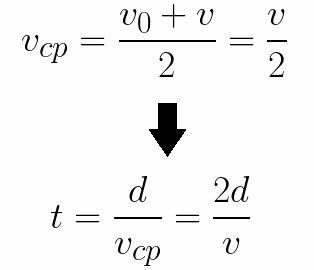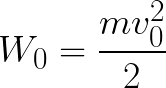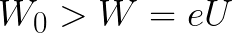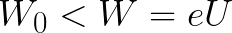$begingroup$
I have this homework question and I get a different answer to the solutions.
In Cylindrical polar coordinates $(r,theta,z)$, the velocity potential of a flow is given by:
$$phi = -frac{Ua^2r}{b^2-a^2}(1+frac{b^2}{r^2})costheta$$
Find the velocity.
I get the velocity as:
$$v = (-frac{Ua^2}{b^2-a^2}(1+frac{b^2}{r^2})costheta + frac{2Ua^2b^2}{(b^2-a^2)r^2}costheta)e_r + (frac{Ua^2}{b^2-a^2}(1+frac{b^2}{r^2})sintheta) e_{theta}$$
The answer misses out the second term in the $r$ direction, but I can’t see where I’ve gone wrong. Any help appreciated.
OSE
1,49512 silver badges27 bronze badges
asked Oct 6, 2013 at 16:36
$endgroup$
0
$begingroup$
For a flow in polar coordinates, the stream function $phi$ leads to the velocities as
$$
v_r=frac{1}{r}frac{partialphi}{partialtheta}qquad v_theta=-frac{partialphi}{partial r}
$$
and not $v_r=partial_rphi$ and $v_theta=partial_thetaphi$. Thus,
$$
v_r=frac{1}{r}frac{partial}{partial theta}left(-frac{Ua^2r}{b^2-a^2}left(1+frac{b^2}{r^2}right)costhetaright) \
= frac{1}{r}left(frac{Ua^2r}{b^2-a^2}left(1+frac{b^2}{r^2}right)sinthetaright) \
=frac{Ua^2}{b^2-a^2}left(1+frac{b^2}{r^2}right)sintheta
$$
and
$$
v_theta=-frac{partial}{partial r}left(-frac{Ua^2r}{b^2-a^2}costheta-frac{Ua^2}{b^2-a^2}frac{b^2}{r}costhetaright) \
= +frac{Ua^2}{b^2-a^2}costheta-frac{Ua^2}{b^2-a^2}frac{b^2}{r^2}costheta
$$
If $v_0equiv Ua^2/(b^2-a^2)$, then the vector velocity is
$$
vec{v} = v_0left(1+frac{b^2}{r^2}right)sinthetahat{r}+v_0left(1-frac{b^2}{r^2}right)costhetahat{theta}
$$
answered Oct 6, 2013 at 19:52
Kyle KanosKyle Kanos
26.6k41 gold badges63 silver badges123 bronze badges
$endgroup$
8
Область,
занятую движущейся жидкостью, можно
себе представить как векторное
поле скоростей (см. рис. 2-7, а).
Рассмотрим
частный случай движения
жидкости, когда это векторное поле
является потенциальным,
т.
е. таким, которое может быть описано
некоторой функцией

у,
z),
обладающей
следующим свойством (см. конец § 2-4):
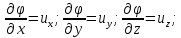
Дифференцируя
первое из этих уравнений по у
и
второе по х,
получаем:

вычитая
теперь из второго равенства (3-22) первое
равенство (3-22), имеем:

Рассуждая
аналогично, можем показать, что имеют
место также равенства:

Подставляя
выражения (3-23) и (3-24) в уравнения (3-20),
получаем
Ωx
= Ωy
= Ωz
= 0, (3-25)
Отсюда
можно сделать следующий вывод: если
рассматриваемое поле скоростей
имеет потенциальную функцию (потенциал
скорости

т.
е. является потенциальным, то средние
угловые скорости
О. вращения частиц жидкости относительно
своих мгновенных осей
должны равняться нулю, и мы будем иметь
безвихревое движение.
Следует
запомнить, что потенциальное
движение
всегда
является
безвихревым.
Можно
показать, что и наоборот: безвихревое
движение
жидкости
всегда
является
потенциальным.
Все
существующие формы движения жидкости
можно разбить на д в а вида:
а) движения
безвихревые (потенциальные), обладающие
потенциалом
скорости

б) движения
вихревые, для которых функция

поясненная
выше, не
существует.
В
случае потенциального
(безвихревого) потока жидкости приходится
отыскивать одну
функцию

удовлетворяющую соответствующимграничным
и начальным условиям и выражающую
согласно (3-21) компоненты скорости
их,
иу,
иz.
В
случае же вихревого движения задача
должна состоять, вообще говоря, в
отыскании трех функций, которые должны
зависеть от координат и времени,
удовлетворять соответствующим граничным
и начальным условиям и выражать
соответственно компоненты скорости
их,
иу,
иz.
Отсюда
видно, что исследование безвихревого
(потенциального) потока является
задачей значительно более простой, чем
исследование вихревого потока.
В
случае простейших потенциальных потоков
функция

Например, предположим, что нам задано
движение, характеризуемое условием:
их
= и0
= const;
иy
=
0; иz=
0.
Для
такого движения траектории частиц
жидкости представляют собой прямые
линии, параллельные
оси х,
а
поверхности равного потенциала (
— плоскости, параллельные координатной
плоскости уОz.
В
данном случае величина
Действительно,
дифференцируя это соотношение по
координатам, получаем приведенные выше
величины их,
иу,
иz.
В
более сложных случаях потенциального
движения для отыскания

особыми методами (изучаемыми в курсах
математики). Иногда может быть использован
так
называемый метод
сложения
(«наложения»
— суперпозиции)
потенциальных
потоков.
Он
заключается в следующем.
Положим,
что нам известно несколько потенциальных
функций:
1,
2,
3,
. . .,
n.
каждая из которых дает вполне определенный
потенциальный
поток.
Возьмем
алгебраическую сумму указанных функций:

Можно
доказать, что функция

(доказательстваздесь
не приводим). Такой поток будет более
сложным. Например, составляющая их
скорости
этого
потока будет
где


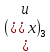
. . . .,
составляющие их
скорости
для указанных простейших потоков,
найденные в соответствующей точке.
Из
сказанного заключаем, что новый поток,
описываемый функцией

характеризуетсяследующим:
скорость в любой точке такого потока
равна геометрической
сумме
соответствующих
скоростей простейших потоков:
где
.
— векторы скорости простейших потоков,
найденные для рассматриваемой точки
заданной области.
Если
мы имеем сложный поток, то, как ясно из
сказанного, для отыскания ф можно иногда
поступить
следующим образом. Разложить скорости
и
сложного
потока на составляющие их (и1,
и2,
и3,
.
. ,). Рассматривая затем отдельно поле
скоростей и1,
и2,
и3,
.
. , можем найти для каждого простейшего
поля свою потенциальную функцию (
1,
2,
3,
.
. ,) Наконец, по формуле (3-25′) вычислить
искомую функцию

Соседние файлы в папке Чугаев_1
- #
- #
- #
- #
- #
- #
Как найти скорость тела, если дана его масса и потенциальная энергия?
-
Потенциальную энергию нужно прировнять к Кинетической энергии и получим,
mgh=mv^2/2,
отсюда, зная потенциальную энергию и массу тела, выведем скорость.
- Комментировать
- Жалоба
- Ссылка
Знаешь ответ на этот вопрос?
Сомневаешься в правильности ответа?
Получи верный ответ на вопрос 🏆 «Как найти скорость тела, если дана его масса и потенциальная энергия? …» по предмету 📕 Физика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Физика » Как найти скорость тела, если дана его масса и потенциальная энергия?
Потенциал скорости (видео обзоры)
Потенциал скорости это
(от латинского potentia — сила) — скалярная функция (φ) пространственных координат и времени, градиент которой равен вектору скорости V среды:
V = grad(φ).
П. с. существует для безвихревых течений, и введение П. с. позволяет эффективно их исследовать.
Уравнение для определения П. с. получается в результате подстановки приведённого выражения в неразрывности уравнение.
Для несжимаемой жидкости П. с. удовлетворяет уравнению Лапласа ((∆φ) = 0) и является гармонической функцией. В этом случае П. с. допускает простую физическую интерпретацию: П. с. данного распределения скорости безвихревого течения есть увеличенный в -1/Q (Q — плотность среды) раз импульс сил давления, требуемый для приведения среды (первоначально находившейся в состоянии покоя) в данное движение.
Для заданного поля скоростей П. с. в произвольной точке В можно найти интегрированием вдоль некоторой кривой, начинающейся в точке А с известным значением потенциала:
(φ)в = (φ)a + ∫ваVdr,
где dr — направленный элемент кривой. При движении в односвязной области П. с. является однозначной функцией r, а значение интеграла не зависит от пути интегрирования. Для многосвязной области П. с. в общем случае неоднозначен, и его значение в точке В зависит от формы кривой, вдоль которой проводится интегрирование.
Источник: Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев. 1994.
Видео
Скорость движения электронов
Уже упоминалось, что электроны движутся в направлении анода ускоренно, и это без всяких преувеличений соответствует действительности. В тот момент, когда электрон покидает область катода, его скорость теоретически принимается равной нулю, однако, он, находясь в постоянном электрическом поле анода, начинает двигаться ускоренно, и приобретает энергию, пропорциональную ускоряющему напряжению:
е — заряд электрона, принимается равным ≈ 1,602 х 10 -19 Кл;
те — масса электрона, принимается равной ≈ 9,11 х 10 -31 кг;
Решая это уравнение относительно скорости электрона υ, получим следующее выражение:
В науке часто используется отношение заряда электрона к его массе, е/те, которое имеет приближенное значение 1,7588 х 10 11 Кл/кг. При приложении к аноду относительно катода напряжения 100 В электрон достигнет поверхности анода, имея скорость порядка 6 х 10 б м/с.
Если использовать предыдущее выражение и подставить в него ускоряющее напряжение 512 кВ, (величина, соответствующая, например, напряжению в дальних линиях электропередач), то получится, что скорость электрона может превысить скорость света, что, естественно, является невозможным. Причина заключается в том, что приведенное упрощенное выражение справедливо только для массы покоя электрона, однако, при движении с околосветовыми скоростями масса электрона возрастает, требуя бесконечно большого значения напряжения для ускорения электрона до околосветовых скоростей. С учетом этих условий необходимо использовать более сложное уравнение, предложенное Элли (Alley) и Этвудом (Atwood):
в котором с — скорость света в вакууме, примерно равна 2,998 х 10 8 м/с.
В качестве домашнего примера действие принципа относительности можно продемонстрировать на цветном телевизоре. Для исправного цветного кинескопа напряжение на втором аноде составляет порядка 25 кВ, поэтому скорость электрона в момент удара о поверхность кинескопа составляет более 300 млн км/час, однако более простое уравнение предсказывает скорость, на 3,5% более высокую.
В рентгеновских медицинских установках мишень бомбардируется электронами, имеющими очень высокую скорость, так как для возникновения рентгеновского излучения скорость электрона при соударении должна значительно превышать 300 млн км в час. Поэтому в кинескопах домашних телевизоров и мониторов (для снижения интенсивности рентгеновского излучения) не используется ускоряющее напряжение, превышающее 25 кВ, хотя при этом можно было бы обеспечить более высокую четкость и фокусировку изображения.
Необходимо учесть, что расстояние между анодом и катодом не входит в каждое из уравнений, хотя теоретически бесконечное расстояние позволило бы бесконечно возрасти времени, во время которого происходит ускорение движения, и даже при сравнительно небольших ускорениях скорость при ударе могла бы оказаться значительной.
Очень многие явления, происходящие внутри электронных ламп, могут быть поняты при понимании процессов, происходящих при ускоренном движении электрона в электрическом поле анода, приобретении им кинетической энергии и процессах передачи энергии электрона при ударе, когда он достигает анода.
Все сказанное выше вполне справедливо для обсуждения скорости движения ускоренных положительным полем электронов, подлетающих к аноду. Однако в области катода картина совсем иная. Дело в том, что кинетическая энергия электронов, преодолевших работу выхода из металла и покинувших катод, оказывается различной. Таким образом, отрываясь от катода, электроны начинают движение к аноду с различными начальными скоростями. Они невелики, но при детальном рассмотрении их нельзя считать одинаковыми, как это предполагалось выше, когда рассматривался ускоренный поток электронов, подлетающих к аноду. Как будет показано ниже, управление электронным потоком в триодах и более сложных электронных лампах осуществляется как раз вблизи катода. Из физической статистики известно, что из-за различных кинетических энергий, скорости электронов, вылетающих из катода распределены по так называемому закону распределения Максвелла. Однако, для дальнейших рассуждений наиболее важным фактом является тот факт, что электроны, вылетающие из катода, обладают различными кинетическими энергиями.
Источник
Электрон в электрическом поле
Движение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле.
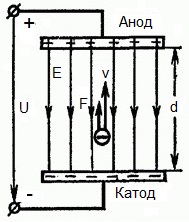
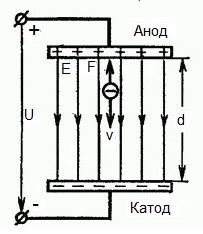
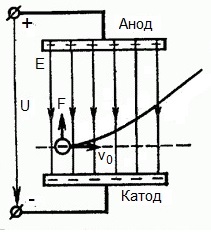
На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами.
К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля:
Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться.
Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так:
В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой:
Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна:
Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна:
Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом:
То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U.
В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина:
Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь:
Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути.
Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна:
Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно:
Теперь рассмотрим пример когда электрон движется в тормозящем однородном электрическом поле. То есть поле направлено как и прежде, но электрон начинает двигаться наоборот — от анода к катоду.
Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду.
Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле».
От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону.
Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение.
Если же начальная кинетическая энергия электрона меньше данной критической величины, то электрон не достигнет катода. В определенный момент он остановится, затем начнет равноускоренное движение обратно — к аноду. В итоге поле вернет ему энергию, которая израсходовалась в процессе торможения.
А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E.
Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду.
Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Движение электронов в ускоряющем поле
Движение электронов в однородном электрическом поле
Движение электронов в электромагнитном поле.
Основным процессом во всех электронных приборах является взаимодействие движущихся электронов с электрическим полем. Электрон представляет собой частицу материи с отрицательным зарядом, значение которого равно e=1,6•10 -19 Кл (Кулон). Масса неподвижного электрона m=9,1•10 -28 г. С возрастанием скорости масса электрона увеличивается. Теоретически, при скорости электрона равной скорости света с=3•10 8 м/с, его масса должна стать бесконечно большой. В обычных электронных приборах скорость электрона не превышает 0,1 от скорости света, в связи с чем, массу электрона в РЭА принимают постоянной и равной массе неподвижного электрона.
Электрическое поле в электронных приборах может быть однородным и неоднородным. Наиболее простыми для изучения являются закономерности движения электронов в однородном электрическом поле. В зависимости от угла между вектором скорости электрона и вектором напряженности электрического поля, электрическое поле может ускорять, тормозить движение электрона, или делать его траекторию криволинейной.
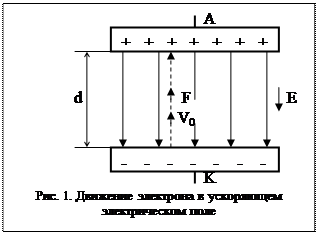
На рис. 1 изображено в виде силовых линий (линий напряженности) однородное электрическое поле между двумя электродами, например между катодом и анодом диода. Если разность потенциалов между электродами U, а расстояние – d, то напряженность поля E=U/d/ Для однородного поля Е – постоянная величина.
Пусть из электрода, имеющего более низкий потенциал (из К) вылетает электрод с кинетической энергией W0 и начальной скоростью V0, направленной вдоль силовых линий поля. Поле ускоряет движение электрона. Напряженность поля численно равна силе, действующей на единичный положительный заряд. Поэтому сила действия на электрон равна F=-e•E. Знак минус поставлен потому, что сила F направлена в сторону противоположную вектору Е. Под действием силы F электрон получает ускорение a=F/m. Двигаясь прямолинейно, электрон приобретает максимальную скорость V и кинетическую энергию W в конце своего пути, т.е. при ударе об электрод А. Таким образом, в ускоряющем электрическом поле кинетическая энергия электрона возрастает за счет работы электрического поля по перемещению электрона. В соответствии с законом сохранения энергии увеличение кинетической энергии электрона W-W0 , равно работе поля, которая определяется произведением перемещаемого заряда е на пройденную им разность потенциалов U:
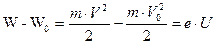
Если начальная скорость электрона равна нулю, то
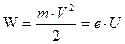
Эта же формула применяется, если V0 неизвестна, но известно, что она много меньше конечной скорости V (V0 -3 мкс=1нс.
Время пролета электрона определяет одну из важнейших характеристик электронных приборов – их быстродействие. В следствие неоднородности электрического поля в электронных приборах расчет времени пролета в них электронов более сложен.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник