Enter the total dynamic pressure and the fluid mass density into the calculator to determine the velocity. This calculator can also evaluate the pressure or density given the other variables are known.
- All Velocity Calculators
- Pressure to Head Calculator
- Velocity Calculator
- Flow Rate Pressure Calculator
- Water Pressure Calculator
- Pitot Tube Calculator
Pressure to Velocity Formula
The following formula is used to calculate a velocity from dynamic pressure.
- Where V is the velocity (m/s)
- q is the dynamic pressure (pascals)
- p is the fluid mass density (kg/m^3)
To calculate velocity from pressure, multiply the dynamic pressure by 2, divide by the fluid mass density, then take the square root of that result.
Pressure to Velocity Definition
Calculating a velocity from a dynamic pressure requires that you also know the density. Dynamic pressure arises from the movement of fluid through a volume.
Pressure to Velocity Example
How to calculate velocity from pressure?
The first step in calculating a velocity from pressure is to determine or measure the dynamic pressure that happens as a result of the fluid flow through the pipe.
In this example, the dynamic pressure is found to be 200 pascals.
The next step is to determine the density of the fluid. In this case, the density is measured to be 1.225 kg/m^3.
Finally, calculate the velocity from the dynamic pressure and density using the formula above:
V = Sqrt [ (2*q/p) ]
V = Sqrt [ (2*200/1.225) ]
V = 18.07 m/s.
FAQ
What is dynamic pressure?
Dynamic pressures are pressure differentials that arise from the flow of a fluid through a constrained area.
What is the relationship between pressure and velocity in fluid dynamics?
Bernoulli’s equation describes the relationship between pressure and velocity in fluid dynamics.
It states that in a fluid flowing through a pipe or channel, an increase in the velocity of the fluid will result in a decrease in pressure, and vice versa.
How does pressure change with velocity in a fluid?
In a fluid, pressure and velocity are inversely proportional to each other.
As the velocity of the fluid increases, the pressure decreases, and as the velocity decreases, the pressure increases.
What is Bernoulli’s equation used for?
Bernoulli’s equation describes the relationship between pressure, velocity, and height in a fluid flow system.
It is commonly used in various fields such as aerodynamics, hydrodynamics, and mechanics to analyze the flow of fluids.
Why does the pressure decrease with velocity in a fluid flow?
The pressure decreases with velocity in a fluid flow due to energy conservation.
As the fluid flows and its velocity increases, its pressure decreases to conserve the total energy of the fluid.
What is the difference between dynamic pressure and static pressure?
Dynamic pressure is the pressure that arises due to the motion of a fluid, while static pressure is the pressure exerted by a fluid at rest.
Dynamic pressure is proportional to the square of the velocity of the fluid, while the fluid’s density and height determine static pressure.
How is pressure affected by the velocity of a fluid?
The velocity of a fluid affects pressure by changing the dynamic pressure of the fluid.
An increase in velocity results in an increase in the dynamic pressure, and a decrease in the static pressure.
What is the effect of temperature on the pressure in a fluid?
The temperature affects pressure in a fluid due to its impact on the fluid’s density.
An increase in temperature will increase the fluid’s volume, causing the pressure to decrease.
A decrease in temperature will result in a decrease in the fluid’s volume, causing the pressure to increase.
How does fluid velocity affect the pressure drop in a pipe?
The velocity of a fluid affects the pressure drop in a pipe by changing the dynamic pressure of the fluid. An increase in fluid velocity will result in an increase in the dynamic pressure, causing a more significant pressure drop.
A decrease in fluid velocity will result in a decrease in the dynamic pressure, causing a smaller pressure drop.
How does the viscosity of a fluid affect the relationship between pressure and velocity?
Viscosity affects the relationship between pressure and velocity in a fluid by slowing down the flow of the fluid.
A higher-viscosity fluid will have a lower velocity, resulting in higher pressure, while a lower viscosity fluid will have a higher velocity, resulting in lower pressure.
Связь давления и скорости в потоке
Связь давления и
скорости в потоке жидкости —
обратная: если в каком-то месте потока
скорость увеличивается, то давление
здесь малó,
и, наоборот, там, где скорости невелики,
давление повышенное. Эту закономерность
объясним на основе уравнения Бернýлли.
Рассмотрим работу
водоструйного насоса (см. рис. 11). На
подходе по нагнетательному трубопроводу
1 поток рабочей жидкости имеет
относительно небольшую скорость
v1
и высокое избыточное давление pизб1.
Проходя через соплó
2, поток сужается, скорость его резко
возрастает до v2.
Для дальнейших рассуждений запишем
уравнение Бернýлли
так:

Здесь нет z1
и z2,
так как труба горизонтальная, а величиной
потерь напора DH»
0
пренебрегаем. Так как в правой части
уравнения кинетическая составляющая
энергии потока резко возросла из-за
увеличения v2,
то потенциальная составляющая, связанная
с избыточным давлением после соплá
pизб2,
наоборот, уменьшится. Величину pизб2
можно выразить из этого уравнения и
найти численное значение. Если pизб2
получается отрицательным, то, значит,
возник вакуум (полное давление в струе
стало меньше атмосферного). В последнем
случае пьезометрическая линия опустится
ниже отметки самой струи (см. рис 11).
Таким образом в струе
рабочей жидкости после соплá
образуется область пониженного
давления или даже вакуум, что вызывает
подсос транспортируемой жидкости
по всасывающему трубопроводу 3 (см. рис.
11). Далее обе жидкости смешиваются в
горловине 4 и транспортируются по
отводящему трубопроводу 5.
Водоструйные насосы
не имеют трущихся частей, в этом их
преимущество перед механическими.
По их принципу работают также эжекторы,
гидроэлеваторы, насосы для создания
вакуума.
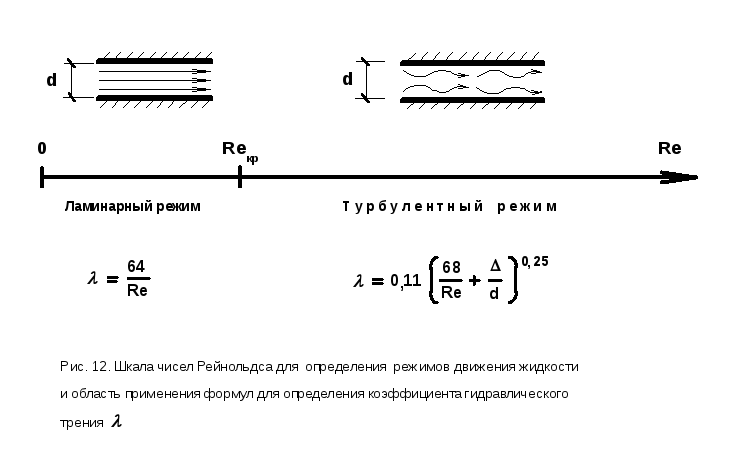
Режимы движения жидкости
При проведении
гидравлического расчёта в первую очередь
нужно выяснять: какой режим движения
будет наблюдаться у данного потока?
Режимы движения всех
потоков (напорных и безнапорных) делятся
на два типа (рис. 12):
1) ламинарный, то есть
спокойный, параллельноструйный, при
малых скоростях;
2) турбулентный, то
есть бурлящий, вихреобразный, с
водоворотами, при больших скоростях.
Для выяснения типа
режима нужно рассчитать число Рейнольдса
Re
и сравнить его с критическим Reкр.
Число Рéйнольдса
Re
—
это безразмерный критерий, вычисляемый
по формулам:
— для напорных
потоков
Re
=vd/n
,
где d
—
внутренний диаметр напорного трубопровода;
— для безнапорных
потоков
Re
=vR/n,
где R
—
гидравлический радиус безнапорного
потока, м
(см. с. 14).
Критическое число
Рейнольдса Reкр
—
это число Рейнольдса, при котором
наступает смена режима движения.
Для напорных потоков
Reкр=2320,
для безнапорных
потоков
Reкр
»
500.
Упрощённо режим
движения потока можно определить по
шкале чисел Рейнольдса (см. рис. 12).
Рассмотрим пример с напорной водопроводной
трубой, у которой d=20
мм, v=1
м/с, n
=10—6
м2/с.
Для потока в данной трубе число
Рейнольдса составит:
Re=1×0,02/10—6
=
20000.
Число 20000
больше, чем
Reкр=2320
(для напорных
потоков) и на рис.12 оно находится в правой
части шкалы, следовательно, режим потока
турбулентный и все дальнейшие
гидравлические расчёты должны проводиться
только по зависимостям и формулам для
этого режима.
Зависимость давления жидкости от скорости ее течения
В предыдущих параграфах были рассмотрены законы равновесия жидкостей и газов. Теперь рассмотрим некоторые явления, связанные с их движением.
Движение жидкости называют течением, а совокупность частиц движущейся жидкости потоком. При описании движения жидкости определяют скорости, с которыми частицы жидкости проходят через данную точку пространства. Если в каждой точке пространства, заполненного движущейся жидкостью, скорость не изменяется со временем, то такое движение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит через данную точку пространства с одним и тем же значением скорости. Мы будем рассматривать только стационарное течение идеальной несжимаемой жидкости. Идеальной называют жидкость, в которой отсутствуют силы трения.
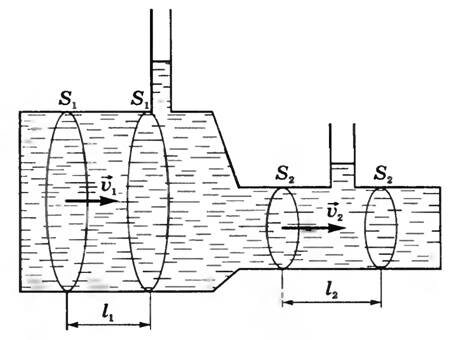
Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля, передает внешнее давление ко всем точкам жидкости без изменения. Но когда жидкость течет без трения по трубе переменного поперечного сечения, давление в разных местах трубы неодинаково. Оценить распределение давлений в трубе, по которой течет жидкость, можно с помощью установки, схематически изображенной на рисунке 1. Вдоль трубы впаивают вертикальные открытые трубки-манометры. Если жидкость в трубе находится под давлением, то в манометрической трубке жидкость поднимается на некоторую высоту, зависящую от давления в данном месте трубы. Опыт показывает, что в узких местах трубы высота столбика жидкости меньше, чем в широких. Это значит, что в этих узких местах давление меньше. Чем это объясняется?
Рис. 1
Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рис. 1). Выделим мысленно несколько сечений в трубе, площади которых обозначим S1 и S2. При стационар ном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
Пусть υ1 — скорость жидкости через сечение S1, υ2 — скорость жидкости через сечение S2. За время Δt объемы жидкостей, протекающих через эти сечения, будут равны:
(~begin{matrix} Delta V_1 = l_1S_1 = upsilon_1 Delta t_1 cdot S_1 ; \ Delta V_2 = l_2S_2 = upsilon_2 Delta t_2 cdot S_2 . end{matrix})
Так как жидкость несжимаема, то ΔV1 = ΔV2. Следовательно, υ1S1 = υ2S2 или υS = const для несжимаемой жидкости. Это соотношение называется уравнением неразрывности.
Из этого уравнения (~frac{upsilon_1}{upsilon_2} = frac{S_2}{S_1}) , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются. Следовательно, на жидкость, поступающую в более узкую часть трубы, действует со стороны жидкости, еще находящейся в широкой части трубы, некоторая сила. Такая сила может возникнуть только за счет разности давлений в различных частях жидкости. Так как сила направлена в сторону узкой части трубы, то в широком участке трубы давление должно быть больше, чем в узком. Учитывая уравнение неразрывности, можно сделать вывод: при стационарном течении жидкости давление меньше в тех местах, где больше скорость течения, и, наоборот, больше в тех местах, где скорость течения меньше.
К этому выводу впервые пришел Д. Бернулли, поэтому данный закон называют законом Бернулли.
Применение закона сохранения энергии к потоку движущейся жидкости позволяет получить уравнение, выражающее закон Бернулли (приводим без вывода)[~p_1 + frac{rho upsilon^2_1}{2} = p_2 + frac{rho upsilon^2_2}{2}] — уравнение Бернулли для горизонтальной трубки.
Здесь p1 и p2 — статические давления, ρ — плотность жидкости. Статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю. Такое давление измерил бы манометр, движущийся вместе с потоком. Неподвижная монометрическая трубка с отверстием, обращенным навстречу потоку, измерит давление (~p = p_1 + frac{rho upsilon^2_1}{2}).
Слагаемые (~frac{rho upsilon^2_1}{2}) и (~frac{rho upsilon^2_2}{2}) имеют, с одной стороны, размерность давления, с другой — размерность объемной плотности энергии, т. е. энергии, приходящейся на единицу объема. Действительно, (~W_k = frac{m upsilon^2}{2}), масса жидкости m = ρV. Если V = 1 м3, то (~W_k = frac{rho upsilon^2}{2}). Поэтому (~frac{rho upsilon^2}{2}) — называют динамическим давлением. Это кинетическая энергия потока в единичном объеме жидкости (объемная плотность энергии).
Если трубка не горизонтальная, то надо учитывать и гидростатическое давление жидкости. Уравнение Бернулли будет иметь вид:
(~p_1 + rho gh_1 + frac{rho upsilon^2_1}{2} = p_2 + rho gh_2 + frac{rho upsilon^2_2}{2},)
где h1 и h2 — высоты, на которых находятся сечения S1 и S2.
Закон Бернулли лежит в основе принципа действия многих технических устройств и приборов: водоструйного насоса, пульверизатора, форсунки карбюратора. Закон Бернулли позволяет объяснить возникновение подъемной силы крыла самолета.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 106-108.
Изменение в правилах «Опознайки»
Один объект для опознания — одна тема.
Запрещается размещать групповые фотографии или несколько разных объектов для опознания.
Для публикации сообщений создайте учётную запись или авторизуйтесь
Вы должны быть пользователем, чтобы оставить комментарий
Войти
Уже есть аккаунт? Войти в систему.
Войти
Содержание
- 1 Скорость потока жидкости в трубе формула
- 2 Скорость потока жидкости в трубе формула
- 3 Расход воды через трубу при нужном давлении
- 3.1 Табличные стандартные данные и средние показатели по основным параметрам
- 3.2 Способы вычисления зависимостей водорасхода и диаметра трубопровода
- 4 Расчет расхода воды по диаметру трубы и давлению по таблице и СНИПу 2.04.01-85
- 4.1 Калькулятор для расчета воды онлайн
- 4.2 Какие факторы влияют на проходимость жидкости через трубопровод
- 4.3 Вычисления сечения по СНИП 2.04.01-85
- 5 Расчет скорости течения жидкости в трубопроводе
Скорость потока жидкости в трубе формула
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.
Для того чтобы вычислить диаметр необходимо знать:
Вот необходимые формулы, которые нужно знать:
Сопротивление движению теплоносителя.
Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.
Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.
Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.
Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.
В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.
Решение: Необходимо воспользоваться вышеуказанными формулами:
S=3.14•0,012 2 /4=0,000113 м 2
Q=0,000113•1=0,000113 м 3 /с = 0,4 м 3 /ч.
Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.
Q=40л/мин=0,000666666 м 3 /с
Из выше указанных формул получил такую формулу.
Каждый насос имеет вот такую расходно-сопротивляемую характеристику:
Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.
Более детально потеря напора по длине трубопровода рассматривается в этой статье:
А теперь рассмотрим задачу из реального примера.
Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.
Найти максимальный расход = ?
Для решения необходимо знать график насосов: Зависимость расхода от напора.
В нашем случае будет такой график:
Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.
По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).
Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
Поэтому решаем задачу ступенчато.
Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.
Находим скорость движения воды
Q=45 м 3 /ч = 0,0125 м 3 /сек.
V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
Находим число рейнольдса
ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.
Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.
Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
У меня попадает на вторую область при условии
10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216
Далее завершаем формулой:
h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:
Теперь делаем оригинальный расчет при расходе равный 64м 3 /час
Q=64 м 3 /ч = 0,018 м 3 /сек.
V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021
h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
Отмечаем на графике:
Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).
Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.
Для проверки проверим:
Q=54 м 3 /ч = 0,015 м 3 /сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
Итог: Мы попали на Нпот=14,89=15м.
А теперь посчитаем сопротивление на поворотах:
Формула по нахождению напора на местном гидравлическом сопротивление:
ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.
Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.
Скорость 1,91 м/с
h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.
Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
Давайте теперь решим целиком задачку с отводами.
При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.
При этой скорости (2,29 м/с) находим сопротивление на поворотах:
h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.
Складываем потери напора: 10,46+5,67=16,13м.
Отмечаем на графике:
Решаем тоже самое только для расхода в 55 м 3 /ч
Q=55 м 3 /ч = 0,015 м 3 /сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.
Складываем потери: 14,89+3,78=18,67 м
Рисуем на графике:
Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.
В итоге, на размер диаметра влияют:
Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.
Данная статья является частью системы: Конструктор водяного отопления
Скорость потока жидкости в трубе формула
Скорость потока жидкости в трубе формула Диаметр трубопроводов, скорость течения и расход теплоносителя. Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И
Источник: infobos.ru
Скорость потока жидкости в трубе формула
При движении жидкости в круглой трубе скорость равна нулю у стенок трубы и максимальна на оси трубы. Полагая течение ламинарным, найдем закон изменения скорости с расстоянием от оси трубы.
Выделим воображаемый цилиндрический объем жидкости радиуса и длины l (рис. 77.1). При стационарном течении в трубе постоянного сечения скорости всех частиц жидкости остаются неизменными. Следовательно, сумма внешних сил, приложенных к любому объему жидкости, равна нулю. На основания рассматриваемого цилиндрического объема действуют силы давления, сумма которых равна Эта сала действует в направлении движения жидкости. Кроме того, на боковую поверхность цилиндра действует сила трения, равная (Имеется в виду значение на расстоянии от оси трубы). Условие стационарности имеет вид
Скорость убывает с расстоянием от оси трубы. Следовательно, отрицательна и Учтя это, преобразуем соотношение (77.1) следующим образом:
Разделив переменные, получим уравнение:
Интегрирование дает, что
Постоянную интегрирования нужно выбрать так, чтобы скорость обращалась в нуль на стенках трубы, т. е. — радиус трубы).
Из этого условия
Подстановка значения С в (77.2) приводит к формуле
Значение скорости на оси трубы равно
С учетом этого формуле (77.3) можно придать вид
Таким образом, при ламинарном течении скорость изменяется с расстоянием от оси трубы по параболическому закону (рис. 77.2).
При турбулентном течении скорость в каждой точке меняется беспорядочным образом. При неизменных внешних условиях постоянной оказывается средняя (по времени) скорость в каждой точке сечения трубы. Профиль средних скоростей при турбулентном течении изображен на рис. 77.3. Вблизи стенок трубы скорость изменяется гораздо сильнее, чем при ламинарном течении, в остальной же части сечения скорость изменяется меньше.
Полагая течение ламинарным, вычислим поток жидкости Q, т. е. объем жидкости, протекающий через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца ширины (рис. 77.4). Через кольцо радиуса пройдет за секунду объем жидкости, равный произведению площади кольца на скорость течения в точках, находящихся на расстоянии от оси трубы.
Приняв во внимание формулу (77.5), получим:
Чтобы получить поток Q, нужно проинтегрировать выражение (77.6) по в пределах от нуля до R: я 9
— площадь сечения трубы). Из формулы (77.7) следует, что при ламинарном течении среднее (по сечению) значение скорости равно половине значения скорости на. оси трубы.
Подставив в (77.7) значение (77.4) для
получим для потока формулу
Эта формула называется формулой Пуазейля. Согласно (77.8) поток жидкости пропорционален перепаду давления на единице длины трубы, пропорционален четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости жидкости. Напомним, что формула Пуазейля применима только при ламинарном течении.
Соотношение (77.8) используется для определения вязкости жидкостей. Пропуская жидкость через капилляр известного радиуса и измеряя перепад давления и поток Q, можно найти
Скорость потока жидкости в трубе формула
Научная библиотека популярных научных изданий
Источник: scask.ru
Расход воды через трубу при нужном давлении
Содержание статьи
Основная задача расчёта объёма потребления воды в трубе по её сечению (диаметру) – это подобрать трубы так, чтобы водорасход не был слишком большой, а напор оставался хороший. При этом необходимо учесть:
- диаметры (ДУ внутреннего сечения),
- потери напора на рассчитываемом участке,
- скорость гидропотока,
- максимальное давление,
- влияние поворотов и затворов в системе,
- материал (характеристики стенок трубопровода) и длину и т.д..
Подбор диаметра трубы по расходу воды с помощью таблицы считается более простым, но менее точным способом, чем измерение и расчёт по давлению, скорости воды и прочим параметрам в трубопроводе, сделанный по месту.
Табличные стандартные данные и средние показатели по основным параметрам
Для определения расчётного максимального расхода воды через трубу приводится таблица для 9 самых распространённых диаметров при различных показателях давления.
Среднее значение давления в большинстве стояках находится в интервале 1,5-2,5 атмосфер. Существующая зависимость от количества этажей (особенно заметная в высотных домах) регулируется путём разделения системы водообеспечения на несколько сегментов. Водонагнетение с помощью насосов влияет и на изменение скорости гидропотока. Кроме того, при обращении к таблицам в расчёте водопотребления учитывают не только число кранов, но и количество водонагревателей, ванн и др. источников.
Способы вычисления зависимостей водорасхода и диаметра трубопровода
С помощью нижеприведённых формул можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода воды.
В данной формуле водорасхода:
- под q принимается расход в л/с,
- V – определяет скорость гидропотока в м/с,
- d – внутреннее сечение (диаметр в см).
Зная водорасход и d сечения, можно, применив обратные вычисления, установить скорость, или, зная расход и скорость – определить диаметр. В случае наличия дополнительного нагнетателя (например, в высотных зданиях), создаваемое им давление и скорость гидропотока указываются в паспорте прибора. Без дополнительного нагнетания скорость потока чаще всего варьируется в интервале 0,8-1,5 м/сек.
Для более точных вычислений принимают во внимание потери напора, используя формулу Дарси:
Для вычисления необходимо дополнительно установить:
- длину трубопровода (L),
- коэффициент потерь, который зависит от шероховатостей стенок трубопровода, турбулентности, кривизны и участков с запорной арматурой (λ),
- вязкость жидкости (ρ).
Зависимость между значением D трубопровода, скоростью гидропотока (V) и водорасходом (q) с учётом угла уклона (i) можно выразить в таблице, где две известные величины соединяются прямой линией, а значение искомой величины будет видно на пересечении шкалы и прямой.
Для технического обоснования также строят графики зависимости эксплуатационных и капитальных затрат с определением оптимального значения D, которое устанавливается в точке пересечения кривых эксплуатационных и капитальных затрат.
- способа расчёта сопротивления,
- материала и вида трубопроводных систем (сталь, чугун, асбоценмент, железобетон, пластмасса), где принимается во внимание, что, например, пластиковые поверхности менее шероховатые, чем стальные, и не подвергаются коррозии,
- внутреннего диаметры,
- длины участка,
- падения напора на каждый метр трубопровода.
В некоторых калькуляторах учитываются дополнительные характеристики трубопроводных систем, например:
- новые или не новые с битумным покрытием или без внутреннего защитного покрытия,
- с внешним пластиковым или полимерцементным покрытием,
- с внешним цементно-песчаным покрытием, нанесённым разными методами и др.
Расход воды через трубу при нужном давлении
Определение зависимости расхода объёма воды, диаметра трубы, давления и скорости потока 3 способами: с помощью таблицы, формул или расчётов онлайн-калькулятором.
Источник: hitropop.com
Расчет расхода воды по диаметру трубы и давлению по таблице и СНИПу 2.04.01-85
Предприятия и жилые дома потребляют большое количество воды. Эти цифровые показатели становятся не только свидетельством конкретной величины, указывающей расход.
Помимо этого они помогают определить диаметр трубного сортамента. Многие считают, что расчет расхода воды по диаметру трубы и давлению невозможен, так, как эти понятия совершенно не связаны между собой.
Но, практика показала, что это не так. Пропускные возможности сети водоснабжения зависимы от многих показателей, и первыми в этом перечне будут диаметр трубного сортамента и давление в магистрали.
Выполнять все расчеты рекомендуют еще на стадии проектирования строительства трубопровода, потому, что полученные данные определяют ключевые параметры не только домашнего, но и промышленного трубопровод. Обо всем этом и пойдет далее речь.
Калькулятор для расчета воды онлайн
Какие факторы влияют на проходимость жидкости через трубопровод
Критерии, оказывающие влияние на описываемый показатель, составляют большой список. Вот некоторые из них.
- Внутренний диаметр, который имеет трубопровод.
- Скорость передвижения потока, которая зависит от давления в магистрали.
- Материал, взятый для производства трубного сортамента.
Определение расхода воды на выходе магистрали выполняется по диаметру трубы, ведь эта характеристика совместно с другими влияет на пропускную способность системы. Так же расчитывая количество расходуемой жидкости, нельзя сбрасывать со счетов толщину стенок, определение которой проводится, исходя из предполагаемого внутреннего напора.
Можно даже заявить, что на определение «трубной геометрии» не влияет только протяженность сети. А сечение, напор и другие факторы играют очень важную роль.
Помимо этого, некоторые параметры системы оказывают на показатель расхода не прямое, а косвенное влияние. Сюда относится вязкость и температура прокачиваемой среды.
Подведя небольшой итог, можно сказать, что определение пропускной способности позволяет точно установить оптимальный тип материала для строительства системы и сделать выбор технологии, применяемой для ее сборки. Иначе сеть не будет функционировать эффективно, и ей потребуются частые аварийные ремонты.
Расчет расхода воды по диаметру круглой трубы, зависит от его размера. Следовательно, что по большему сечению, за определенный промежуток времени будет выполнено движение большего количества жидкости. Но, выполняя расчет и учитывая диаметр, нельзя сбрасывать со счетов давление.
Если рассмотреть этот расчет на конкретном примере, то получается, что через метровое трубное изделие сквозь отверстие в 1 см пройдет меньше жидкости за определенный временной период, чем через магистраль, достигающей в высоту пару десятков метров. Это закономерно, ведь самый высокий уровень расхода воды на участке достигнет максимальных показателей при самом высоком давлении в сети и при самых высоких размера ее объема.
Вычисления сечения по СНИП 2.04.01-85
Прежде всего, необходимо понимать, что расчет диаметра водопропускной трубы является сложным инженерным процессом. Для этого потребуются специальные знания. Но, выполняя бытовую постройку водопропускной магистрали, часто гидравлический расчет по сечению проводят самостоятельно.
Данный вид конструкторского вычисления скорости потока для водопропускной конструкции можно провести двумя способами. Первый – табличные данные. Но, обращаясь к таблицам необходимо знать не только точное количество кранов, но и емкостей для набора воды (ванны, раковины) и прочего.
Только при наличии этих сведений о водопропускной системе, можно воспользоваться таблицами, которые предоставляет СНИП 2.04.01-85. По ним и определяют объем воды по обхвату трубы. Вот одна из таких таблиц:
Расчет расхода воды по диаметру трубы и давлению по таблице и СНИПу -85
Расчет расхода воды по диаметру трубы и давлению необходимо произвести перед тем как … но на определение расхода воды влияет так же температура и вязкость среды, а так же материал, из которого состоит магистраль
Источник: trubanet.ru
Расчет скорости течения жидкости в трубопроводе
Автоклав объёмом 25,0 л наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости , её модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры жидкости на величину Т. Объёмной деформацией автоклава пренебречь.
V0 = 25,0л = 25*10-3 м3
Из-за повышения температуры объем жидкости увеличится на величину.
V = 536*10-6*25*10-3*21=0,2814*10-3 м3
Коэффициент объемного сжатия сведем с модулем упругости.
Он представляет собой относительное изменение объема жидкости, приходящееся на единицу давления.
Величина повышения давления.
Вертикальная цилиндрическая цистерна с полусферической крышкой до самого верха заполнена жидкостью, плотность которой . Диаметр цистерны D, высота её цилиндрической части Н. Манометр М показывает манометрическое давление Рм. Определить силу, растягивающую болты А, и горизонтальную силу, разрывающую цистерну по сечению 1-1.
Силой тяжести крышки пренебречь. Векторы сил показать на схеме.
Вертикальная сила Fz, растягивающую болты.
где V – объем тела давления
Расстояние по вертикали до пьезометрической плоскости (пп).
Объем тела давления как разность объемов цилиндра и полусферы.
Сила растягивающая болты.
Fz =*g*=998*9,81*=5249 Н
Горизонтальная сила, действующая на вертикальную полуцилиндрическую часть.
где p1 = рм+gh = g*0,288 D
– давление в центре тяжести С1 вертикальной проекции верхней полуцилиндрической части,
– площадь этой проекции (полукруг).
F1 = g *0,288D* = 0,036 П* g = 0,036П*998*9,81*1,63=4535Н
Горизонтальная сила, действующая на цилиндрическую часть.
– давление в центре тяжести вертикальной проекции цилиндрической части.
А2 – площадь этой проекции.
F2 = g ( НD =998*9,81*(.
Полная горизонтальная сила равна.
FX = F1 + F2 = 4535+120304=124839 Н.
Ответ: Fz = 5249H, Fx = 124839H.
Центробежный насос, перекачивающий жидкость Ж при температуре 20С, развивает подачу Q. Определить допустимую высоту всасывания hв, если длина всасывающего трубопровода l, диаметр d, эквивалентная шероховатость э, коэффициент сопротивления обратного клапана к, а показание вакуумметра не превышало бы pв.
Построить пьезометрическую и напорную линии. Данные в соответствии с вариантом задания выбрать из табл. 4.
Q = 1,9 л/с=1,9*10-3 м3/с
– кинематическая вязкость Ж
= 808 кг/м3 – плотность Ж
Выбираем два живых сечения в потоке, где известно наибольшее число входящих в уравнение Бернулли гидравлических параметров. За первое сечение 1-1 берем свободную поверхность жидкости в резервуаре А, за второе сечение 2-2 принимаем место подключения вакуумметра.
3. Для выбранных сечений уравнение Бернулли будет иметь вид:
Намечаем горизонтальную плоскость сравнения проходящую через центр тяжести сечения 1-1.
Геометрическая высота: Z1 = 0, Z2 = hв.
Давление: р1 = Ратм, р2 = Ратм – рв.
h=hтр+hм (сумма потерь на трение и местные потери)
Скорость течения жидкости в трубопроводе
Определяем режим течения жидкости, исходя из значения числа Рейнольдса по формуле:
– режим течения турбулентности.
Коэффициента гидравлического трения по формуле Альтшуля.
Потери напора от трения по длине трубопровода
Местные гидравлические потери.
– сумма коэффициентов местных сопротивлений (вход в трубу, клапан, поворот). жидкость пьезометрический гидравлический трение
Допустимая высота всасывания
Ответ: hв = 7,40 м.
Рабочая жидкость масло Ж, температура которого 50С, из насоса подводится к гидроцилиндру Ц через дроссель ДР. Поршень цилиндра со штоком перемещается против нагрузки Fсо скоростью п. Вытесняемая поршнем жидкость со штоковой полости попадает в бак Б через сливную линию, длина которой равна lc, а диаметр равен dc.
Определить внешнюю силу F, преодолеваемую штоком при его движении. Давление на входе в дроссель определяется показанием манометра М, а противодавление в штоковой полости цилиндра потерями давления в сливной линии. Коэффициент расхода дросселя принять равным = 0,64, а диаметр отверстия дросселя dд. Диаметр поршня Dп, а диаметр штока Dш. К.п.д. гидроцилиндра: объёмный 0 = 1,0, механический м.
Расчет скорости течения жидкости в трубопроводе
Расчет скорости течения жидкости в трубопроводе Автоклав объёмом 25,0 л наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости , её модуль упругости Е.
Источник: studwood.ru