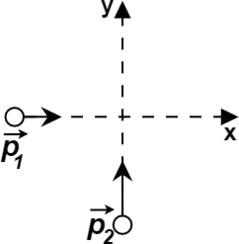
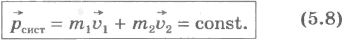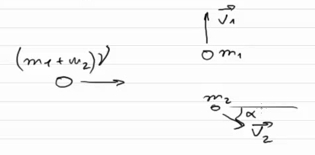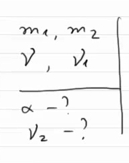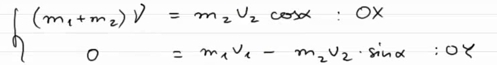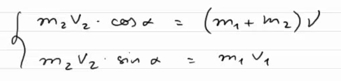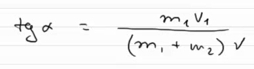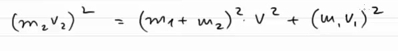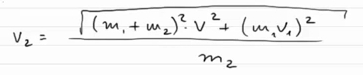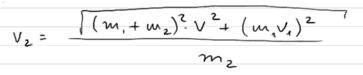Снаряд массой 2 кг, летящий со скоростью 200 м/с, разрывается на два осколка. Первый осколок массой 1 кг летит под углом 90° к первоначальному направлению со скоростью 300 м/с. Найдите скорость второго осколка.
Спрятать решение
Решение.
По закону сохранения импульса
где
(см. рис.).
Запишем это равенство в проекциях на горизонтальную и вертикальную оси:
Скорость второго осколка равна
Ответ: 500 м/с.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); III) представлен правильный ответ с указанием единиц измерения искомой величины |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но допущена ошибка в ответе или в математических преобразованиях или вычислениях. ИЛИ Представлены только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в 1 или 2 балла |
0 |
| Максимальный балл | 2 |
Снаряд, летевший в
горизонтальном направлении со скоростью 20 м/с , разорвался на два осколка
массами 10 кг и 5 кг. Скорость меньшего осколка равна 20 м/с и направлена
вертикально вверх. Определите модуль и направление скорость движения большего
осколка.
Решение.
Материальными объектами
задачи являются: снаряд, два осколка, поверхность Земли, гравитационное поле
Земли и воздух. Снаряд и осколки примем за материальные точки.
Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной. Начало координат выберем
на поверхности Земли. Ось OX
направим горизонтально в направлении движения снаряда, ось OY – вертикально вверх.
В физическую систему
включим
снаряд и осколки. Земля и воздух по отношению к выделенной физической
системе являются внешними телами. Даже если не учитывать взаимодействие
физической системы с воздухом, она будет незамкнутой. Это обусловлено действием
на тела системы ничем не скомпенсированной силы тяжести.
Можно выделить два
состояния системы: начало взрыва и конец взрыва. Если учесть, что промежуток
времени между началом и концом взрыва небольшой, а внутренние силы, возникающие
при этом, велики по сравнению с силой тяжести, то выделенную физическую систему
можно считать практически замкнутой и описать законом сохранения импульса.
Начальный импульс
физической системы равен p1 = (m1 + m2)v , а ее конченый импульс – p2 = m1v1 + m2v2 .
Согласно закону сохранения
импульса: p
= p2 или
.
Если спроецировать
векторные величины на оси координат, получим
.
Откуда
.
Расчеты дают: v1 = 32 м/с, α = 19° . Таким образом, скорость большого осколка
равна 32 м/с и направлена вниз под углом α = 19° к горизонту.
Ответ: v1 = 32 м/с, α = 19° .
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Закон сохранения импульса.
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Закон сохранения импульса
Закон сохранения импульса
Закон сохранения импульса относится к одному из фундаментальных понятий физики. Закон сохранения импульса гласит, что если сумма внешних сил равна нулю, то импульс системы тел сохраняется.
В формульном обозначении этот закон гласит, что импульс системы, который можно представить как произведение массы на скорость для первого тела плюс произведение массы на скорость второго тела и так далее, является постоянным. То есть математическая формулировка закона сохранения импульса выглядит так:
Важно помнить, что закон сохранения импульса выполняется, если вы работаете в замкнутой системе, а замкнутая система – это система, в которой сумма внешних действующих сил будет равняться нулю.
Если у вас выполняется два этих условия, то перед вами система, в которой выполняется закон сохранения импульса.
Задача на закон сохранения импульса
Для закрепления темы на закон сохранения импульса лучше всего выполнить практическую задачу.
Задача: снаряд, который летел в горизонтальном направлении со скоростью v, разрывается на два осколка массой m1 и m2 каждый. Скорость осколка массой m1 равна v1 и направлена вертикально вверх. Необходимо определите модуль и направление скорости осколка массой m2.
Для решения этой задачи подойдет такой рисунок:
Где:
• m1 + m2 – это изначальная масса снаряда со скоростью v, и он летит горизонтально вправо;
• m1 – осколок, который летит со скоростью v1 вертикально вверх;
• m2 – это осколок, который движется в некотором направлении со скоростью v2, и эту скорость нам и надо найти, а в качестве направления движения необходимо найти угол α.
Итак, что же нам дано по условию задачи: m1, m2, начальная скорость снаряда v и скорость осколка v1.
А необходимо найти: угол α и скорость v2.
Для решения этой задачи необходимы две вещи:
• во-первых, необходимо задать координатные оси х и у;
• во-вторых, воспользоваться законом сохранения импульса.
Закон сохранения импульса говорит нам о том, что импульс некоторой системы в состоянии «до» точно такой же, как и импульс этот же самой системы в некотором состоянии «после».
В данном случае импульс один и тот же после разрыва снаряда. А так как кроме снаряда в нашей задаче больше не присутствуют никакое постороннее тело, то данную систему можно рассматривать, как замкнутую. А значит, в ней будет выполняться закон сохранения импульса.
Давайте запишем начальный импульс системы. До взрыва импульс системы был равен:
После взрыва системы в горизонтальном направлении х движется только отрезок m2. Значит импульс системы по оси ОХ будет равен:
А по оси ОY окажется, что начальный импульс системы равен 0, а конечный импульс системы будет равен:
В результате мы получаем систему, состоящую из двух уравнений:
Для того, чтобы было легче ее решить, перенесем влево все, что относиться к массе m2 и скорости v2, а вправо все остальное:
Теперь если поделить второе уравнение на первое, то получится, что слагаемые m2v2 сократятся, и в левой части окажется тангенс угла α.
И, исходя из этого уравнения, можно найти размер угла α.
Соответственно часть задачи, которая относится к определению направления, решена.
Теперь необходимо найти модуль значения для скорости v2.
Для этого необходимо возвести в квадрат первое и второе уравнения и сложить их вместе, в результате получим:
Слева мы получаем не что иное, как основное тригонометрическое тождество с множителем m2v2 в квадрате, а справа мы получим:
Теперь необходимо выразить с левой части v2, чтобы получить ответ на задачу:
Вот такое значение скорости получается для второго осколка.
Соответственно ответами на задачу такие:
И
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Закон сохранения импульса
Закон сохранения импульса
Импульс замкнутой системы, состоящей из (n), тел остается постоянным с течением времени при любых взаимодействиях тел внутри данной системы
[displaystylesum_{i=1}^{n}vec{p}_i=displaystylesum_{i=1}^{n}m_ivec{v}_i=const]
Охотник, стоящий на гладком льду, стреляет из ружья. Масса заряда (0,05 text{кг} ). Скорость снаряда (200 text{м/c}). Какова масса охотника, если его скорость после выстрела равна (0,1 text{м/c})
Так как до выстрела общий импульс системы равен нулю. По Закону Сохранения импульса: [m_1cdot upsilon_1 — m_2cdot upsilon_2 = 0] Где (m_2) – масса охотника, (m_1) – масса снаряда (v_1), (upsilon_2) – скорости снаряда и охотника соответственно [m_2 = frac {m_1 cdot upsilon_1} {upsilon_2}] [m_2= frac {0,05 text {кг} cdot 200 text{ м/с}}{0,1 text{м/c} } =100text{ кг}]
Ответ: 100
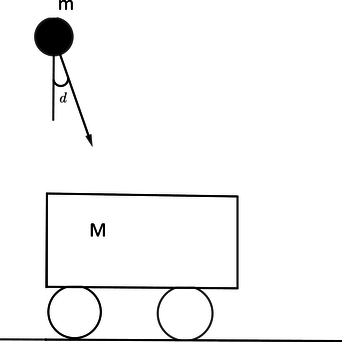
Камень массой (m =4 text { кг} ) падает под углом (alpha=30^circ) к вертикали со скоростью (10 text { м/с}) в тележку с песком общей массой ( M= 16 text { кг}), покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в неё камня.
В начале импульс тележки равен нулю. по Закону Сохранения Импульса(на горизонтальную ось): [m_1cdot upsilon_1sinalpha=(m+M)cdotupsilon’] [upsilon’=frac{m_1cdot upsilon_1sinalpha}{m+M}] [upsilon’=frac{4text{ кг}cdot 10text{ м/с} cdotdfrac 1 2 }{4text{ кг}+16text{ кг}}=1text{ м/c}]
Ответ: 1
С неподвижной лодки массой (M=50text{ кг } ) на берег прыгнул мальчик массой (m=40text{ кг } ) со скоростью (upsilon_1 = 1 text{ м/c } ) относительно берега, направленной горизонтально. Какую скорость (upsilon_2) относительно берега приобрела лодка?
Начальный импульс системы равен нулю. По закону Сохранения Импульса: [Mcdotupsilon_2-mcdotupsilon_1 = 0] [upsilon_2=frac{mcdotupsilon_1}{M}] [upsilon_2=frac{40 text{ кг }cdot 1 text{ м/с } } {50 text{ кг}} =0,8 text{ м/c }]
Ответ: 0, 8
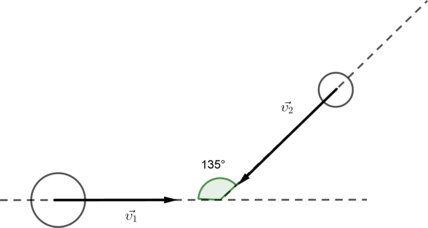
Одинаковые шары массой (m = 1 text{ кг } ) каждый движутся со скоростями, направления которых указаны на рисунке, и сталкиваются. Чему будет равен суммарный импульс шаров после столкновения, если (upsilon_1=16 text{ м/c }), а (upsilon_2=upsilon_1 cdot sqrt{2})?
Из рисунка видно, что углы между осями и вторым шаром равны (45^circ). По закону сохранения импульса суммапрный импульс системы до удара и после удара будет одинаковый. Найдем проекции суммарного импульса на каждую ось: (p_x’) – Суммарный импульс на ось Ox (p_y’) – суммарный импульс на ось Oy [p_{2x}-p_{1x}=p_x’] [p_{2y}-p_{1y} =p_y’] По рисунку (p_{1y}=0) По теореме Пифагора: [P_{text{итог}}’=sqrt{p_y’^2+p_x’^2}] Заменим (upsilon_2) на (upsilon_1 cdot sqrt{2} ). [p_y’=mcdotupsilon_1sqrt{2}cos{45^circ}] [p_x’=mcdot upsilon_1cdot (cos{45^circ} cdot sqrt{2}-1)] [p_y’= 1 text{кг} cdot 16 text{ м/c } cdot frac{sqrt2} 2cdot sqrt 2 = 16 frac{text{ кг }cdot text{ м }} {text{ c }}] [p_x’= 1 кг cdot 16 text{м/c} left(frac{sqrt2} {2} cdot sqrt2 — 1right)=0frac{text{ кг }cdot text{ м }} {text{ c }}] [P_{ итог } = sqrt{left(16frac{text{кг}cdot text{м}} { c}right)^2}=16frac{text{ кг }cdot text{ м }} { text{ c } }]
Ответ: 16
На неподвижный бильярдный шар налетел другой такой же. После удара шары разлетелись под углом (90^circ) так, что импульс одного равен (p_1=5dfrac {text{ кг }cdot text{ м }} {text{ c }} ), а другого (p_2 = 12dfrac{text{ кг }cdot text{ м }}{text{ c }}) (см.рисунок). Чему был равен импульс налетающего шара?
По закону сохранения импульса: [vec{p’}=vec{p_1}+vec{p_2}] Так как шары разлетелись под углом (90^{circ}), применим теорему Пифагора: [p’=sqrt{p_1^2 + p_2^2}] [p’=sqrt{left(5 frac {text{ кг }cdot text{ м }} {text{ c }} right)^2 + left(12frac {text{ кг }cdot text{ м }} {text{ c }} right)^2}=13frac {text{ кг }cdot text{ м }} {text{ c }}]
Ответ: 13
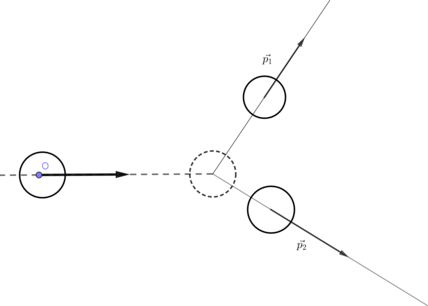
По гладкой горизонтальной плоскости по осям Оx и Оy движутся две шайбы с импульсами равными по модулю (p_1 =3 ) кг(cdot)м/с и (p_2 =6 ) кг(cdot)м/с (см.рисунок). После их соударения вторая шайба продолжает двигаться по оси y в прежнем направлении. Модуль импульса первой шайбы после удара равен (p_1’= 5 ) кг(cdot)м/с. Найдите модуль импульса второй шайбы после удара.
Запишем ЗСИ (закон сохранения импульса): [vec{p_1}+vec{p_2}=vec{p_1}’+vec{p_2}’ quad(1)] Спроецируем данное уравнение на ось Оx: [p_1=p_{1x}’ quad(2)] Спроецируем на ось Оy: [p_2=p_{1y}’+p_2′ quad(3)] После удара импульс первой шайбы стал равен [p_1’=sqrt{p_{1x}^{prime 2}+p_{1y}^{prime 2}} quad(4)] Из (2) следует, что (p_{1x}’ =3 ) кг(cdot)м/с. Из (4) следует, что [p_{1y}=sqrt{p_1^{prime 2}- p_{1x} ^{prime 2}}=sqrt{25-9} = 4 text{ кг$cdot$м/c}]
Найдем (p_2′) из (3): [p_2’=p_2-p_{1y}’= 6 — 4 = 2text{ кг·м/c}]
Ответ: 2
Снаряд, выпущенный вертикально вверх, мгновенно разрывается в высшей точке траектории на два осколка, массы которых (m) и (4m). Скорость лѐгкого осколка сразу после взрыва (upsilon_1=500) м/с. Найдите скорость (upsilon_2) второго осколка сразу после взрыва.
Суммарный импульс снаряда до взрыва равен 0 (так как взрыв происходит в наивысшей точки траектории), следовательно сразу после взрыва суммарный импульс тоже равен 0: [0=vec{p_1}+vec{p_2}] где (p_1) и (p_2) – это импульс первого и второго осколка. Найдем скорость второго осколка: [mupsilon_1=4mupsilon_2] [upsilon_2=frac{upsilon_1}{4}=frac{500}{4}=125 text{ м/с}]
Ответ: 125
Тема: Какова скорость второго осколка? (Прочитано 6082 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Снаряд, летевший с горизонтальной скоростью υ = 600 м/с, разрывается на 2 осколка. Масса одного осколка в 2 раза больше массы другого. Больший осколок падает по вертикали, а меньший – под углом α = 30 градусов к горизонту. Какова скорость второго осколка? Сделать рисунок.
« Последнее редактирование: 28 Декабря 2014, 16:20 от Сергей »
Записан
Решение. Для решения задачи используем закон сохранения импульса, покажем рисунок.
[ (m+M)vec{upsilon }=mcdot {{vec{upsilon }}_{1}}+Mcdot {{vec{upsilon }}_{2}} (1). ]
М = 2∙m (2).
Найдем проекции на ось оХ и оY:
[ begin{align}
& oX: (m+M)upsilon =mcdot {{upsilon }_{1}}cdot cos alpha (3), \
& oY: 0=mcdot {{upsilon }_{1}}cdot sin alpha -Mcdot {{upsilon }_{2}} (4). \
end{align} ]
Подставим (2) в (3) и выразим скорость первого осколка.
[ 3cdot mcdot upsilon =mcdot {{upsilon }_{1}}cdot cos {{30}^{0}}, {{upsilon }_{1}}=frac{3cdot upsilon }{cos {{30}^{0}}}.
]
υ1 = 2081,0 м/с.
Подставим υ1 и (2) в (4) выразим скорость второго осколка.
[ 2cdot mcdot {{upsilon }_{2}}=mcdot {{upsilon }_{1}}cdot sin alpha , {{upsilon }_{2}}=frac{{{upsilon }_{1}}cdot sin alpha }{2}. ]
υ2 = 520,25 м/с.
Ответ: 2081,0 м/с, 520,25 м/с.
« Последнее редактирование: 07 Января 2015, 11:45 от alsak »
Записан