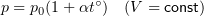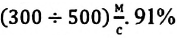Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.
Виды скоростей молекул газа
Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.
Средняя (или среднеарифметическая) скорость определяется уравнением
v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}
где viv_i – скорость ii-й молекулы;
nn –количество молекул.
Средняя квадратичная скорость определяется как:
vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}
По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.
Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,
vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}
Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.
Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.
Экспериментальное определение скоростей газовых молекул
Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.
В других опытах использовали также висмут, кадмий, цезий.
Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s1 и s2 проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.
Рис. 1
На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а1. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с-1.
При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,
t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}
где vv – скорость атомов серебра.
Отсюда
v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}
Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением
(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}
что согласуется со средней скоростью молекул, которые определяются по формуле
v=8kTπmv=sqrt{frac{8kT}{pi m}}
Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.
Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).
Рис. 2
Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.
Тест по теме «Скорость движения молекул»
Скорость молекул идеального газа
Средняя скорость молекул идеального газа (или средняя квадратичная скорость молекул) вычисляется по формулам, описанным ниже, и измеряется в м/с.
Формула скорости молекул газа
По формуле средней квадратичной скорости молекул вычисляется и скорость молекул идеального газа (v):

где R – универсальная газовая постоянная, равная 8,31, Дж/К•моль;
Т – температура, К;
М – молярная масса, кг/моль;
k – постоянная Больцмана, равная 1,38*10-23, Дж/К;
m – масса одной молекулы идеального газа, кг.
Известно, что молярная масса М равна произведению массы молекулы на число Авогадро 6,02*1023 (моль-1) , т.е. М = Nam.
Скорость молекул газа вычисляется в м/с.
Следовательно, скорость частичек газа зависит от температуры и их массы. Чем выше температура, тем быстрее движутся молекулы газа, а чем они тяжелее, тем медленнее их скорость.
Что такое идеальный газ
Идеальным считается настолько разряженный газ, что в нем можно пренебречь взаимодействием между молекулами. Иными словами в таком газе молекул настолько мало, что между ними почти не происходит столкновений и взаимного притяжения.
При небольшом давлении и не самой низкой температуре обычные газы близки к идеальному состоянию. Например, водород и кислород в обычных условиях можно считать идеальными газами.
Скорость молекул некоторых газов в обычных условиях приведены в таблице:

Измерение скоростей газовых молекул. Опыт Штерна. Распределение Максвелла
Из формул (~mathcal h W_K mathcal i = frac 32 kT) и (~mathcal h W_K mathcal i = frac{m_0 mathcal h upsilon^2 mathcal i}{2}) получаем формулу для расчета средней квадратичной скорости движения молекул одноатомного газа:
(~mathcal h upsilon_{KB} mathcal i = sqrt{mathcal h upsilon^2 mathcal i} = sqrt{frac{3kT}{m_0}} = sqrt{frac{3RT}{M}} , qquad (1))
так как (~m_0 = frac{M}{N_A}) и (~kN_A = R), где R — универсальная газовая постоянная.
Таким образом (~mathcal h upsilon_{KB} mathcal i) зависит от температуры и природы газа. Так, при 0 °С для водорода она равна 1800 м/с. для азота — 500 м/с.
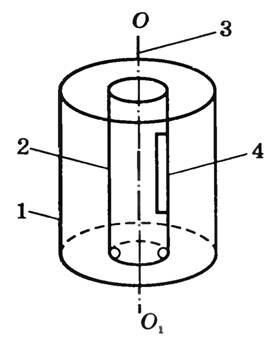
Впервые на опыте определил скорость молекул О. Штерн. В камере, из которой откачан воздух, находятся два коаксиальных цилиндра 1 и 2 (рис. 1), которые могут вращаться вокруг оси OO1 с постоянной угловой скоростью ω.
Рис. 1
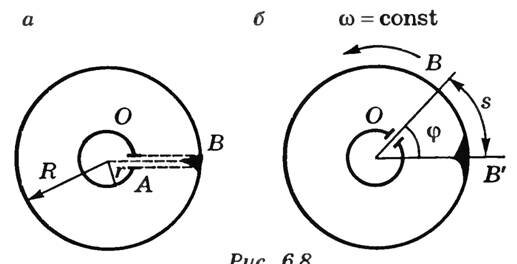
Вдоль оси OO1 натянута платиновая посеребренная проволока, через которую пропускают электрический ток. Она нагревается, и серебро испаряется. Атомы серебра через щель 4 в стенке цилиндра 2 попадают в цилиндр 1 и оседают на его внутренней поверхности, оставляя след в виде узкой полоски, параллельной щели. Если цилиндры неподвижны, то полоска расположена напротив щели (точка В на рис. 2, а) и имеет одинаковую толщину.
Рис. 2
При равномерном вращении цилиндра с угловой скоростью ω полоска смещается в сторону, противоположную вращению, на расстояние s относительно точки В (рис. 2, б). На такое расстояние сместилась точка В цилиндра 1 за время t, которое необходимо, чтобы атомы серебра прошли расстояние, равное R — r, где R и r — радиусы цилиндров 1 и 2.
(~s = upsilon_1 t = omega Rt ,)
где υ1 — линейная скорость точек поверхности цилиндра 1. Отсюда
(~t = frac{s}{omega R} .)
Скорость атомов серебра
(~upsilon = frac{R — r}{t} = frac{omega(R — r)R}{s} .)
Зная R, r, ω и измерив экспериментально s, по этой формуле можно рассчитать среднюю скорость движения атомов серебра. В опыте Штерна υ ~ 650 м/с. Это значение совпадает с теоретическим значением средней квадратичной скорости молекул. Это служит экспериментальным доказательством справедливости формулы (1), а следовательно, и формулы (3).
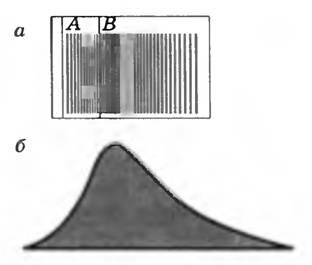
В опыте Штерна было обнаружено, что ширина полоски на поверхности вращающегося цилиндра гораздо больше геометрического изображения щели и толщина ее в разных местах неодинакова (рис. 3, а). Это можно объяснить только тем, что атомы серебра движутся с различными скоростями. Атомы, летящие с некоторой скоростью, попадают в точку В’. Атомы, летящие быстрее, попадают в точку, лежащую на рисунке 2 выше точки В’, а летящие медленнее, — ниже точки В’. Таким образом, каждой точке изображения соответствует определенная скорость, которую достаточно просто определить из опыта. Этим и объясняется то, что толщина слоя атомов серебра, осевших на поверхности цилиндра, не везде одинакова. Наибольшая толщина в средней части слоя, а по краям толщина уменьшается.
Рис. 3
Изучение формы сечения полоски осевшего серебра с помощью микроскопа показало, что она имеет вид, примерно соответствующий изображенному на рисунке 3, б. По толщине отложившегося слоя можно судить о распределении атомов серебра по скоростям.
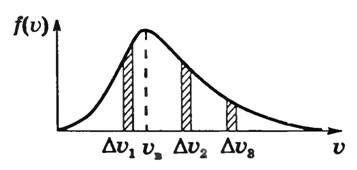
Разобьем весь интервал измеренных на опыте скоростей атомов серебра на малые Δυ. Пусть υ — одна из скоростей этого интервала. По плотности слоя подсчитаем число ΔN атомов, имеющих скорость в интервале от υ до υ + Δυ, и построим график функции (~f(upsilon) = frac{Delta N}{N Delta upsilon}) , где Ν — общее число атомов серебра, осевших на поверхности цилиндра. Получим кривую, изображенную на рисунке 4. Она называется функцией распределения молекул по скоростям.
Рис. 4
Площадь заштрихованной площадки равна (~frac{Delta N}{N Delta upsilon} Delta upsilon = frac{Delta N}{N}) , т.е. равна относительному числу атомов, имеющих скорость в пределах υ + Δυ. Мы видим, что числа частиц, имеющих скорость из разных интервалов υ1 + Δυ1, υ2 + Δυ2, υ3 + Δυ3, резко различны. Существует какая-то скорость, около значения которой находятся скорости, с которыми движется наибольшее число молекул. Она называется наиболее вероятной скоростью υB, и ей соответствует максимум на рисунке 4. Эта кривая хорошо соответствует кривой, полученной Дж. Максвеллом, который, пользуясь статистическим методом, теоретически доказал, что в газах, находящихся в состоянии термодинамического равновесия, устанавливается некоторое, не меняющееся со временем, распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону, графически изображаемому кривой f(υ). Наиболее вероятная скорость, как показал Максвелл, зависит от температуры газа и массы его молекул по формуле (~mathcal h upsilon_B mathcal i = sqrt{frac{2RT}{M}}).
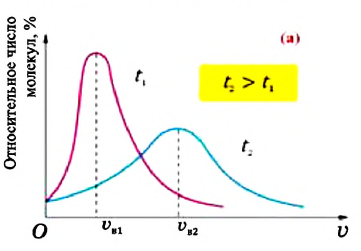
Такому распределению подчиняются молекулы всевозможных веществ в различных состояниях при данной температуре. Если увеличить температуру (T2 > T1), то кривая (рис. 5) сместится вправо, наиболее вероятная скорость возрастет, появится больше быстрых частиц, уменьшится число медленных частиц и даже тех, которые движутся со скоростями, близкими к наиболее вероятной. Площади под кривыми будут одинаковыми, так как общее число частиц N не изменяется.
Зная закон изменения функции распределения молекул по скоростям f(υ), можно рассчитать среднюю, или среднюю арифметическую, скорость молекулы:
(~mathcal h upsilon mathcal i = frac 1N int upsilon dN = int^{infty}_0 upsilon F(upsilon) d upsilon .)
Подставляя сюда значение F(υ) и интегрируя (в виду сложности F(υ) мы ее не приводим), получают
(~mathcal h upsilon mathcal i = sqrt{frac{8kT}{pi m_0}} = sqrt{frac{8RT}{pi M}} .)
Среднее значение квадрата скорости
(~mathcal h upsilon^2 mathcal i = frac 1N int upsilon^2 dN = int^{infty}_0 upsilon^2 F(upsilon) d upsilon .)
Средняя квадратичная скорость
(~mathcal h upsilon_{KB} mathcal i = sqrt{mathcal h upsilon^2 mathcal i} = sqrt{frac{3RT}{M}} .)
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 134-136.
Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества
m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;

1.3 Средняя квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа
1.5 Давление идеального газа
n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта
p — давление;
V — объем газа.
1.7 Закон Шарля
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака
V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона
1.10 Объединенный закон газового состояния (уравнение Клапейрона)
1.11 Закон Дальтона
pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа
ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV
p — давление газа.
При изменении объема от V1 до V2
2.3 Первый закон термодинамики
ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа
ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Преподаватель который помогает студентам и школьникам в учёбе.
Скорость движения молекул газа — формулы и определение с примерами
Определение скорости движения молекул газа:
Молекулы газа находятся в непрерывном хаотичном движении. Удивительно то, что беспорядочное движение огромного числа молекул газа подчиняется определенной закономерности распределения по скоростям. в таблице 6.2 дано распределение по скоростям для молекул азота (при комнатной температуре и в процентах относительно общего количества молекул).
Из таблицы видно, что 1% от общего числа молекул движется с очень малыми скоростями. Приблизительно половина всех молекул (42%) движется со средними скоростями
- Заказать решение задач по физике
В 1860 году английский физик Джеймс Максвелл (1831-1879), используя теорию вероятности, определил закономерность распределения молекул газа по скоростям и изобразил ее графически (а). Максимум графика соответствует наиболее вероятному значению скорости 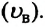
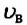
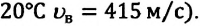
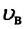
Первые экспериментальные исследования по измерению скоростей молекул газа провел в 1920 году немецкий ученый Отто Штерн (1888-1969). Вычисленные им значения для скоростей молекул совпали со значениями, определенными на основе MKT. Научное значение опытов Штерна состоит в том, что скорость молекул газа была определена экспериментально, и в том, что эти опыты подтвердили теоретически установленную закономерность распределения молекул газа по скоростям.
- Газовые законы
- Взаимодействие молекул
- Агрегатное состояние вещества
- Зависимость размеров тел от температуры
- Строение вещества в физике
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Движение молекул в физике в газах, жидкостях и твёрдых телах