Как найти скорость в электростатике

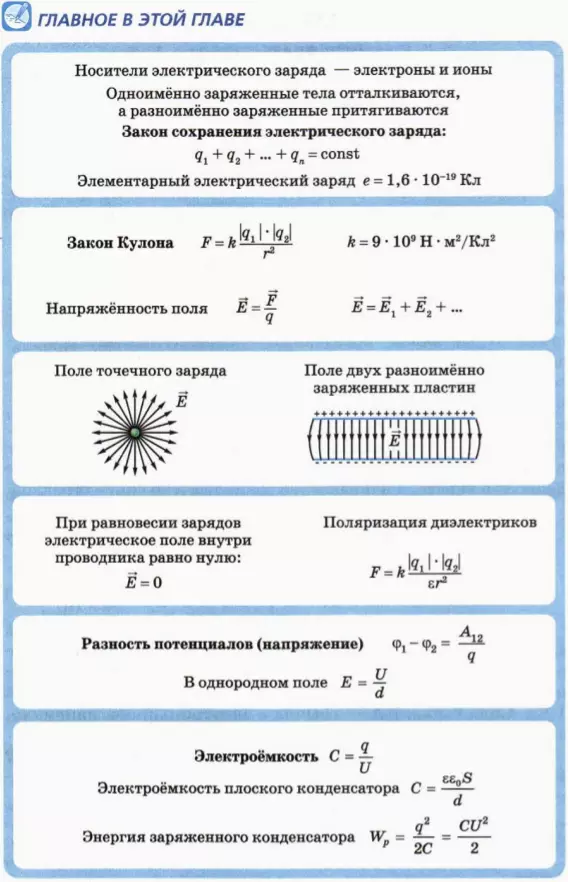
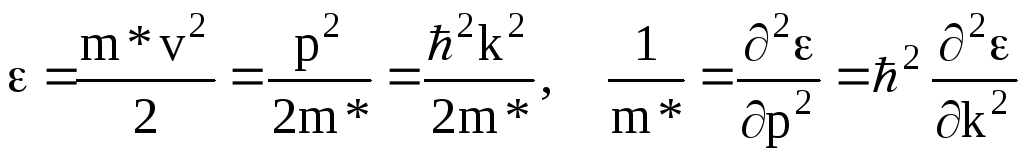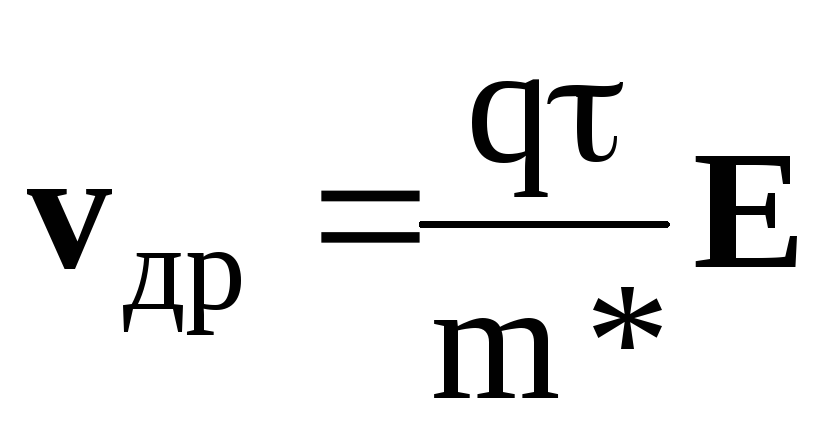Электрон из состояния
покоя разгоняется в однородном электростатическом поле, модуль напряженности
которого 3,0 МВ/м. Определите модуль скорости электрона через 1,0 нс после
начала движения.

Решение.

В качестве физической
системы рассмотрим электрон. Если пренебречь взаимодействием электрона с
гравитационным, электрическим и магнитными полями Земли, а также предположить,
что он движется в вакууме, то разгон происходит только под действием
ускоряющего поля.

Поэтому движение электрона в инерциальной системе отсчета
можно описать вторым законом Ньютона и кинематическими законами
равноускоренного прямолинейного движения.

В качестве тела отсчета
возьмем лабораторию, ось OX направим в сторону
движения (т.е. против поля), выбрав начало координат в точке, из которой
электрон начал двигаться. Если спроецировать векторы, изображающие
соответствующие величины, на ось OX, с учетом того, что v₀ = 0, получим:

ma
= eE, x = at²/2, v = at.

Откуда искомая скорость
v = eEt/m.

Подставив числовые
значения заряда и массы электрона, а также значения E и t, получим v = 5,3•10⁸ м/с,
что больше скорости света в вакууме.

Так как ни в какой
системе отсчета тело не может двигаться со скоростью превышающей скорость света
в вакууме, то полученное значение скорости не может быть ответом задачи. Причиной
ошибки явилось неявно сделанное предположение о том, что движение электрона
может быть описано законами классической механики.

Изменение импульса тела
равно импульсу силы, действующей на него, т.е. Dp = FDt, не только в
классической, но и в релятивистской механике. Причем пот релятивистских
скоростях движения импульс тела p = gmv.

С учетом этого,
применительно к ситуации, описанной в задаче, теорему об изменении импульса
можно записать в виде: D(gmv)=eEDt.

Принимаем во внимание,
что Dv = v –
v₀ = v, Dt = t – t₀ = t (т.е. в момент времени t₀ = 0 скорость v₀ = 0).

Откуда находим модуль
искомой скорости электрона v.

Ответ: v = 2,6•10⁸ м/с.

Источник: Физика. Полный курс подготовки к ЦТ.  Под общей редакцией проф. В.А. Яковенко.

Условие задачи:

Найти скорость, которую приобретает электрон, пролетевший в электрическом поле от точки с потенциалом 100 В до точки с потенциалом 300 В, если начальная скорость электрона равна 5 Мм/с.

Задача №6.3.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(varphi_1=100) В, (varphi_2=300) В, (upsilon_0=5) Мм/с, (upsilon-?)

Решение задачи:

Работу электрического поля (A) при перемещении электрона из точки с потенциалом (varphi_1) до точки с потенциалом (varphi_2) необходимо определять по формуле:

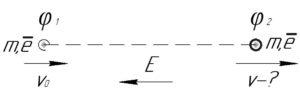
[A = – Delta varphi e]

В этой формуле (Delta varphi) – разность потенциалов, равная (Delta varphi = {varphi _1} – {varphi _2}), (e) – модуль заряда электрона (элементарный заряд), равный 1,6·10^-19 Кл. Знак “минус” появился из-за того, что электрон имеет отрицательный заряд. Тогда:

[A = – left( {{varphi _1} – {varphi _2}} right)e]

[A = left( {{varphi _2} – {varphi _1}} right)e;;;;(1)]

Работа электрического поля также равна изменению кинетической энергии электрона:

[A = frac{{m{upsilon ^2}}}{2} – frac{{mupsilon _0^2}}{2}]

[A = frac{m}{2}left( {{upsilon ^2} – upsilon _0^2} right);;;;(2)]

Масса электрона (m) равна 9,1·10^-31 кг. Приравняем (1) и (2), тогда:

[left( {{varphi _2} – {varphi _1}} right)e = frac{m}{2}left( {{upsilon ^2} – upsilon _0^2} right)]

[{upsilon ^2} – upsilon _0^2 = frac{{2left( {{varphi _2} – {varphi _1}} right)e}}{m}]

[upsilon = sqrt {upsilon _0^2 + frac{{2left( {{varphi _2} – {varphi _1}} right)e}}{m}} ]

Задача решена в общем, теперь подставим в формулу численные значения и посчитаем ответ:

[upsilon = sqrt {{{left( {5 cdot {{10}^6}} right)}^2} + frac{{2 cdot left( {300 – 100} right) cdot 1,6 cdot {{10}^{ – 19}}}}{{9,1 cdot {{10}^{ – 31}}}}} = 9,76 cdot {10^6};м/с]

Ответ: 9,76·10⁶ м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.48 Энергия 100 эВ в системе СИ равна
6.3.50 В углах квадрата со стороной 4 см поместили 4 электрона. Под действием электрических
6.3.51 Электрон, ускоренный разностью потенциалов 5 кВ, влетает в середину зазора между

1.2.5. Зависимость скорости электрона от напряженности электрического поля. Понятия эффективной массы и подвижности.

электрический ток в образце зависит не
только от концентрации носителей заряда,
но и от скорости с которой они переносятся
под действием электрического поля.
После того как мы научились рассчитывать
концентрацию свободных носителей в
твердом теле рассмотрим как ведут себя
носители заряда в кристалле при наложении
на него электрического поля.

Рассмотрение начнем с поведения
единичного свободного заряда в нейтральной
не взаимодействующей с зарядом среде
(допустим в вакууме) при наличии
электрического поля E,
которое накладывается на среду в моментt=0. Электрическое поле
приводит к возникновению силы
электростатического взаимодействияF, под действием которой
электрон начнет ускоряться.

,
(1.25)

где q,m–
заряд и масса электрона,vиaего скорость и ускорение.
Таким образом в электрическом поле
заряженная частица разгоняется с
постоянным ускорением пропорциональным
напряженности электрического поля и
обратно пропорциональным ее массе. При
этом энергия частицы будет изменяться
со временем по квадратичному закону
относительно импульса частиц или ее
волнового вектораk(p=
ћk, где ћ =h/(2π),
h – постоянная Планка).

(1.26)

Поскольку приобретаемая заряженной
частицей энергия не зависит от направления
электрического поля зависимость (1.5)
симметрична относительно импульса и
волнового вектора (это параболоид
выпуклость которого определяется массой
частицы).

Измерив зависимость энергии частицы
от импульса (или волнового числа мы
можем ) используя (1.5) определить
эффективную массу. Действительно дважды
продифференцировав (1.5) получим.

(1.27)

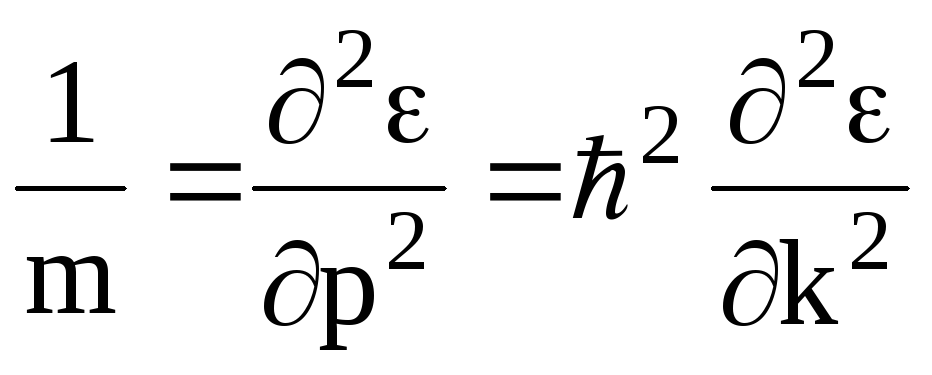
Предположим, что на частицу действует
некоторая тормозящая сила F*
о существовании которой мы не знаем.
Тогда уравнение (1.4) можно переписать в
следующем виде:

(1.28)

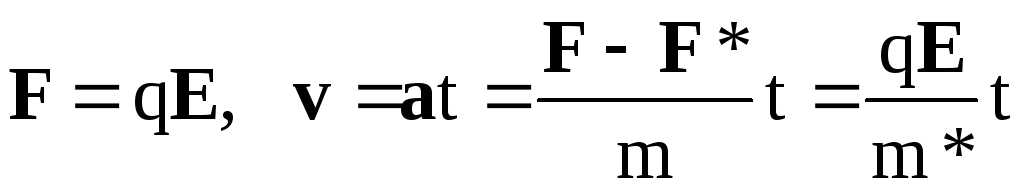
Соответственно, если для определения
массы электрона (или любой другой
заряженной частицы) в некоторой
взаимодействующей с частицей среде
воспользуемся формулой (1.6), то вместо
массы электрона будет рассчитана
некоторая другая величина, которую
будем назвать эффективной массой
электрона в данной среде.

_(1.29)

Поскольку при движении электронов (или
других заряженных частиц) в твердом
теле внутренние поля неизвестны, то их
характеристики используют понятие
эффективной массы.

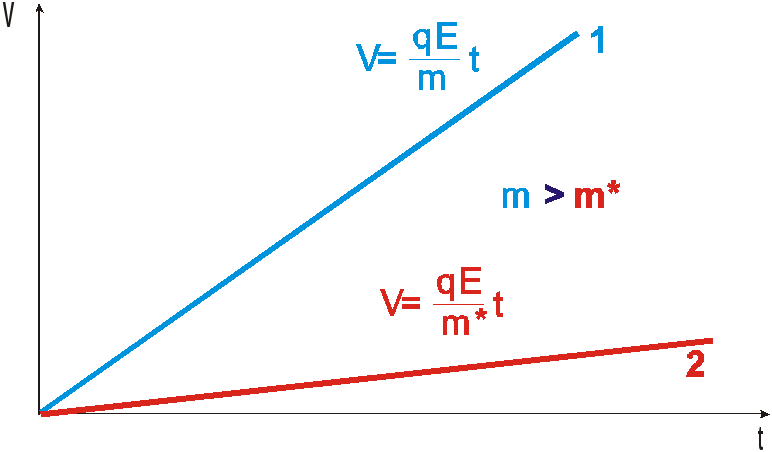
Рис.
1.18. Изменение скорости заряженной
частицы в электрическом поле, при
отсутствии взаимодействия со средой(1)
и при торможении частицы средой.

На рис. 1.5 показано как будет со временем
изменяться скорость свободной частицы
в электрическом поле, в соответствии с
(1.4) и (1.7 ). Эти формулы справедливы для
случая, когда заряженная частица не
испытывает столкновений и в соответствии
с ними частицу можно разогнать
электрическим полем до бесконечной
энергии. Именно этот принцип был
использован в первых линейных ускорителях
элементарных частиц.

По мере разгона частицы возрастает ее
импульс и соответствующее ему волновое
число (величина, характеризующая величину
волнового вектора). На рис. 1.6. показаны
соответствующие зависимости изменения
энергии частицы от величины волнового
числа (импульса).

Рис.
1.19. Зависимости энергии свободных
зарядов от величины их волнового числа
(импульса).

Как видно из рис. 1.18. и рис. 1.19 набираемая
в электрическом поле энергия частицы
зависит от скорости частицы (волнового
числа) и массы. Поскольку выпуклость
кривой характеризуется ее второй
производной можно сделать вывод, что
чем меньше эффективная масса частицы,
тем больше выпуклость, см. (1.27) и (1.29).

В кристалле энергия электрона (дырки)
в разрешенной зоне не может превысить
значение потолка разрешенной зоны,
следовательно импульс и волновой вектор
так же имеют ограничения, причем
максимальное значение волнового числа
должно быть кратно постоянной решетки.
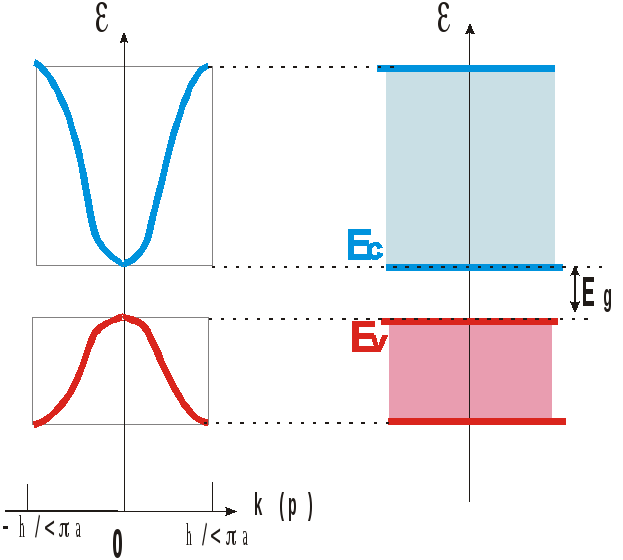
На рис. 1.20 показана рассчитанное изменение
энергии электрона от величины волнового
числа (значения) импульса для кубического
кристалла.

Рис. 1.20. Зависимость энергии от волнового
числа (импульса) в кристалле (a– постоянная решетки вдоль заданного
направления)

Из рисунка видно, что в электронном
представлении у потолка валентной зоны
знак эффективной массы изменяется
(должно происходить отражение частицы).
Следует отметить, что у дна зоны
проводимости энергия имеет параболическую
зависимость от импульса (волнового
числа):

(1.31)

Если вести отсчет от дна зоны проводимости
E_c=
0, то зависимость энергии электрона от
импульса (волнового вектора) будет такая
же как для свободного электрона см.
(1.26). Это дает нам основание рассматривать
электроны в зоне проводимости, находящиеся
вблизи дна зоны проводимости как
свободные частицы (иногда говорят
квазисвободные или квазичастицы), считая
что они подчиняются тем же закономерностям,
что и свободные частицы, но отличаются
от них величиной эффективной массы,
которую вблизи дна зоны можно считать
постоянной (пока выполняется параболическое
приближение).

Аналогичный подход справедлив и для
дырки. Вводя дырку мы переходим от
электронного представления к дырочному,
т.е. мы принимаем, то масса дырки
положительная, а заряд отрицательный
и энергия ее отсчитывается от потолка
валентной зоны к ее дну, тогда дырка
будет вести себя так же как электрон у
потолка валентной зоны. При этом энергия
дырки у потолка валентной зоны так же
изменяется по параболическому закону
как и для электрона:

(1.32)

Таким образом дырку, находящуюся потолка
валентной зоны так же можно рассматривать
как свободную частицу.

В реальной жизни электрон в электрическом
поле не может набирать энергию до
бесконечности, рано или поздно он
столкнется с другой частицей и отдаст
ей накопленную энергию. Вероятность
столкновений частиц в газах и твердых
телах характеризуется временем или
длиной их свободного пробега. Эти же
величины характеризуют движение
носителей заряда в твердом теле.

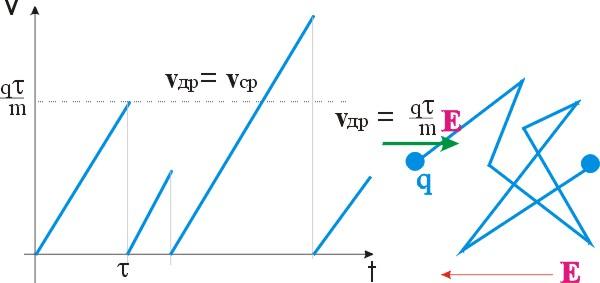
Схема, приведенная на рис. 1.21 показывает
изменение скорости электрона в образце,
к которому приложено напряжение и
поясняет физический смысл подвижности.
Электрон участвует в хаотическом
тепловом движении, причем в различные
моменты времени его скорость имеет
случайное направление так что смещение
его в любом направлении равновероятно.
В электрическом поле электрон приобретает
дополнительную скорость под действием
поля, так что продолжая участвовать в
тепловом движении он постепенно смещается
под действием поля. Средняя скорость
тем выше, чем больше длина свободного
пробега и чем меньше эффективная масса
частицы.

Рис.
1. 21. Диаграмма, поясняющая движение
электрона в твердом теле

Поскольку электрон набирает энергию в
поле за время свободного пробега и
отдает ее при столкновении с решеткой
или другими носителями заряда, то
средняя скорость, которую приобретают
носители в направлении поля, будем
называть ее скоростью дрейфа зарядов
v_дрдолжна
зависеть от средней длины свободного
пробега τ.

_(1.36)

_{Коэффициент пропорциональности
между дрейфовой скоростью и напряженностью
электрического поля обычно называют
подвижностью носителей заряда
и обозначают μ:}

_{μ =
qτ/m*
(1.37)}

_{Как видно из (1.36) и (1.37) подвижность
имеет размерность в системе СИ м}²_{/(Вс)
, широко так же используются значения
подвижности с размерностью см}²_/(Вс).

_{Предположим, что ток через ток образце
создается электронами концентрация
которых n см}^-3
_{и средняя дрейфовая скорость vдр.
Поскольку величина тока равна
заряду, проходящему через сечение
образца в единицу времени можем записать:}

_{I=Sqnvдр=SqnμE
(1.38)}

Для единичной площади из (1.35) получится
уравнение для плотности тока:

_{J = qμnE
(1.39)}

_{Поскольку в дифференциальной форме
закон Ома имеет вид:}

_{J = σE,
(1.40)}

где σ – электропроводность образца
(Ом^.м или Ом^.см )

Сравнив (1.39) и (1.40) получим формулу для
электропроводности:

σ = qμn(1.41)

Если электрический ток создается
различными носителями (всего Nтипов) с концентрацией каждого типаn_i
, то:

(1.42)

таким борзом мы видим, что проводимость
материала определяется двумя основными
параметрами: подвижностью носителей
заряда и их концентрацией.

Величина подвижности пропорциональна
длине свободного пробега, которая
зависит от частоты столкновений носителей
заряда с решеткой или атомами примеси.
Поскольку при столкновениях носители
отдают энергию, а затем вновь набирают,
т.е. энергия носителя релаксирует, то
принято говорить о механизмах ее
релаксации. За время релаксации
принимают среднее время в течение
которого электрон полностью отдает
свою энергию.

Существует множество механизмов
рассеяния (релаксации ) энергии свободных
носителей заряда. Однако, для
полупроводников, наиболее существенные
два: рассеяние на решетки и рассеяние
на ионизованной примеси.

Для рассеяния на решетке справедливо
:

μ_r=
μ_r0T^-3/2,
(1.43)

т.е. μ_{r ~}T^-3/2и с ростом
температуры подвижность носителей
падает. Действительно длина свободного
пробега носителей заряда тем меньше,
чем сильнее колеблется решеткаl~ 1/T, для скорости носителей
справедливоv~T^1/2(mv²=3kT),
μ_r~ τ =l/v~ 1/T^3/2. Таким образом
рост, в случае если доминирует рассеяние
на решетке (примесей мало), то с ростом
температуры подвижность падает и
следовательно падает проводимость (
как это имеет место в металлах).

При рассеянии на заряженной примеси μ_i~ τ ~T^3/2.

μ_i=
μ_i0T^3/2(1.44)

Таким образом, если в образце доминирует
рассеяние на примесях, то с ростом
температуры подвижность возрастает и
соответственно возрастает проводимость.

Значения множителей μ_r0 и μ_i0зависят от химического состава материала,
наличия в нем дефектов и примесей,
степени их ионизации (для разных образцов
одного материала эти значения могут
быть различными).

При одновременном действии нескольких
механизмов рассеяния для расчета
подвижности можно воспользоваться
понятием эффективной подвижности
носителей, которая будет определяться
всеми, имеющими место механизмами
рассеяния. Для случая, когда доминирует
рассеяние на колебаниях решетки и
ионизованной примеси для эффективной
подвижности можно записать (считая, что
акты рассеяния — независимые события):

(1.45)

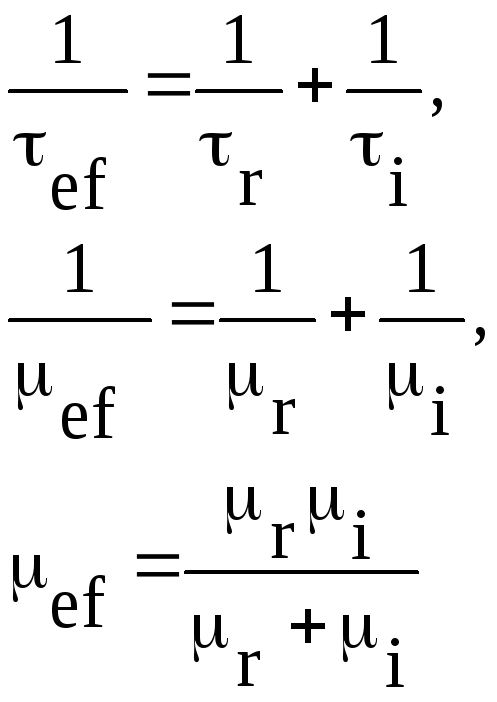
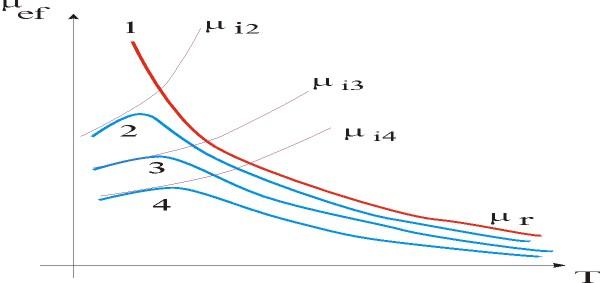
На рис. 1.21 схематически показана
зависимость эффективной подвижности
от температуры в полупроводниковом
материале с разной концентрацией
примеси. Графики построены в соответствии
с формулами (1.43) и (1.45). Кривая 1 соответствует
образцу без примесей. Кривые 2, 3, 4 образцам
с разным содержанием примеси (большему
номеру соответствует большее содержание
примеси). На этом же график приведены
соответствующие кривые для чисто
решеточного μ_rи примесного
рассеяния: μ_r2, μ_r3, μ_r4.

Характер изменения электропроводности
полупроводников с температурой, в том
случае, если не изменяется концентрация
носителей заряда будет определяться
температурной зависимостью подвижности
и зависимости будут аналогичны показанным
на рис. 2 (это может быть в примесной
области температурной зависимости
проводимости).

Рис.
1.21. Диаграмма, поясняющая температурную
зависимость подвижности μ_ef,
при рассеянии на решетке μ_rи ионизированной примеси μ_iK.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Движение вдоль линий напряженности

Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон – положительный.

? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо мала по сравнению с силой, действующей на частицу со стороны электрического поля.

? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения – прямолинейная?

Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.

? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В.
а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны?
б) Как изменилась полная энергия электрона?
в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона?
д) Какова минимальная начальная скорость электрона?

При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.

? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 10⁶ м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля.
а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку?
в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10^-9 с?
г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?

Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.

? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10^-8 с расстояние между частицами стало равным 9,8 см?
б) На какое расстояние от своей начальной точки удалился к этому моменту протон?
в) Чему равны в этот момент скорости электрона и протона?

2. Движение заряженной частицы в конденсаторе

Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.

? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?

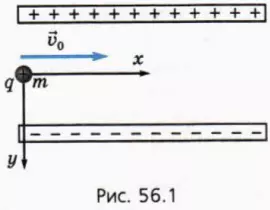
При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.

Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной. Начало координат совместим с начальным положением частицы.

? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально.
а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы?
в) Как зависят от времени координаты частицы?
г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной?
д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него?
е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?

? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 10⁷ м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор?
б) На какую пластину в таком случае попадет электрон?
в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В?
г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе?
е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?

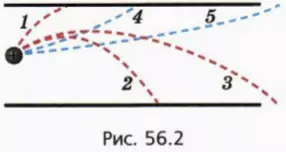
Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.

Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.

? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?

3. Движение заряженного тела в электрическом поле с учетом силы тяжести

Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.

? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора. Направим оси координат, как показано на рисунке.
56.3
а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля?
б) Чему равна проекция ускорения шарика на ось х?
в) Через какой промежуток времени шарик столкнется с пластиной? Каков знак заряда этой пластины?
г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой?
д) Какова форма траектории шарика?
е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?

Дополнительно вопросы и задания

11. Крупинка массой 10^-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально. Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10^-12 Кл.
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково?
б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?

12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле? Считайте, что силой тяжести можно пренебречь.