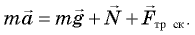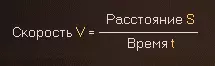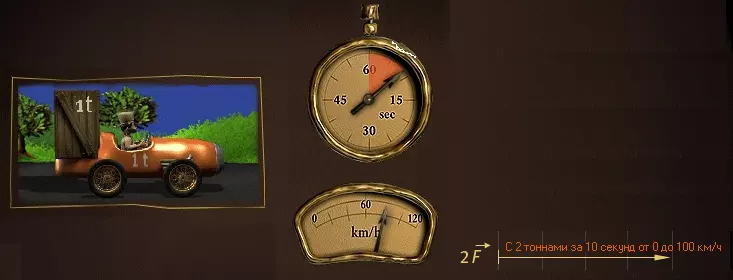Как найти мгновенную скорость в конце пути, если известны только V среднее и Vo?
В задаче не указано очень важное условие: как изменялась скорость? Попробуем решить задачу, полагая, что это было равноускоренное движение.
$S=v_ct$ (1)
$S=frac{v^2-v_0^2}{2a}$ (2)
$a=frac{v-v_0}{t}$ (3)
Подставим из (3) значение ускорения а в (2) и затем приравняем правые части (1) и (2):
$frac{v^2-v_0^2}{frac{2(v-v_0)}{2}}=v_ct$ (4)
Разность квадратов в числителе левой части (4) можно представить как произведение разности членов на их сумму. Тогда (4) принимает вид:
$frac{(v-v_0)(v+v_0)}{2(v-v_0)}=v_ct$ (5)
После сокращения получаем
$v+v_0=2v_c$ (6)
Откуда находим
$v=2v_c-v_0$
Чтобы ответить на поставленный вопрос, надо определить сначала, с каким ускорением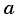 
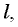
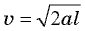
будет двигаться брусок вдоль наклонной плоскости. Зная ускорение и пройденный путь 
можно будет найти скорость бруска в конце спуска, воспользовавшись уже выведенной нами формулой для равноускоренного движения 
(см. § 3. Ускорение. Прямолинейное равноускоренное движение).
На брусок, скользящий по наклонной плоскости, действуют три силы: сила тяжести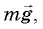 
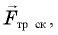
сила нормальной реакции 
и сила трения скольжения 
направленная вдоль наклонной плоскости вверх.
Чтобы найти ускорение тела, надо воспользоваться вторым законом Ньютона 
Выбирая оси координат так же, как в рассмотренном выше примере, получаем:
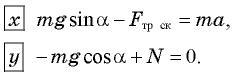
Кроме того, выполняется соотношение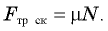 
Из второго уравнения системы следует, что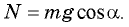 
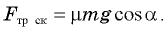
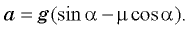
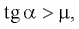
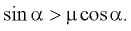
Обратите внимание: для тела, находящегося на наклонной плоскости, сила нормальной реакции меньше силы тяжести. Отсюда следует, что 
Подставляя это соотношение в первое уравнение системы, находим, что ускорение бруска 
Мы можем быть уверены в том, что это величина положительная, поскольку, согласно условию, брусок начал соскальзывать с наклонной плоскости — а это означает, в соответствии с предыдущим примером, что 
то есть 
Подставляя найденное выражение для ускорения в формулу для скорости в конце спуска, получаем 
Механика.
2014
Равномерное движение
Величина скорости показывает, какое расстояние s может преодолеть тело за определенное время t. Если машина ехала со скоростью 100 километров в час, это значит, что расстояние в 100 километров машина проехала за один час. Если эта скорость является постоянной, то мы имеем дело с равномерным движением тела.
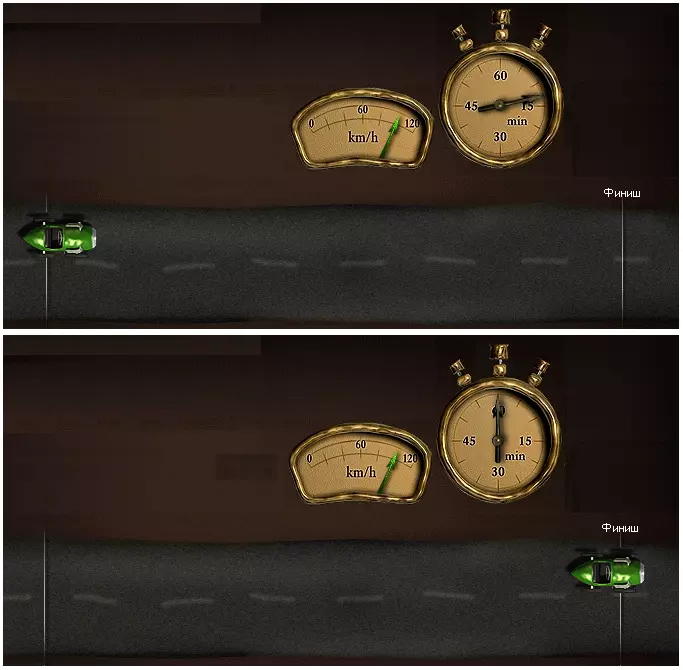
Таким образом, скорость тела определяет отношение между расстоянием s и временем t. Зная эти величины, можно легко вычислить скорость тела V. Скорость равна расстоянию, деленному на время: v = s/t.
Средняя и мгновенная скорость
Так как любая машина вряд ли будет ехать весь путь с одинаковой скоростью, то часто речь идет о средней скорости движения. Скорость машины может меняться каждую секунду, но это не помешает машине преодолеть 100 километров за 1 час.
Движение с ускорением
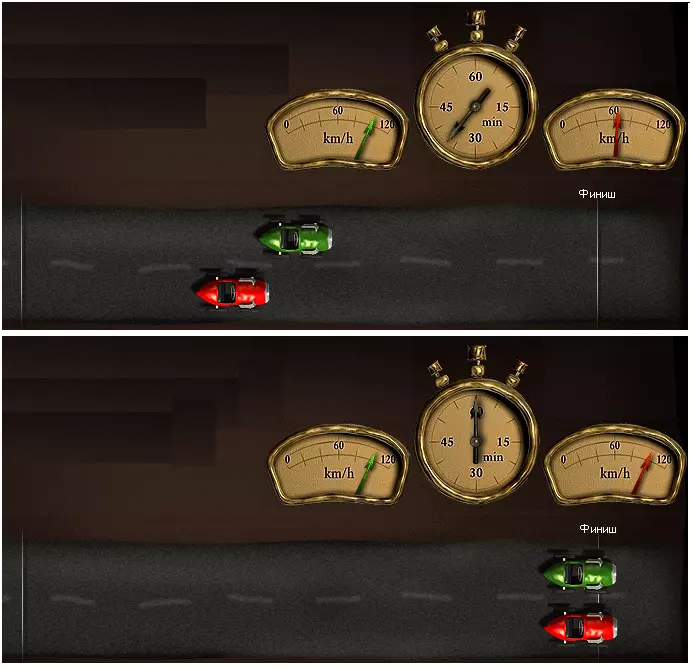
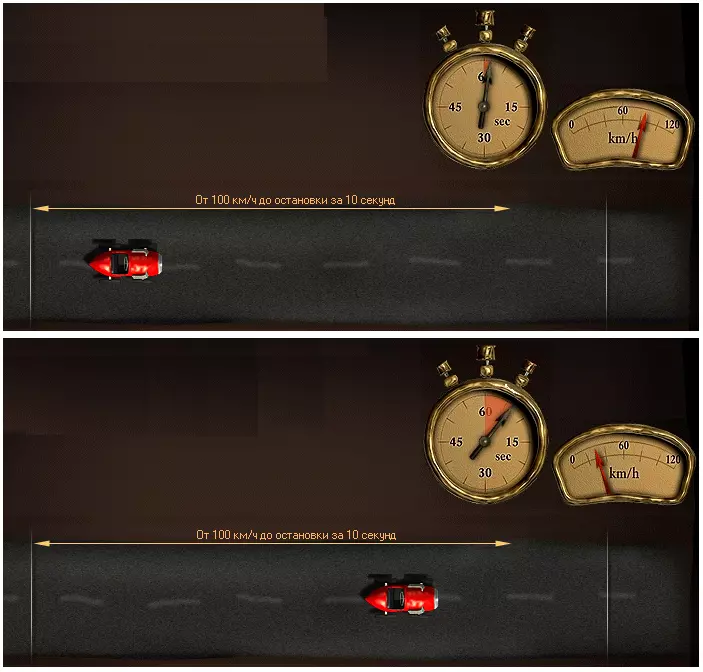
При равноускоренном движении, то есть при постоянном ускорении, машина за равные отрезки времени будет проходить все большее расстояние. Если мы рассмотрим такое движение, то моментальная скорость Vм в конце пути будет в два раза больше, чем средняя скорость Vср. В любом случае среднюю скорость тела можно вычислить таким образом: скорость тела в начале пути, обозначенная как V0, плюс моментальная скорость в конце пути Vм, деленная на 2.
Машина, которая только начинает движение и набирает желаемую скорость 100 км/ч или 27,8 м/с за 10 секунд, имеет постоянное ускорение 2,78 м/с2. Ускорение тела показывает, как быстро машина набирает определенную скорость, и обозначается a.
Если машина в течение 5 секунд после начала пути развила скорость от 0 до 100 км/ч, то ее ускорение было в два раза больше, чем в предыдущем примере.
Если машина в начале пути находилась в состоянии покоя, то, зная ускорение, можно вычислить путь, который она пройдет за определенное время. Обратимся к известным нам формулам: S = Vср * t, где Vср = Vм/2, а моментальная скорость измеряется следующим образом: Vм = a * t. Отсюда мы можем вывести формулу для пройденного пути: s = (a * t2) / 2.
При торможении движение машины замедляется, что означает движение с отрицательным ускорением.
Сила и ускорение
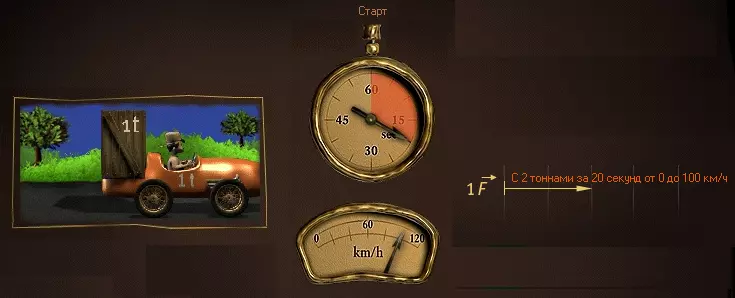
Если мы хотим, чтобы машина массой 1 тонна за 10 секунд развила скорость от нуля до 100 км/ч, то необходимо приложить силу F.
Если машина массой 2 тонны будет набирать скорость 100 км/ч за 20 секунд, то понадобится сила 1F.
Если машина массой 1 тонна разгонится от 0 до 100 км/ч, но уже за 5 секунд, то есть в два раза быстрее, то для этого понадобится приложить силу, равную 2F. При постоянной массе m сила F будет пропорциональна ускорению a: m = F/a.
Если необходимо сохранить прежнее ускорение машины, а масса составляет уже 2 тонны, то в этом случае к машине нужно приложить силу в 2F. Отсюда следует, что при постоянном ускорении сила пропорциональна массе тела: a = F/m (чем больше масса, тем больше силы надо приложить).
Отсюда следует вывод, который лег в основу закона Ньютона: F = m * a. Таким образом, сила F – это произведение массы тела m на его ускорение a.
Свободное падение
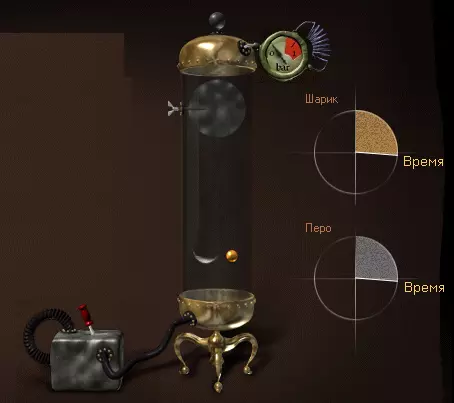
К большому удивлению своих современников Галилео Галилей утверждал, что тяжелые и легкие тела падают на Землю с одинаковой скоростью. Когда тело находится в состоянии свободного падения, то в качестве тормозящей силы будет выступать сопротивление воздуха, поэтому тела различной формы и веса будут падать с разной скоростью. Доказательством этого, может служить пример, когда мы поместим тело в вакуум, где сила сопротивления воздуха будет «выключена». Ты можешь убедиться в этом сам!
При свободном падении речь идет о равномерно ускоренном движении, которое возникает посредством действия силы гравитации Земли. Сила гравитации влияет на то, что в безвоздушном пространстве все тела за одинаковое время достигают одинаковой скорости. Ускорение при свободном падении можно вывести из формулы равномерного ускоренного движения. Исходя из того, что
Движение по окружности
Линейную скорость тела, которое двигается по окружности, в принципе можно вычислить таким же образом, как и скорость прямолинейно двигающегося тела.
Линейная скорость вращения — это отношение расстояния S, в данном случае длины окружности, и времени, затраченного на прохождение этого пути. Таким образом, мы получаем, что
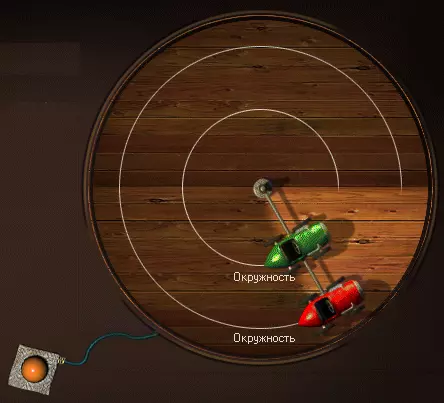
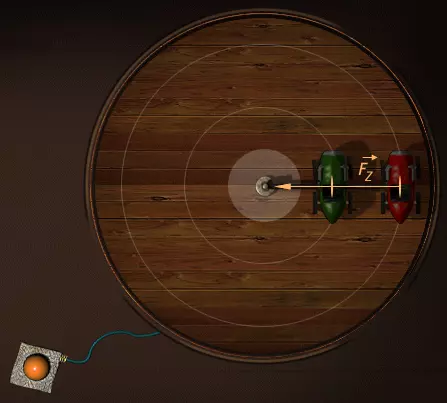
Время, затраченное двумя машинками карусели, для того чтобы сделать полный круг, будет одинаково. А вот проделанный путь у крайней машинки будет значительно больше, так как она находится на большем расстоянии от центра окружности.
Чем больше расстояние от центра окружности, тем больше должна быть линейная скорость вращения крайней машинки.
Так как внутренняя и внешняя машинка совершают полный оборот за одинаковое время, то их угловая скорость будет одинаковой. Угловой скоростью называется отношение угла поворота к интервалу времени, за который этот поворот произошел.
Сила, которая удерживает машины на треке, называется центробежной силой.
На тело действуют сила тяжести (m∙g), сила реакции опоры (N), сила трения (Ftr) (рис. ). Так как груз движется, то сила трения — это сила трения скольжения. Запишем второй закон Ньютона в векторном виде и в проекциях:
[begin{array}{c} {mcdot vec{a}=mcdot vec{g}+vec{F}_{tr} +vec{N},} \ {} \ {0X:; ; ; mcdot a=mcdot gcdot sin alpha -F_{tr} ,; ; ; (1)} \ {} \ {0Y:; ; ; 0=-mcdot gcdot cos alpha +N,; ; ; N=mcdot gcdot cos alpha ,} end{array}]
где Ftr = μ∙N. Из уравнения (1) найдем ускорение тела:
[begin{array}{c} {mcdot a=mcdot gcdot sin alpha -mu cdot mcdot gcdot cos alpha =mcdot gcdot left(sin alpha -mu cdot cos alpha right),} \ {} \ {a=gcdot left(sin alpha -mu cdot cos alpha right).; ; ; (2)} end{array}]
Скорость тела в конце спуска найдем из уравнения кинематики:
[Delta r_{x} =frac{upsilon _{x}^{2} -upsilon _{0x}^{2} }{2a_{x} } =frac{upsilon ^{2} }{2a} ,; ; ; Delta r_{x} =frac{h}{sin alpha } ,]
так как υ0 = 0 (тело начинает соскальзывать). С учетом уравнения (2) получаем:
[upsilon =sqrt{2acdot Delta r_{x} } =sqrt{frac{2acdot h}{sin alpha } } =sqrt{frac{2gcdot left(sin alpha -mu cdot cos alpha right)cdot h}{sin alpha } } ,]
υ = 13 м/с.
Второй закон Ньютона тут на фиг не нужен, потому что все тела, независимо от их массы, на высоте трёх метров нгаз землёй движутся с одним и тем же ускорением — g. Равным 9,81 м/с². То есть это задачка чисто кинематическая, а не на динамику.
Ну и учитывая уровень самой задачки, можно не заморачиваться «разложением скорости на составляющие». Ясен пень, что направлена она по вертикали, причём совершенно по фигу, вверх или вниз, потому что даже если вверх, то потом при движении вниз ЭТУ точку тело пройдёт С ТОЙ ЖЕ скоростью. Поэтому ответ АлексаМ12, в котором приращение скорости рассматривается с точки зрения баланса энергий, по направлению мысли верный, но арифметически — с грубой ошибкой, потому что складвать скорости надо квадратично, а не «+ начальные 3 метра».
Итак, будем считать, что скорость направлена вниз (раз по фигу куда). Тогда из закона сохранения энергии имеем gH+v_о²/2 = v_к²/2 (v_о — начальная скорость, v_к — конечная), откуда v_к = корень из (2gH+v_о²). И вся любовь.
Числа подставьте сами.
Разумеется, можно это решить и без привлечения закона сохранения энергии, а через квадратное уравнение S = gt²/2+v_ot, или же збавиться от времени, вспомнив, что v_о+gt = v_к, a S = 1/2 (v_о+v_к)t.