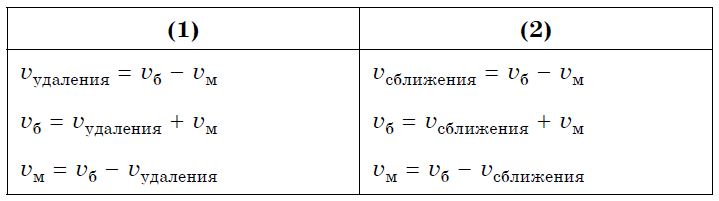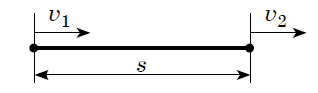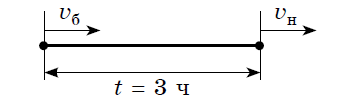Как найти скорость расстояния в одном направлении - AvtoShod.ru

Задачи на движение в одном направлении

Задачи на скорость сближения
Задача на скорость удаления

Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.

Задачи на скорость сближения

Скорость сближения — это скорость, с которой объекты сближаются друг с другом.

Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:

40 · 4 = 160 (км).

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

160 : 20 = 8 (ч).

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) — расстояние между автомобилями,

2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,

3) 160 : 20 = 8 (ч).

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

5 — 4 = 1 (км/ч).

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

5 : 1 = 5 (ч).

Решение задачи по действиям можно записать так:

1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,

2) 5 : 1 = 5 (ч).

Ответ: Через 5 часов второй пешеход догонит первого.

Задача на скорость удаления

Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.

Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.

1) Чему равна скорость удаления между автомобилями?

2) Какое расстояние будет между автомобилями через 3 часа?

3) Через сколько часов расстояние между ними будет 200 км?

Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

80 — 40 = 40 (км/ч).

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

40 · 3 = 120 (км).

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

200 : 40 = 5 (ч).

Ответ:

1) Скорость удаления между автомобилями равна 40 км/ч.

2) Через 3 часа между автомобилями будет 120 км.

3) Через 5 часов между автомобилями будет расстояние в 200 км.

Источник

Рассказываем, как решать задачи на движение в одном направлении. Приводим алгоритм решения. Задачи для самостоятельного решения.

Задачи на движение в одном направлении – задачи на нахождение скорости, времени и расстояния по заданным параметрам. при условии, что объекты двигаются в одном направлении.

Рассмотрим 2 случая:

Алгоритм решения задач на движение в одном направлении:

Записываем краткую запись;
Выбираем способ решения задачи;
Выписываем полный ответ.

В зависимости от условия задачи используются следующие формулы:

Скорость удаления (случай 1) или скорость сближения (случай 2): (V=V_б-V_м).
Расстояние, на которое объекты удаляются друг от друга (случай 1) или приближаются друг к другу (случай 2): (S=V⋅t).
Время удаления (случай 1) или сближения (случай 2): (t=S:V).

Важно помнить:

При одновременном движении объектов в одном направлении из разных пунктов:

1) расстояние между объектами постоянно, если их скорости равны;

2) расстояние между объектами уменьшается, если (V_1>V_2) (т. е. объекты сближаются);

3) расстояние между объектами увеличивается, если (V_1<V_2) (т. е. объекты удаляются).

Базовые знания:

Задача 1. В одном направлении из двух различных населенных пунктов выехали одновременно два велосипедиста. Скорость первого — 12 км/ч, а скорость второго — 14 км/ч. Найти расстояние, если второй велосипедист догонит первого через 3 ч.

Краткая запись:

Решение:

(14-12=2) (км/ч) — vудал;
(2⋅3=6) (км) — искомое расстояние.

Ответ: расстояние между населенными пунктами — 6 км.

Источник

Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.

Сейчас мы будем говорить о задачах, в которых объекты имеют разные скорости.

При движении в одном направлении объекты могут как сближаться, так и удаляться.

Здесь рассмотрим задачи на движение в одном направлении, в которых оба объекта выезжают из одного пункта. В следующий раз речь пойдет о движении вдогонку, когда объекты движутся в одном направлении из разных пунктов.

Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга.

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

$[{v_y} = {v_2} - {v_1}]$

$[({v_2} > {v_1}).]$

Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.

Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.

Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

$[{v_c} = {v_1} - {v_2}]$

$[({v_1} > {v_2}).]$

Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.

Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:

$[{v_y} = {v_2} - {v_1}]$

$[({v_2} > {v_1}).]$

Скорость, время и расстояние связаны между собой формулой пути:

Задача 1.

Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

Решение:

Условие задачи удобнее всего записать в виде таблицы:

	v, км/ч	t, ч	s, км
I велосипедист	15	4	?
II велосипедист	12	4	?

1) 15-12=3 (км/ч) скорость удаления велосипедистов

2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.

Ответ: 12 км.

Задача 2.

Из пункта А в пункт В выехал автобус. Через 2 часа вслед за ним выехал автомобиль. На каком расстоянии от пункта А автомобиль догонит автобус, если скорость автомобиля равна 80 км/ч, а скорость автобуса — 40 км/ч?

Решение:

	v, км/ч	t, ч	s, км
Автомобиль	80	?	?
Автобус	40	? на 2ч больше	?

1) 80-40=40 (км/ч) скорость сближения автомобиля и автобуса

2) 40∙2=80 (км) на таком расстоянии от пункта А находится автобус, когда автомобиль выезжает из А

3) 80:40=2 (ч) время, через которое автомобиль догонит автобус

4) 80∙2=160 (км) расстояние, которое пройдёт автомобиль от пункта А

Ответ: на расстоянии 160 км.

Задача 3

Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

Решение:

	v, км/ч	t, ч	s, км
Велосипедист	10	2	? на 12 км больше
Пешеход	?	2	?

1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода

2) 10-6=4 (км/ч) скорость пешехода.

Ответ: 4 км/ч.

Источник

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)

Примеры простых задач.

Задача 1.

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2.

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3.

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4.

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5.

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6.

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7.

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8.

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9.

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10.

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11.

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Итак, для решения задач на движение:

Основная формула:S=ν*t;
Нужно сделать чертеж, который поможет определить тип задачи.
Все цифры нужно привести в единые единицы измерения: длина и время

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

Источник

ВИДЕОУРОК

Объекты движения движутся в
одном направлении, выезжая из одного пункта одновременно.

Рассмотрим случай,
когда объекты движения могут двигаться в одном направлении, причём с различной
скоростью.

Например, из одного
пункта одновременно могут выехать велосипедист и мотоциклист, причём скорость
велосипедиста может составлять 20 км/час,
а скорость мотоциклиста – 40 км/час.

После начала
движения, через один час, мотоциклист будет впереди велосипедиста на 20 км. Это
связано с тем, что за один час он преодолевает на 20
км больше, чем велосипедист. Поэтому каждый час
расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать
километров. В данном случае 20 км/час являются скоростью удаления мотоциклиста от
велосипедиста. Через два часа расстояние, пройденное велосипедистом, будет
составлять 40
км. Мотоциклист же проедет 80
км, отдалившись от велосипедиста
ещё на 20
км. Тогда расстояние между ними
составит уже 40
км.

Чтобы найти
скорость удаления при движении в одном направлении, нужно из большей скорости
вычесть меньшую скорость.

В приведённом
примере, скорость удаления составляет 20 км/час.
Её можно найти путём вычитания скорости велосипедиста из скорости мотоциклиста.
Скорость велосипедиста составляла 20 км/час,
а скорость мотоциклиста – 40
км/час. Скорость
мотоциклиста больше, поэтому из 40 вычитаем
20.

40 км/час –
20
км/час = 20
км/час.

ЗАДАЧА:

Из города в одном и том же направлении выехали легковой
автомобиль и автобус. Скорость автомобиля
120
км/час, а скорость автобуса 80 км/час. Какое расстояние будет между ними через 1
час ? 2
часа ?

РЕШЕНИЕ:

Найдём скорость удаления. Для этого из большей скорости
вычтем меньшую скорость:

120 км/час – 80 км/час = 40 км/час.

Каждый час легковой автомобиль отдаляется от автобуса
на 40
километров. За один час расстояние между автомобилем и автобусом будет 40
км. За 2
часа в два раза больше:

40 ∙ 2 = 80 (км).

ОТВЕТ: 80 км

ЗАДАЧА:

Из одного пункта в одном направлении одновременно выехали
два мотоциклиста. Скорость одного 35 км/час,
а скорость другого составляла 80% скорости первого мотоциклиста. Какое
расстояние будет между ними через 5 часов ?

РЕШЕНИЕ:

Найдём скорость второго мотоциклиста. Она составляет 80% скорости первого
мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно
найти 80% от 35 км/час.

35 ∙ 0,80 = 28 км/час.

Первый мотоциклист двигается на 7 км/час быстрее:

35 км/час – 28
км/час = 7 км/час.

За один час первый мотоциклист преодолевает на 7 км больше. С каждым часом он будет отдаляться от
второго мотоциклиста на эти 7 км. Через 5 час первый
мотоциклист пройдёт:

35 ∙ 5 = 175 (км),

а второй:

28 ∙ 5 = 140 (км),

Определим расстояние, которое будет между ними через 5
час:

175 км – 140
км = 35 км.

ОТВЕТ: 35 км

ЗАДАЧА:

Автомобиль и автобус выехали одновременно из одного
пункта в одном направлении. Скорость автомобиля
53
км/час, скорость автобуса 41
км/час. Через сколько часов после выезда автомобиль будет впереди автобуса
на 48
км ?

РЕШЕНИЕ:

Найдём скорость удаления автомобиля от автобуса:

53 км/час – 41
км/час = 12 км/час.

С каждым часом автомобиль будет удаляться от автобуса
на 12
км. Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48
км, нужно определить сколько раз 48 км содержат
по 12
км:

48 : 12 = 4 (час).

ОТВЕТ: 4 час

ЗАДАЧА:

Из одного города одновременно в одном направлении
выехали грузовик со скоростью 48 км/год и
легковой автомобиль со скоростью 64 км/год. Каким будет расстояние между ними
через 3 часа после начала движения ?

РЕШЕНИЕ:

64 – 48 = 16 (км) – на столько километров увеличится расстояние между автомобилями каждый
час.

16 ∙ 3 = 48 (км) –
расстояние между автомобилями через 3 час.

ОТВЕТ: 48
км

ЗАДАЧА:

Из города Минск в Смоленск, расстояние между
которыми 346
км, отправились одновременно велосипедист и автомобилист. Скорость
автомобиля 20 м/сек, а велосипедиста
20 км/час.
Какое расстояние будет между ними через 2 часа ?

РЕШЕНИЕ:

Нельзя складывать разные единицы измерения, поэтому надо
перевести метры в секунду в километры в час. Так как в

1 километре – 1000 метров, а в

1 часе – 3600 секунд, тогда

1 км/час = 1000 : 3600 = ⁵/₁₈ м/сек.

Составим пропорцию:

1 км/час ———— ⁵/₁₈ м/сек,

х км/час ———— 20 м/сек,

Скорость автомобиля – 72 км/час.

Так как автомобилист и
велосипедист выехали из одного места и двигаются в одном направлении,
расстояние между ними за один час будет нарастать со скоростью:

72 – 20 = 52 (км/час).

А через 2 часа оно будет равно:

52 ∙ 2 = 104 (км).

ОТВЕТ: 104
км

Объекты движения движутся в
одном направлении, выезжая из разных пунктов одновременно.

Рассмотрим
ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном
направлении.

Пусть имеется дом,
школа и аттракцион. От дома до школы 700 м.
Два пешехода отправились в аттракцион в одно и то же время. Причём первый
пешеход отправился в аттракцион от дома со скоростью 100 м/мин, а второй пешеход отправился в аттракцион от школы со
скоростью 80 м/мин. Какое расстояние будет между пешеходами через 2 минуты ? Через сколько минут после начала движения
первый пешеход догонит второго ?

Ответим на первый
вопрос задачи – какое расстояние будет между пешеходами через две минуты ?

Определим
расстояние, пройденное первым пешеходом за
2
мин. Он двигался со
скоростью 100 м/мин. За две минуты он пройдёт в два раза больше, то
есть 200 м.

100 ∙ 2 = 200 (м).

Определим
расстояние, пройденное вторым пешеходом за
2
мин. Он двигался со
скоростью 80 м/мин. За две минуты он пройдёт в два раза больше, то
есть 160 м.

80 ∙ 2 = 160 (м).

Теперь нужно найти
расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к
расстоянию от дома до школы (700 м) прибавить расстояние, пройденное вторым пешеходом (160 м)
и из полученного результата вычесть расстояние, пройденное первым пешеходом (200 м).

700 м + 160 м = 860 м,

860 м – 200 м = 660 м.

Либо из расстояния
от дома до школы (700 м) вычесть расстояние, пройденное первым пешеходом (200 м),
и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160 м).

700 м – 200 м = 500 м,

500 м + 160 м = 660 м.

Таким образом,
через две минуты расстояние между пешеходами будет составлять 660 м.

Ответим на
следующий вопрос задачи. Через сколько минут после начала движения первый
пешеход догонит второго ? Посмотрим
какой была ситуация в самом начале пути – когда пешеходы ещё не начали
движение. Расстояние между пешеходами в начале пути составляло 700 м. Но уже через минуту после начала движения расстояние
между ними будет составлять 680 м,
поскольку первый пешеход двигается на 20 м быстрее второго:

100 м ∙ 1 = 100 м,

80 м ∙ 1 = 80 м,

700 м + 80 м – 100 м =

= 780 м – 100 м = 680 м.

Через две минуты
после начала движения, расстояние уменьшится ещё на 20 м и будет
составлять 660 м.

100 м ∙ 2 = 200 м,

80 м ∙ 2 = 160 м,

700 м + 160 м – 200 м =

= 860 м – 200 м = 660 м.

Через три минуты
расстояние уменьшится ещё на 20 м и будет уже составлять 640 м.

100 м ∙ 3 = 300 м,

80 м ∙ 3 = 240 м,

700 м + 240 м – 300 м =

= 940 м – 300 м = 640 м.

Мы видим, что с
каждой минутой первый пешеход будет приближаться ко второму на 20 м, и, в конце концов, догонит его. Можно сказать, что
скорость равная двадцати метрам в минуту является скоростью сближения
пешеходов. Правила нахождения скорости сближения и удаления при движении в
одном направлении идентичны.

Чтобы найти
скорость сближения при движении в одном направлении, нужно из большей скорости
вычесть меньшую скорость.

А раз
изначальные 700 м с каждой минутой
уменьшаются на одинаковые 20 м,
то можно узнать сколько раз 700 м содержат по
20 м, тем самым определим, через сколько минут первый пешеход
догонит второго:

700 : 20 = 35.

Значит, через 35
мин после начала движения первый пешеход догонит
второго. Узнаем, сколько метров прошёл к этому времени каждый пешеход.

Первый двигался со
скоростью 100 м/мин. За 35 мин он прошёл в
35 раз больше:

100 м ∙ 35 = 3500 м.

Второй двигался со
скоростью 80 м/мин. За 35 мин он прошёл в
35 раз больше:

80 м ∙ 35 = 2800 м.

Первый прошёл 3500 м, а второй 2800 м.
Первый прошёл на 700 м больше, поскольку он шёл от дома. Если
вычесть эти 700
м из 3500 м,
то мы получим 2800 м.

ЗАДАЧА:

Из двух сёл, расстояние между которыми 40
км, одновременно в одном направлении выехали автобус и велосипедист. Скорость
велосипедиста 15 км/час, а скорость автобуса 35 км/час.
Через сколько часов автобус догонит велосипедиста ?

РЕШЕНИЕ:

Найдём скорость сближения:

35 км/час – 15 км/час = 20 км/час.

Определим, через сколько часов автобус догонит
велосипедиста:

40 : 20 = 2 (час).

ОТВЕТ: 2 час

ЗАДАЧА:

Расстояние между двумя посёлками равно 24
км. Из этих посёлков одновременно в одном направлении вышли пешеход, и выехал
велосипедист. Впереди шёл пешеход. Через сколько часов после начала движения
велосипедист догонит пешехода, если пешеход шёл со скоростью 4
км/час, а велосипедист ехал со скоростью
12
км/час ?

РЕШЕНИЕ:

12 – 4 = 8 (км) – на столько уменьшилось расстояние между велосипедистом и пешеходом за
один час.

24 : 8 = 3 (час) – время, за которое
велосипедист догнал пешехода.

ОТВЕТ: 3
год

Объекты движения движутся в
одном направлении, но один из объектов начал своё движение раньше другого.

Рассмотрим
ситуацию, в которой объекты движутся в одном направлении, но один из объектов
начал своё движение раньше другого.

Пусть имеется дом и
школа. Первый пешеход отправился в школу со скоростью 80 м/мин. Через 5 мин вслед за ним в школу отправился второй
пешеход со скоростью 100 м/мин.
Через сколько минут второй пешеход догонит первого ?

Второй пешеход
начал своё движение через 5 мин.
К этому времени первый пешеход уже отдалился от него на какое-то расстояние.
Найдём это расстояние. Для этого умножим его скорость (80 м/мин)
на 5
мин.

80 ∙ 5 = 400 (м).

Первый пешеход
отдалился от второго на 400 м.
Поэтому в момент, когда второй пешеход начнёт своё движение, между ними будут
эти самые 400 м. Но второй пешеход двигается со скоростью 100 м/мин. То есть двигается на
20 м быстрее первого
пешехода, а значит с каждой минутой расстояние между ними будет уменьшаться
на 20 м. Надо узнать через сколько минут второй пешеход догонит
первого. Например, уже через минуту расстояние между пешеходами будет
составлять 380 м. Первый пешеход к своим
400 м пройдёт ещё 80 м, а второй
пройдёт 100 м. Расстояние между пешеходами в момент движения второго
пешехода необходимо разделить на скорость сближения пешеходов. Скорость
сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить
через сколько минут второй пешеход догонит первого, нужно 400 м разделить на 20.

400 : 20 = 20 (мин).

Значит, через 20
мин второй пешеход догонит первого.

ЗАДАЧА:

Легковая машина, скорость которой 62 км/час,
догоняет грузовую машину, скорость которой
47 км/час.
Через сколько времени и на каком расстоянии от начала движения легковая машина
догонит грузовую, если первоначальное расстояние между ними было 60
км ?

РЕШЕНИЕ:

Найдём скорость сближения:

62 км/час – 47 км/час = 15 км/час.

Если первоначально расстояние между машинами было 60
км, то с каждым часом это расстояние будет уменьшаться на 15
км, и в конце концов легковая машина догонит грузовую. Чтобы узнать, через
сколько часов это произойдёт, нужно определить сколько раз 60
км содержит
по 25
км.

60 : 15 = 4 (час).

Узнаем, на каком расстоянии от начала движения, легковая
машина догнала грузовую машину. Для этого умножим скорость легковой машины на
время её движения до встречи.

62 ∙ 4 = 248 (км)

ОТВЕТ: 4 час, 248 км

ЗАДАЧА:

Мотоциклист, скорость которого 43 км/час, догоняет велосипедиста, скорость которого 13 км/час. Через сколько часов мотоциклист догонит
велосипедиста, если первоначальное расстояние между ними было 120
км ?

РЕШЕНИЕ:

Найдём скорость сближения:

43 км/час – 13 км/час = 30 км/час.

Если первоначальное расстояние между мотоциклистом и
велосипедистом было 120 км, то с каждым часом это расстояние будет уменьшаться
на 30
км, и, в конце концов, мотоциклист догонит велосипедиста. Чтобы узнать, через
сколько часов это произойдёт, нужно определить сколько раз 120
км содержит по 30
км:

120 : 30 = 4 (час).

Значит, через 4 часа мотоциклист
догонит велосипедиста.

ОТВЕТ: 4 час

ЗАДАЧА:

Велосипедист, скорость которого 12 км/час, догоняет велосипедиста, скорость которого
составляет 75% от его скорости. Через 6
час второй велосипедист догнал
велосипедиста, ехавшего первым. Какое расстояние было между ними первоначально ?

РЕШЕНИЕ:

Определим скорость велосипедиста, ехавшего впереди. Для
этого найдём 75% от скорости велосипедиста, ехавшего сзади:

612 ∙ 0,75 = 9 (км/час).

Узнаем, сколько километров проехал каждый велосипедист до
того как второй догнал первого:

12 ∙ 6 = 72 (км),

9 ∙ 6 = 54 (км).

Узнаем, какое расстояние было между ними первоначально.
Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым
велосипедистом (которого догоняли).

72 км – 54 км = 18 км.

ОТВЕТ: 18 км

ЗАДАЧА:

Из пункта А выехал велосипедист и едет по направлению
пункта В со средней скоростью 12
км/час. Через 2
час из этого же пункта отправился в том
же направлении второй велосипедист со скоростью
18 км/час. Через сколько часов и на каком расстоянии
от А второй велосипедист догонит первого ?

РЕШЕНИЕ:

Определим, какое расстояние проходит первый велосипедист
до выезда второго:

12 × 2 = 24 (км).

Определим, на сколько километров больше проходит в час
второй велосипедист, чем первый:

18 – 12 = 6 (км).

Найдём через сколько часов после своего выезда второй
велосипедист догонит первого:

24 км : 6 км = 4 (час),

а теперь определим, на каком расстоянии от А второй велосипедист догонит первого:

18 × 4 = 72 (км).

ОТВЕТ:

4
час, 72 км.

ЗАДАЧА:

Первый турист проехал
2
часа на велосипеде со скоростью 16
км/час. Отдохнув 2 часа, он отправился дальше с прежней скоростью.
Спустя 4
часа после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле
со скоростью 56 км/час. На каком расстоянии от места старта мотоциклист
догонит велосипедиста ?

РЕШЕНИЕ:

Пусть туристы отправились из точки А.
Тогда В –
место стоянки велосипедиста, далее за точкой
В точка С – место, в котором мотоциклист догнал велосипедиста (точки А,
В и С находятся на одной прямой). Пусть АС = S.
Велосипедист проехал это расстояние за ^s/₁₆
час, а мотоциклист – за ^s/₅₆
час. Тогда из условия задачи:

^s/₁₆ – ^s/₅₆ = 2.

Откуда S = 44,8 км

ОТВЕТ: 44,8 км

Задания к уроку 20

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Отношение величин

Урок 2. Пропорции

Урок 3. Величины прямо пропорциональные

Урок 4. Величины обратно пропорциональные

Урок 5. Пропорциональное деление

Урок 6. Проценты

Урок 7. Нахождение процентов данного числа (задачи)

Урок 8. Нахождение числа по его процентам (задачи)

Урок 9. Нахождение процентного отношения двух чисел (задачи)

Урок 10. Простые и сложные проценты

Урок 11. Задачи на время

Урок 12. Задачи на нахождение чисел по их сумме или разности

Урок 13. Задачи на нахождение чисел по их сумме или разности и отношению

Урок 14. Среднее арифметическое

Урок 15. Среднее арифметическое (задачи)

Урок 16. Масштаб карты или чертежа

Урок 17. Определение расстояния на местности и действительных размеров предметов с помощью масштаба

Урок 18. Определение расстояния на карте или чертеже с помощью масштаба

Урок 19. Задачи на встречное движение

Урок 21. Задачи на движение в противоположных направлениях

Урок 22. Задачи на движение по реке

Урок 23. Задачи на совместную работу

Источник

Задачи на движение в одном направлении

Задачи на скорость сближения

Задача на скорость удаления

Базовые знания:

Скорость, время и расстояние: определения, обозначения, формулы

Задача 1.

Задача 2.

Задача 3.

Задачи на встречное движение

Задача 4.

Задача 5.

Задачи на движение в противоположных направлениях

Задача 6.

Задача 7.

Задачи на движение в одном направлении

Задача 8.

Задача 9.

Задача 10.

Задачи на движение по реке

Задача 11.

Итак, для решения задач на движение:

Заключение.

ВИДЕОУРОК

Не пропустите также: