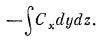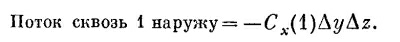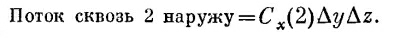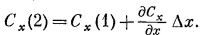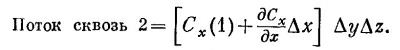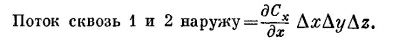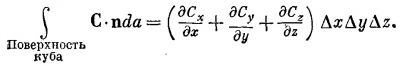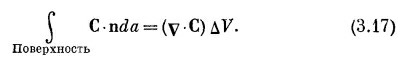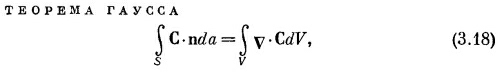Подсказка: 1) Расставим силы действующие на куб и груз. На куб, в направлении движения, действует сила натяжения нити. А на груз, кроме силы тяжести, действует сила упругости нити (натяжения нити). По второму закону Ньютона — результирующая сила сообщает телам ускорение.
2) Груз находится на высоте H, это позволит нам определить время его движения (зная ускорение), столько же времени (до удара) движется и куб.
3) И последнее, если куб сместится по горизонтали на некоторое расстояние, то груз сместится на то же расстояние вниз, следовательно, горизонтальное ускорение куба равно вертикальному ускорению груза.
Успехов в решении задачи. Опубликуйте решение.
Как вычислить скорость падения куба в воздухе и в воде?
Пишу 2D игру. Возник вопрос. Есть куб. Известен его объем и плотность. Как рассчитать с какой скоростью (можно приблизительную) этот куб будет падать в воде и воздухе? Гугл ничего толкового не говорит, у самого идей тоже нет.
-
Вопрос задан12 июн. 2022
-
192 просмотра
Для игры достаточно:
на падающий объект действуют силы — вектор приложенной (текущей) скорости, ускорения свободного падения, трения о среду и архимедова сила (для воды)
пока объект в воде в формулу расчета следующего тика скорости (или куда ты там вектор воздействия пишешь) добавляй вектор архимедовой силы вверх (забей константу для воды, для игры хватит) и можно добавить еще тормозящий вектор в противоположную сторону оттекущего движения — сопротивление среды.
Пригласить эксперта
Нужно ограничить скорость падения куба в воздухе. Как парашютиста в свободном падении.
Кроме того при вхождении куба в воду на такой скорости я-бы рассмотрел не только Архимедову силу. Мне кажется тут еще должны быть какие-то модели. Вода — несжимаемая. Тут либо куб должен деформироваться либо вода.
-
Показать ещё
Загружается…
26 мая 2023, в 12:40
2000 руб./за проект
26 мая 2023, в 12:15
30000 руб./за проект
26 мая 2023, в 12:15
6000 руб./за проект
Минуточку внимания
2018-11-09
На абсолютно гладкой горизонтальной плоскости лежит куб, опираясь на плоскость одним из ребер. Угол между гранью куба и горизонтальной плоскостью составляет $45^{ circ}$. Такое положение куба явно неустойчиво, и от самого слабого толчка куб переворачивается. Найти угловую скорость куба в момент» когда его боковая грань ударяется о горизонтальную плоскость. Ребро куба равно $a$, масса — $m$.
Решение:
На куб действуют следующие внешние силы: сила тяжести и сила реакции опоры, обе направленные по вертикали. В горизонтальном направлении па куб не действуют никакие силы, а значит, горизонтальная составляющая импульса центра куба должна быть постоянной во времени. Поскольку эта составляющая в начальный момент была равна нулю, она остается равной нулю все время. Это означает, что центр куба будет перемещаться только в вертикальном направлении. Искомую угловую скорость $omega$ определим из условия
$frac{1}{2}mv^{2} + frac{1}{2} I omega (конечная, кинетическая quad энергия quad (начальнаяquad былаquad равна quadнулю)) = mg frac{a}{2} ( sqrt{2} — 1) (разность quad начальной quad и конечной quad потенциальной quad энергии) $, (1)
где $v$ — скорость центра масс куба, $I$ — момент инерции куба относительно оси, проходящей через центры противоположных граней, $omega$ — угловая скорость к>ба относительно той же оси в конечный момент.
Чтобы определить угловую скорость $omega$, следует сначала установить зависимость между $v$ и $omega$ в конечный момент и найти соответствующее выражение для $I$.
Линейная скорость ребра, скользящего по горизонтальной поверхности, в системе отсчета, которая движется вертикально вместе с центром куба, равна произведению $omega$ на половину диагонали квадрата, являющегося боковой гранью куба:
$v_{1} = omega frac{1}{2} a sqrt{2}$.
В конечный момент скорость $v_{1}$ направлена под углом $45^{ circ}$ к горизонтали. Вертикальная составляющая $v^{ prime}$ скорости $v$ равна при этом
$v^{ prime} = frac{1}{2} sqrt{2} v_{1} = frac{1}{2} omega a$.
Очевидно, такое же значение имеет скорость $v$:
$v = frac{1}{2} omega a$.
Определим теперь момент инерции $I$. Ясно, что момент инерции куба относительно оси, проходящей через центры противоположных граней, равен по величине моменту инерции тонкой квадратной пластины (масса которой равна массе куба и сторона равна ребру куба) относительно оси, перпендикулярной к плоскости пластины и проходящей через ее середину.
Мысленно поделим пластину на очень малые элементы массой $m_{i}$. Согласно рис., имеем
$I = sum_{i} m_{i}r_{i}^{2} = sum_{i} m_{i} (x_{i}^{2} + y_{i}^{2} ) = sum_{i} m_{i}x_{i}^{2} + sum_{i} m_{i}y_{i}^{2}$.
Из соображений симметрии
$sum_{i} m_{i}x_{i}^{2} = sum_{i} m_{i}y_{i}^{2}$. Значит, $I = 2 sum_{i} m_{i}x_{i}^{2}$.
Отметим, что $sum_{i} m_{i}x_{i}^{2}$ означает момент инерции пластины относительно оси, совпадающей с осью у. Этот момент, очевидно, равен моменту инерции стержня (масса которого равна массе пластины, а длина равна ее стороне) относительно оси, проходящей через центр стержня и перпендикулярной к нему. Момент инерции стержня равен $ma^{2}/12$, поэтому
$I = 2 frac{1}{12} ma^{2} = frac{1}{6} ma^{2}$,
Это равенство можно получить также на основании теоремы Штейнера и анализа размерностей. Момент инерции тела равен
$I = sum_{i} m_{i}r_{i}^{2}$.
Если массу каждого элемента увеличим в $k$ раз, то момент увеличится в $k$ раз. Следовательно, можно записать $I sim m$.
Аналогично если размер каждого элемента $r_{i}$ увеличить в $l$ раз, то момент инерции $I$ возрастет в $l^{2}$ раз, а все линейные размеры пластины увеличатся пропорционально $l$. Значит, $I sim a^{2}$.
Обобщая эти две зависимости, получим
$I sim alpha ma^{2}$. (2)
Величина $ma^{2}$ имеет размерность момента инерции, поэтому коэффициент пропорциональности $alpha$ должен быть безразмерным, ибо единственными параметрами, характеризующими механические свойства пластины, являются $m$ и $a$.
Поделим теперь пластину на четыре части, как показано на рис. Момент инерции каждой из четырех частей относительно оси, проходящей через точку О и перпендикулярной к плоскости рисунка, обозначим через $I_{1}$. Тогда
$I = 4I_{1}$, но по теореме Штейнера $I_{1} = I^{ prime} + frac{m}{4} d^{2}$,
где $I^{ prime}$ — момент инерции каждой из четырех частей относительно собственного центра. Согласно уравнению (2),
$I^{ prime} = alpha frac{m}{4} left ( frac{a}{2} right )^{2}$,
откуда
$alpha ma^{2} = 4 left [ alpha frac{m}{4} left ( frac{a}{2} right )^{2} + frac{m}{4} left ( frac{ sqrt{2} }{4} right )^{2} a^{2} right ]$.
Тогда $alpha = 1/6$, а2
$I = frac{1}{6} ma^{2}$.
Подставляя в уравнение (1) зависимость $v$ от $omega$, а также полученное выражение для $I$, найдем
$omega = sqrt{ frac{12g}{5a} ( sqrt{2} — 1 )}$.
Кубы (кубики) – это сленговое название единиц измерения рабочего объема мотора мотоцикла. Один кубик подразумевает один кубический сантиметр рабочего объема двигателя.
Какая скорость на 125 кубов?
Максимальная скорость Модели с мотором объемом 125 -140 см³ в среднем развивают максимальную скорость до 100 км/ч. Питбайки со 190- кубовым мотором быстрее – могут разогнаться до 120 км/ч. Мотоцикл. «Малокубатурники» с двигателем объемом 125 -150 см³ развивают скорость 100-120 км/ч.
Какая максимальная скорость у 400 кубового мотоцикла?
Максимальная скорость равняется всего 135 км/ч, поэтому данный мотоцикл подходит для спокойной, но уверенной езды. Коробка передач механическая пятиступенчатая, привод на заднее колесо выполнен через карданный вал.
Что значит Кубы?
Куба (исп. Cuba) — островное государство в Карибском море. Куба (исп. Cuba) — крупнейший остров Республики Куба.
Какая максимальная скорость у 250 кубового мотоцикла?
Максимальная скорость составляет 140 км/час.
Чем отличается 125 кубов от 140?
Собственно разница по двигателям такая: 125 — низовой трактор, 140 — ровный середнячок, 150(160) — верховой двигатель. Все логично, так как кубатура изменяется диаметром поршня, вот и получается, что у 160 кубов практически поршень равен ходу, а это максимальная мощь, а не тяга.
Какая скорость у 150 кубов?
Тогда вам идеально подойдет среднеразмерный мотороллер. Максимальная скорость 150 -кубовых скутеров составляет 85-130 км/ч, а их грузоподъемность достигает 140-160 кг.
Сколько едет мотоцикл 600 кубов?
Разгон до 100 км занимает 3 секунды, а максимальная скорость составляет 260 км/час.
Сколько едет мотоцикл 1000 кубов?
Разгон до 100 км/ч происходит за 3,1 с. Максимальная скорость мотоцикла 299 км/ч.
Сколько лошадиных сил в 1000 кубов?
Двигатель
| Тип | Четырехцилиндровый четырехтактный рядный двигатель с масляно-водяным охлаждением, четыре клапана на цилиндр |
|---|---|
| Рабочий объем | 999 куб. см |
| Максимальная мощность | 121 кВт (165 л.с.) при 11000 об/мин |
| Максимальный крутящий момент | 114 Нм при 9250 об/мин |
| Степень сжатия | 12,5 : 1 |
Какой расход у 200 кубового мотоцикла?
Максимальная скорость мотоцикла 100 км/час при этом расход топлива составляет 2,4 л/100 км.
Сколько стоит мотоцикл 250 кубов?
GR2 250 Enduro LITE 21/18 (2020 г.) 185 990 руб. GR2 250 Enduro OPTIMUM 21/18 (2020 г.) 200 990 руб.
Сколько ест мотоцикл на 100 км?
Расход топлива Средний мотоцикл расходует 5—7 л топлива на 100 км. Расход изменяется в зависимости от скорости, характера дороги и стиля вождения.
Какой самый мощный мотоцикл?
Ну а из крупносерийных самый мощный мотоцикл – это, конечно же, Suzuki Hayabusa GSX1300R. Его 197 л.с. может и не так удивляют, как у двух предыдущих моделей, но этого достаточно, чтобы развить скорость до 330 км/ч.
Что дает объем двигателя на мотоцикле?
Чем больше объем одного цилиндра, тем больше обычно момент, а двигатель более заточен под тяговую езду. И наоборот, чем меньше объем одного цилиндра, тем меньше обычно крутящий момент, а двигатель более оборотистый.
Какой 600 кубовый мотоцикл лучше купить?
Дорожные байки на 600 кубов В этом случае стоит взглянуть на «классику» и 600 кубовые мотоциклы могут здесь предложить следующий выбор: Honda CBF600, а если конкретнее, то простой CB600FA и подвид «Hornet». Это достаточно сильно модифицированное и улучшенное поколение хорошо знакомой всем байкерам 90-ых «си-бихи».
Какая максимальная скорость у 110 кубов?
Объем: 110 куб. см. Макс. скорость 50 км/ч.
Сколько едет питбайк 150 кубов?
Разгоняется пит при весе 83 кг до 90 км/ч. Расход топлива по грунтовым дорогам – примерно 3 л/100 км.
Сколько сил у 125 кубов?
Техническая характеристика модели К-125М
| Длина, мм | 1 950 |
|---|---|
| Рабочий объём двигателя, см³ | 123 |
| Степень сжатия | 6,5 |
| Мощность двигателя, л.с. | 4,25 |
| Обороты при макс. мощности об/мин | 4 800 |
Какая максимальная скорость у 200 кубового мотоцикла?
Сравнительная таблица характеристик разных мотоциклов
| Класс (объем двигателя, куб.см.) | 125-150 | 200 -250 |
|---|---|---|
| На примере модели | BAJAJ Pulsar 150 | BAJAJ Pulsar 200NS |
| Мощность, л.с. | 15 | 24 |
| Максимальная скорость, км/ч | 125 | 155 |
Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 3. Интегральное исчисление векторов
Поток из куба; теорема Гаусса
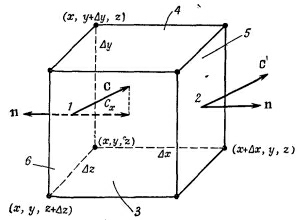
Так как куб считается малым, этот интеграл можно заменить значением Сх в центре грани [эту точку мы обозначили (1)], умноженным на площадь грани ΔyΔz:
Подобным же образом поток наружу через грань 2 равен
Величины Сх(1) и Сх(2), вообще говоря, слегка отличаются. Если Δx достаточно мало, то можно написать
Существуют, конечно, и другие члены, но в них входит (Δx)2 и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
Складывая потоки через грани 1 и 2, получаем
Производную нужно вычислять в центре грани 1, т. е. в точке [х, y + (Δy/2), z+(Δz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).
Повторяя те же рассуждения с каждой парой граней, мы получаем
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
Сумма производных в скобках как раз есть v·С, a ΔxΔyΔz=ΔV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р.
Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.
где S — произвольная замкнутая поверхность, V — объем внутри нее.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle