Фотоэффект. Законы Столетова. Формула Эйнштейна
Изучение закономерностей теплового излучения привело к чрезвычайно важному выводу о существовании квантов энергии, о дискретном характере электромагнитного излучения. Гипотезу о квантах излучаемой энергии М. Планк выдвинул в 1900 г. Несколько позже А. Эйнштейн выдвинул гипотезу о том, что свет не только излучается, но и распространяется в пространстве и поглощается также в виде квантов дискретного электромагнитного излучения. Кванты видимого излучения получили название фотонов.
К физическим явлениям, подтверждающим квантовую природу излучения, относится фотоэффект. Фотоэффект – это явление вырывания электронов из атомов и молекул вещества под действием света (электромагнитного излучения). Если выбитые электроны вылетают за пределы вещества, то фотоэффект называется внешним и наблюдается, главным образом, у металлов. Если же оторванные от своих атомов и молекул электроны остаются внутри освещаемого вещества в качестве свободных электронов, то фотоэффект называется внутренним. Он наблюдается у некоторых полупроводников и, в меньшей степени, диэлектриков. Это явление обнаружено Герцем в 1887 г., изучено Столетовым в 1888-89 г.г., т.е. до появления гипотезы Планка. Герц обнаружил, а Столетов изучил и установил, что
испускаемые заряды имеют отрицательный знак;
наибольшее действие на выход электронов оказывают ультрафиолетовые лучи — величина испущенного заряда пропорциональна поглощенной телом энергии.
Схема опытов Столетова по исследованию внешнего фотоэффекта изображена на рис. 162. В вакуумной трубке помещают исследуемую пластинку К (катод) и вспомогательный электрод А (анод).
Электроды А и К через потенциометр П подключены к источнику напряжения Е. Напряжение между электродами, называемое анодным, измеряется вольтметром V, а ток в цепи гальванометром Г. Если пластинка К не освещается, то ток в цепи отсутствует, т.к. вакуумный промежуток между катодом и анодом тока не проводит. Если же исследуемую пластинку осветить светом через окно С, то свет вырвет из пластинки электроны, которые получили название фотоэлектронов. Под действием электрического поля, созданного анодным напряжением, фотоэлектроны будут двигаться к аноду А и далее по замкнутой цепи через гальванометр Г к катоду К. Гальванометр покажет наличие тока, который получил название фототока. При помощи потенциометра П можно изменять величину и знак анодного напряжения. Следует иметь в виду, что ток в цепи существует и в том случае, когда анодное напряжение равно нулю, и даже при небольшом отрицательном (задерживающем) напряжении. Объясняется это тем, что вылетевшие из катода фотоэлектроны обладают кинетической энергией, за счет которой совершается работа против сил поля и они достигают анода. На графике на рис. 161 показана типичная зависимость силы фототока от анодного напряжения (т.н. вольт-амперная характеристика) при неизменном световом потоке для двух значений светового потока Ф, когда Ф1 < Ф2. Из графика видно, что:
При некотором небольшом напряжении фототок достигает насыщения – все электроны попадают на анод;
При U = 0 фототок не исчезает, значит электроны покидают катод со скоростью, отличной от нуля;
Для того, чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение Uз.
Измерив Uз, можно определить максимальную скорость фотоэлектронов, покидающих катод

Исследования Столетова привели к установлению 3-х основных законов фотоэффекта:
Сила фототока насыщения Iн прямо пропорциональна падающему световому потоку Ф
где к – коэффициент пропорциональности.
Скорость фотоэлектронов увеличивается с увеличением частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока
Независимо от интенсивности светового потока фотоэффект начинается при определенной для данного вещества минимальной частоте (максимальной длине) световой волны, называемой красной границей фотоэффекта.
2-й и 3-й законы фотоэффекта противоречат представлениям волновой теории света. Согласно этим представлениям электроны вещества должны совершать колебания с амплитудой, пропорциональной амплитуде падающей световой волны. При достаточной амплитуде связь электрона с веществом может быть нарушена и электроны будут вылетать наружу со скоростью, величина которой будет зависеть от амплитуды, т.е. интенсивности падающего света. В действительности такой зависимости нет, скорость электронов зависит только от частоты падающего света.
Для объяснения этого факта Эйнштейн выдвинул гипотезу, что свет не только испускается, но и распространяется и поглощается дискретными порциями – квантами. По Эйнштейну квант энергии (света) поглощается полностью одним электроном и энергия кванта hν расходуется на работу по вырыванию электрона из вещества Авых и на сообщение электрону кинетической энергии
hν = Авых+
Эта формула получила название формулы Эйнштейна для фотоэффекта.
Работа выхода зависит от рода вещества, состояния и чистоты поверхности и других факторов, экспериментально определена и для некоторых веществ приводится в справочниках. Из формулы Эйнштейна вытекает второй закон фотоэффекта
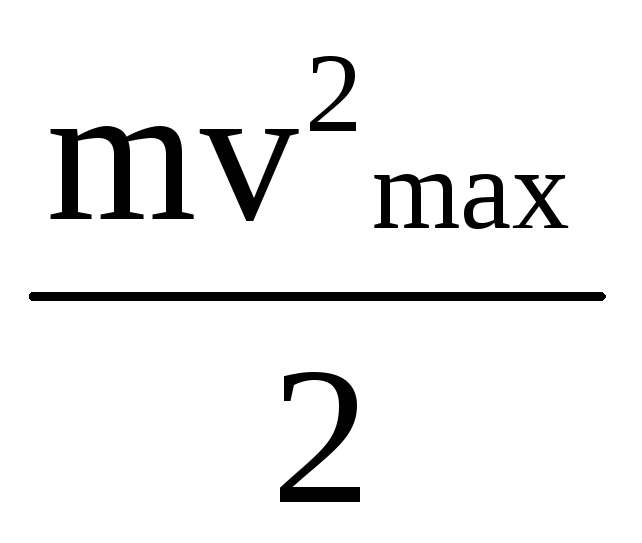
Видно, что максимальная скорость фотоэлектронов, так же как и задерживающий потенциал зависят от частоты света и работы выхода электронов из металла, и не зависят от интенсивности светового потока.
Максимальная начальная энергия фотоэлектрона обращается в нуль при значении частоты света
соответствующей красной границе фотоэффекта. Учитывая, что частота 




Фотоэффект безинерционен, т.е. фототок начинается сразу же как на катод попадает свет с частотой ν ≥ νкр , тогда как по классическим волновым представлениям требуется довольно значительное время для того, чтобы электромагнитная волна заданной интенсивности могла передать электрону энергию , достаточную для совершения работы выходы.
При очень больших интенсивностях света, достижимых в настоящее время с помощью лазеров, наблюдается многофотонный фотоэффект, когда электрон может одновременно получить энергию не одного, а N фотонов. Для этого случая
и красная граница фотоэффекта
Как найти скорость фотоэлектронов
КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА
Найти максимальную скорость фотоэлектронов, вырываемых с поверхности металла светом с длиной волны λ = 180 нм . Красная граница фотоэффекта λ0 = 275 нм
Дано:
Решение:
Зная красную границу фотоэффекта, найдем работу выхода
Уравнение Эйнштейна для внешнего фотоэффекта
Откуда максимальная кинетическая энергия
Максимальная скорость фотоэлектронов
Ответ:

Фотоэффект в физике и его применение — формулы и определение с примерами
На основе волновой теории света можно предположить, что:
- – свет любой длины волны должен вырывать электроны из металла;
- – на вырывание электрона из металла требуется определенное время;
- – число вырванных электронов и их энергия должны быть пропорциональны интенсивности света.
Александр Григорьевич Столетов (1839–1896) – русский физик. Исследовал внешний фотоэффект, открыл первый закон фотоэффекта. Исследовал газовый разряд, критическое состояние, получил кривую намагничивания железа.
Современная установка для исследования фотоэффекта
Современная установка для изучения фотоэффекта представляет собой два электрода, помещенных в стеклянный баллон, из которого выкачан воздух (рис. 210). На один из электродов через кварцевое «окошко» падает свет. В отличие от обычного стекла кварц пропускает ультрафиолетовое излучение. На электроды подается напряжение, которое можно менять с помощью потенциометра R и измерять вольтметром V. К освещаемому электроду К − катоду подсоединяют отрицательный полюс батареи. Под действием света катод испускает электроны, которые направляются электрическим полем к аноду, создается электрический ток. Значение силы тока фиксируется миллиамперметром.
Законы фотоэффекта Столетова
Исследования, проведенные русским ученым А.Г. Столетовым и немецким ученым Ф. Ленардом, показали, что законы фотоэффекта не соответствуют классическим представлениям.
На рисунке 211 представлена вольтамперная характеристика, полученная в результате измерений при различных значениях напряжения между электродами.
Из графика следует, что:
1. Сила фототока не зависит от напряжения, если оно достигает некоторого значения
Максимальное значение силы тока 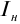
Сила тока насыщения − это максимальный заряд, переносимый фотоэлектронами за единицу времени:
где n − число фотоэлектронов, вылетающих с поверхности освещаемого металла за 1 с, е − заряд электрона.
2. Сила фототока отлична от нуля при нулевом значении напряжения.
3. Если изменить направление электрического поля, соединив катод с положительным полюсом источника тока, а анод − с отрицательным, то скорость фотоэлектронов уменьшится, об этом можно судить по показаниям миллиамперметра: сила тока уменьшается при увеличении отрицательного значения напряжения. При некотором значении напряжения 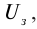
При известном значении 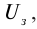
Исследование фотоэффекта при освещении катода световыми потоками равной частоты, но различной интенсивности дал результат, представленный вольтамперными характеристиками, изображенными на рисунке 212.
Сила фототока насыщения увеличивается с увеличением интенсивности падающего света.
Вспомните! Фотоэффект – это испускание электронов веществом под действием света или любого другого электромагнитного излучения.
Величина запирающего напряжения от интенсивности света не зависит, для всех потоков она имеет одно и то же значение.
Освещение катода светом одной и той же интенсивности, но разной частоты дало серию вольтамперных характеристик, представленных на рисунке 213. Как следует из графиков, величина задерживающего напряжения 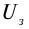
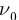
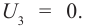
Минимальную частоту падающего света 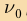
На основании экспериментальных данных Столетовым были сформулированы законы фотоэффекта:
- Сила фототока прямо пропорциональна интенсивности светового потока.
- Максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от интенсивности.
- Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света
(максимальная длина
), при которой возможен фотоэффект, если
то фотоэффект не происходит.
Квантовая теория фотоэффекта
Теоретическое обоснование фотоэффекта было дано в 1905 г. А. Эйнштейном. Он предположил, что свет не только излучается квантами, как утверждал М. Планк, но и распространяется и поглощается порциями, представляет собой поток частиц − фотонов, энергия которых равна
Сам фотоэффект состоит в том, что световые частицы, сталкиваясь с электронами металла, передают им свою энергию и импульс и сами при этом исчезают. Если энергия квантов падающего света больше той работы, которую электрон должен совершить против сил притяжения к положительно заряженным частицам вещества, то электрон вылетает из металла. Становится понятным смысл красной границы фотоэффекта: для вырывания электрона из металла энергия квантов должна быть не меньше, чем 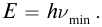
Это и есть формула Эйнштейна для фотоэффекта. Обычно ее пишут в виде:
Зависимость силы фототока от интенсивности света Эйнштейн объяснил следующим образом: число вылетающих в единицу времени электронов пропорционально интенсивности света, поскольку интенсивность определяется числом квантов, испускаемых источником в единицу времени. Мощная лампа испускает больше квантов, следовательно, число вырванных электронов светом такой лампы будет больше, чем светом менее мощной лампы.
Энергия вылетающих электронов зависит не от силы света лампы, а от того, какой частоты свет она испускает, от этого зависит энергия фотона и кинетическая энергия фотоэлектрона.
Фотоны, энергия, масса и импульс фотона
Фотон – это частица света. Он не делится на части: испускается, отражается, преломляется и поглощается целым квантом. У него нет массы покоя, неподвижных фотонов не существует.
Энергия фотона
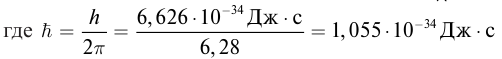
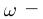
Масса фотона
Массу фотона определяют, исходя из закона о взаимосвязи массы и энергии:
Измерить массу фотона невозможно, ее следует рассматривать как полевую массу, обусловленную тем, что электромагнитное поле обладает энергией.
Импульс фотона
Фотон – частица света, следовательно, ее импульс равен:
Применение фотоэффекта в технике
Фотоэлементы:
Приборы, принцип действия которых основан на явлении фотоэффекта, называют фотоэлементами. Устройство фотоэлемента изображено на рисунке 214. Внутренняя поверхность К (катод) стеклянного баллона, из которого выкачан воздух, покрыта светочувствительным слоем с небольшим прозрачным для света участком для доступа света внутрь баллона. В центре баллона находится металлическое кольцо А (анод). От электродов сделаны выводы для подключения фотоэлемента к электрической цепи. В качестве светочувствительного слоя обычно используют напыленные покрытия из щелочных металлов, имеющих малую работу выхода, т.е. чувствительных к видимому свету.
Фотоэлементы используют для автоматического управления электрическими цепями с помощью световых пучков.
Фотореле:
Фотоэлектрическое реле срабатывает при прерывании светового потока, падающего на фотоэлемент (рис. 215). Фотореле состоит из фотоэлемента Ф, усилителя фототока, в качестве которого используют полупроводниковый триод, и электромагнитного реле, включенного в цепь коллектора транзистора. Напряжение на фотоэлемент подают от источника тока 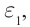
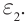
Когда фотоэлемент освещен, в его цепи, содержащей резистор R, идет слабый ток, потенциал базы транзистора выше потенциала эмиттера, и ток в коллекторной цепи транзистора отсутствует.
Если же поток света, падающий на фотоэлемент, прерывается, ток в его цепи сразу прекращается, переход эмиттер – база открывается для основных носителей, и через обмотку реле, включенного в цепь коллектора, пойдет ток. Реле срабатывает, и его контакты замыкают исполнительную цепь. Ее функциями могут быть остановка пресса, в зону действия которого попала рука человека, выдвигание преграды в турникете метро, автоматическое включение освещения на улицах.
Пример решения задачи
Определите постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой 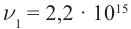
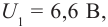
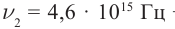
Дано:
Решение: Запишем уравнение Эйнштейна для электрона, вырванного из металла светом с частотами 
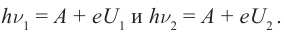
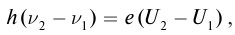
Выполним расчеты:
Ответ: h = 6,6 · 10 –34 Дж · с.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Измерение расстояния до объекта и его скорости
Время на прочтение
9 мин
Количество просмотров 54K
Технологию, которую я собираюсь Вам представить, я не встречал в найденных мной методах определения расстояния до объекта на изображении. Она не является ни универсальной, ни сложной, суть её заключается в том, что видимое поле (будем считать, что мы используем видеокамеру) калибруется линейкой и затем сопоставляется координата объекта на изображении с отметкой на линейке. То есть измерение ведётся по одной линии или оси. Но нам не нужно хранить отметку на линейке для каждого пикселя, алгоритму для калибровки нужно только знать размер линейки в пикселях и в метрах, а также координату пикселя, который является фактической серединой линейки. Очевидное ограничение — работает только на плоских поверхностях.
Кроме самого метода в статье рассмотрена его реализация на языке Python с использованием библиотеки OpenCV, а также рассмотрены особенности получения изображений с вебкамер в Linux, используя video4linux2 API.
На практике нужно было измерить расстояние до автомобиля и его скорость на каком-нибудь прямом участке дороги. Я использовал длинную рулетку, растягивал её в доль дороги, по середине полотна, затем настраивал камеру так, чтобы вся рулетка как раз входила в поле зрение камеры и была выравнена с осью X изображения. Следующим шагом было положить что-нибудь яркое на середину рулетки, закрепить камеру так, чтобы она никуда не съехала, и записать координаты пикселя этой середины.
Все расчёты сводятся к одной единственной формуле:
l = L*K / ( W/x — 1 + K ), где
l – искомое расстояние до объекта, м;
L – длина «линейки», м;
W – длина «линейки» в пикселях, обычно совпадает с шириной изображения;
x – координата объекта на изображении;
K = (W — M) / M – коэффициент, отражающий наклон камеры, здесь M – координата середины «линейки».
В выводе этой формулы мне очень пригодились школьные знания тригонометрии.
График зависимости этой функции приведён на рисунке:
Чем больше наклон камеры, тем круче идёт график. В граничном случае, когда ось камеры направлена перпендикулярно плоскости «линейки» ( M = W / 2), график становится прямой линией.
Но статья была бы слишком короткой, если бы на этом и остановиться. Поэтому я решил сделать демонстрационную программу, которая бы подключалась к вебкамере компьютера и следила бы за каким-нибудь объектом, вычисляя расстояние до него и его скорость. В качестве языка программирования я выбрал Python, язык с очень большим количеством достоинств, для построения графического интерфейса был выбрал фреймворк Tkinter, идущий вместе с Python, так что его не нужно устанавливать отдельно. Для слежения за объектом хорошо подходит OpenCV, я использую версию 2.2, но в репозитории текущей версии ubuntu (10.10) имеется только версия 2.1, а у них API немного изменилось в лучшую сторону и программа под версией 2.1 не заработает. В принципе можно было бы построить всю программу на OpenCV, возложив на неё функции графического интерфейса и захвата изображения, но я хотел отделить её от основной части программы, чтобы можно было если что заменить эту библиотеку на что-нибудь другое или просто убрать, выключив слежение. Я начал перерабатывать старую программу, удаляя всё ненужное, и на моё удивление от программы осталось всего несколько строк с непосредственным расчётом расстояния и скорости, что в принципе было логично, так как в оригинале программа не использует графический интерфейс, следит за автомобилем по другому алгоритму да и вместо вебкамеры используется мегапиксельная сетевая камера с подключением по RTSP.
Что касается получения изображений с вебкамеры, то тут не всё так просто. Под Windows программа использует DirectX для подключения к камере через библиотеку VideoCapture, здесь всё достаточно просто. Но под Linux внятных статей об использовании вебкамер из Python очень мало, а те примеры что есть как правило оказываются неработоспособными из-за какой-нибудь очередной смены API. В прошлом я использовал ffmpeg для этих целей и программа была на C, но ffmpeg это немного «по воробьям из пушки», да и дополнительными зависимостями не хотелось отягощать конечную программу. Можно было воспользоваться OpenCV, которая так же использует ffmpeg, но был выбран путь написания собственной обёртки video4linux2 API для Python.
За основу были взяты исходные коды со страницы какого-то факультета науки. Из них я быстро удалил всё ненужное для моей цели, в итоге оставив два отредактированных файла: V4L2.cpp и V4L2.h. Это собственно и есть минимально необходимое API для подключения к вебкамере. В ходе работы над обёрткой для Python я выяснил, что к video4linux2 устройствам можно обращаться тремя способами: READ, MMAP и STREAM, но с моими вебкамерами работает только MMAP метод. Как выяснилось другие примеры программ, которые у меня не заработали, использовали метод READ.
Также подразумевается, что вебкамера отдаёт изображение в YUYV формате (YUV422), от RGB он отличается тем, что цветовой информации в нём в 2 раза меньше. В YUYV два пикселя кодируются 4 байтами, а в RGB шестью, отсюда экономия в полтора раза. Y — компонента яркости, для каждого пикселя она своя. U и V — цветоразностные компоненты, которые определяют цвет пикселя, так вот каждые два пикселя используют одни и те же значения U и V. Если представить поток байт от вебкамеры в этих обозначениях, то он будет выглядеть как YUYV YUYV YUYV YUYV YUYV YUYV — это 12 пикселей. Выяснить в каком формате у Вас работает вебкамера можно с помощью VLC плеера, открываете захватывающее устройство с его помощью и затем запрашиваете информацию о кодеке, должно быть как на рисунке:
Вот так выглядит исходный код библиотеки для доступа к вебкамере:
main_v4l2.cpp
#include "V4L2.h"
#include <cstring>
#include <iostream>
using namespace std;
extern "C" {
// Specify the video device here
V4L2 v4l2("/dev/video0");
unsigned char *rgbFrame;
float clamp(float num) {
if (num < 0) num = 0;
if (num > 255) num = 255;
return num;
}
// Convert between YUV and RGB colorspaces
void yuv2rgb(unsigned char y, unsigned char u, unsigned char v, unsigned char &r, unsigned char &g, unsigned char &b) {
float C = y - 16;
float D = u - 128;
float E = v - 128;
r = (char)clamp(C + ( 1.402 * E )) ;
g = (char)clamp(C - ( 0.344136 * D + 0.714136 * E )) ;
b = (char)clamp(C + ( 1.772 * D )) ;
}
unsigned char *getFrame() {
unsigned char *frame = (unsigned char *)v4l2.getFrame();
int i = 0, k = 0;
unsigned char Y, U, V, R, G, B;
for (i=0;i<640*480*2;i+=4) {
Y = frame[i];
U = frame[i+1];
V = frame[i+3];
yuv2rgb(Y, U, V, R, G, B);
rgbFrame[k] = R; k++;
rgbFrame[k] = G; k++;
rgbFrame[k] = B; k++;
Y = frame[i+2];
yuv2rgb(Y, U, V, R, G, B);
rgbFrame[k] = R; k++;
rgbFrame[k] = G; k++;
rgbFrame[k] = B; k++;
}
return rgbFrame;
}
void stopCapture() {
v4l2.freeBuffers();
}
// Call this before using the device
void openDevice() {
// set format
struct v4l2_format fmt;
CLEAR(fmt);
fmt.type = V4L2_BUF_TYPE_VIDEO_CAPTURE;
// Adjust resolution
fmt.fmt.pix.width = 640;
fmt.fmt.pix.height = 480;
fmt.fmt.pix.pixelformat = V4L2_PIX_FMT_YUYV;
if (!v4l2.set(fmt)) {
fprintf(stderr, "device does not support used settings.n");
}
v4l2.initBuffers();
v4l2.startCapture();
rgbFrame = (unsigned char *)malloc(640*480*3);
}
}
Алгоритм вполне понятен — сначала открываем устройство, имя которого задаётся вначале («/dev/video0»), а затем на каждый запрос getFrame считываем кадр с вебкамеры, конвертируем его в RGB формат и отдаём ссылку на кадр тому, кто его просил. Я предоставляю также Makefile для быстрой компиляции данной библиотеки, если вам это понадобится.
А вот так выглядит обёртка этой библиотеки для Python:
v4l2.py
from ctypes import *
import Image
import time
lib = cdll.LoadLibrary("linux/libv4l2.so")
class VideoDevice(object):
def __init__(self):
lib.openDevice()
lib.getFrame.restype = c_void_p
def getImage(self):
buf = lib.getFrame()
frame = (c_char * (640*480*3)).from_address(buf)
img = Image.frombuffer('RGB',
(640, 480),
frame,
'raw',
'RGB',
0,
1)
return img, time.time()
Как видите абсолютно ничего сложного. Библиотека подключается с помощью модуля ctypes. В написании обёртки не было никаких проблем, за исключением строчки:
frame = (c_char * (640*480*3)).from_address(buf)
К которой я не сразу пришёл. Дело в том, что если считывать данные из getFrame() как c_char_p, то ctypes будет интерпретировать данные как строку с нулевым окончанием, то есть как только в потоке байт встретится ноль — считывание прекратится. Такая же конструкция позволяет чётко задать сколько необходимо считать байт. В нашем случае это всегда фиксированная величина — 640*480*3.
Я не буду здесь приводить исходный код для получения изображения в Windows, но он так же не отличается какой бы то ни было сложностью и расположен он в архиве в папке windows с именем directx.py.
А приведу я лучше исходный код класса слежения за объектом, который, я напоминаю, написан с использованием OpenCV. Я взял за основу пример lkdemo.py, поставляемый вместе с OpenCV и опять же упростил его для наших нужд, походу переделав его в класс:
tracker.py
class Tracker(object):
"Simple object tracking class"
def __init__(self):
self.grey = None
self.point = None
self.WIN_SIZE = 10
def target(self, x, y):
"Tell which object to track"
# It needs to be an array for the optical flow calculation
self.point = [(x, y)]
def takeImage(self, img):
"Loads and processes next frame"
# Convert it to IPL Image
frame = cv.CreateImageHeader(img.size, 8, 3)
cv.SetData(frame, img.tostring())
if self.grey is None:
# create the images we need
self.grey = cv.CreateImage (cv.GetSize (frame), 8, 1)
self.prev_grey = cv.CreateImage (cv.GetSize (frame), 8, 1)
self.pyramid = cv.CreateImage (cv.GetSize (frame), 8, 1)
self.prev_pyramid = cv.CreateImage (cv.GetSize (frame), 8, 1)
cv.CvtColor (frame, self.grey, cv.CV_BGR2GRAY)
if self.point:
# calculate the optical flow
new_point, status, something = cv.CalcOpticalFlowPyrLK (
self.prev_grey, self.grey, self.prev_pyramid, self.pyramid,
self.point,
(self.WIN_SIZE, self.WIN_SIZE), 3,
(cv.CV_TERMCRIT_ITER|cv.CV_TERMCRIT_EPS, 20, 0.03),
0)
# If the point is still alive
if status[0]:
self.point = new_point
else:
self.point = None
# swapping
self.prev_grey, self.grey = self.grey, self.prev_grey
self.prev_pyramid, self.pyramid = self.pyramid, self.prev_pyramid
Сначала мы должны сказать ему за какой точкой хотим следить, для этого есть метод target. Затем мы даём ему кадр за кадром с помощью метода takeImage, он в свою очередь конвертирует кадр изображения в понятный ему формат, создаёт необходимые для работы алгоритма изображения, переводит кадр из цветного в оттенки серого и затем скармливает это всё функции CalcOpticalFlowPyrLK, которая считает оптический поток пирамидальным методом Лукаса-Канаде. На выходе этой функии мы получаем новые координаты точки, за которой мы следим. Если точка потерялась, то status[0] будет равен нулю. Оптический поток можно посчитать не только для одной точки. Запустите программу lkdemo.py с вебкамерой и посмотрите как хорошо он обрабатывает множество точек.
Скажу ещё про конвертацию изображения из Python Imaging Library в формат OpenCV, дело в том, что OpenCV для цветных изображений использует другой порядок цветовых компонент — BGR, для полной конвертации надо было бы ещё дополнить код строчкой cv.CvtColor(frame, frame, cv.CV_BGR2RGB), но большинству алгоритмов слежения абсолютно всё равно перепутаны у Вас цветовые компоненты или нет, наш же пример вообще использует только чёрно-белые изображения. Поэтому эту строчку можно не включать в код.
Я также не привожу в статье исходный код класса по непосредственному вычислению расстояния, так как там только простейшая математика. Находится он в файле distance_measure.py.
Осталось только показать исходный код основного скрипта, который формирует графический интерфейс и загружает все остальные модули.
main.py
from distance_measure import Calculator
from webcam import WebCam
from tracker import Tracker
from Tkinter import *
import ImageTk as PILImageTk
import time
class GUIFramework(Frame):
"This is the GUI"
def __init__(self,master=None):
Frame.__init__(self,master)
self.grid(padx=10,pady=10)
self.distanceLabel = Label(self, text='Distance =')
self.distanceLabel.grid(row=0, column=0)
self.speedLabel = Label(self, text='Speed =')
self.speedLabel.grid(row=0, column=1)
self.imageLabel = None
self.cameraImage = None
self.webcam = WebCam()
# M = 510, L = 0.5, W = 640
self.dist_calculator = Calculator(500, 0.5, 640, 1)
self.tracker = Tracker()
self.after(100, self.drawImage)
def updateMeasure(self, x):
(distance, speed) = self.dist_calculator.calculate(x, time.time())
self.distanceLabel.config(text = 'Distance = '+str(distance))
# If you want get km/h instead of m/s just multiply
# m/s value by 3.6
#speed *= 3.6
self.speedLabel.config(text = 'Speed = '+str(speed) + ' m/s')
def imgClicked(self, event):
"""
On left mouse button click calculate distance and
tell tracker which object to track
"""
self.updateMeasure(event.x)
self.tracker.target(event.x, event.y)
def drawImage(self):
"Load and display the image"
img, timestamp = self.webcam.getImage()
# Pass image to tracker
self.tracker.takeImage(img)
if self.tracker.point:
pt = self.tracker.point[0]
self.updateMeasure(pt[0])
# Draw rectangle around tracked point
img.paste((128, 255, 128), (int(pt[0])-2, int(pt[1])-2, int(pt[0])+2, int(pt[1])+2))
self.cameraImage = PILImageTk.PhotoImage(img)
if not self.imageLabel:
self.imageLabel = Label(self, image = self.cameraImage)
self.imageLabel.bind("<Button-1>", self.imgClicked)
self.imageLabel.grid(row=1, column=0, columnspan=2)
else:
self.imageLabel.config(image = self.cameraImage)
# 30 FPS refresh rate
self.after(1000/30, self.drawImage)
if __name__ == '__main__':
guiFrame = GUIFramework()
guiFrame.mainloop()
Как я говорил выше, я выбрал библиотеку Tkinter для создания графического интерфейса, я работал и с другими тулкитами, такими как GTK, QT и, конечно же, wxPython, но их необходимо было ставить дополнительно, в то время как Tkinter работает сразу и он весьма прост в обращении, однако сложного интерфейса на нём, конечно, не создать, но его способностей с лихвой хватает для поставленной задачи. В инициализации класса я создаю сетку grid для расположения в ней других виджетов: двух текстовых полей и одного изображения. С Tkinter мне даже не пришлось отдельно создавать потоки для загрузки изображений с вебкамеры, потомучто есть такой метод after, который позволяет выполнять указанную функцию через определенный промежуток времени. Обновлять текст и изображение у Label можно методом config. Очень просто! Обработка события нажатия кнопки мыши с помощью метода bind переводится методу imgClicked.
Загрузка изображения и его временной отметки осуществляется функцией self.webcam.getImage. Модуль webcam всего лишь навсего загружает соответствующий модуль для работы с вебкамерой в зависимости от того под какой операционной системой сейчас работает программа.
Ещё раз приведу ссылку на архив с программой — distance-measure.
Необходимые пакеты для ubuntu: python, python-imaging, python-imaging-tk, opencv версии 2.2 и build-essential для компиляции обёртки V4L2.
Запускается программа через:
python main.py
Чтобы начать следить за объектом, необходимо на него кликнуть.
На этом всё.
Полезные ссылки
- OpenCV wiki
- Optical Flow
- Video4Linux2
- Цветовая модель YUV
- Краткий обзор Tkinter
Скорость передачи данных
- Главная
- /
- Информатика
- /
- Скорость передачи данных
Скорость передачи данных — объём данных (информации), переданный за единицу времени (как правило 1 секунду). Базовой единицей измерения скорости передачи данных является бит в секунду. Также к базовым единицам можно отнести байт в секунду, который равен 8 битам в секунду. Все остальные единицы измерения скорости передачи данных являются производными от этих двух.
Они образуются при помощи приставок:
- используемых для обозначения десятичных кратных единиц: кило- (103), мега- (106), гига- (109) и т.д.
- используемых для обозначения 2-x кратных единиц — двоичные (бинарные) приставки: киби- (210) , меби- (220), гиби- (230) и т.д.
При этом, к примеру:
1 килобит в секунду = 1×103 = 1000 бит в секунду
1 кибибит в секунду = 1×210 = 1024 бит в секунду
1 кибибит в секунду = 1.024 килобит в секунду
1 килобит в секунду = 0.9765625 кибибит в секунду
1 килобит в секунду ≠ 1024 бит в секунду
Хотя до введения двоичных приставок международной электротехнической комиссией (МЭК) в 1999 году, принято было считать, что 1 килобит равняется именно 1024 бит. Но по сути это было не верно.
К сожалению новый стандарт до сих пор используется не повсеместно и из-за этого могут возникнуть ошибки и недопонимания.
Онлайн конвертер
Чтобы перевести скорость передачи данных из одних единиц измерения в другие, введите значение и выберите единицы измерения скорости.
Онлайн калькулятор
Скорость передачи данных
Объём данных (размер файла) I =
Время передачи данных t =
Скорость передачи данных V =
0
Округление ответа:
Объём данных
Скорость передачи данных V =
Время передачи данных t =
Объём данных (размер файла) I =
0
Округление ответа:
Время передачи данных
Объём данных (размер файла) I =
Скорость передачи данных V =
Время передачи данных t =
0
Округление ответа:
Теория
Как найти скорость передачи данных
Чему равна скорость передачи данных (V), если известен объём переданных данных (I) и время (t), за которое эти данные переданы?
Формула
V = I ⁄ t
Пример
Через некое соединение был передан файл размером 5MB (мегабайт), передача заняла 16 секунд. Необходимо определить скорость передачи данного файла в мегабитах в секунду.
Для начала переведём 5 мегабайт в биты (cм. таблицу ниже):
5MB = 5 ⋅ 8000000 = 40 000 000 бит
Далее считаем по формуле:
V = 40000000/16 = 2 500 000 бит/с
Переводим полученный результат в мегабиты в секунду:
V = 2500000/1000000 = 2.5 Мбит/с
Как найти объём данных
Чему равен объём данных (I), если известны скорость передачи данных (V) и время (t), за которое эти данные переданы?
Формула
I = V ⋅ t
Пример
Скорость передачи данных через ADSL-соединение равна 512000 бит/с. Передача файла заняла 16 секунд. Определим объем файла в килобайтах.
Для начала определим размер переданного файла в битах:
I = 512000 ⋅ 16 = 8192000 бит
Переведём полученный результат в килобайты:
I = 8192000/8000 = 1024 Кбайт
Этот результат верен если 1 Кбайт = 1000 бит. Если же вы производите расчет с устаревшими единицами (1 Кбайт = 1024 бит), то:
I = 8192000/8192 = 1000 Кбайт
А если результат записать в кибибайтах:
I = 8192000/8192 = 1000 КиБ
Как найти время передачи данных
Чему равно время передачи данных (t), если известны объём переданных данных (I) и скорость передачи данных (V):
Формула
t = I ⁄ V
Пример
За сколько секунд скачается файл размером в 1GB (гигабайт), если скорость соединения 2 Мбит/с?
1GB = 8 000 000 000 бит = 8 000 Мбит
t = 8000/2 = 4000 сек
Таблица преобразования единиц скорости передачи данных
| Обозначение RU |
Обозначение EN |
бит в секунду | байт в секунду | перевод в бит/с формула |
перевод в Б/с формула |
|
| бит в секунду | бит/с | bit/s | 1 | 0.125 | 1 | 1⁄8 |
| байт в секунду | Б/с | B/s | 8 | 1 | 8 | 1 |
| килобит в секунду | Kбит/с | kbit/s | 1,000 | 125 | 103 | 1⁄8 × 103 |
| кибибит в секунду | Кибит/с | Kibit/s | 1,024 | 128 | 210 | 27 |
| килобайт в секунду | Кбайт/с | kB/s | 8,000 | 1,000 | 8 × 103 | 103 |
| кибибайт в секунду | КиБ/с | KiB/s | 8,192 | 1,024 | 213 | 210 |
| мегабит в секунду | Мбит/с | Mbit/s | 1,000,000 | 125,000 | 106 | 1⁄8 × 106 |
| мебибит в секунду | Мибит/с | Mibit/s | 1,048,576 | 131,072 | 220 | 217 |
| мегабайт в секунду | Мбайт/с | MB/s | 8,000,000 | 1,000,000 | 8 × 106 | 106 |
| мебибайт в секунду | МиБ/с | MiB/s | 8,388,608 | 1,048,576 | 223 | 220 |
| гигабит в секунду | Гбит/с | Gbit/s | 1,000,000,000 | 125,000,000 | 109 | 1⁄8 × 109 |
| гибибит в секунду | Гибит/с | Gibit/s | 1,073,741,824 | 134,217,728 | 230 | 227 |
| гигабайт в секунду | Гбайт/с | GB/s | 8,000,000,000 | 1,000,000,000 | 8 × 109 | 109 |
| гибибайт в секунду | ГиБ/с | GiB/s | 8,589,934,592 | 1,073,741,824 | 233 | 230 |
| терабит в секунду | Тбит/с | Tbit/s | 1,000,000,000,000 | 125,000,000,000 | 1012 | 1⁄8 × 1012 |
| тебибит в секунду | Тибит/с | Tibit/s | 1,099,511,627,776 | 137,438,953,472 | 240 | 237 |
| терабайт в секунду | Тбайт/с | TB/s | 8,000,000,000,000 | 1,000,000,000,000 | 8 × 1012 | 1012 |
| тебибайт в секунду | ТиБ/с | TiB/s | 8,796,093,022,208 | 1,099,511,627,776 | 243 | 240 |
Ссылки
Тема .
№29 Электродинамика. Квантовая физика (Расчетная задача высокого уровня сложности)
.
04
Скорость изображения в различных оптических системах
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
№29 электродинамика. квантовая физика (расчетная задача высокого уровня сложности)
Решаем задачи
Показать ответ и решение
Из тригонометрии , так как углы малые, то
. Тогда
отношение
По закону Снеллиуса или с учетом малости углов
Тогда см – расстояние от линзы до изображения, если бы система состояла только
из линзы.
Запишем формулу тонкой линзы
Поперечное увеличение
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: Сделан поясняющий рисунок,
записан закон Снеллиуса, записана формула тонкой линзы)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
1) Изобразим ход лучей для момента, когда груз находится в максимальном удалении от главной
оптической оси (точка ). Изображение
получается после двойного прохождения лучами линзы и
отражения в зеркале (см. рис.).
Тогда по формуле тонкой линзы:
Двойка в правой части возникает из-за двойного прохождения лучами линзы. Откуда
2) На рисунке расстояние от грузика до главной оптической оси равно , а расстояние от
изображения до главной оптической оси равно
. ИЗ подобия треугольников
и
можно найти:
Пусть , тогда
Возьмём производную по времени от :
Грузик колеблется с циклической частотой:
При этом колебания описываются уравнением
где – начальная фаза колебаний (в данном случае
). Взяв производную от
получим
где – максимальная скорость грузика. В момент прохождения главной оптической оси
скорость изображения грузика максимальна, значит, можно найти
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сделан поясняющий рисунок,
записана формула токной линзы, записано уравнение колебаний, записана формула циклической
частоты)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
1) Запишем формулу тонкой линзы при отсутствии зеркала:
где – расстояние от линзы до действительного изображения
.
Откуда
2) Пусть см – расстояние между зеркалом и линзы. Так как
, то
является
мнимым предметом для зеркала. Для того, чтобы на экране наблюдалось резкое изображение должно
выполняться равенство:
откуда искомая величина
3) Найдём увеличение линзы:
Скорости изображения, полученного в линзе, и источника
связаны формулой:
При этом зеркало не меняется скорость, следовательно, максимальная скорость изображения на
экране:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
тонкой линзы, записана формула увеличения, сказано при каком условии изображение будет
резким)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Груз на пружине совершает гармонические колебания перпендикулярно главной оптической оси
собирающей линзы с оптической силой 5 дптр (см. рисунок). С помощью этой линзы получено чёткое
изображение груза на экране, находящемся на расстоянии 0,5 м от линзы. Максимальная скорость
изображения равна 1 м/с. Определите максимальную скорость самого груза, считая груз материальной
точкой.
Показать ответ и решение
Пусть расстояние от линзы до предмета , расстояние от линзы до изображения
, увеличение линзы
,
– максимальное значение скорости груза,
– максимальное значение скорости
изображения.
Груз и изображение груза совершают колебания с одинаковой циклической частотой . Так как
колебания груза описываются уравнением:
где – амплитуда,
– начальная фаза.
Отсюда скорость описывается уравнением:
Тогда Если амплитуда колебаний груза равна , а амплитуда колебаний изображения
, то по
формуле увеличения:
Отсюда:
Запишем также формулу тонкой линзы:
где – оптическая сила линзы.
Отсюда:
Тогда объединяя (1) – (3), получим:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формулы тонкой
линзы, связи фокусного расстояния и оптической силы линзы, увеличения, даваемого линзой,
формулы кинематического описания гармонического движения для координаты и скорости
(или формула связи амплитуды колебания координаты с амплитудой колебания скорости)
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Висящий на пружине груз совершает вертикальные колебания, двигаясь перпендикулярно главной
оптической оси линзы с фокусным расстоянием см. На экране, который можно перемещать,
получено изображение груза. При этом максимальная скорость изображения оказалась в 8 раз больше
максимальной скорости груза.
1) Найдите расстояние между грузом и линзой.
2) Найдите фокусное расстояние собирающей линзы, которую надо поместить вплотную к первой
линзе, чтобы максимальная скорость изображения уменьшилась в 4 раза по сравнению с предыдущей.
(«Физтех», 2012)
Показать ответ и решение
1) Запишем формулу тонкой линзы:
где – расстояние от линзы до предмета,
– расстояние от линзы до изображения.
Увеличение равно:
где – скорость изображения,
– скорость предмета.
Так как максимальная скорость изображения оказалась в 8 раз больше максимальной скорости груза,
то , отсюда
Тогда из формулы тонкой линзы:
2) Если расстоянием между линзами можно пренебречь, то оптическая сила системы из двух линз
равна сумме оптических сил линз, то есть
где – оптическая сила первой линзы,
– оптическая сила второй линзы.
Запишем формулу тонкой линзы:
где – расстояние от линзы до предмета,
– расстояние от линзы до изображения.
Увеличение равно:
где – скорость изображения,
– скорость предмета.
Так как максимальная скорость изображения уменьшилась в 4 раза по сравнению с предыдущей, то
максимальная скорость изображения оказалась в 2 раз больше максимальной скорости груза, то есть
, отсюда
Тогда из формулы тонкой линзы:
Отсюда
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения, записана формула оптической силы линзы)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Груз массой 0,1 кг, прикрепленный к пружине жесткостью 0,4 Н/м, совершает гармонические колебания
с амплитудой 0,1 м. При помощи собирающей линзы с фокусным расстоянием 0,2 м изображение
колеблющегося груза проецируется на экран, расположенный на расстоянии 0,5 м от линзы. Главная
оптическая ось линзы перпендикулярна траектории груза и плоскости экрана. Определите
максимальную скорость изображения груза на экране.
Сборник задач «1000 задач»
Показать ответ и решение
При колебаниях выполняется закон сохранения энергии, из которого можно выразить максимальную
скорость груза:
где – амплитуда колебания.
Максимальная скорость на экране изображения расположенном на расстоянии
от линзы,
пропорциональна скорости груза, движущегося на расстоянии от плоскости тонкой линзы и может
быть найдена из подобия треугольников:
По формуле тонкой линзы можно найти
Тогда
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: закон сохранения энергии для
гармонических колебаний, записана формула тонкой линзы, найдено отношение скоростей
изображения и источника)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью
м/с движется точечный источник света. Расстояние между плоскостями см. Центр окружности
находится на главной оптической оси линзы. Фокусное расстояние линзы = 10 см. Найдите скорость
движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в
линзе.
Демоверсия 2019
Показать ответ и решение
Сделаем рисунок:
Согласно формуле тонкой линзы, расстояние от предмета до линзы , расстояние от линзы до
изображения и фокусное расстояние
связаны соотношением
Отсюда расстояние от линзы до изображения составляет
Линейное увеличение для изображения предмета тонкой линзой равно
где – расстояние от главной оптической оси до изображения источника света,
– расстояние от
главной оптической оси до источника света.
Изображение и источник света вращаются относительно главной оптической оси на разных расстояниях,
но с одним и тем же периодом. При движении по окружности скорость может быть найдена
как
Запишем отношение скоростей изображения и источника света и выразим отсюда скорость
изображения
Подставим числа
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула тонкой линзы,
формула увеличения, даваемого линзой, доказано равенство угловых скоростей движения предмета и
его изображения, записаны формулы для угловой и линейной скоростей движения точки, сделан
верный чертеж с указанием хода лучей)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник, находящийся на главной оптической оси собирающей линзы на расстоянии от нее, в
полтора раза большем фокусного, начинает смещаться со скоростью 4 мм/с перпендикулярно оси. С
какой скоростью движется изображение источника?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– растояние от изображения до линзы
– расстояние от предмета до оси
– расстояние от изображения до оси
Возьмем производную по времени
где – скорость изображения,
– скорость источника
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник находится на главной оптической оси собирающей линзы с фокусным
расстоянием 6 см на расстоянии 8 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в
направлении, перпендикулярном оптической оси. С какой скоростью движется изображение
источника?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Перейдем в систему отсчета, связанную с линзой. В ней источник движется со скоростью 3
мм/с.
Увеличение линзы равно:
– скорость предмета относительно линзы
– скорость изображения источника в системе отсчета, связанной с линзой
Чтобы узнать скорость изображения, надо перейти обратно в неподвижную систему отсчета, для
этого необходимо:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник движется со скоростью 2 мм/с вдоль главной оптической оси собирающей линзы с
фокусным расстоянием 8 см. С какой скоростью движется изображение источника в тот момент, когда
источник находится от линзы на расстоянии 10 см?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Возьмем производную по времени
Заметим, что – скорость предмета,
– скорость изображения.
Как найти максимальную скорость фотоэлектронов
КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА
Найти максимальную скорость фотоэлектронов, вырываемых с поверхности металла светом с длиной волны λ = 180 нм . Красная граница фотоэффекта λ0 = 275 нм
Дано:
Решение:
Зная красную границу фотоэффекта, найдем работу выхода
Уравнение Эйнштейна для внешнего фотоэффекта
Откуда максимальная кинетическая энергия
Максимальная скорость фотоэлектронов
Ответ:

Максимальная скорость фотоэлектронов формула
Зная красную границу фотоэффекта, найдем работу выхода
Уравнение Эйнштейна для внешнего фотоэффекта
Откуда максимальная кинетическая энергия
Максимальная скорость фотоэлектронов


Определение и уравнение фотоэффекта
Фотоэффект является одним из примеров проявления корпускулярных свойств света. Вылет электронов из освещенных тел, называется внешним фотоэффектом.
Сущность внутреннего фотоэффекта состоит в том, что при освещении полупроводников и диэлектриков от некоторых атомов отрываются электроны, которые, однако, в отличие от внешнего фотоэффекта, не выходят через поверхность тела, а остаются внутри него. В результате внутреннего фотоэффекта возникают электроны в зоне проводимости и сопротивление полупроводников и диэлектриков уменьшается.
При освещении границы раздела между полупроводниками с различным типом проводимости возникает электродвижущая сила. Это явление называется вентильным фотоэффектом.
Уравнение Эйнштейна для внешнего фотоэффекта
Основным уравнением, описывающим внешний фотоэффект, является уравнение Эйнштейна для внешнего фотоэффекта:
где 
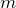
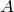
Уравнение фотоэффекта (1) является следствием закона сохранения энергии. В соответствии с законами сохранения энергии и импульса, поглощение фотона свободными электронами невозможно, и фотоэффект возможен только на электронах, связанных в атомах, молекулах и ионах, а также на электронах твердых и жидких тел.
Из уравнения фотоэффекта существует ряд важных выводов, которые характеризуют это явление:
- Для данного фотокатода максимальная начальная скорость фотоэлектронов зависит от частоты падающего света и не зависит от его интенсивности.
- При постоянном спектральном составе падающего света число фотоэлектронов, вырываемых светом из фотокатода за единицу времени, и фототок насыщения пропорциональны энергетической освещенности фотокатода.
- Для каждого вещества фотокатода существует красная граница фотоэффекта (порог фотоэффекта) – минимальная частота
, при которой еще возможен фотоэффект. Длина волны
, соответствующая частоте
, для большинства металлов находится в ультрафиолетовой части спектра.
Примеры решения задач
Вылет электронов прекратится тогда, когда потенциальная энергия электрона (U) в задерживающем поле станет равной его кинетической энергии (E), то есть:
Запишем уравнение фотоэффекта, в которое входит кинетическая энергия электрона:
Подставим (1.1) в (1.2), получим:

Полагая, что красная граница фотоэффекта соответствует энергии фотонов, при которой скорость вырываемых с металла электронов равна нулю, получим:
Подставим (1.5) в (1.4), получим:
Ответ Искомая в задаче частота света может быть рассчитана по формуле:
| Задание | Металлическую пластинку (работа выхода A) освещают светом с длинной волны  . На какое максимальное расстояние от пластинки (d) может удалиться фотоэлектрон, если вне пластинки создано задерживающее однородное электрическое поле с напряженностью E? . На какое максимальное расстояние от пластинки (d) может удалиться фотоэлектрон, если вне пластинки создано задерживающее однородное электрическое поле с напряженностью E? |
По закону сохранения энергии, работа которую совершает электрическое поле при движении электрона (
Определить максимальную скорость vmax фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ 1 =0,155 мкм; 2) γ-излучением с длиной волны λ 2 =2,47 пм.
Решение . Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта:
Энергия фотона вычисляется по формуле ε = hc / λ , работа выхода А указана в табл. 20 для серебра A =4,7 эВ.
Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена или по классической формуле
или по релятивистской
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е , то может быть применена формула (2); если же ε сравнима по размеру с Е , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3)
1. В формулу энергии фотона ε = hc / λ подставим значения величин h , с и λ и, произведя вычисления, для ультрафиолетового излучения получим
Это значение энергии фотона много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть выражена
по классической формуле (2) ε 1 = A + ½ m v 2 max , откуда
Выпишем величины, входящие в формулу (4): ε 1 =1,28 × 10 -18 Дж (вычислено выше); A =4,7 эВ = 4,7 × 1,6*10 -19 Дж = 0,75*10 -18 Дж; m =9,11 × 10 -31 кг (см. табл. 24).
Подставив числовые значения в формулу (4), найдем максимальную скорость:
2. Вычислим теперь энергию фотона γ-излучения:
Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона:
Так как в данном случае кинетическая энергия электрона сравнима с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии,
Выполнив преобразования, найдем
Сделав вычисления, получим
Следовательно, максимальная скорость фотоэлектронов, вырываемых γ-излучением,
как найти максимальную скорость фотоэлектронов?? Срочно)) очень) формулу)
такс) это все онечно круто и подробно) но че-т я после дикого дня не соображаю уже) можно попросить вас решить?) 1) Работа выхода электронов из кадмия равна 4,08 эВ. Какова частота света, если максимальная скорость фотоэлектронов 7,2 • 105 м/с?
2) Каково задерживающее напряжение для электронов, вырванных ультрафиолетовым излучением с длиной волны 0,1 мкм из вольфрамовой пластины?
3) Какова максимальная скорость фотоэлектронов, вылетающих при действии на поверхность цинка ультрафиолетового излучения с длиной волны 150 нм? 4) Падающий на поверхность катода желтый свет вызывает фотоэффект. Обязательно ли возникнет фотоэффект при освещении катода синим светом? оранжевым светом? 5). Какова максимальная скорость фотоэлектронов при действии на катод света длиной волны 450 нм, если красная граница фотоэффекта для данного катода 600 нм? если можно, не только ответы)




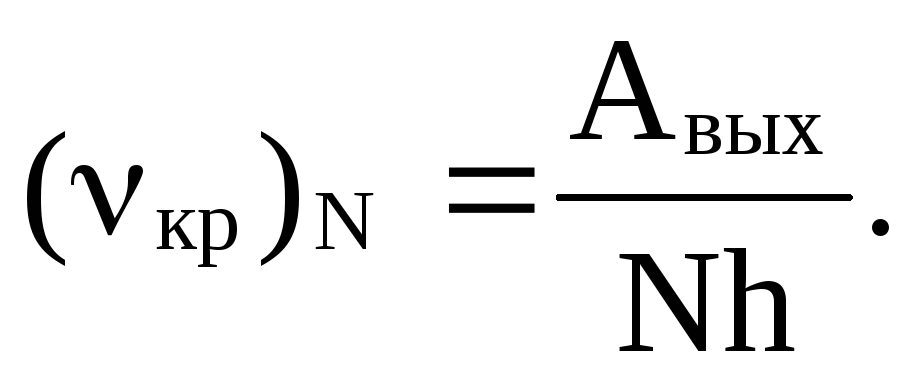






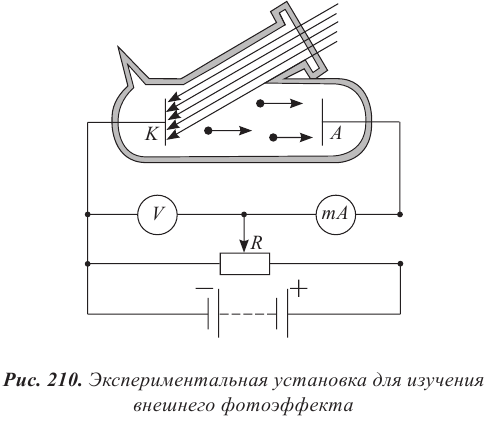
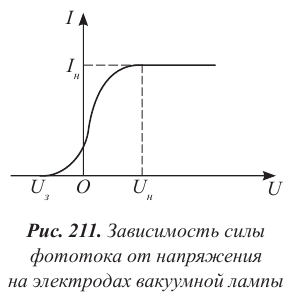
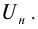
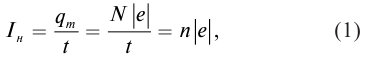
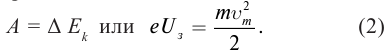
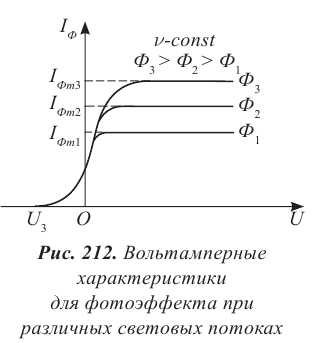
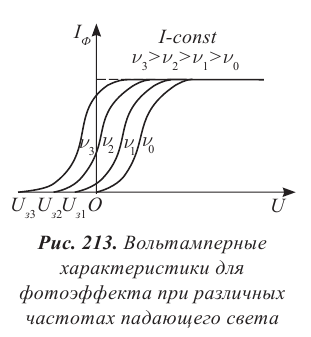
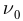 (максимальная длина
(максимальная длина 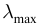 ), при которой возможен фотоэффект, если
), при которой возможен фотоэффект, если 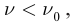 то фотоэффект не происходит.
то фотоэффект не происходит.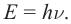

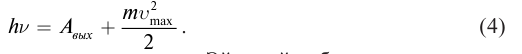



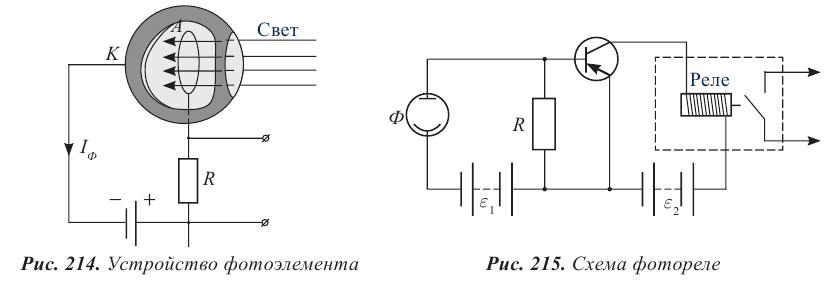
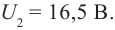
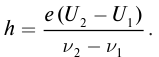
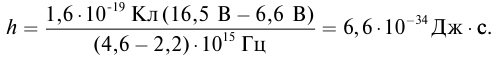

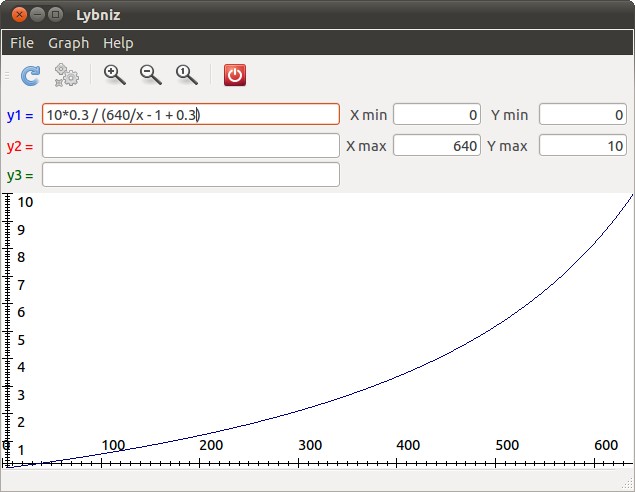
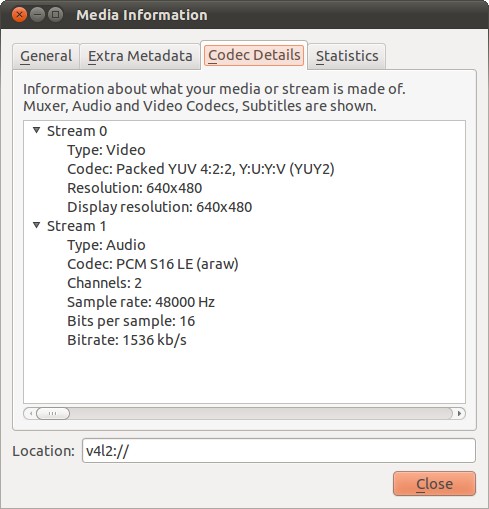
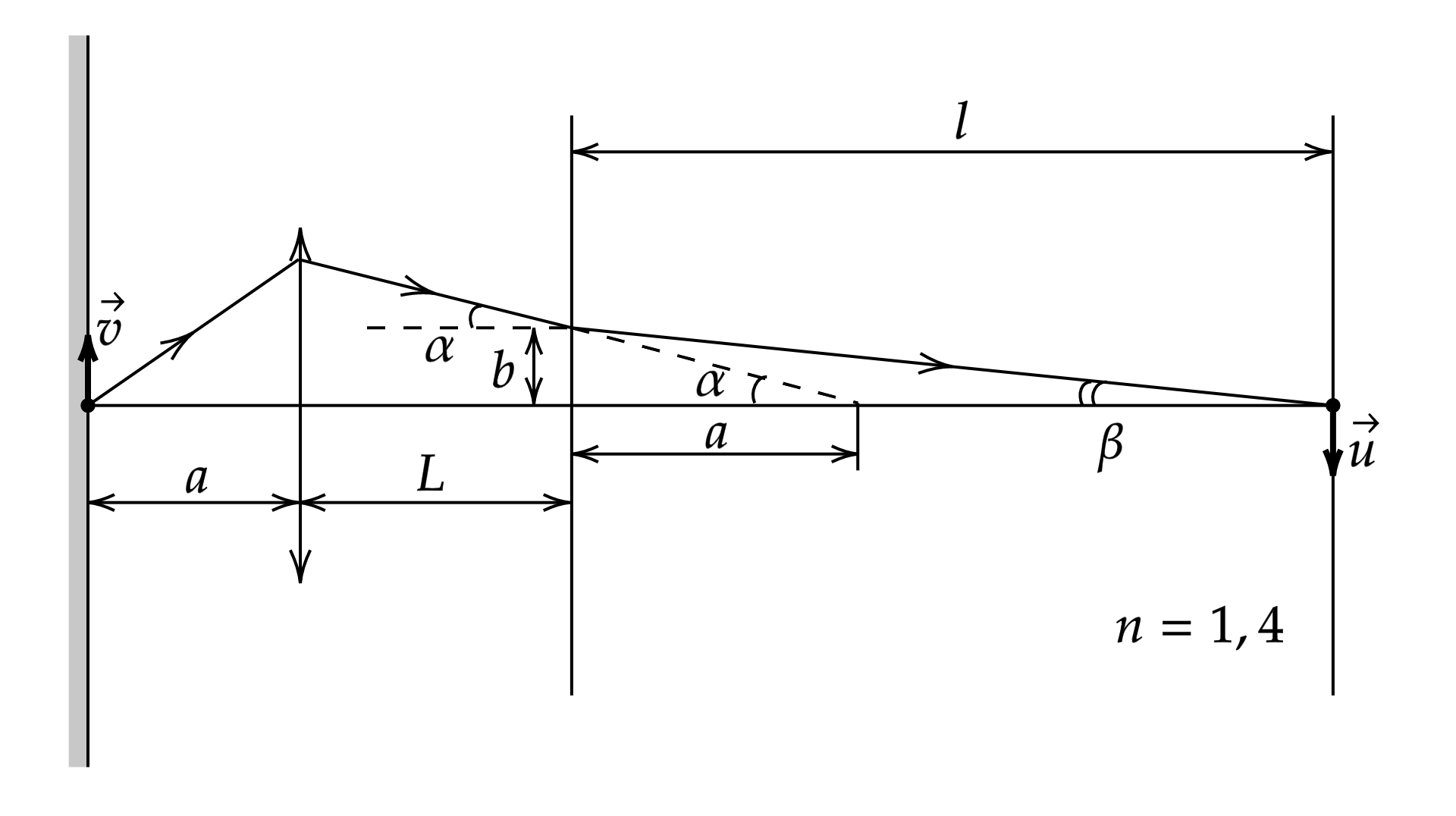
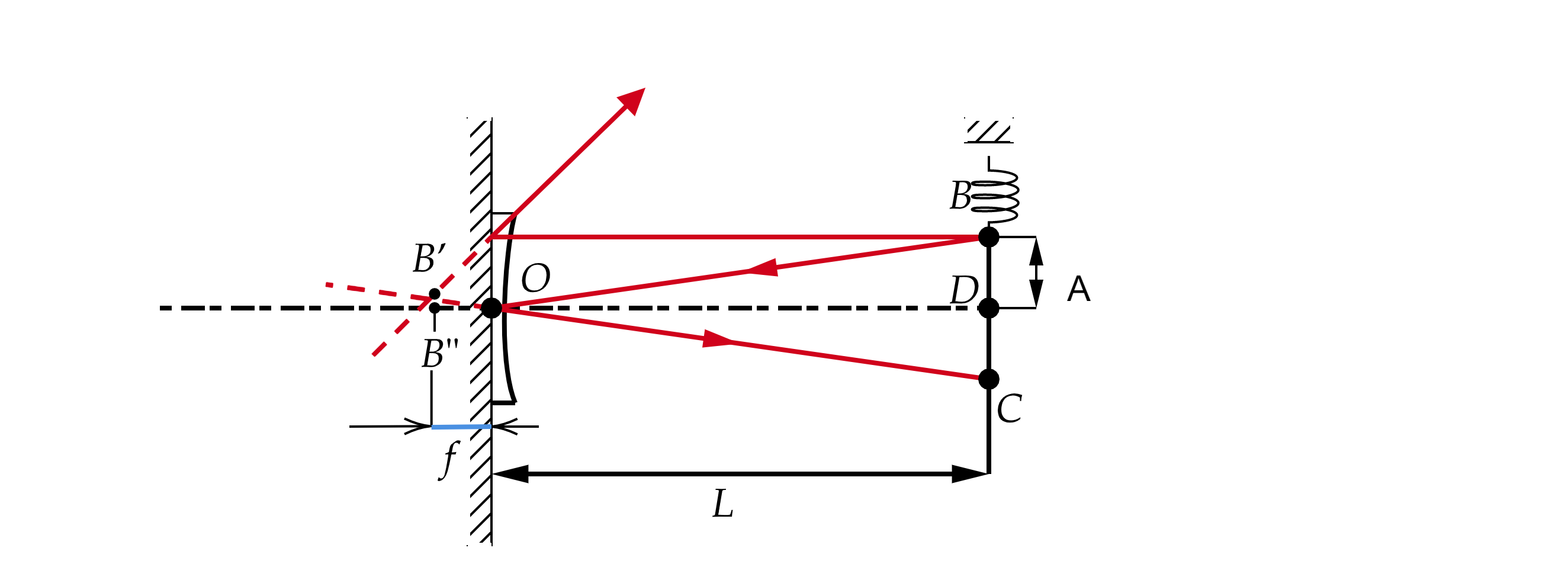
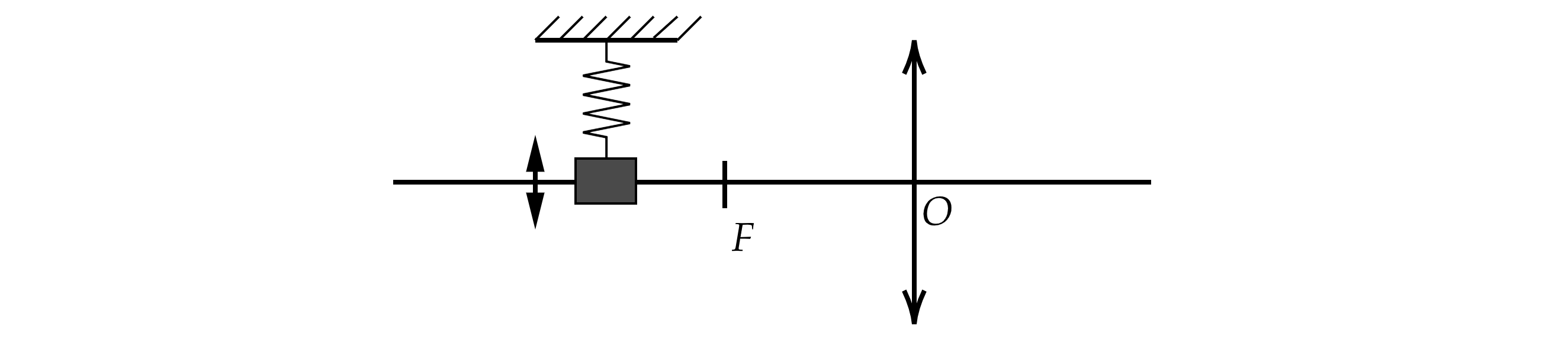
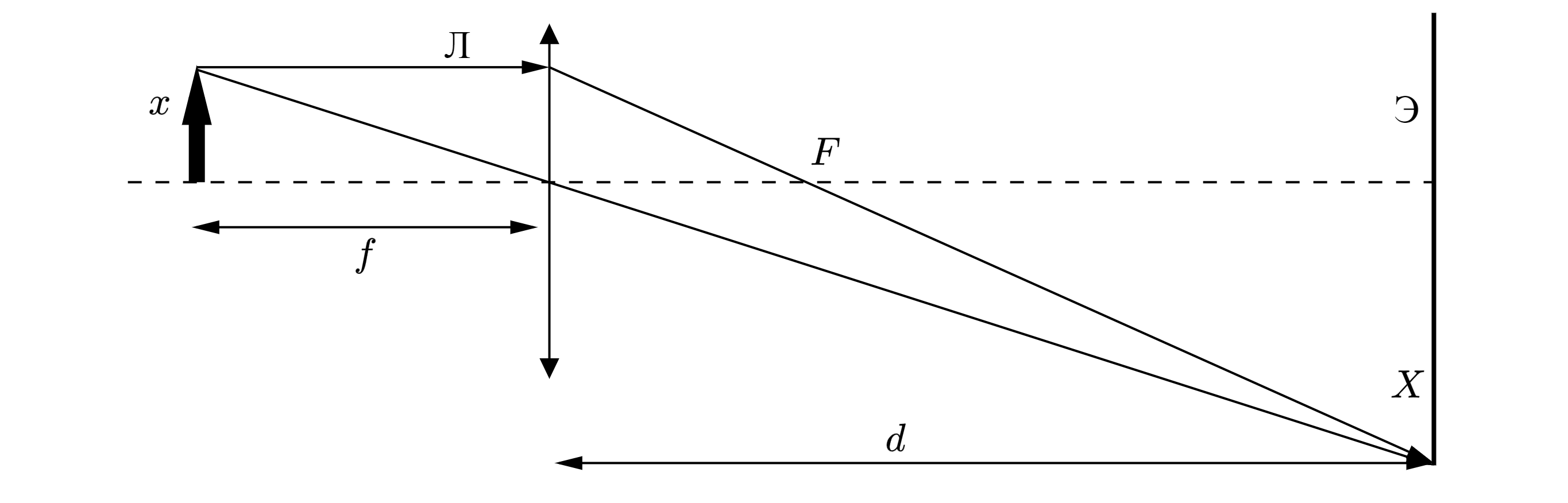
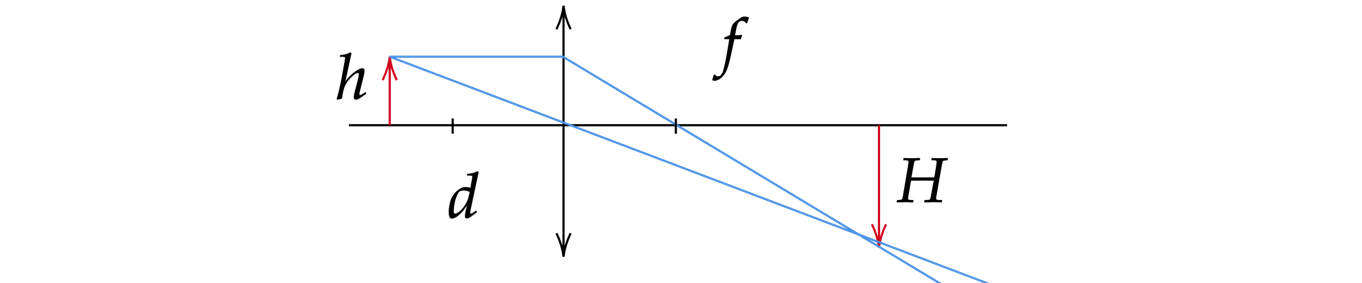






 , при которой еще возможен фотоэффект. Длина волны
, при которой еще возможен фотоэффект. Длина волны  , соответствующая частоте
, соответствующая частоте  , для большинства металлов находится в ультрафиолетовой части спектра.
, для большинства металлов находится в ультрафиолетовой части спектра.






