Одинаковое расстояние можно проехать за разное время.
Например, спортивная машина один километр может проехать быстрее, чем тяжело нагруженная грузовая машина. Одна и та же машина может ехать как быстрее, так и медленнее.
Обрати внимание!
Чтобы сравнить различные движения, необходимо знать скорость движения.
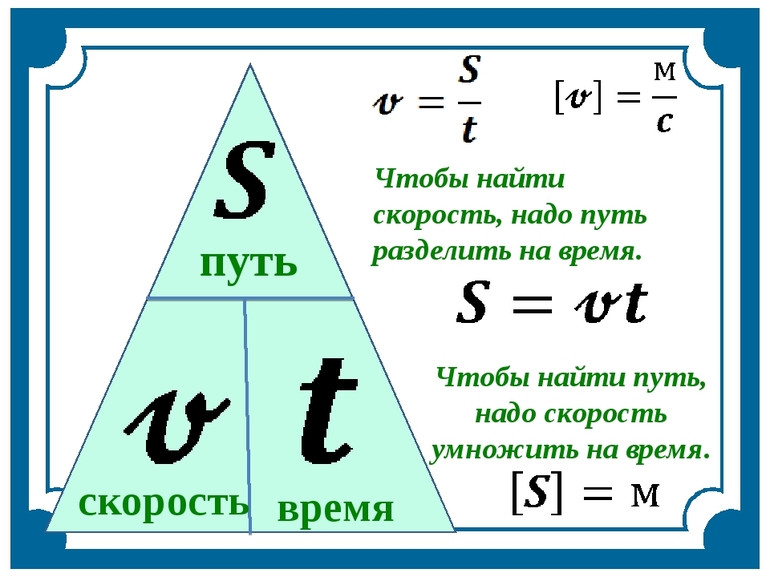
Скоростью движения называется величина, численно равная пути, проходимому телом в единицу времени.
Скорость вычисляется по формуле
v=st
, где
(s) — пройденный путь;
(t) — время.
Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с).
Метр в секунду (м/с) — единица скорости в международной системе единиц.
Скорость можно выражать и в других единицах, например в км/с или в км/ч.
Различные примеры скорости:
1. скорость реактивного самолета — 3000 км/ч.
2. Скорость спринтера на дистанции — 37 км/ч.
3. Скорость звука в воздухе — 1224 км/ч.
4. Средняя скорость ходьбы — 6 км/ч.
5. Максимальная скорость гепарда — 114 км/ч.
6. Скорость улитки — 0,02 км/ч.
Механическое движение имеет множество характеристик. Вы уже узнали, что оно относительно и бывает разных видов: прямолинейное и криволинейное, равномерное и неравномерное.
Тела движутся по воображаемым линиям, которые называются траекториями, а длина траектории – это путь, который проходит тело.
В этом уроке мы рассмотрим новую физическую величину, характеризующую движение – скорость.
Скорость при равномерном движении
Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?
В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь в физике появляется такая величина, как скорость.
Скорость – это физическая величина, характеризующая быстроту движения тел.
В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, то есть движутся с различными скоростями.
Что показывает скорость при равномерном движении?
Скорость при равномерном движении тела показывает, какой путь проходит тело в единицу времени.
Скорость при равномерном движении постоянна.
Как вычислить скорость
По какой формуле определяют скорость тела, если известен его путь и время, за которое он пройден?
Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:
$Скорость = frac{Путь}{Время}$
или
$upsilon = frac{S}{t}$.
Здесь $upsilon$ — скорость, $S$ – путь, $t$ — время.
Дадим определение.
Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.
Соответственно, если автомобиль проезжает в течение 10 с путь, равный 20 метрам (рисунок 2), то его скорость будет равна $frac{20 space м}{10 space с} = 2 frac{м}{с}$ (2 метра в секунду).
Скорость при неравномерном движении
При неравномерном движении тело проходит разные пути за равные промежутки времени, т.е. скорость тела изменяется от одного участка пути к другому.
Как же определить скорость на всем пути? Здесь нам поможет понятие средней скорости.
Как определяют среднюю скорость при неравномерном движении?
Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:
$upsilon_{ср} = frac{S}{t}$.
Отметим, что средняя скорость описывает движение тела за весь промежуток времени. В это время тело можно замедляться, разгоняться, останавливаться.
Например, если вы выезжаете на автомобиле из Москвы в Санкт-Петербург (рисунок 3), то весь путь займет у вас 10 ч. В это время машина будет то набирать скорость, то тормозить, сделает остановку. Общий путь, который вы при этом проедите, будет равен 600 км.
Средняя скорость движения автомобиля будет равна:
$upsilon_{ср} = frac{S}{t} = frac{600 space км}{10 space ч} = 60 frac{км}{ч}$.
Взгляните на таблицу 1, где приведены различные средние скорости.
| Тело | Скорость, $frac{м}{с}$ | Тело | Скорость, $frac{м}{с}$ |
|---|---|---|---|
| Улитка | 0,0014 | Пассажирский самолет | 220 |
| Черепаха | 0,05-0,14 | Звук в воздухе при $0 degree C$ | 332 |
| Муха | 5 | Пуля автомата Калашникова | 760 |
| Пешеход | 1,5 | Луна вокруг Земли | 1000 |
| Конькобежец | 13 | Молекула водорода при $0 degree C$ | 1693 |
| Скворец | 20 | Молекула водорода при $25 degree C$ | 1770 |
| Страус | 22 | Земля вокруг Солнца | 30 000 |
| Автомобиль | 20 | Свет и радиоволны | 300 000 000 |
Единицы измерения скорости
Какова единица измерения скорости в СИ?
В Международной системе (СИ) скорость измеряется в метрах в секунду $frac{м}{с}$.
За единицу скорости принимают скорость такого равномерного движения, при котором за 1 секунду тело проходит путь длиной 1 метр.
Следственно, скорость в системе СИ — количество метров, которое тело пройдёт за 1 секунду.
В повседневной жизни мы чаще видим, что скорость измеряют в километрах в час $frac{км}{ч}$. Также можно использовать километры в секунду $frac{км}{с}$ и сантиметры в секунду $frac{см}{с}$.
Наиболее часто встречаемое ограничение скорости в городах – $ 60 frac{км}{ч}$. Переведем это значение в $frac{м}{с}$:
$60 frac{км}{ч} = 60 cdot frac{1 space км}{1 space ч} = 60 cdot frac{1000 space м}{3600 space с} = frac{60 cdot 1000}{3600} frac{м}{с} approx 17 frac{м}{с}$
Так мы увидели, что числовое значение скорости зависит от выбранной единицы измерения.
Скорость как вектор
Чем, кроме числового значения, характеризуется скорость тела?
Логично, что, кроме числового значения, скорость имеет и направление. Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.
Физические величины делятся на те, которые имеют направление и те, которые его не имеют — на векторные и скалярные:
1. Векторные величины – это величины, которые, кроме числового значения (модуля), имеют еще и направление.
Скорость – это векторная физическая величина
Векторные величины обозначаются буквами со стрелочками. Скорость обозначается как $vec{upsilon}$, а модуль скорости — $upsilon$.
На рисунке 4 стрелкой показано направление скорости (направление движение тела).
2. Скалярные величины – это физические величины, которые не имеют направления и характеризуются только числовым значением. Это путь, объем, время, длина, масса и др.
Примеры задач на нахождение скорости
Задача №1
Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.
Дано:
$S = 152 space км$
$t = 3 space ч$
$upsilon -?$
Показать решение и ответ
Скрыть
Решение:
Скорость рассчитывается по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{152}{3} frac{км}{ч} approx 51 frac{км}{ч}$.
Выразим в единицах СИ:
$51 frac{км}{ч} = frac{51 000}{3600} frac{м}{c} approx 14 frac{м}{c}$.
Ответ: $upsilon = 14 frac{м}{с}$.
Задача №2
Скорость лыжника первую часть пути составляла $20 frac{км}{ч}$ в течение 15 мин. Следующие 45 мин его скорость была $10 frac{км}{ч}$. Найдите среднюю скорость лыжника.
Обозначим первую часть пути как $s_1$, вторую как $s_2$. Время, соответствующее движению на этих участках, $t_1$ и $t_2$ (рисунок 5). Скорости — $upsilon_1$ и $upsilon_2$.
Дано:
$upsilon_1 = 20 frac{км}{ч}$
$t_1 = 15 space мин$
$upsilon_2 = 10 frac{км}{ч}$
$t_2 = 45 space мин$
$upsilon_{ср} -?$
Показать решение и ответ
Скрыть
Решение:
Скорость лыжника на первой и второй частях пути:
$upsilon_1 = frac{S_1}{t_1}$; $upsilon_2 = frac{S_2}{t_2}$.
Выразим из этих уравнений неизвестные $s_1$ и $s_2$:
$s_1 = upsilon_1t_1$; $s_2 = upsilon_2t_2$.
Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:
$upsilon_{ср} = frac{s_1+s_2}{t_1+t_2} = frac{upsilon_1t_1+upsilon_2t_2}{ t_1+t_2}$.
Выпишем отдельно часть выражения и переведем в часы:
$t_1+t_2 = 15 space мин + 45 space мин = 1space ч$.
Тогда:
$t_1 = frac{1}{4} space ч = 0.25 space ч$,
$t_2 = frac{3}{4} space ч = 0.75 space ч$.
$upsilon_{ср} = frac{20 frac{км}{ч} cdot 0.25 space ч+10 frac{км}{ч} cdot 0.75 space ч}{1 space ч} = frac{5 space км +7.5 space км}{1 space ч} = 12.5 frac{км}{ч}$.
Ответ: $upsilon_{ср} = 12,5 frac{км}{ч}$.
Упражнения
Упражнение №1
Выразите скорости тел: $90 frac{км}{ч}$ и $36 frac{км}{ч}$ в $frac{м}{с}$.
Показать решение
Скрыть
Решение:
$upsilon_1 = 90 frac{км}{ч} = 90 cdot frac{1000 space м}{3600 space с} = frac{1000}{40} frac{м}{с} = 25 frac{м}{с}$.
$upsilon_2 = 36 frac{км}{ч} = 36 cdot frac{1000 space м}{3600 space с} = frac{1000}{100} frac{м}{с} = 10 frac{м}{с}$.
Упражнение №2
Поезд идет со скоростью $72 frac{км}{ч}$. Выразите его скорость в $frac{м}{с}$.
Показать решение
Скрыть
Решение:
$upsilon = 72 frac{км}{ч} = 72 cdot frac{1000 space м}{3600 space с} = frac{1000}{50} frac{м}{с} = 20 frac{м}{с}$.
Упражнение №3
Гоночный автомобиль за $10 space мин$ проезжает путь, равный $50 space км$. Определите его среднюю скорость.
Дано:
$t = 10 space мин$
$S = 50 space км$
СИ:
$t = 600 space с$
$S = 50 space 000 space м$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$.
$upsilon_{ср} = frac{50 space 000 space м}{600 space с} approx 83.3 frac{м}{с}$.
Ответ: $upsilon_{ср} approx 83.3 frac{м}{с}$.
Упражнение №4
Лучшие конькобежцы дистанцию $1500 space м$ пробегают за $1 space мин$ и $52.5 space с$. С какой средней скоростью они проходят эту дистанцию?
Дано:
$t =1 space мин space 52.5 space с$
$S = 1500 space м$
СИ:
$t = 112.5 space с$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$.
$upsilon_{ср} = frac{1500 space м}{112.5 space с} approx 13.3 frac{м}{с}$.
Ответ: $upsilon_{ср} approx 13.3 frac{м}{с}$.
Упражнение №5
Лыжник, спускаясь с горы, проходит $50 space м$ за $5 space с$. Спустившись с горы и продолжая двигаться, он до полной остановки проходит еще $30 space м$ за $15 space с$. Найдите среднюю скорость лыжника за все время движения.
Дано:
$S_1 = 50 space м$
$t_1 = 5 space с$
$S_2 = 30 space м$
$t_2 = 15 space с$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$, где $S$ — весь путь, пройденный лыжником, $t$ — общее время движения.
Общий путь равен: $S = S_1 + S_2$.
Общее время движения: $t = t_1 + t_2$.
Подставим эти значения в формулу для средней скорости и рассчитаем ее:
$upsilon_{ср} = frac{S_1 + S_2}{t_1 + t_2}$,
$upsilon_{ср} = frac{50 space м + 30 space м}{5 space с + 15 space с} = frac{80 space м}{20 space с} = 4 frac{м}{с}$.
Ответ: $upsilon_{ср} = 4 frac{м}{с}$.
Задание
Найдите с помощью интернета фамилии советских летчиков, совершивших впервые в мире беспосадочный перелет Москва-Северный полюс-США. Известно, что расстояние в $8582 space км$ они пролетели за $63 space ч$ и $16 space мин$. Определите, с какой скоростью летел самолет.
Первый беспосадочный перелет Москва-Северный полюс-США совершили советские авиаторы 18-20 июня в 1937 году. Перелет был совершен на самолете АНТ-25. Состав: командир экипажа В. П. Чкалов, второй пилот Г. Ф. Байдуков и штурман А. В. Беляков.
Дано:
$S = 8582 space км$
$t = 63 space ч space 16 space мин$
СИ:
$S = 8 space 582 space 000 space м$
$t = 227 space 760 space с$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость:
$upsilon = frac{S}{t}$,
$upsilon = frac{8 space 582 space 000 space м}{227 space 760 space с} approx 37.7 frac{м}{с}$.
Ответ: $upsilon approx 37.7 frac{м}{с}$.
Загрузить PDF
Загрузить PDF
Скорость — это векторная величина, которая характеризует быстроту перемещения и направление движения предмета (тела). В математике скорость определяется как изменение положения тела в зависимости от изменения времени.[1]
Скорость можно найти во множестве физических и математических задач. Выбор правильной формулы зависит от данных значений, поэтому внимательно читайте условие задачи.
Формулы
-
1
-
2
Запишите формулу, содержащую положение и время. Скорость можно вычислить по изменению положения тела и времени. Такую формулу можно применить к любой задаче. Обратите внимание, что если скорость тела меняется, вы найдете среднюю скорость за все время движения, а не конкретную скорость в определенный момент времени.
-
3
Вычислите расстояние между начальным и конечным положениями. То есть между точками начала и окончания движения; они, наряду с направлением движения, указывают на «перемещение» или «изменение положения».[3]
При этом траектория движения тела между этими точками значения не имеет.-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
- Автомобиль переместился на 41-5 = 36 м на восток.
-
Пример 2: трамплин подбрасывает пловца на 1 метр вверх, и пловец летит до воды 5 м. Каково перемещение пловца?
- Пловец оказался на 4 м ниже начальной точки, поэтому его перемещение равно -4 м (0 + 1 — 5 = -4). Несмотря на то, что пройденное пловцом расстояние составило 6 м (1 м вверх и 5 м вниз), конечная точка находится на 4 м ниже начальной точки.
-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
-
4
Вычислите изменение времени. Время, которое потребовалось для достижения конечной точки, будет, скорее всего, дано в задаче; если нет, просто вычтите начальное время из конечного.
- Пример 1 (продолжение): в задаче сказано, что машине потребовалось 8 с, чтобы переместиться из начальной точки в конечную, поэтому изменение времени равно 8 с.
- Пример 2 (продолжение): если пловец прыгнул в момент времени t = 7 с и коснулся воды в момент времени t = 8 с, изменение времени: 8 — 7 = 1 с.
-
5
Разделите перемещение на изменение времени. Сделайте это, чтобы найти скорость движущегося тела. Теперь укажите направление движения, и вы получите среднюю скорость.
-
6
Решите задачу, когда направление движения меняется. Не во всех задачах тело движется вдоль одной линии. Если тело совершило поворот, нарисуйте схему движения и решите геометрическую задачу, чтобы найти расстояние.
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
- Нарисуйте схему и соедините начальную и конечную точки прямой линией. Это гипотенуза треугольника, которую можно найти с помощью теоремы Пифагора или других формул. В нашем примере перемещение составит 5 м на северо-восток.
- Возможно, учитель математики попросит вас найти точное направление движения (в виде угла над горизонтальной прямой). В этом случае воспользуйтесь геометрическими законами или векторами.[4]
Реклама
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
-
1
Запомните формулу для вычисления скорости ускоряющегося тела. Ускорение — это быстрота изменения скорости. Если ускорение постоянное, скорость меняется с одинаковой быстротой.[5]
Формула включает произведение ускорения и времени, а также начальную скорость: -
2
Умножьте ускорение на изменение времени. Так вы вычислите, насколько скорость увеличилась (или уменьшилась) за это время.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
- a = 10 м/с 2
- t = 5 с
- (a * t) = 10 * 5 = 50 м/с.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
-
3
Прибавьте начальную скорость. Вы нашли общее изменение скорости. Прибавьте это значение к начальной скорости тела, чтобы вычислить конечную скорость.
- Пример (продолжение): какова скорость лодки через 5 с?
-
4
Укажите направление движения. Помните, что скорость является векторной величиной, то есть имеет направление. Поэтому в ответе укажите направление.
- В нашем примере лодка начала движение на север и не изменила направление, поэтому ее конечная скорость равна 52 м/с на север.
-
5
Используйте данную формулу, чтобы вычислить другие величины, которые входят в нее. Если известны ускорение и скорость в определенный момент времени, с помощью формулы можно найти скорость в другой момент времени. Например, вычислим начальную скорость:
- Поезд ускоряется на 7 м/с2 в течение 4 секунд и достигает скорости 35 м/с. Какова начальная скорость поезда?
Реклама
-
1
Запомните формулу для вычисления круговой скорости. Круговая скорость — это скорость, которую должно иметь тело, чтобы постоянно вращаться вокруг другого тела, обладающего гравитацией, например, планеты.[6]
- Круговая скорость равна отношению длины круглого пути к периоду времени, в течение которого тело движется.
- Формула для вычисления круговой скорости:
- v = (2πr) / T
- Обратите внимание, что 2πr — это длина окружности.
- r — радиус.
- T — период времени.
-
2
Умножьте радиус окружности на 2π. Сначала необходимо вычислить длину окружности. Для этого умножьте радиус на 2π. В качестве значения π можно использовать 3, 14.
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
- r = 8 м
- T = 45 с
- Длина окружности = 2πr ≈ (2)(3,14)(8) = 50,24 м
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
-
3
Разделите полученное значение на время. Сделайте это, чтобы вычислить круговую скорость тела.
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
- Круговая скорость тела равна 1,12 м/с.
Реклама
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
Советы
- Метры в секунду (м/с) — это единица измерения скорости.[7]
. Перед решением задачи убедитесь, что все единицы измерения соответствуют друг другу, например, значения даны в метрах (м), секундах (с), метрах в секунду (м/с) и метрах в квадратных секундах (м/с2). - Средняя скорость характеризует среднюю скорость, которую имеет тело на протяжении всего пути. Мгновенная скорость — это скорость тела в определенный момент времени.
Реклама
Об этой статье
Эту страницу просматривали 17 763 раза.
Была ли эта статья полезной?
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
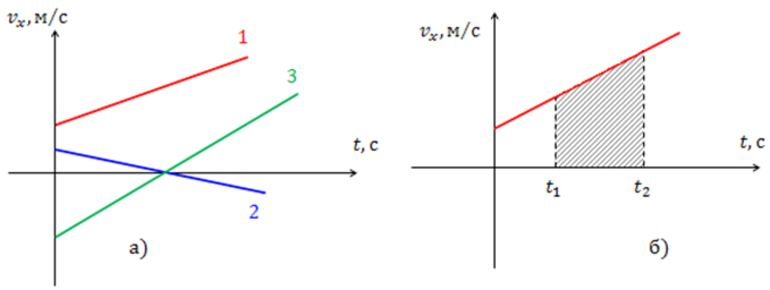
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
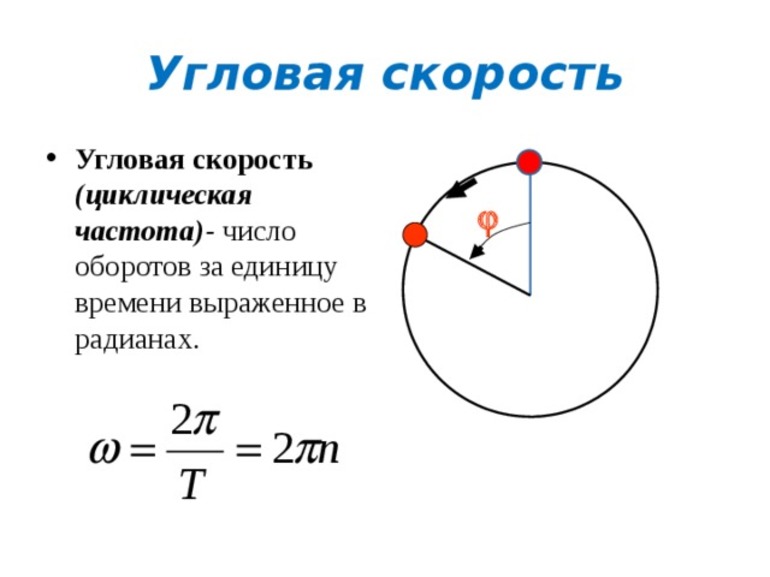
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
- Справочный портал «Калькулятор».
- Allcalc.
- Fxyz.
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Здесь — x нулевое- начальная координата. v нулевое — начальная скорость. Продифференцируем по времени, и получим скорость
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.