Важнейшими характеристиками потоков жидкости или газа (например при движении их в трубах) являются объемный расход и скорость потока.
Объем жидкости, проходящей через заданную площадь за единицу времени. Измеряется в системе СИ в кубических метрах в секунду (м3/с). Обычно обозначается символом QQ.
Скорость движения жидкости, которая численно равна отношению расхода жидкости Q к площади живого сечения.
Понятие расхода
Если через заданную площадь SS жидкость протекает с равномерно распределенной по площади скоростью VV под углом θθ к направлению скорости до перпендикуляра площади SS, то расход составит:
Q=V⋅S⋅cosθQ = V ⋅ S ⋅ cosθ
В частном случае, когда скорость потока перпендикулярна к площади SS, уравнение примет вид:
Q=V⋅SQ = V ⋅ S
Общий случай
Записанные выше уравнения обычно называют уравнениями непрерывности (для одномерных течений несжимаемой жидкости). Если скорость жидкости через заданную площадь неодинакова (или, если область не является плоской), то объемный расход потока жидкости может быть рассчитан с помощью интеграла по площади:
Q=∬Su⋅dωQ = ∬S u ⋅ dω,
где dωdω дифференциал поверхности, который записывается как:
dω=ndSdω = n dS,
где nn – единичный вектор нормали к поверхности; dSdS – дифференциал площади SS.
Полученное уравнение потока вектора скорости через поверхность SS является скалярной величиной. Физически поток вектора скорости представляет собой секундный объемный расход жидкости через поверхность SS.
Измерение скорости потока
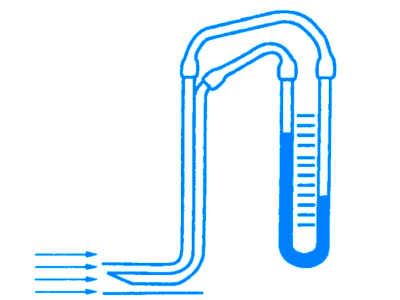
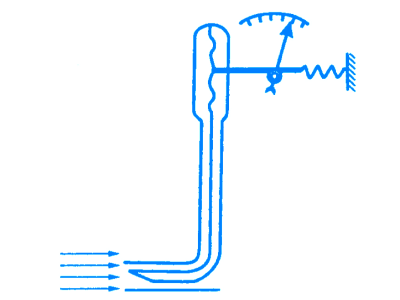
Для измерения скорости потока жидкости или газа используется прибор, предложенный французским ученым А. Пито (1695-1771). Этот прибор имеет две трубки: одну с отверстием напротив потока и вторую с отверстием, параллельным потоку:
Трубки соединены с дифференциальным манометром:
В отверстии первой трубки скорость жидкости или газа равна нулю, а в отверстии второй скорость потока сохраняется. Применив уравнение Бернулли для частиц потока в отверстиях трубок, получим:
p1=ρv22+p2{{p}_{1}}=frac{rho {{v}^{2}}}{2}+{{p}_{2}}
Составляющую ρv2/2ρv^2/2, имеющую размерность давления, называют динамическим давлениям, а составляющую р2р^2 – статичным.
Из уравнения определим скорость потока:
v=2(p1−p2)ρv=sqrt{frac{2({{p}_{1}}-{{p}_{2}})}{rho }}
Здесь ρρ – плотность вещества в потоке; (р1р_1 – р2р_2) находят по разнице высот жидкости в манометре. Согласно данной формуле можно проградуировать манометр в трубке Пито для измерения скорости потока.
Трубку Пито используют для измерения скорости кораблей и самолетов.
Скорость истечения жидкости из бака
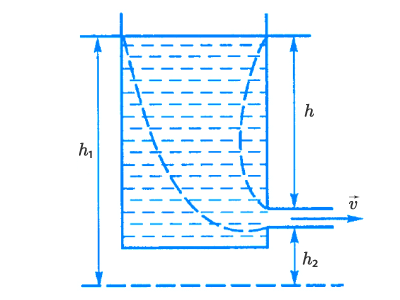
Найдем скорость истечения жидкости из бака:
Для этого выделим в жидкости трубку потока (показанную штриховой линией) и применим к ее сечениям (взятых на поверхности жидкости в баке, и в отверстии утечки) уравнение Бернулли. Если при этом учесть, что давления в обоих сечениях одинаковы и равны атмосферному, а скорость в сечении на поверхности жидкости в баке приравнять к нулю, то получим:
ρgh1=ρv22+ρgh2rho g{{h}_{1}}=frac{rho {{v}^{2}}}{2}+rho g{{h}_{2}}
Отсюда находим vv – скорость истечения жидкости из бака:
v=2g(h1−h2)v=sqrt{2g({{h}_{1}}-{{h}_{2}})}
Поскольку h1−h2=hh_1 — h_2 = h – высота уровня жидкости в баке над отверстием истечения, окончательно:
v=2ghv=sqrt{2gh}
Эту формулу вывел итальянский ученый Э. Торричелли (1608-1647) в 1641 Из нее следует, что скорость истечения жидкости (идеальной) из сосуда такова, какова была бы скорость приобретенная телом, свободно падая с высоты hh.
Цилиндрический сосуд высотой hh = 70 см с площадью дна SS = 600 см2 заполнено водой. В дне сосуда образовалось отверстие S1S_1 = 1 см2. За какое время вытечет вода из сосуда?
Приняв во внимание, что скорость истечения воды из сосуда со временем меняется, поскольку меняется уровень воды, определим сначала ее объем утечки за время dtdt:
dV=S1vdtdV = S_1vdt
где v=2ghv=sqrt{2gh} (hh – уровень воды в заданный момент времени); поэтому:
dV=S12ghdtdV={{S}_{1}}sqrt{2gh}dt
Этот объем утечки можно выразить через снижение уровня воды:
dV=−SdhdV = -Sdh
Если приравнять выражения и разделить переменные, то получим дифференциальное уравнение:
dhh=−S1S2gdtfrac{dh}{sqrt{h}}=-frac{{{S}_{1}}}{S}sqrt{2g}dt
Интегрируя обе части этого уравнения, получаем:
2h=−S1S2gdt+C2sqrt{h}=-frac{{{S}_{1}}}{S}sqrt{2g}dt+C
Найдем постоянную интегрирования. Поскольку при tt = 0, h=h0h = h_0, получим:
Тогда равенство примет вид:
h0−h=S12g2Stsqrt{{{h}_{0}}}-sqrt{h}=frac{{{S}_{1}}sqrt{2g}}{2S}t
В случае полного вытекания воды (hh = 0) равенство примет вид:
t=2SS1h02gt=frac{2S}{{{S}_{1}}}sqrt{frac{{{h}_{0}}}{2g}}
Подставив значения из условия получим
tt = 227 с.
Тест по теме «Скорость потока»
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Воспользовавшись данным калькулятором, вы без труда сможете определить скорость воды в трубе, зная диаметр трубы и расход воды.
Как пользоваться калькулятором для расчёта скорости жидкости в трубопроводе?
Введите диаметр трубы, через которую будет протекать жидкость. Затем заполните следующее поле калькулятора, где укажите расход воды в трубе за единицу времени. После этого останется только нажать на кнопку «Рассчитать» и сразу же узнаете скорость потока жидкости в данном трубопроводе. Как вы можете видеть всё довольно просто и легко.
В итоге, после вычислений, результат скорости будет выведен в метрах в секунду (м/с). Если вам нужны другие единицы измерения, то переводить придётся самостоятельно.
Как самостоятельно определить скорость движения воды в трубе ?
Для того чтобы рассчитать скорость протекания жидкости в трубе воспользуйтесь следующей формулой из гидравлики:
V = 4 * Q / (π * d2) , где
Q — расход воды в трубе, м3/сек,
π — просто число пи (из математики),
d — внутренний диаметр трубопровода, м
Результатом будет скорость движения жидкости в м/с. При вычислениях будьте внимательны в размерностях. А лучше всего скорость воды считайте на нашем простом онлайн-калькуляторе. Это сэкономит ваше время и нервы :).
Максимальная скорость движения жидкости в трубе обычно ограничивается из соображений шумности потока в трубах. Следует придерживаться следующих рекомендаций:
до 1,5 м/сек — скорость для общественных зданий и помещений в них,
до 2,0 м/сек — скорость для административно-бытовых зданий и помещений,
до 3,0 м/сек — максимальная скорость в производственных зданиях и помещениях.
Слишком маленькая скорость тоже противопоказана нормальной работе трубопровода. В некоторых случаях могут образовываться воздушные пробки в системе.
Как м3/ч перевести в л/с ?
Перевести метры кубические в час в литры в секунду или наоборот очень просто. Посмотрите ниже на коэффициенты перевода и вам все станет понятно. Достаточно лишь воспользоваться кнопкой умножения на калькуляторе.
1 м3/час равен 0,278 л/сек
1 л/сек равен 3,600 м3/час
Думаю такая информация будет весь полезна при любых расчётах в гидравлике. Примеры приводить нет смысла, если очень надо то посмотрите калькулятор расчета диаметра трубы по расходу воды, там всё это есть.
Было полезно? Поделитесь с друзьями!
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы,
калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и
криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день.
Информация из официальных источников, постоянное обновление.
Через уравнение.
S — пройденный путь, растояние, которое прошла, например, лодка. (км)
t — время, за которое она прошла расстояние S. (часов, минут)
V — собственная её скорость (км/ч, м/ч)
Такие задачи решаются далее: если известны: (под формулы подставляем числа)
t и V, то перемножаем — t * V, получаем S.
t и S, то расстояние делим время — S : t, получаем V
S и V, также — S : V, получаем t
Также если в задаче указана V (её ищем)
по течению, то V собственная + V по течению
против течения, то V собств. — V прот. теч.
Тогда формулы звучат так: если известны:
t и V, то t * (V с. +/- V) = S
t и S, то S : t = V с. +/- V
V и S, то S : (V c. +/- V) = t
Теперь ещё раз:
V c. — собственная скорость
V c. + V — скорость + скорость по теч.
V c. — V — скорость + скорость прот. теч.
Ну так чтоли… Плохой из меня учитель(((