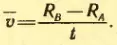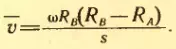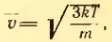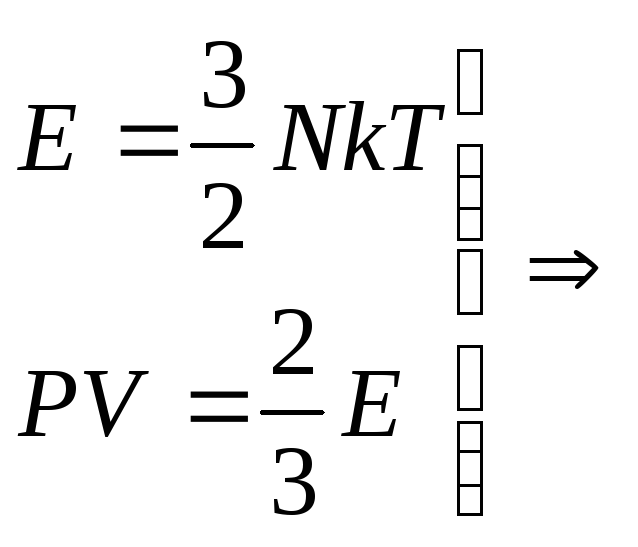Как найти скорость движения молекулы водорода

Условие задачи:

Определить среднюю квадратичную скорость молекул водорода при нормальных условиях.

Задача №4.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(upsilon_{кв}-?)

Решение задачи:

Кинетическую энергию поступательного движения молекул газа можно определять по двум формулам:

[left{ begin{gathered}
{E_к} = frac{{{m_0}upsilon _{кв}^2}}{2} hfill \
{E_к} = frac{3}{2}kT hfill \
end{gathered} right.]

Приравняем эти два выражения и выразим среднюю квадратичную скорость (upsilon_{кв}):

[frac{{{m_0}upsilon _{кв}^2}}{2} = frac{3}{2}kT]

[{upsilon _{кв}} = sqrt {frac{{3kT}}{{{m_0}}}} ;;;;(1)]

Массу одной молекулы (m_0) можно узнать, если разделить молярную массу (M) на число Авогадро (N_А):

[{m_0} = frac{M}{{{N_А}}}]

Молярная масса водорода (H₂) равна 0,002 кг/моль.

В таком случае формула (1) примет такой вид:

[{upsilon _{кв}} = sqrt {frac{{3k{N_А}T}}{M}} ]

Известно, что произведение двух постоянных – постоянной Больцмана (k) и числа Авогадро (N_А) – дают в результате универсальную газовую постоянную (R), равную 8,31 Дж/(моль·К).

Таким образом, получим:

[{upsilon _{кв}} = sqrt {frac{{3RT}}{M}} ]

Нормальным условиям соответствует давление (p), равное (приближенно) атмосферному, то есть 100 кПа, и температура (T), равная 0° C или 273 К.

Считаем ответ:

[{upsilon _{кв}} = sqrt {frac{{3 cdot 8,31 cdot 273}}{{0,002}}}  = 1844,7;м/с approx 1,8;км/с]

Ответ: 1,8 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.21 В сосуде находится газ под давлением 150 кПа при температуре 23 C. Найти
4.1.23 Под каким давлением находится кислород в баллоне, если при температуре 27 C
4.1.24 При какой температуре средняя квадратичная скорость молекул кислорода

Средняя скорость теплового движения молекул. Уравнение (2.9) дает возможность найти среднюю скорость теплового движения молекул. Подставляя в это уравнение 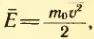получим выражение для среднего квадрата скорости:

     (2.11)

Отсюда средняя скорость молекулы (точнее, средняя квадратическая скорость) равна:

     (2.12)

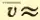
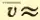
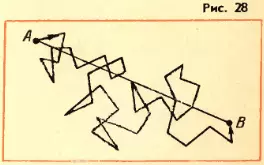
Вычисляя по формуле (2.12) скорость молекул, например азота, при t = 0°C, получим: 500 м/с. Молекулы водорода при той же температуре имеют скорость 1800 м/с.
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчетам оказались большими, чем скорости артиллерийских снарядов! Высказывали на этом основании даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла. Это нетрудно объяснить. Из-за столкновений молекул траектория каждой молекулы представляет собой запутанную ломаную линию (рис. 28). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком либо направлении в среднем невелико даже за время нарядна нескольких минут. При перемещении молекулы из точки A в точку B пройденный ею путь оказывается гораздо больше расстояния |AB|.

Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (2.12). Один из опытов был предложен Штерном в 1920 г.

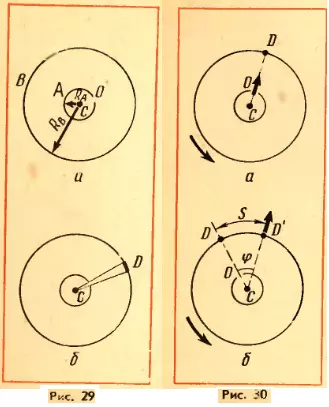
Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жестко связанных друг с другом (рис. 29, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка C, покрытая слоем серебра. По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель O. Воздух из цилиндров откачан. Цилиндр B находится при комнатной температуре.

Вначале прибор неподвижен. При прохождении тока по нити слой серебра испаряется и внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель O и, достигнув внутренней поверхности цилиндра B, осаждаются на ней. В результате прямо против щели образуется узкая полоска серебра D (рис. 29, б).

Затем цилиндры приводит во вращение с угловой скоростью ω. Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров R_B — R_A, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадут на внутреннюю поверхность большого цилиндра не прямо против щели O (рис. 30, а), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 30, б). Ведь атомы движутся прямолинейно. Расстояние s равно:

s = φ R_B = ωtR_B     (2.13)

В действительности не все атомы серебра имеют одну и ту же скорость. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полоскал D и D’ с наибольшей концентрацией атомов серебра. Этому расстоянию будет соответствовать средняя скорость атомов.

Средняя скорость атома равна:

Подставляя в эту формулу значение t из выражения (2.13), получим:

Зная ω, R_A и R_B и измеряя среднее смещение s полоски серебра, вызванное вращением прибора, находим среднюю скорость атомов серебра.

Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратической скорости. Это служит экспериментальным доказательством справедливости формулы (2.12), а следовательно и (2.9), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.

Средняя скорость броуновской частицы. Формула (2.12) позволяет понять почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица, участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (2.9), а средняя квадратическая скорость — формулой

где m — масса броуновской частицы. Если масса частицы велике, то средняя скорость ее движения настолько мала, что движение частицы практически нельзя обнаружить.

1. Как изменится средняя квадратическая скорость движения молекул при увеличении температуры в 4 раза? 2. Какие молекулы в атмосфере движутся быстрее: молекулы азота или молекулы кислорода? 3. Почему толщина слоя полоски серебра на поверхности внешнего вращающегося цилиндра в опыте Штерна неодинакова по ширине полоски?

Квадрат средней квадратичной скорости вычисляется по формуле:

² = 3·R·T / M

Дано:

R = 8,31 Дж/(К·моль) — универсальная газовая постоянная

t =  27°C     T = 27 + 273 = 300 К — температура в градуса Кельвина

M = 0,002 кг/моль — молярная масса водорода

² = 3·8,31·300 / 0,002 ≈ 3 740 000 (м/с)²

Тогда:

= √(3 740 000) ≈ 1930 м/с ≈ 1,93 км/с

Ответ Скорость молекулы водорода очень большая — почти 2 километра в секунду!

Так как
,
то, следовательно,
…(11.12)

где
–
кинетическая энергия всех молекул газа.

Массу газа можно
выразить как
,
тогда (12.12) запишется как
;
для одного моля газа, то есть m
= M, а V = V_


,
отсюда

Так как молярную
массу можно выразить через массу одной
молекулы m₀
и число Авогадро —
,
то квадратичную скорость можно представить
как

где

— постоянная Больцмана.

При комнатной
температуре молекулы кислорода, например,
имеют среднеквадратическую скорость
480м/с, водорода – 1900м/с.

6. Средняя кинетическая энергия поступательного движения молекул газа.

Средняя кинетическая
энергия поступательного движения одной
молекулы идеального газа

– она пропорциональна термодина-мической
температуре и зависит только от нее, то
есть
температура тела есть количественная
мера энергии движения молекул, из которых
состоит это тело. Кроме
того, связи между абсолютной температурой
и средней кинетической энергией
показывает, что при
одинаковой температуре средние
кинетические энергии молекул всех газов
одинаковы, несмотря на различие масс
молекул разных газов.

Кинетическая
энергия газа состоящего из

молекул, равна

,
то есть
,
отсюда
,
где

— концентрация молекул, тогда

– получили уравнение состояния идеального
газа. Из этих выражений видно, что если

то <E₀>
= 0, то есть прекращается поступательное
движение молекул идеального газа, а, ,
его давление равно нулю.

Не следует думать,
что при абсолютном нуле температуры,
прекращается всякое движение частиц
вещества. Даже если все молекулы газа
остановятся, то внутри них будут двигаться
электроны, будут участвовать в движении
протоны и нейтроны ядер.

Абсолютный ноль
температур означает для реальной системы
не отсутствие движения, но такое состояние
тела, при котором дальнейшее уменьшение
интенсивности этого движения за счет
отдачи его энергии окружающим телам
невозможно. Следовательно, при абсолютном
нуле система находится в состоянии с
наименьшей возможной энергией.
Характер этого состояния зависит от
конкретных свойств составляющих систему
частиц.

7. Любая
молекулярная система состоит из большого
числа составных частиц (идеальный газ).
Эти частицы беспорядочно движутся.
Скорости каждой частицы в произвольный
момент времени неизвестны. Но, оказываются
разные
скорости различных частиц встречаются
с разными вероятностями.
В этом можно убедится на опыте Штерна
(1888 – 1970):

поверхности
внешнего цилиндра, они создают изображение
щели, которое можно увидеть, если через
некоторое время развернуть внутреннюю
поверхность большого цилиндра. Если
прибор привести во вращение вокруг
общей оси, то атомы серебра, прошедшие
сквозь щель, будут оседать не прямо
напротив него, а с некоторым смещением.
Если бы всех молекул серебра была
одинакова, то и это смещение было бы
одинаковым, но опыт показал распределение
по скоростям.

Чем больше скорость
частиц отличается от U_в,
тем меньше число таких частиц. С
увеличением

возрастает наиболее вероятная скорость,
больше появится быстрых частиц, вся
кривая сместится вправо. Однако площадь
под кривой остается постоянной (так как
постоянно число частиц), кривая
растягивается. Сама кривая называется:
распределение
Максвелла молекул по скоростям.

Применив методы
теории вероятностей, Максвелл нашел
функцию распределения по скоростям
f
(1)

Значение наиболее
вероятной скорости можно найти,
продифференцировав (1):

(2)

Средняя скорость
молекул определяется по формуле:

(3)

Таким образом,
состояние газа характеризуется следующими
скоростями:

1) наиболее вероятная

2) средняя

3) Средняя квадратичная

Исходя из
распределения молекул по скоростям
можно определить функцию
распределения молекул по энергиям
теплового движения

(4)

Тогда средняя
кинетическая энергия :

7

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!