Как найти сколько соли в растворе

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.

• 9%-я концентрация раствора соли — это 9 грамм соли в
  100 граммах раствора.

Разбор примера

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.

Ответ: 10% — концентрация раствора.

Разбор примера

Теперь решим обратную задачу.

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.

Сложная задача на растворы

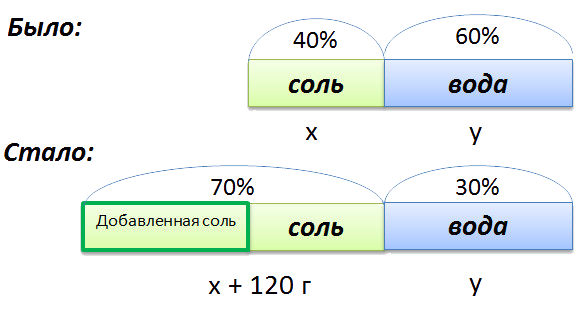
В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет

100% − 40%= 60%

Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.

Этой величиной является масса воды в растворе «y».

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г — масса соли в новом растворе
• (100% − 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.

Ответ: 48 г — масса соли в первоначальном растворе.

Ваши комментарии

Оставить комментарий:

Формула концентрации раствора. Их множество. И каждая соответствует тому или иному способу выражения концентрации. А в химии их применяются достаточно: массовая доля растворенного вещества, молярная, нормальная, моляльная, титр и др.

Зачем так много? Ответ на этот вопрос очень прост. Каждый вид концентрации удобен в том или ином  случае, когда применение другого вида концентрации неуместно.

Например, при исследовании содержания массы вещества в очень небольшом объеме раствора удобно пользоваться титром. А в каких-то технологиях вообще концентрация заменяется другими количественными характеристиками раствора. Так, в технологии посола рыбы для расчета необходимой концентрации тузлука (раствора поваренной соли) используют не его процентную концентрацию, а плотность.

Содержание:

1. Концентрация – что это такое

2. Формула концентрации раствора: основные виды

3. Массовая доля растворенного вещества и примеры ее вычисления

• разбавление раствора водой
• концентрирование раствора путем упаривания
• концентрирование раствора путем добавления растворенного вещества
• смешивание двух растворов
• применение кристаллогидратов для приготовления раствора (задачи на кристаллогидраты)

4. Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов

Концентрация – что это такое

Любой раствор имеет различные характеристики: качественные и количественные. Одной из важнейших количественных характеристик является концентрация раствора.

Концентрация раствора – это количество растворенного вещества, содержащееся в определенном количестве раствора.

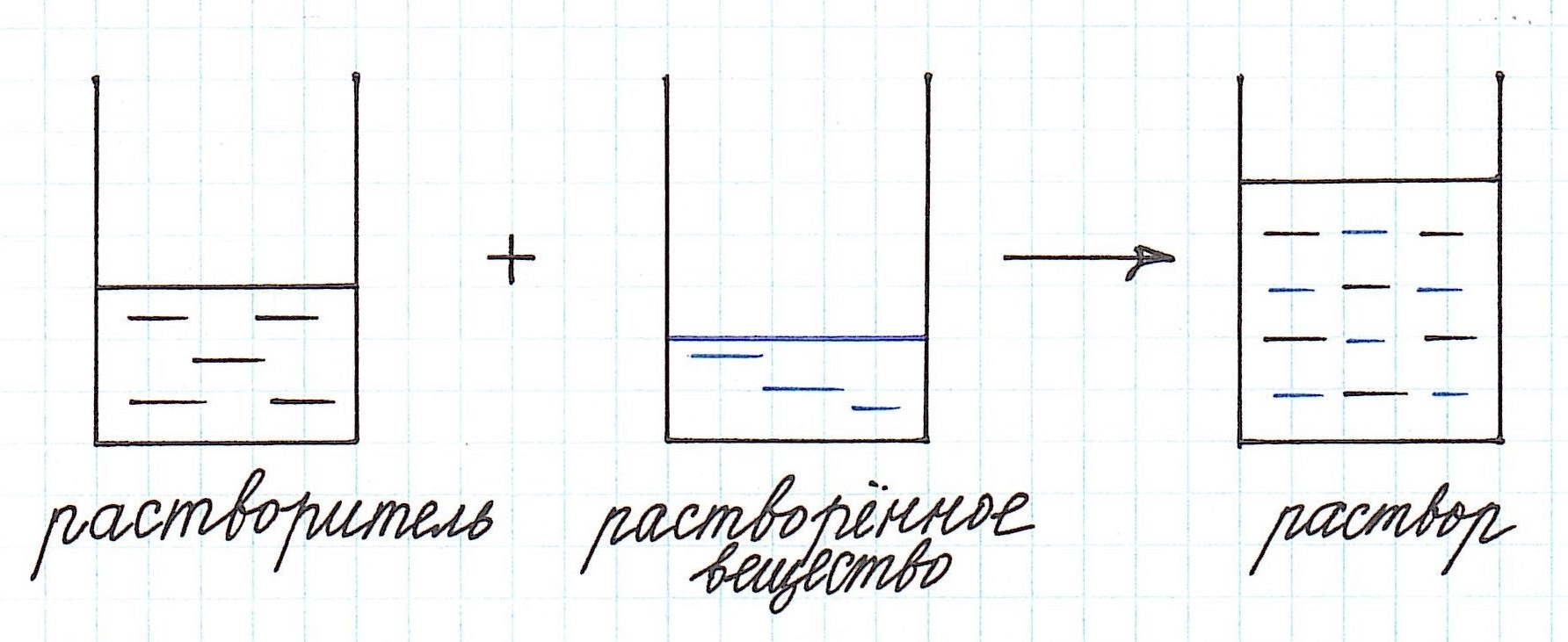
Как видно из приведенного определения, основными компонентами раствора являются:

— растворитель;

— растворенное вещество.

Растворенного вещества в растворе всегда меньше, а растворителя больше.

И вот именно с вычислением количественного содержания растворенного вещества чаще всего и связаны все расчеты, основанные на применении формулы концентрации раствора.

Существует несколько видов концентрации раствора:

— массовая доля растворенного вещества;

— объемная доля растворенного вещества;

— молярная доля растворенного вещества;

— молярная (или молярность);

— моляльная (или моляльность);

— нормальная (или эквивалентная);

— титр.

 Формула концентрации раствора: основные виды

Применение того или иного вида концентрации уместно в каждом конкретном случае. Не существует какой-то универсальной концентрации или универсальной формулы концентрации раствора.

Кстати, с помощью математических преобразований можно перейти от одной концентрации к другой или найти взаимосвязь между разными их видами.

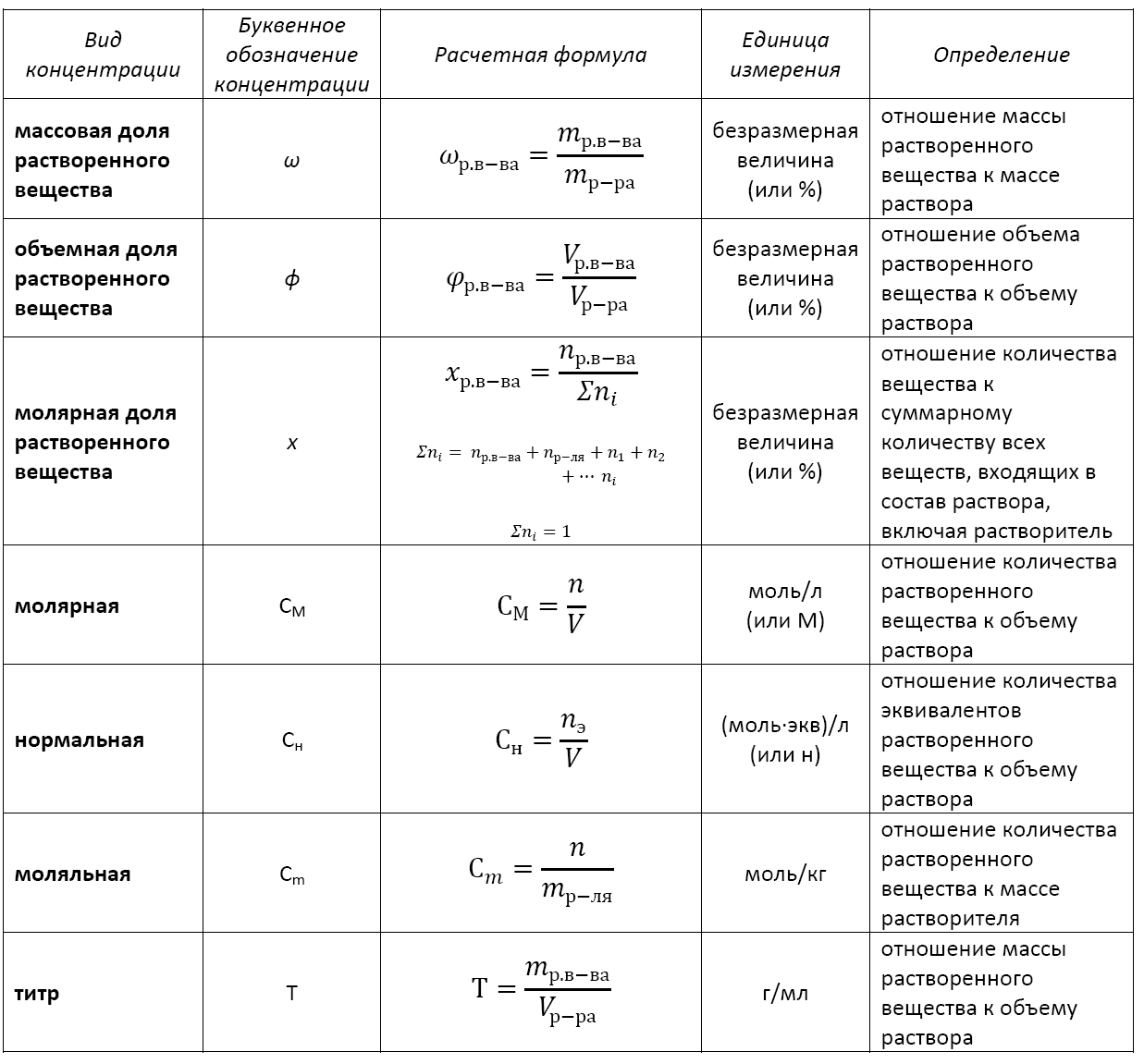
Основные расчетные формулы концентрации раствора приведены в таблице:

Массовая доля растворенного вещества и примеры ее вычисления

Массовая доля растворенного вещества – это отношение массы растворенного вещества к массе раствора.

Ее расчетная формула выглядит так:

где ω_р.в-ва – массовая доля растворенного вещества, m_р.в-ва – масса растворенного вещества, m_р-ра – масса раствора.

ω_р.в-ва  представляет собой долю или от единицы или от 100%.  Так, например, имеется двухпроцентный раствор NaCl. Его концентрация будет записана в первом случае ω(NaCl) = 0,02, а во втором – ω(NaCl) = 2%. Форма записи основной сути не меняет. Можно записывать и так, и так.

Что же означает выражение ω(NaCl) = 0,02 или ω(NaCl) = 2%? Буквально следующее: в 100 г водного раствора поваренной соли содержится 2 г этой соли и 98 г воды.

Необходимо помнить, что раствор состоит из растворителя и растворенного вещества. Поэтому масса раствора будет состоять из массы растворителя и массы растворенного вещества:

Тогда основную расчетную формулу для массовой доли растворенного вещества можно преобразовать:

Очень часто в расчетах с процентной концентрацией используются плотность и объем раствора:

В таком случае основную расчетную формулу концентрации раствора можно преобразовать и так:

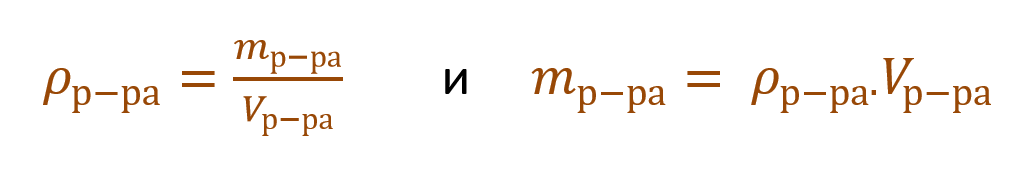
В других ситуациях могут использоваться объем и плотность не раствора, а растворителя. Тогда основная формула для расчета концентрации будет выглядеть так:

На практике бывает необходимо не только приготовить раствор с какой-либо определенной концентрацией, но и увеличить, либо уменьшить ее значение. Это достигается различными приемами:

— упариванием раствора;

— добавлением растворенного вещества;

— добавлением к раствору растворителя (например, воды).

Кроме того, приходится часто смешивать друг с другом растворы разных концентраций.

Разберем все возможные случаи.

Мы рекомендуем задачи, в которых речь идет о растворах, решать с использованием схематических рисунков. Это очень наглядно, особенно, когда речь идет о смешивании растворов.

Начнем с самого простого: вычислим концентрацию раствора.

Пример 1. В 200 г воды растворили 40 г глюкозы. Вычислите массовую долю глюкозы в полученном растворе.

Обратите внимание, что речи о каком-либо химическом взаимодействии не идет! Поэтому записывать уравнения реакций не требуется!

Запишем общую формулу для расчета массовой доли растворенного вещества:

В данной задаче глюкоза (C₆H₁₂O₆) – растворенное вещество, а вода (H₂O) – растворитель. Масса раствора будет складываться из массы глюкозы и массы воды:

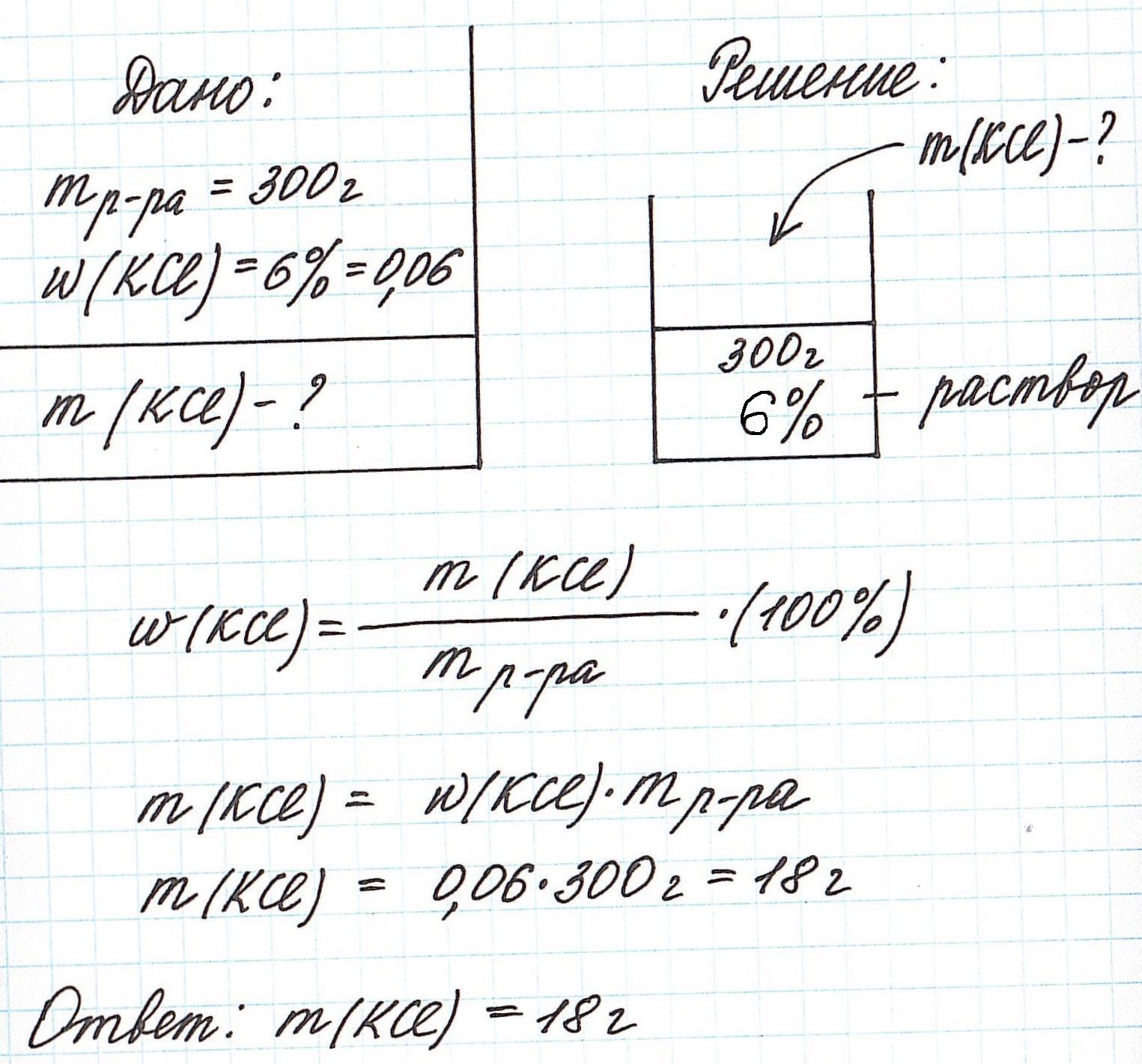
Пример 2. Рассчитайте, сколько потребуется хлорида калия, чтобы приготовить 300 г раствора с массовой долей соли 6%.

Обратите внимание, для того, чтобы расчеты были менее громоздкими, будем использовать выражение концентрации не в %, а в долях от единицы.

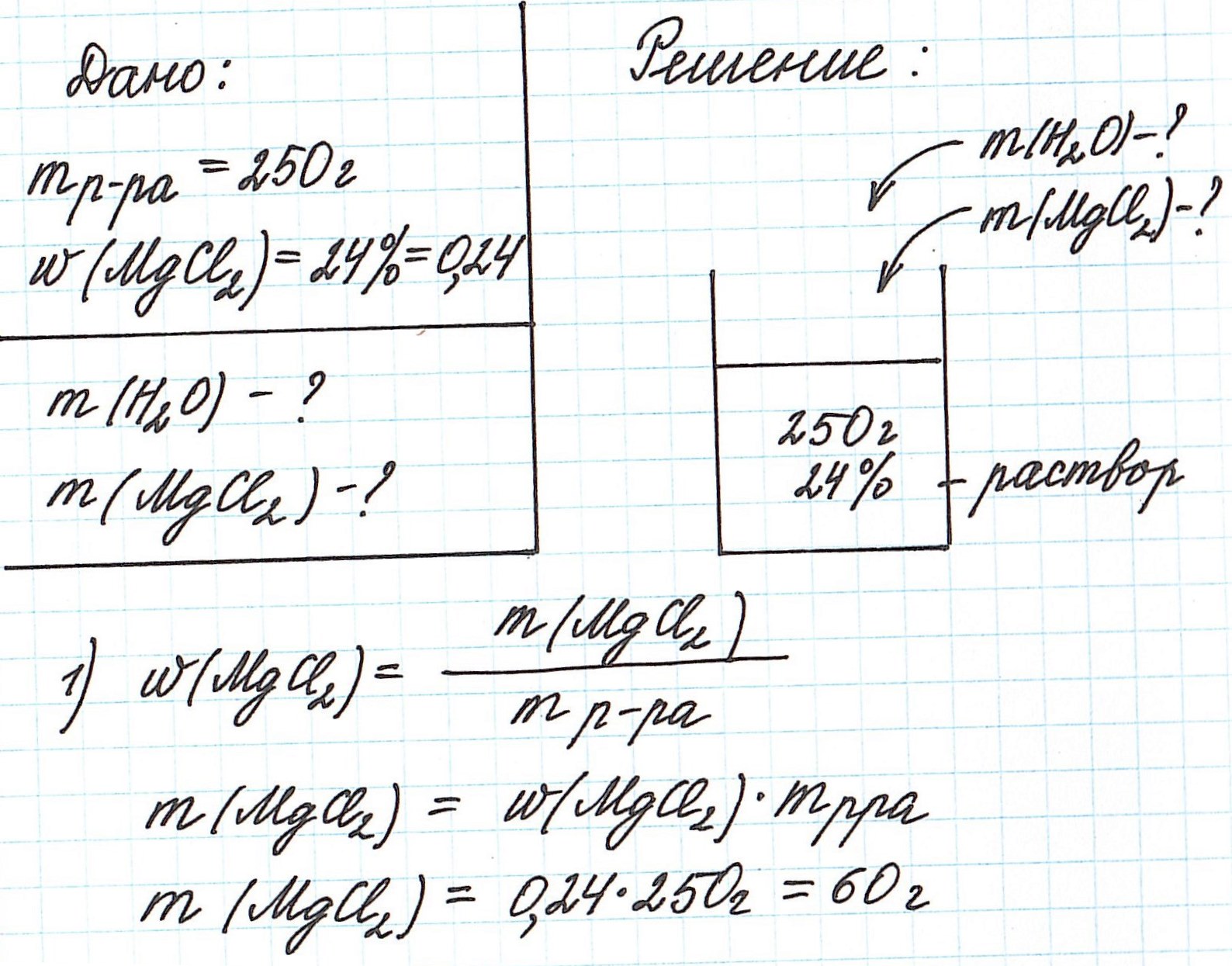
Пример 3.  Необходимо приготовить 250 г раствора с массовой долей хлорида магния 24%. Рассчитайте массу требуемых воды и соли.

Так как раствор готовится из хлорида магния и воды, то и масса раствора равна сумме масс хлорида магния и воды:

Рассмотрим задачу, в которой в качестве растворителя выступает не вода, а другое вещество.

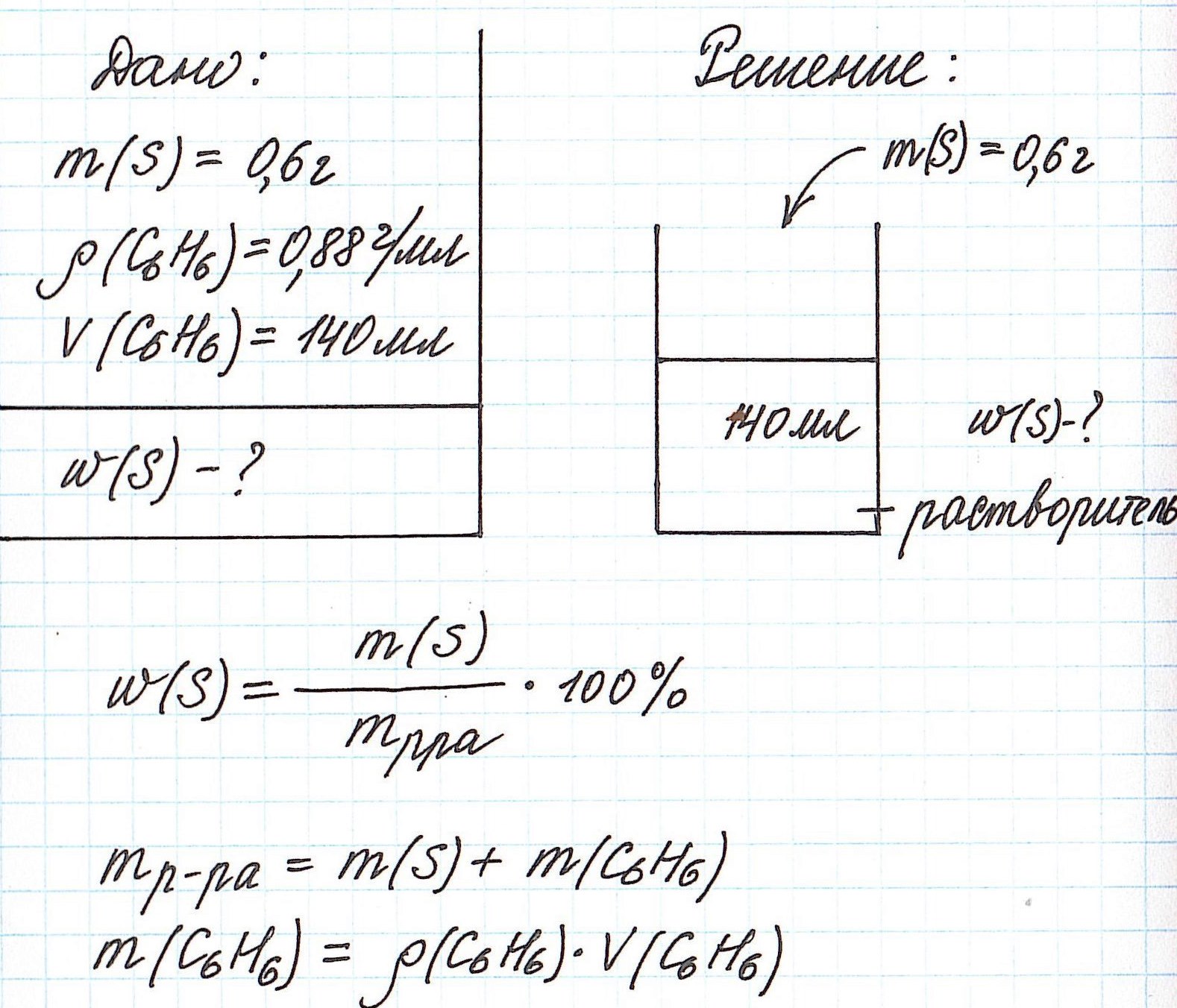
Пример 4.   В органическом растворителе бензоле объемом 140 мл растворили серу массой 0,6 г. Вычислите массовую долю серы в полученном растворе, если плотность бензола составляет 0,88 г/мл.

Обратите внимание, что здесь:

— масса раствора не известна;

— масса растворителя (бензола) не известна;

— известны объем и плотность растворителя (бензола), что позволяет нам найти его массу;

— масса раствора состоит из массы растворителя (бензол) и массы растворенного вещества (сера).

Объединим все расчетные формулы в одну и подставим в нее имеющиеся численные значения:

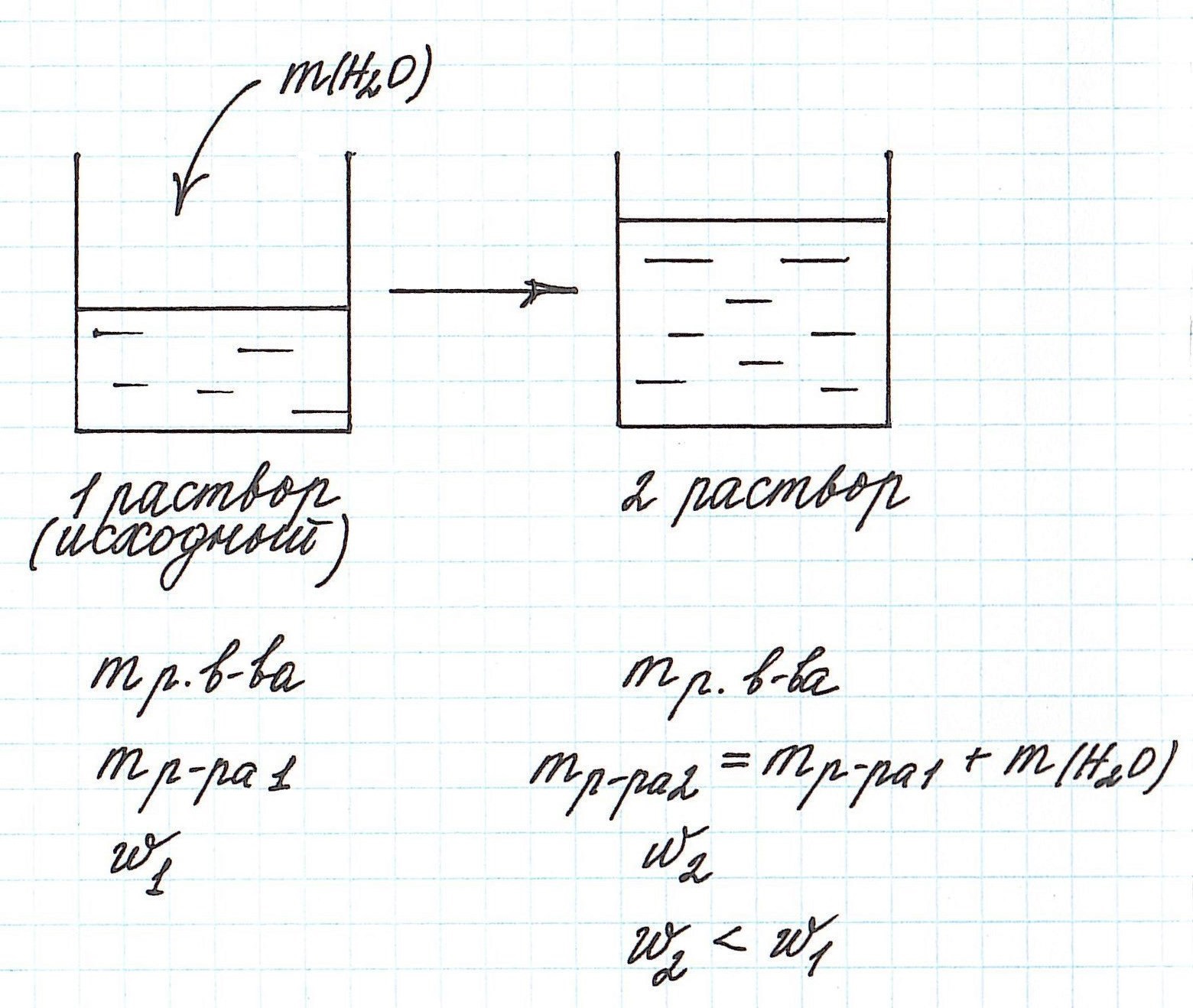
 Вычисление массовой доли растворенного вещества при разбавлении раствора водой

Разбавление раствора водой приводит к уменьшению его концентрации.

Запомним, что в таких случаях:

— увеличивается масса раствора;

— увеличивается масса растворителя;

— масса растворенного вещества остается постоянной.

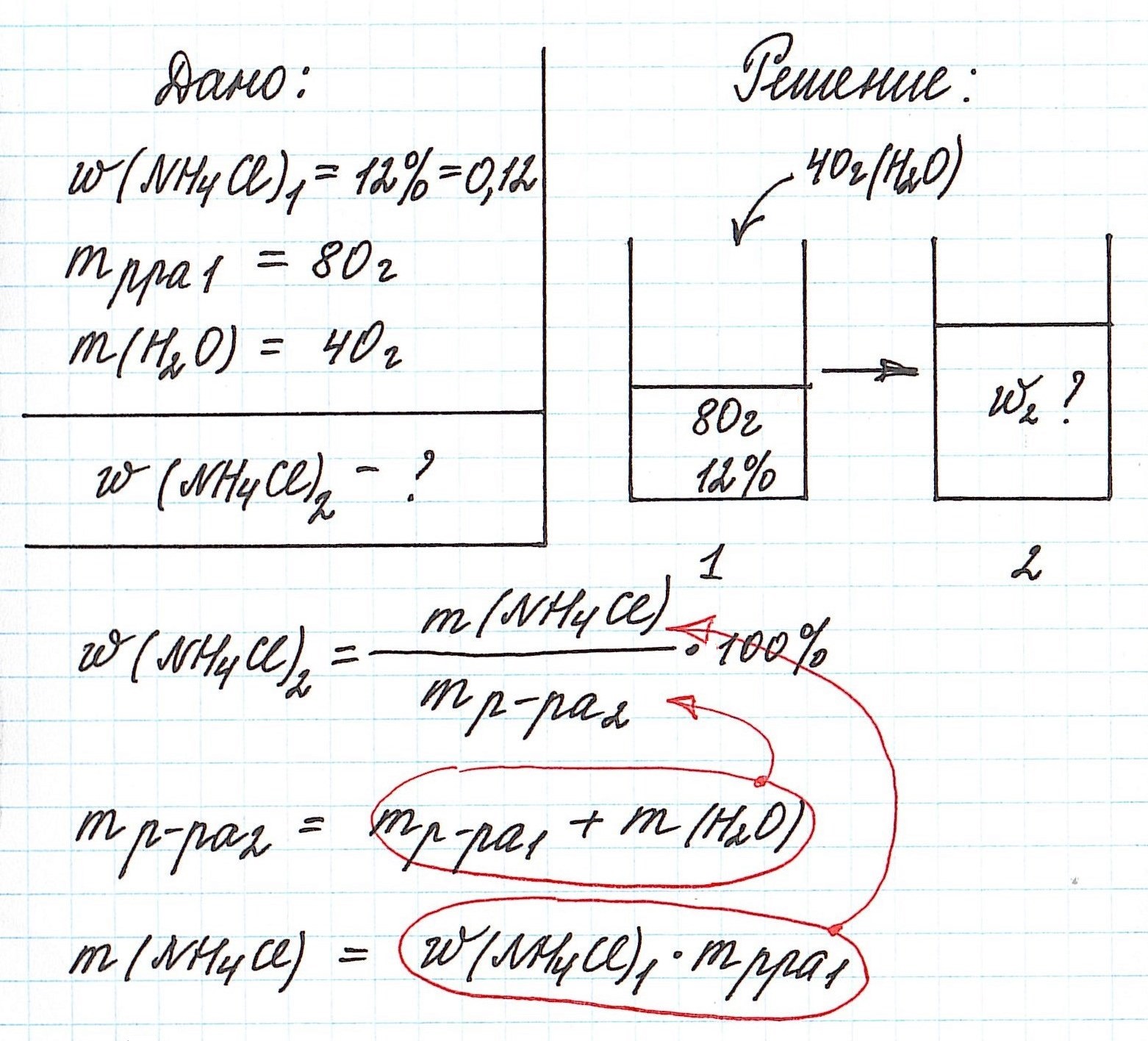
Пример 5.   К 80 г раствора с массовой долей NH₄Cl 12% добавили 40 г воды. Вычислите массовую долю хлорида аммония в полученном растворе.

Объединим все полученные формулы в одну и подставим имеющиеся данные:

Пример 6.   Рассчитайте объем раствора фосфорной кислоты (массовая доля кислоты 12%, плотность 1,065 г/мл), который потребуется для приготовления раствора с массовой долей H₃РO₄ 4% объемом 250 мл (плотность 1,02 г/мл).

В данной задаче речь напрямую о разбавлении раствора не идет. Но судя по тому, что исходный раствор имел концентрацию 12%, а конечный – 4%, становится ясно: последний раствор можно получить путем разбавления первого водой.

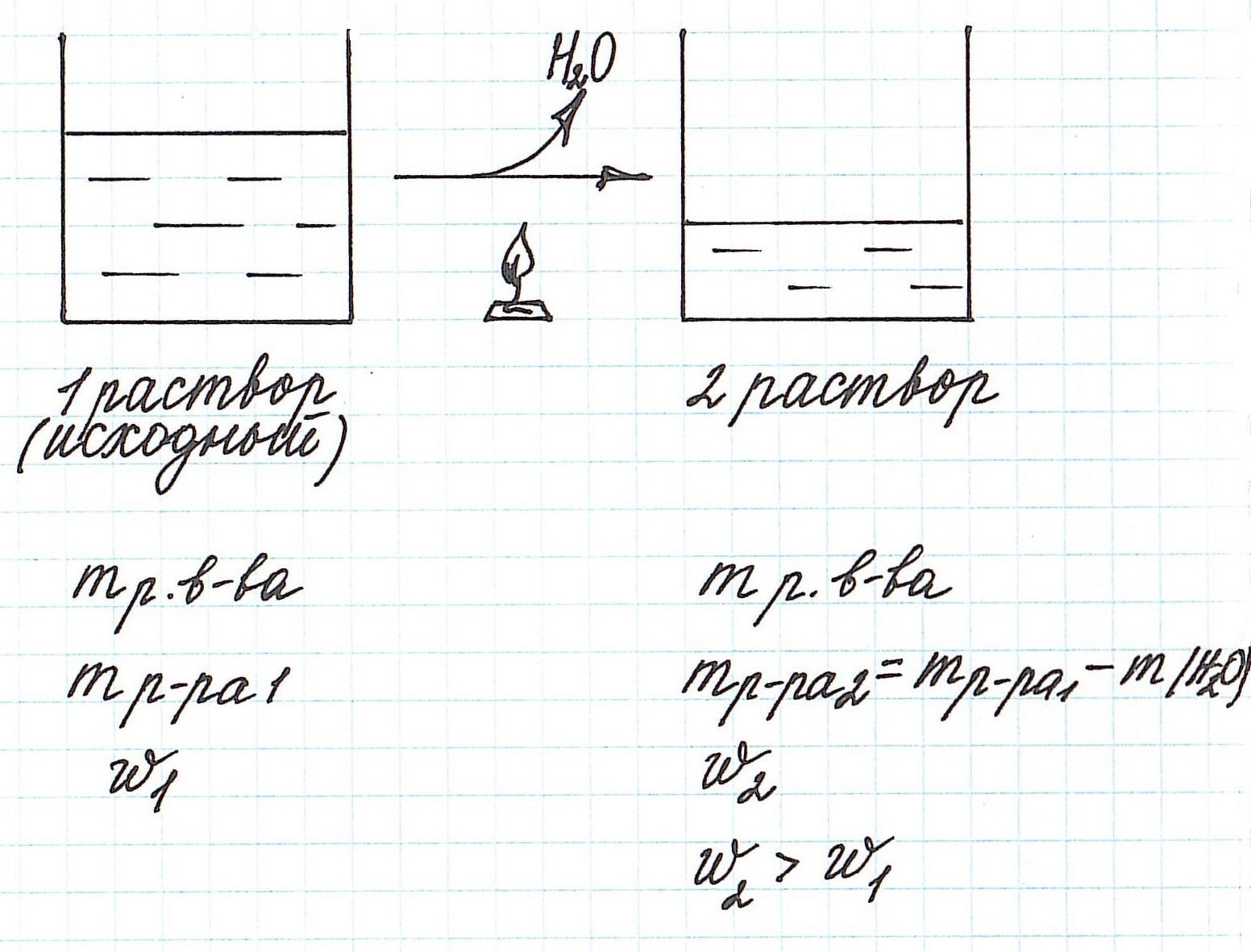
Вычисление массовой доли растворенного вещества при концентрировании раствора путем упаривания

Упаривание раствора, т.е. его нагревание, при котором происходит испарение воды, приводит к увеличению концентрации.

Учтите, что при этом:

— уменьшается масса раствора;

— уменьшается масса растворителя;

— масса растворенного вещества остается постоянной (при условии, что растворенное вещество не разлагается при данной температуре).

Пример 7.    Из 200 г 27%-ного раствора глюкозы выпарили 20 г воды. Определите массовую долю глюкозы в полученном растворе.

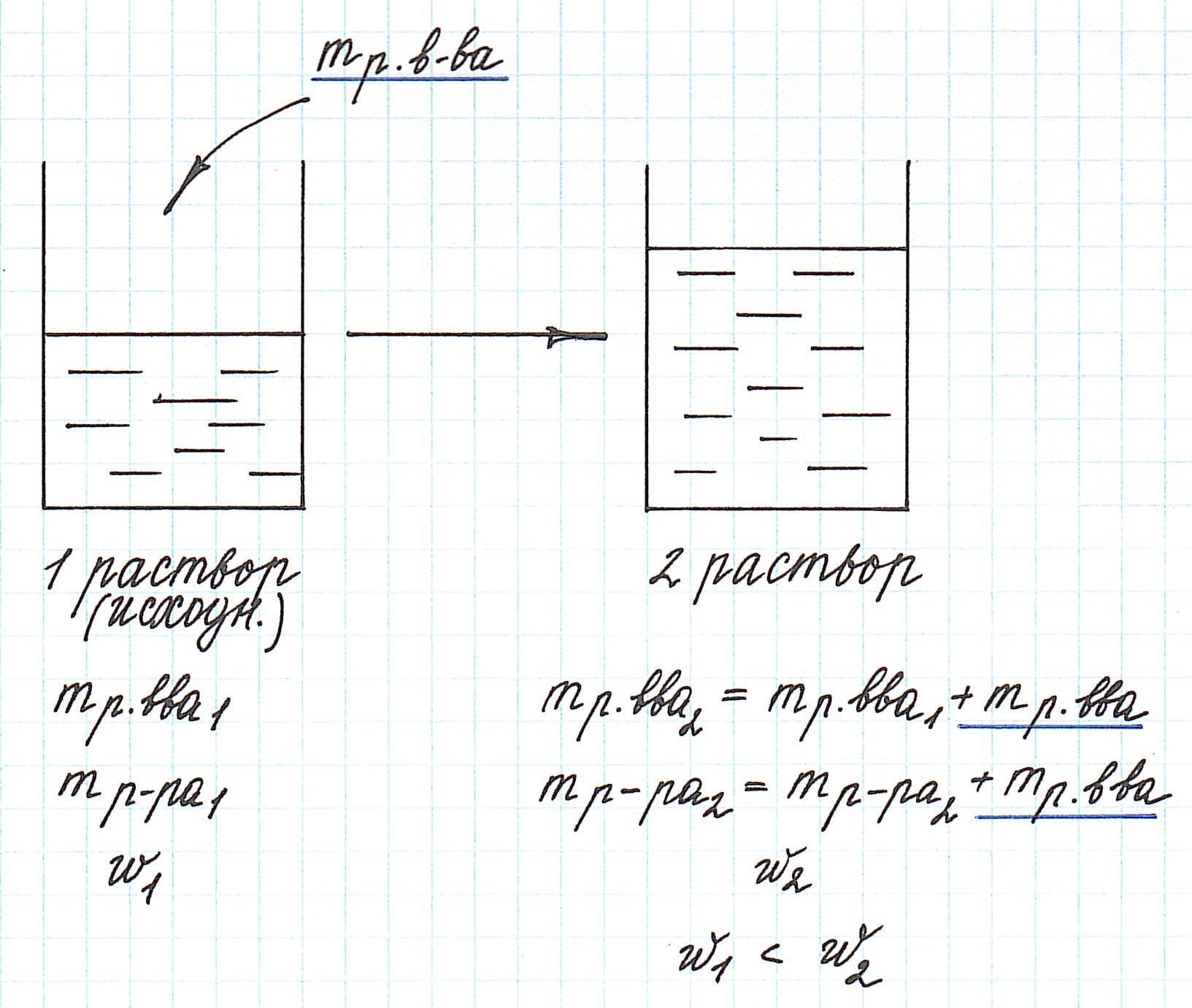
Вычисление массовой доли растворенного вещества при концентрировании раствора путем добавления растворенного вещества

Добавление к уже существующему раствору новой порции растворенного вещества приводит к увеличению концентрации раствора.

Помните, что в таких случаях:

— увеличивается масса раствора;

— увеличивается масса растворенного вещества.

Пример 8.    Определите массу хлорида калия, который надо добавить к 180 г 15%-ного раствора этой соли, чтобы получить 20%-ный раствор.

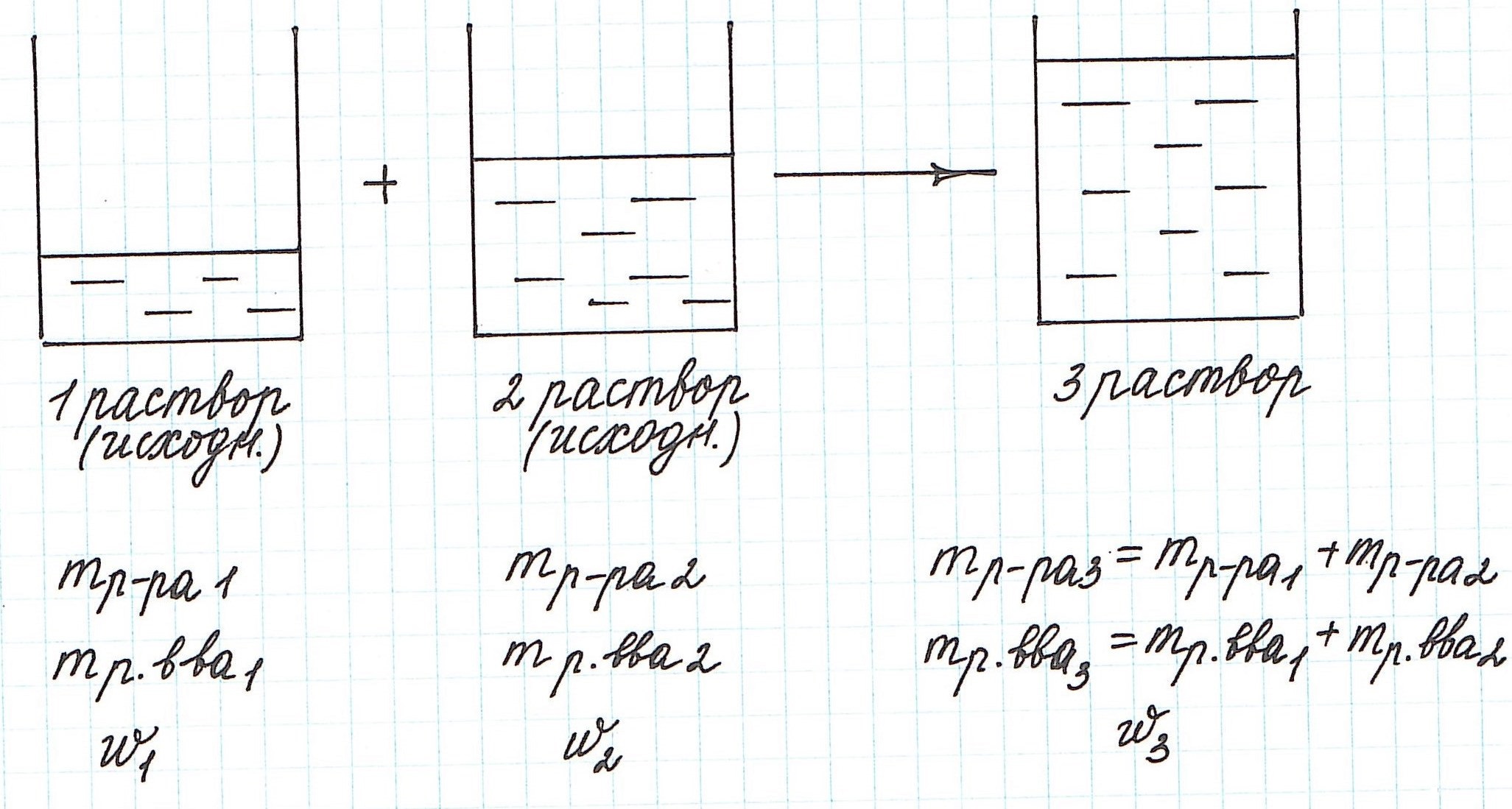
Вычисление массовой доли растворенного вещества при смешивании двух растворов

При смешивании двух растворов (речь о растворах одного и того же вещества конечно же) изменяются все количественные характеристики:

— увеличивается масса раствора;

— увеличивается масса растворенного вещества;

— изменяется массовая доля растворенного вещества.

Пример 9.    Смешали 80 г 32%-ного раствора и 30 г 10%-ного раствора нитрата меди (II). Какова концентрация соли в полученном растворе?

  Вычисление массовой доли растворенного вещества с применением кристаллогидратов для приготовления раствора

Кристаллогидраты используются для приготовления растворов довольно часто. Кристаллогидраты представляют собой вещества, в состав которых помимо основного вещества входят молекулы воды. Например:

CuSO₄·5H₂O – кристаллогидрат сульфата меди (II) (или медный купорос);

Na₂SO₄·10H₂O – кристаллогидрат сульфата натрия (или глауберова соль).

Больше примеров здесь.

Вода, входящая в состав кристаллогидрата, называется кристаллизационной.

Кристаллогидраты различаются прочностью связи между основным веществом и кристаллизационной водой. Одни из них теряют воду при комнатной температуре с течением времени и перестают быть кристаллогидратами (например, Na₂СO₃·10H₂O). Другие – обезвоживаются только при сильном нагревании (например, CuSO₄·5H₂O).

При расчете концентрации с использованием кристаллогидратов для получения растворов часто приходится учитывать и кристаллизационную воду.

Но сначала поясним некоторые нюансы на конкретном примере:

1) Формула CuSO₄·5H₂O означает, что 1 моль CuSO₄·5H₂O содержит 1 моль CuSO₄ и 5 моль H₂O. Это можно было бы записать так:

n(CuSO₄) = n(CuSO₄·5H₂O); n(H₂O) = 5n(CuSO₄·5H₂O)

2) Относительная молекулярная (и численно молярная) масса будет складываться из относительной молекулярной массы вещества и относительной молекулярной массы воды. Например:

Mr(CuSO₄·5H₂O) = Mr(CuSO₄) + 5·Mr(H₂O) = 160 + 5·18 = 250 и, соответственно,

M(CuSO₄·5H₂O) = M(CuSO₄) + 5·M(H₂O) = 160 + 5·18 = 250 г/моль.

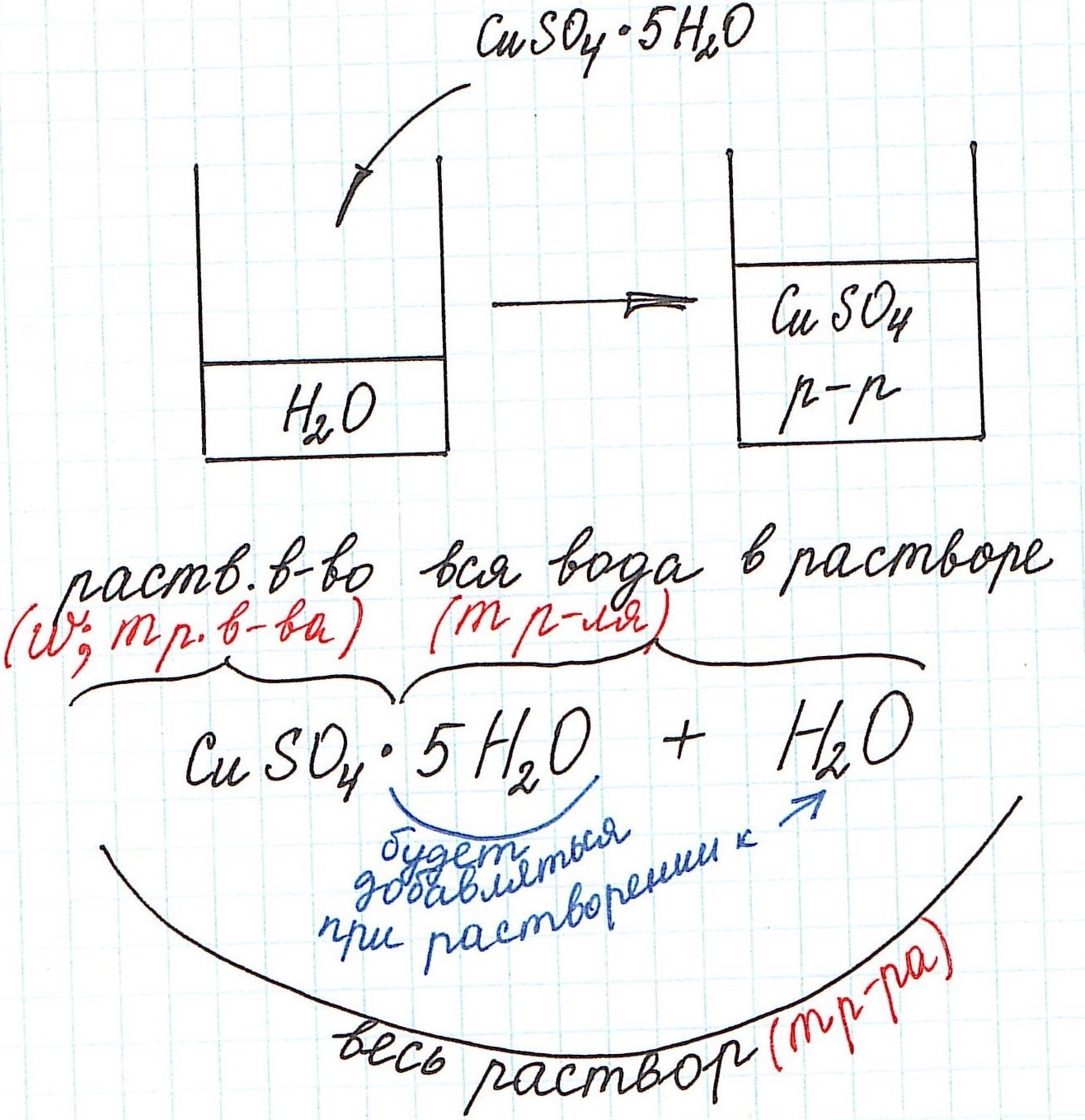
3) Еще одну особенность поясним с помощью рисунка:

Итак, разберем несколько типичных задач.

Пример 10.     В 60 г воды растворили глауберову соль Na₂SO₄·10H₂O массой 5,6 г. Какова массовая доля сульфата натрия в полученном растворе?

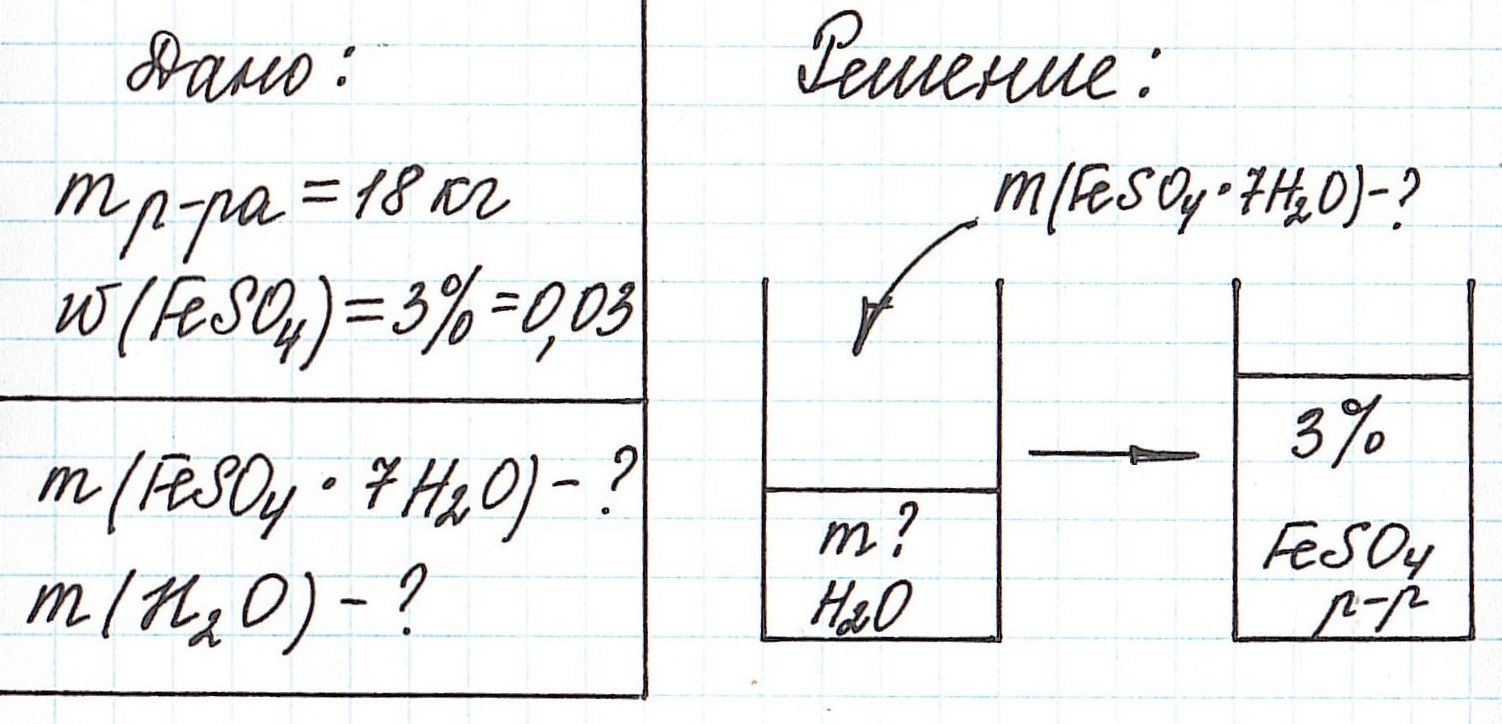
Пример 11.  Какая масса железного купороса FeSO₄·7H₂O и воды потребуется для приготовления 18 кг раствора сульфата железа (II) с массовой долей FeSO₄ 3%?

Обратите внимание, что масса раствора дана не в граммах (г), а в килограммах (кг). Для того, чтобы привести в ходе расчетов все единицы измерения к единой системе, можно перевести килограммы в граммы и вычислять как обычно.

Но есть более простой способ. Можно считать количество вещества не в моль, а в киломоль (кмоль). Молярную массу вычислять не в г/моль, а в кг/кмоль. В этом случае ответ в задаче мы сразу получим в килограммах.

Пример 12. Вычислите массу кристаллогидрата сульфата никеля NiSO₄·7H₂O, который надо добавить к 180 г раствора с массовой долей сульфата никеля 1,5%, чтобы получить раствор с массовой долей соли 6%?

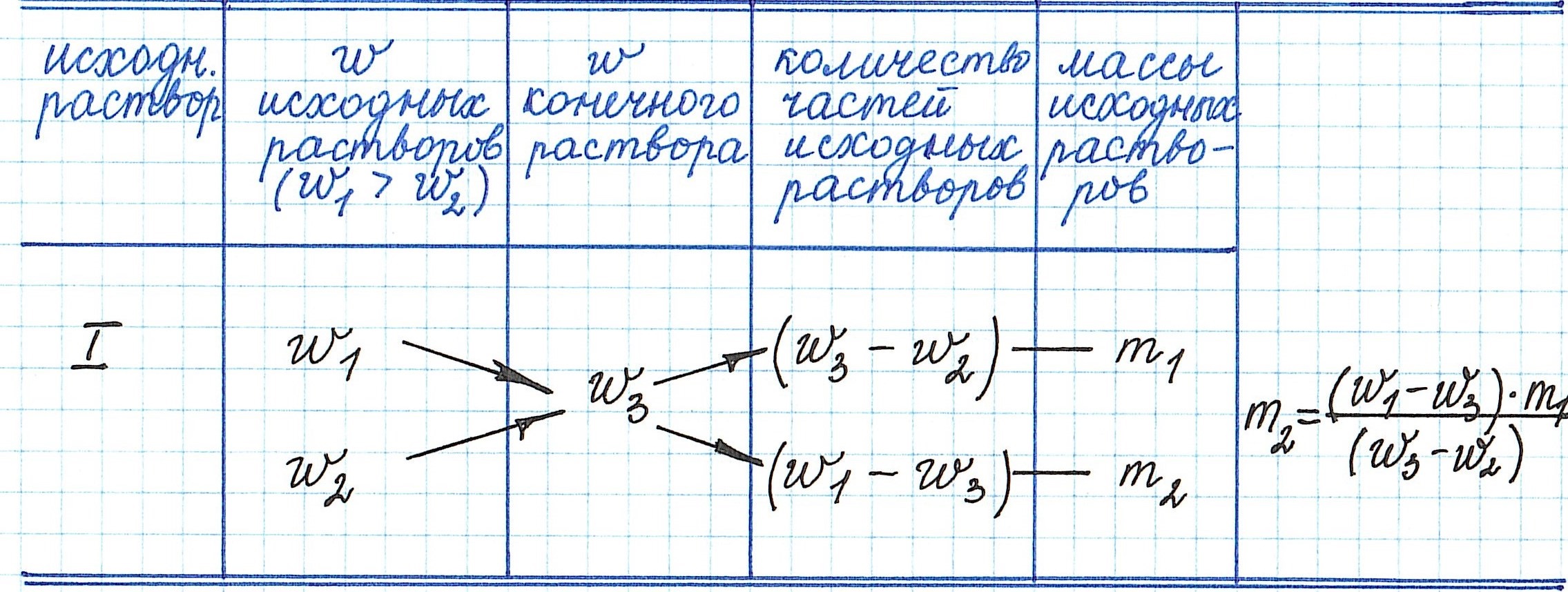
Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов

Правилом «креста» (или «квадратом Пирсона») очень удобно пользоваться в расчетах, связанных с разбавлением или смешиванием растворов.

Общая схема вычислений выглядит так:

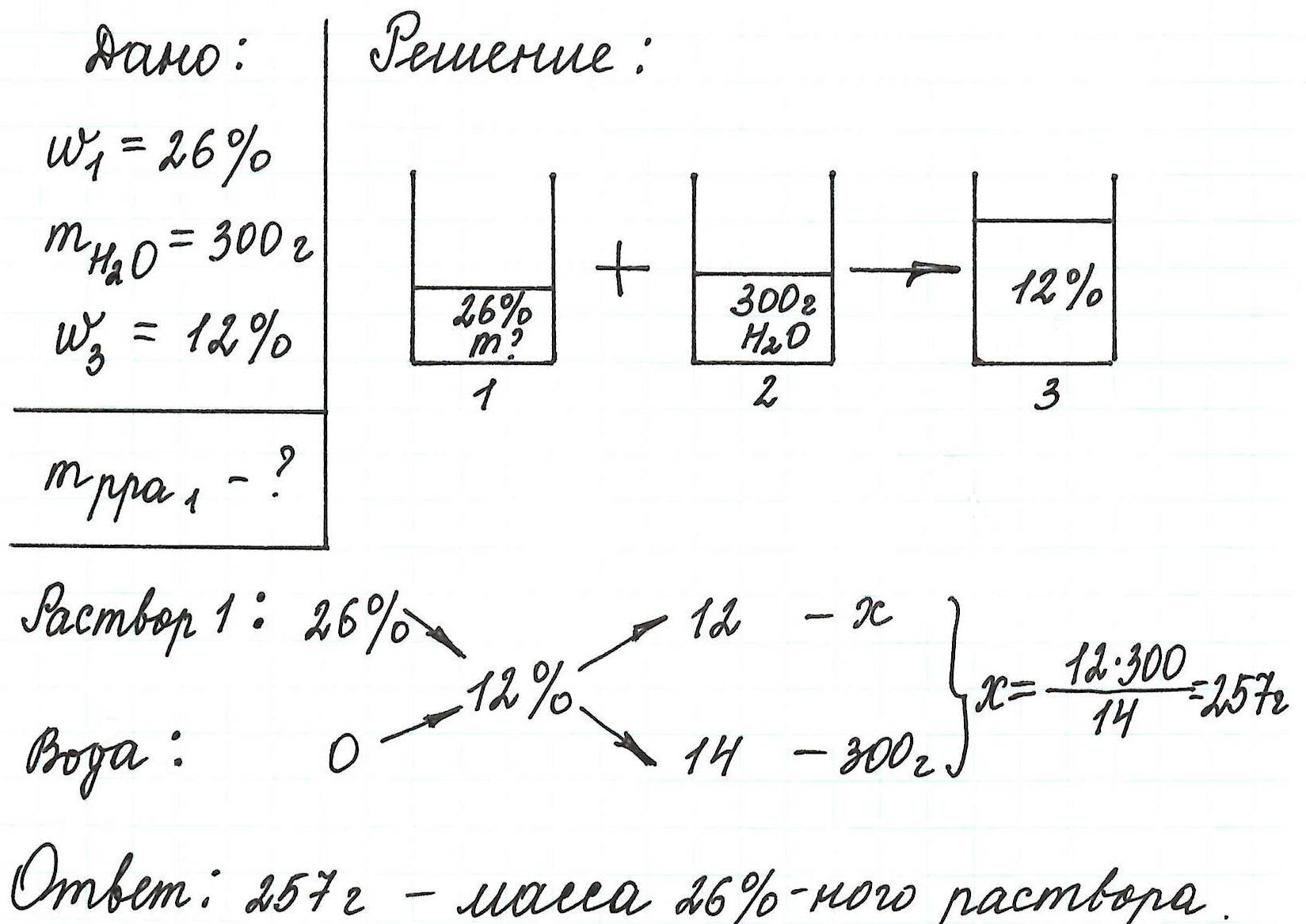
Пример 13. Какую массу 5%-ного раствора глюкозы надо добавить к 70 г 21%-ного раствора этого же вещества, чтобы получить 12%-ный раствор?

Пример 14. Сколько грамм раствора с массовой долей нитрата цинка 26% надо прилить к воде массой 300 г, чтобы получить раствор Zn(NO₃)₂ 12%?

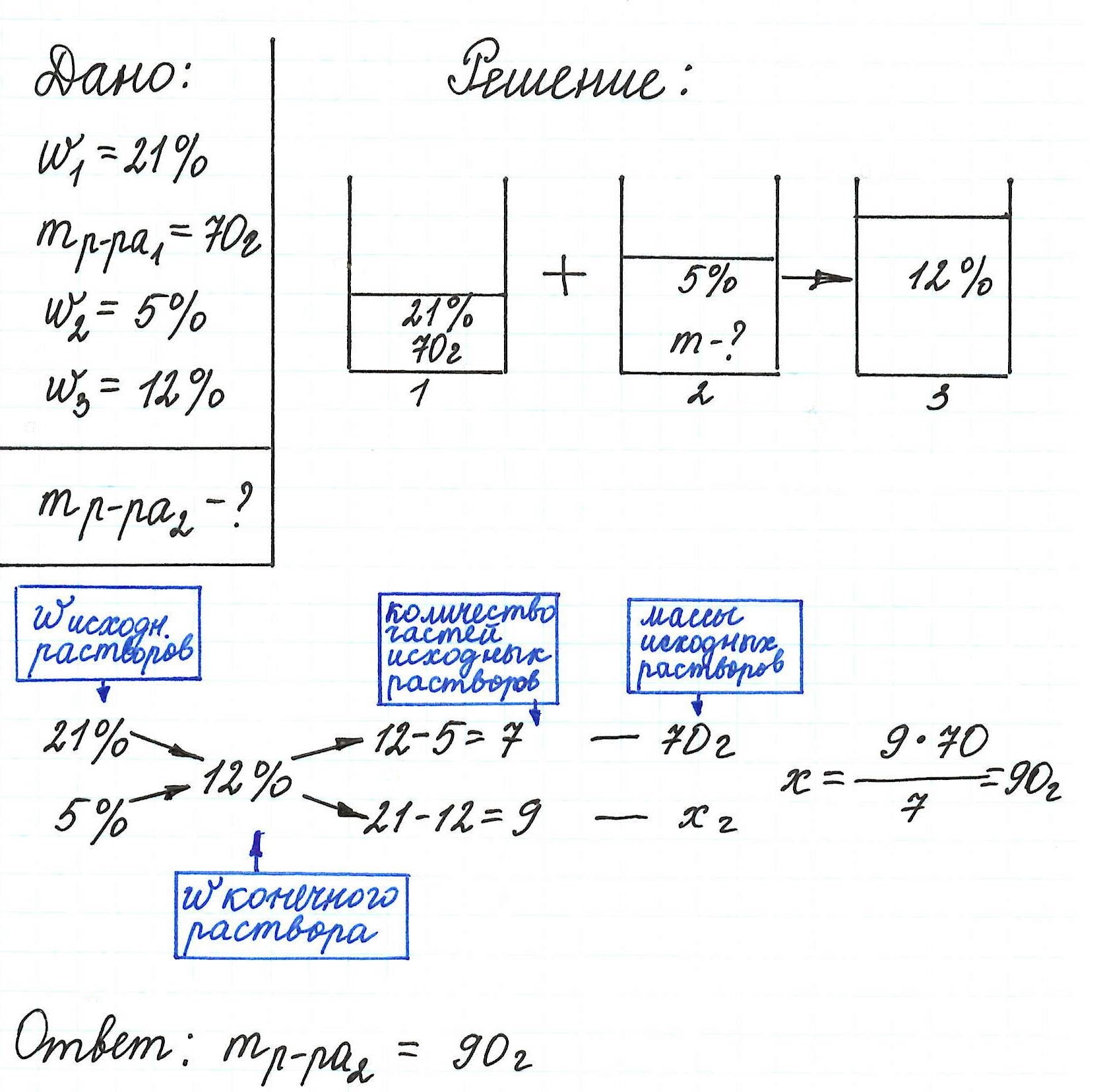
Еще примеры с применением правила «креста» можно посмотреть здесь. 

Мы рассмотрели достаточно примеров расчетов, где используется формула такой концентрации раствора как массовая доля растворенного вещества. Как видим, ситуаций, в которых требуется ее применение, множество. Однако, есть достаточно случаев, когда более приемлемыми являются формулы других концентраций (молярной, нормальной, титра и т.д.). Об этом читайте в других статьях.

Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь к нашей группе ВКонтакте.

или на Одноклассниках

Пожалуйста, оцените публикацию. Большая просьба, если вы оцениваете публикацию от 1 до 3 звезд, обязательно оставьте свой комментарий с указанием того, что не так с этой публикацией. Мы постараемся устранить недостатки.

Ваше мнение для нас важно!

При работе с раствором важно знать, сколько растворённого вещества в нём содержится. Количество растворённого вещества, содержащееся в данном количестве раствора или растворителя, называют его концентрацией. Существует несколько способов выражения концентрации растворов. Рассмотрим простейший из них.

Часто концентрацию выражают в процентах. Процентная концентрация показывает, сколько граммов вещества содержится в 100 г раствора. Например, 3%-й раствор соли — это раствор, в 100 г которого содержится 3 г соли. Масса воды в этом растворе составляет: 100 г – 3 г = 97 г. Для приготовления 100 г этого раствора следует растворить 3 г соли в 97 г воды.

Вычисляя процентную концентрацию, по сути, мы находим массовую долю растворённого вещества (w). Доля, как вы знаете, это часть от целого. Если яблоко разрезали на три равные части и вам досталась одна из них, то ваша доля яблока равна (одна часть из трёх). Массовая доля вещества в растворе — это отношение массы растворённого вещества к общей массе раствора. Массовую долю можно рассчитать по формуле:

Если эту дробь умножить на 100%, то получим значение массовой доли вещества в процентах:

Зная массу раствора и массовую долю растворённого вещества, можно найти массу вещества:

m(вещества) = w(вещества)•m(раствора).

Задача 1. В 380 г воды растворили 20 г иодида калия. Определите массовую долю вещества в полученном растворе.

Массовую долю соли в растворе можно найти двумя способами.

Способ I

w(KI) = ; w(KI) = = 0,05 (5%-й раствор).

Способ II

Учитывая, что числовое значение (в %) массовой доли показывает, сколько граммов вещества содержится в 100 г раствора, составим пропорцию:

в 400 г раствора содержится 20 г KI,

в 100 г раствора — x г KI;

x = = 5 г. Значит, w(KI) = 5%.

О т в е т. w(KI) = 0,05 (5%).

Задача 2. Сколько граммов хлорида натрия и воды необходимо взять для приготовления 250 г 10%-го раствора?

m(NaCl) = 0,1•250 г = 25 г.

m(H₂O) = m(р-ра) – m(NaCl);

m(H₂O) = 250 г – 25 г = 225 г.

Способ II

Учитывая, что 10%-й раствор — это раствор, в 100 г которого содержится 10 г хлорида натрия, составим пропорцию:

в 100 г раствора содержится 10 г NaCl;

в 250 г раствора — x г NaCl,

x = = 25 г.

Рассчитаем массу воды:

m(H₂O) = 250 г – 25 г = 225 г.

О т в е т. m(NaCl) = 25 г; m(H₂O) = 225 г.

Задача 3. Определите массу хлорида натрия, который надо растворить в 200 г воды, чтобы получить 5%-й раствор.

Массовая доля хлорида натрия равна:

w(NaCl) = ;

0,05 = ,

решив уравнение, получим x = 10,5 г.

Способ II

В полученном растворе содержится 95% воды (её масса 200 г) и 5% хлорида натрия, массу которого можно найти по пропорции:

200 г H₂O составляют 95%,

x г NaCl составляют 5%.

Отсюда x = = 10,5 г.

О т в е т. m(NaCl) = 10,5 г.

1.Что называют концентрацией раствора; массовой долей растворённого вещества?

2.Изменится ли концентрация раствора хлорида натрия при его хранении: а) в закрытом сосуде; б) в открытом сосуде?

3.В 120 г раствора содержится 3 г глюкозы. Определите массовую долю растворённого вещества.

4.Сколько граммов хлорида калия образуется при выпаривании 150 г 5%-го раствора?

5.В 180 г воды растворили 20 г соды. Определите массовую долю растворённого вещества.

6.В одном стакане воды (200 г) растворили 0,12 г цианида калия. Определите массовую долю растворённого вещества.

7.Определите массовую долю (в %) сахара в чае, в одном стакане которого (200 г) содержатся две чайные ложки сахарного песка (масса одной чайной ложки сахара составляет 4,6 г).

8.Рассчитайте массу поваренной соли, которую надо взять для приготовления 250 г 5%-го раствора.

9.Сколько граммов сахара и воды необходимо для приготовления 500 г 3%-го раствора сахара?

10.Сколько граммов калийной селитры и воды необходимо для приготовления 3 кг 20%-го раствора?

11.Рассчитайте массовую долю нитрата калия в растворе, полученном при смешении 300 г 5%-го и 200 г 30%-го растворов этого вещества.

12.К 100 г 18%-го раствора хлорида натрия добавили 10 г соли. Рассчитайте массовую долю (в %) соли в полученном растворе.

* 13.Физиологический раствор, который используют в медицине, представляет собой 0,9%-й раствор хлорида натрия. Сколько граммов воды надо добавить к 100 г 12%-го раствора хлорида натрия для получения физиологического раствора?

* 14.Воду насытили на холоде углекислым газом, а затем нагрели до кипения. Как изменится концентрация раствора? Будет ли при нагревании меняться концентрация раствора, если вместо углекислого газа взять калийную селитру; гипс? Воспользуйтесь кривыми растворимости этих веществ.

ПОДГОТОВКА К ЭКЗАМЕНУ

«Вычисление массы растворенного вещества, содержащегося в определенной массе раствора с известной массовой долей»

Алгоритмы решения задач:

Пример 1. Вычисление массовой доли растворенного вещества

Определите массовую долю нитрата калия в растворе, полученном растворением 50 г нитрата калия в 200 г воды.

Пример 2. Вычисление массы растворенного вещества

Вычислите массу гидроксида калия в растворе объемом 600 мл и плотностью 1,082 г/мл, если массовая доля гидроксида калия составляет 10 %.

Пример 3. Смешивание растворов с разными концентрациями одного вещества Смешали 300 г раствора с массовой долей хлорида натрия 20 % и 500 г раствора того же вещества с массовой долей 40 %. Вычислите массовую долю хлорида натрия в полученном растворе.

Пример 4. Разбавление водой

ω2 = 0, т.к. в воде не содержится вещество, находящееся в первом растворе.

Какую массу воды надо добавить к раствору гидроксида натрия массой 150 г с массовой долей 10 %, чтобы получить раствор с массовой долей 2 %?

Пример 5. Концентрирование (добавление твердого вещества)

ω2 = 100 %, или 1, т.к. добавляемое вещество чистое.

Какую массу хлорида бария надо добавить к раствору хлорида бария массой 150 г с массовой долей 10 %, чтобы получить раствор с массовой долей 25 %?

Пример 6. Упаривание раствора (частичное выпаривание воды)

Вычислите массовую долю хлорида натрия в растворе, если из 200 г 30 %-го раствора испарилось 50 г воды.

ПРИМЕРЫ ЗАДАЧ

1. Какая масса карбоната натрия (в граммах) потребуется для приготовления 0,5 л 13%-го раствора плотностью 1,13 г/мл?

а) 73,45; б) 50; в) 72; г) 75.

2. Из раствора хлорида бария массой 100 г с массовой долей соли 3 % выпарили 25 г воды и до- бавили в него 15 г соли. Массовая доля соли (в %) в полученном растворе равна:

а) 12; б) 15; в) 18; г) 20.

3. Смешали 120 г раствора серной кислоты с массовой до лей 20 % и 40 г 50%-го раствора того же вещества. Определите массовую долю кислоты (в %) в полученном растворе.

а) 25; б) 27,5; в) 27; г) 29,5.

4. Какая масса азотной кислоты (в граммах) содержится в 1 л ее 20%-го раствора с плотностью 1,05 г/мл?

а) 105; б) 63; в) 210; г) 176.

5. Какая масса соли (в граммах) вводится в организм человека при вливании 353 г 0,85%-го физиологического раствора?

а) 3; б) 6; в) 4; г) 2 г.

6. К 180 г 8%-го раствора хлорида натрия добавили 20 г NaCl. Найдите массовую долю (в %) хлорида натрия в образовавшемся растворе.

а) 17,2; б) 17,4; в) 18; г) 12,7.

7. К раствору хлорида кальция массой 140 г с массовой долей соли 5 % добавили 10 г этой же соли. Определите массовую долю (в %) хлорида кальция в полученном растворе.

а) 13,1; б) 14; в) 11,3; г) 25.

8. Какую массу соли (в граммах) надо добавить к 60 г раствора с массовой долей этой соли 10 %, чтобы получить раствор с массовой долей 40 %?

а) 15; б) 22; в) 17; г) 30.

9. Смешали 200 г 15%-го раствора нитрата хрома(III) и 300 г 20%-го раствора той же соли. Вычислите массовую долю (в %) ни- трата хрома(III) в полученном растворе.

а) 24; б) 18; в) 17,9; г) 18,1.

10. Из 150 г раствора хлорида натрия с массовой долей 5 % выпарили 10 г воды и добавили 5 г той же соли. Вычислите массовую долю (в %) соли в полученном растворе.

а) 8,4; б) 8,6; в) 9; г) 11,2.

11. Смешали 200 г 5%-го и 400 г 12,5%-го растворов серной кислоты. Найдите массу кислоты в полученном растворе (в граммах).

а) 60; б) 98; в) 49; г) 58.

12. При растворении 16 г гидроксида натрия получили 10%- й раствор. Определите массу (в граммах) взятой для этого воды.

а) 126; б) 144; в) 151; г) 164.

13. К 200 г 10%-го раствора ни- трата калия добавили некоторую порцию нитрата калия и получи- ли 20%-й раствор. Найдите массу (в граммах) добавленной порции твердого вещества. а) 2,5; б) 5; в) 25; г) 15.

14. Найдите массу воды (в граммах), которую нужно добавить к 300 г 8%-го раствора сульфата натрия для получения 5%-го раствора.

а) 90; б) 45; в) 18; г) 180.

15. Какая масса раствора (в граммах) получится при упаривании 200 г 5%-го раствора гидроксида калия до 20%-го раствора?

а) 10; б) 45; в) 100; г) 50.

16. 92 мл 10%-го раствора серной кислоты (плотность 1,066 г/мл) полностью нейтрализовали 40%-м раствором гидроксида натрия. Найдите массу затраченного на нейтрализацию раствора гидроксида натрия (в граммах).

а) 10; б) 55; в) 20; г) 30.

17. Определите, какую массу гидроксида калия (в граммах) нужно добавить к 150 г 20%-го раствора гидроксида калия для получения 40%-го раствора.

а) 5; б) 50; в) 56; г) 78.

18. К 200 г 8%-го раствора хлорида натрия добавили 50 г воды. Вычислите массовую долю (в %) соли в образовавшемся растворе.

а) 6,4; б) 6,5; в) 6,1; г) 6,2.

19. Определите массу воды (в граммах), которую надо добавить к 20 г 70%-го раствора уксусной кислоты для получения 5%-го раствора уксуса.

а) 260; б) 130; в) 26; г) 258.

20. Определите массу сахара (в граммах), необходимую для приготовления 0,5 кг 45%-го раствора.

а) 245; б) 225; в) 345; г) 500.

21. Вычислите массовую долю соляной кислоты (в %) в растворе, полученном при растворении 11,2 л (н.у.) хлороводорода в 1 л воды.

а) 1,3; б) 1,6; в) 1,8; г) 3,6.

22. Вычислите массу 40%-го раствора уксусной кислоты (в граммах), которую необходимо добавить к 500 г воды для получения 15%-го раствора.

а) 29; б) 32; в) 48; г) 300.

23. Массовая доля соли в морской воде составляет 3,5 %. Найдите массу соли (в граммах), которая останется после выпаривания 5 кг морской воды.

а) 175; б) 170; в) 167; г) 163.

24. Смешали 250 г раствора гидроксида натрия с массовой долей 16 % и 300 мл раствора (ρ = 1,2 г/мл) с массовой долей того же вещества 20 %. Рассчитайте массу гидроксида натрия (в граммах) в полученном растворе:

а) 120; б) 112; в) 11; г) 115.

25. Какова масса поваренной соли (в граммах), которую следует растворить в 250 г раствора этой соли с массовой долей 10 % для получения раствора с массовой долей 18 %?

а) 22; б) 42,4; в) 24,4; г) 44.

26. К 50 г раствора хлорида кальция с массовой долей 3,5 % добавили 5 г этой же соли и 20 г воды. Определите массовую долю (в %) соли в полученном растворе.

а) 6; б) 7; в) 8; г) 9.

27. Какая масса серной кисло ты (в граммах) содержится в 0,6 л ее 40%-го раствора с плотностью 1,3 г/мл?

а) 63; б) 26; в) 60; г) 312.

28. Найдите массу хлорида натрия (в граммах), который необходимо растворить в 50 г воды для приготовления раствора с массовой долей соли 20 %.

а) 20; б) 12,5; в) 5; г) 24.

29. К 350 г водного раствора этанола с массовой долей 20 % добавили 120 мл спирта (плотность 0,8 г/мл). Рассчитайте массу спирта (в граммах) в полученном растворе.

а) 167; б) 156; в) 166; г) 170.

30. Из 50 г раствора хлорида натрия с массовой долей 2 % выпарили 10 г воды и добавили 5 г этой же соли. Определите массовую долю соли (в %) в полученном растворе.

а) 6,3; б) 13,3; в) 8,9; г) 9,4

Ответы. 1–а, 2–г, 3–б, 4–в, 5–а, 6–а, 7–в, 8–г, 9–б, 10–б, 11–а, 12–б, 13–в, 14–г, 15–г, 16–в, 17–б, 18–а, 19–а, 20–б, 21–в, 22–г, 23–а, 24–б, 25–в, 26–г, 27–г, 28–б, 29–в, 30–б.
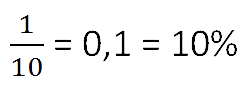
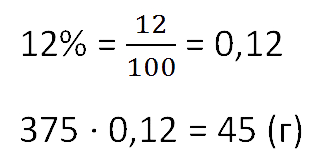
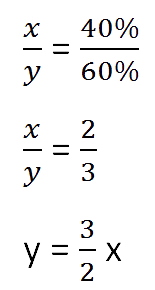
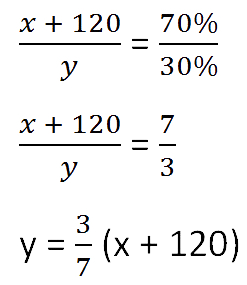
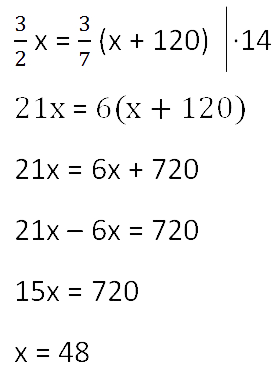
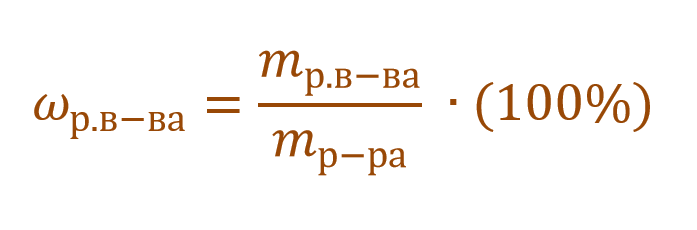
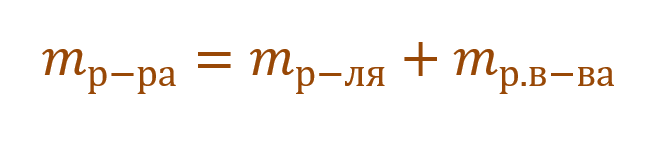
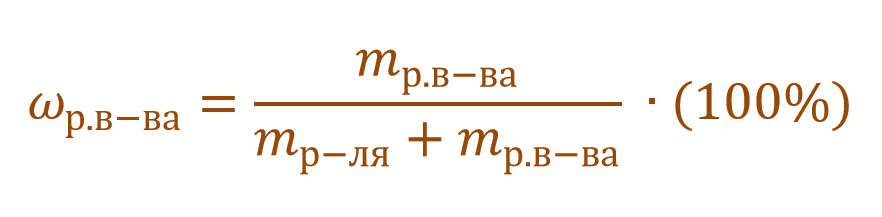
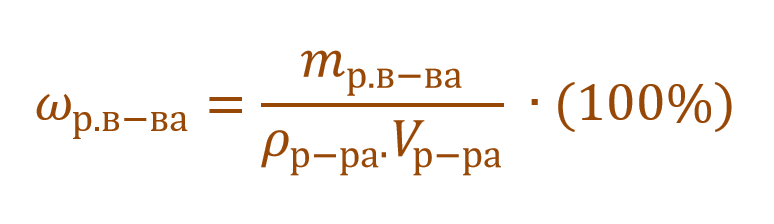
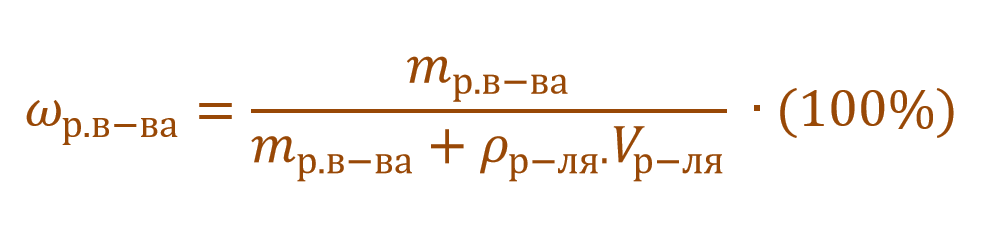
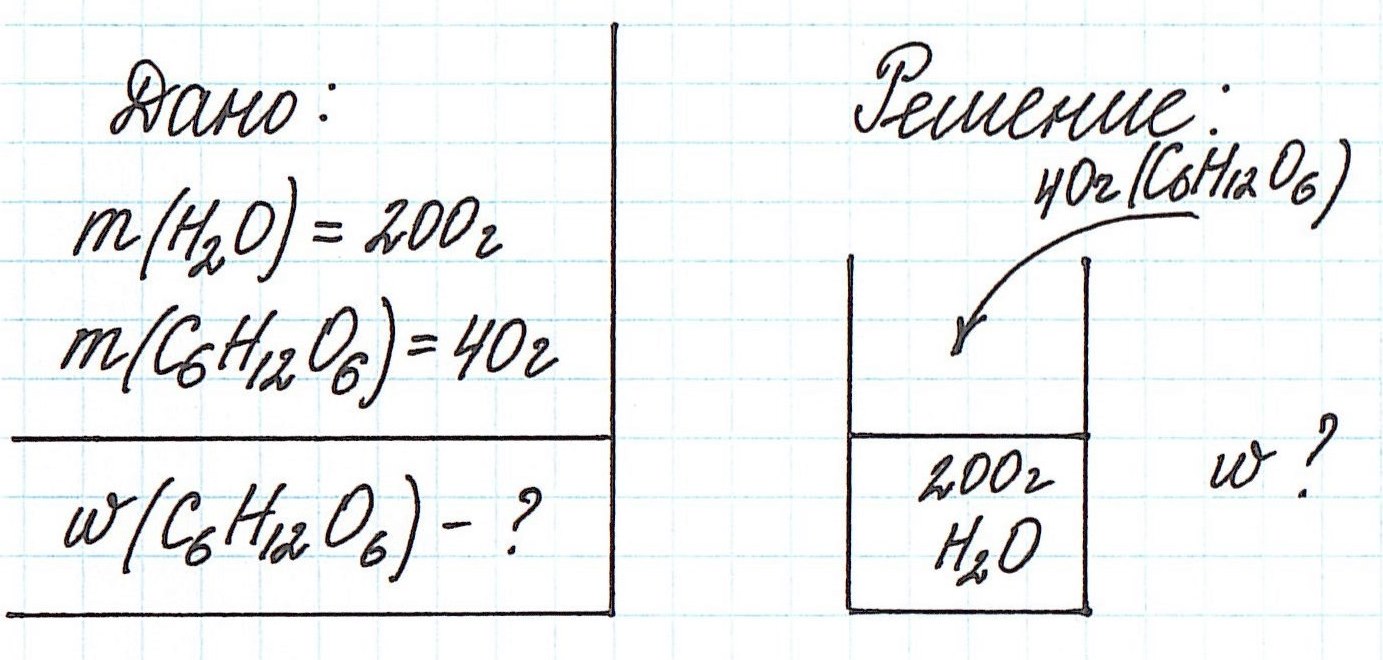
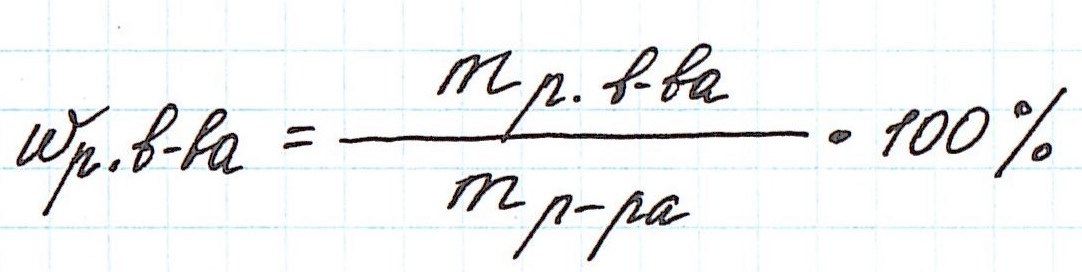
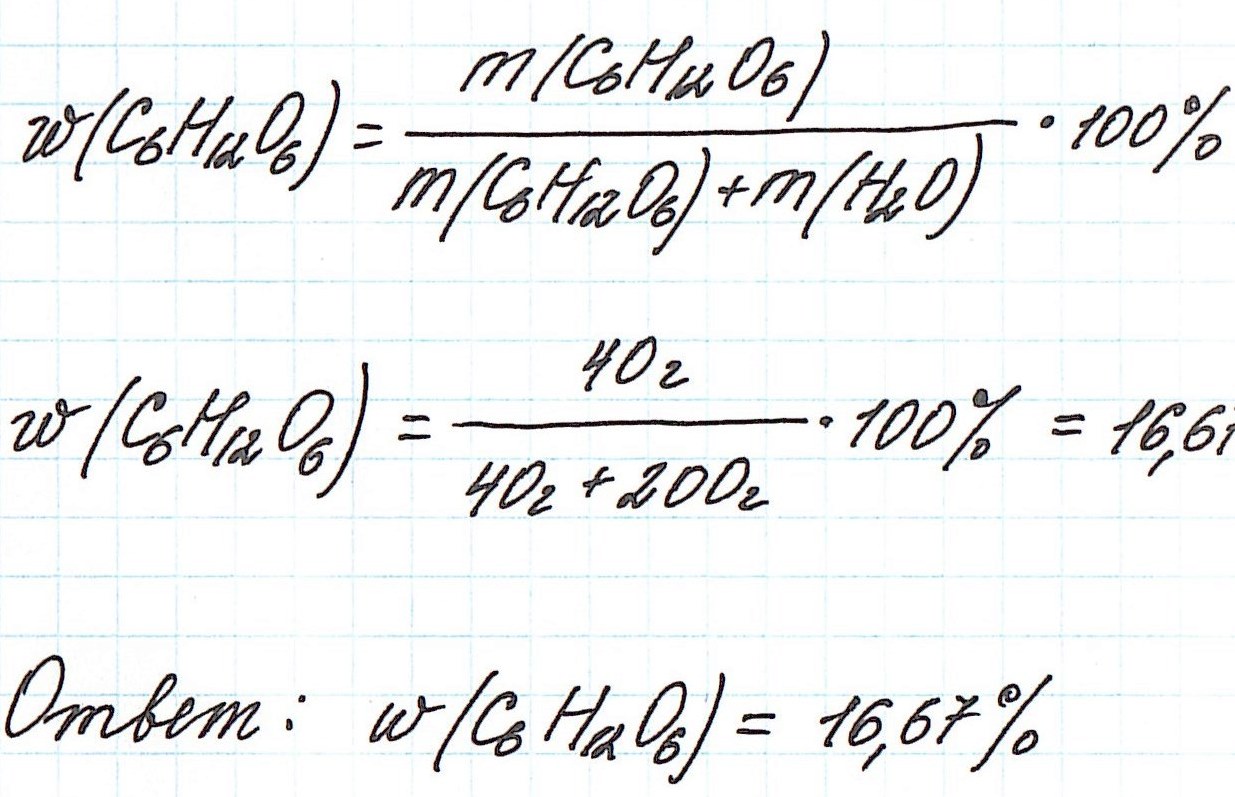
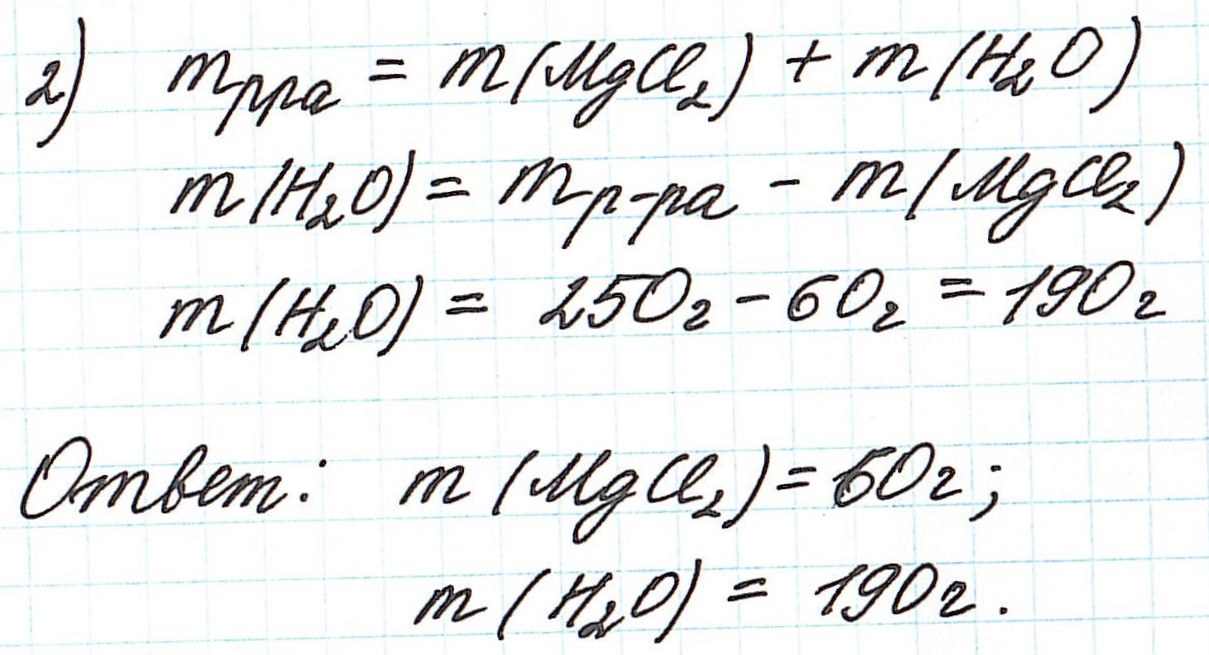
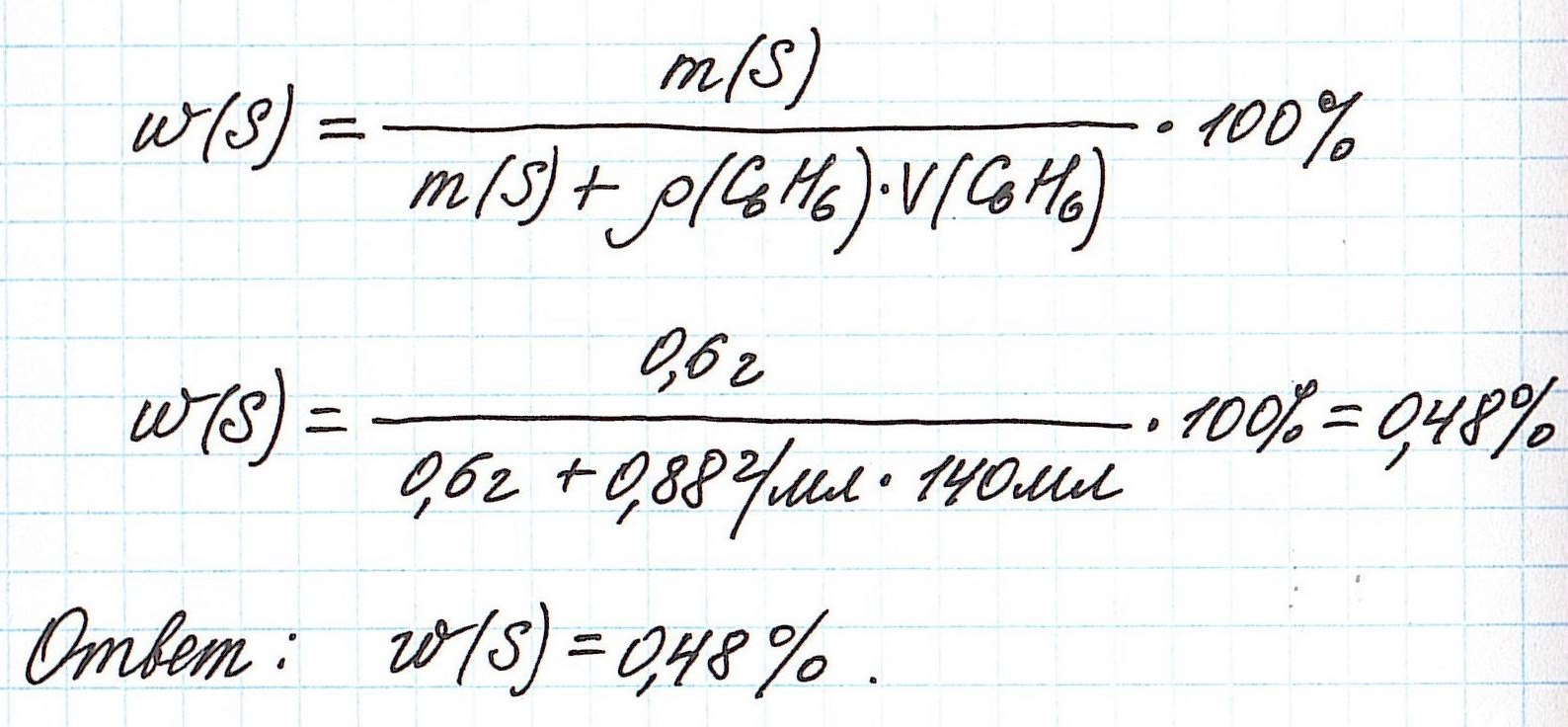
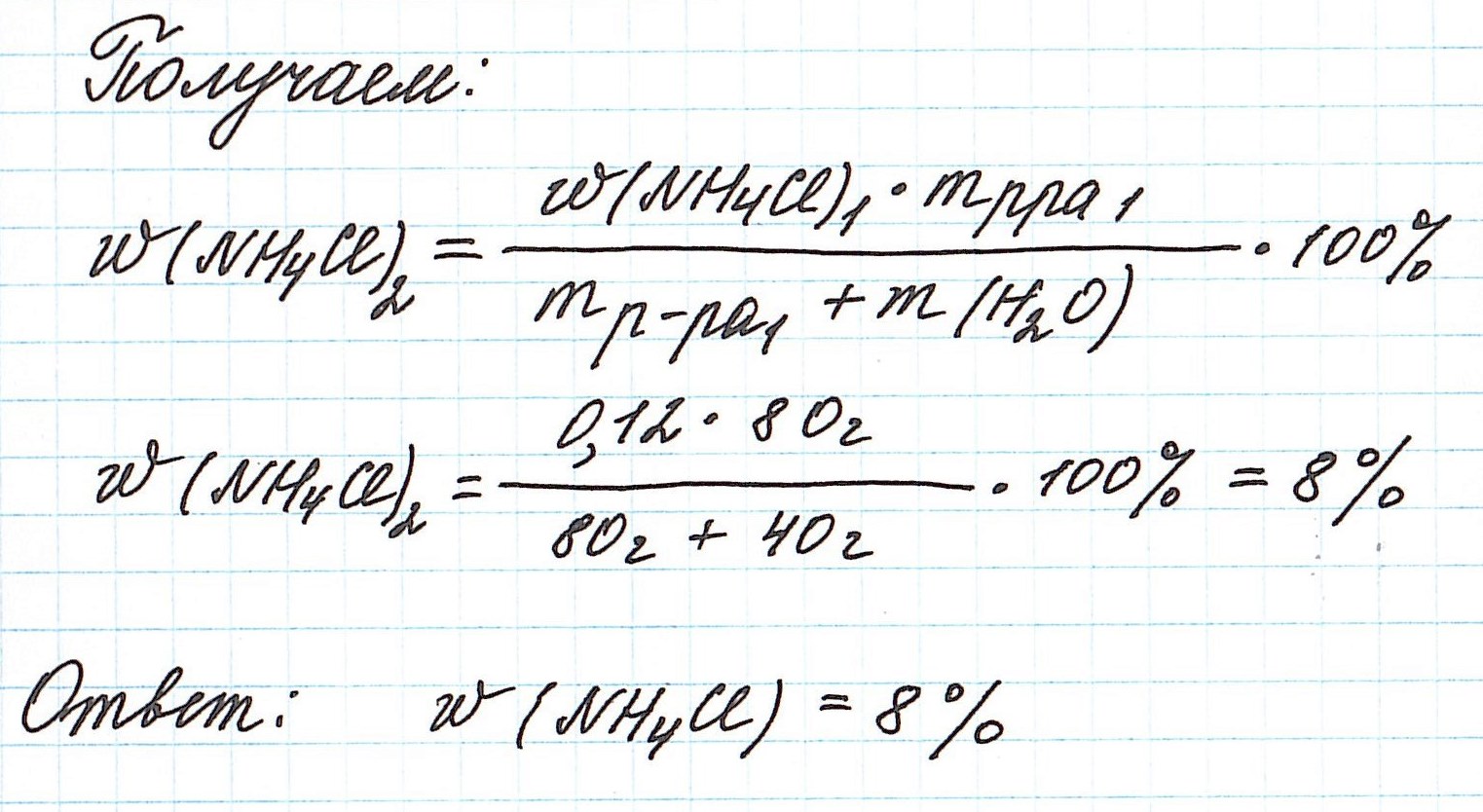
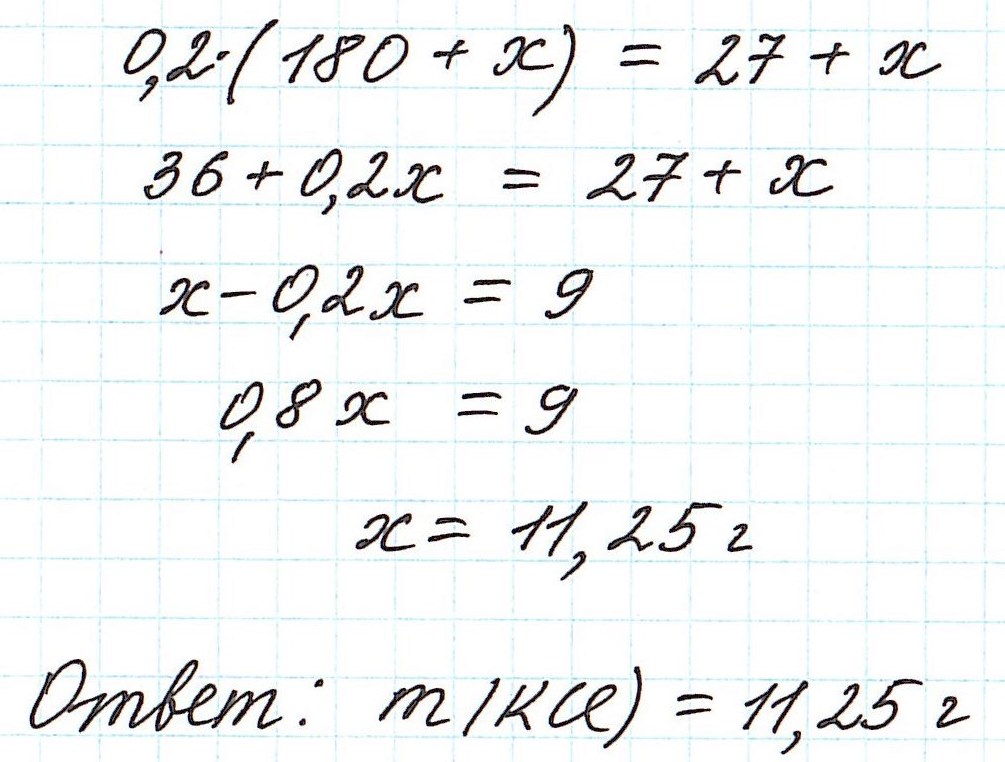
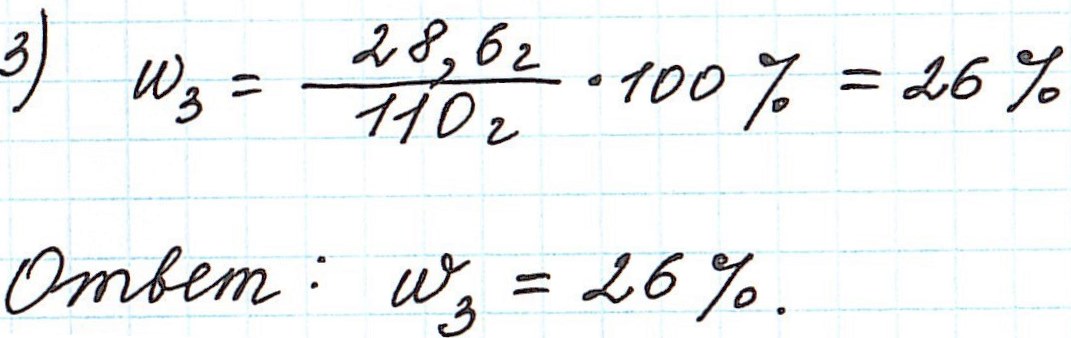
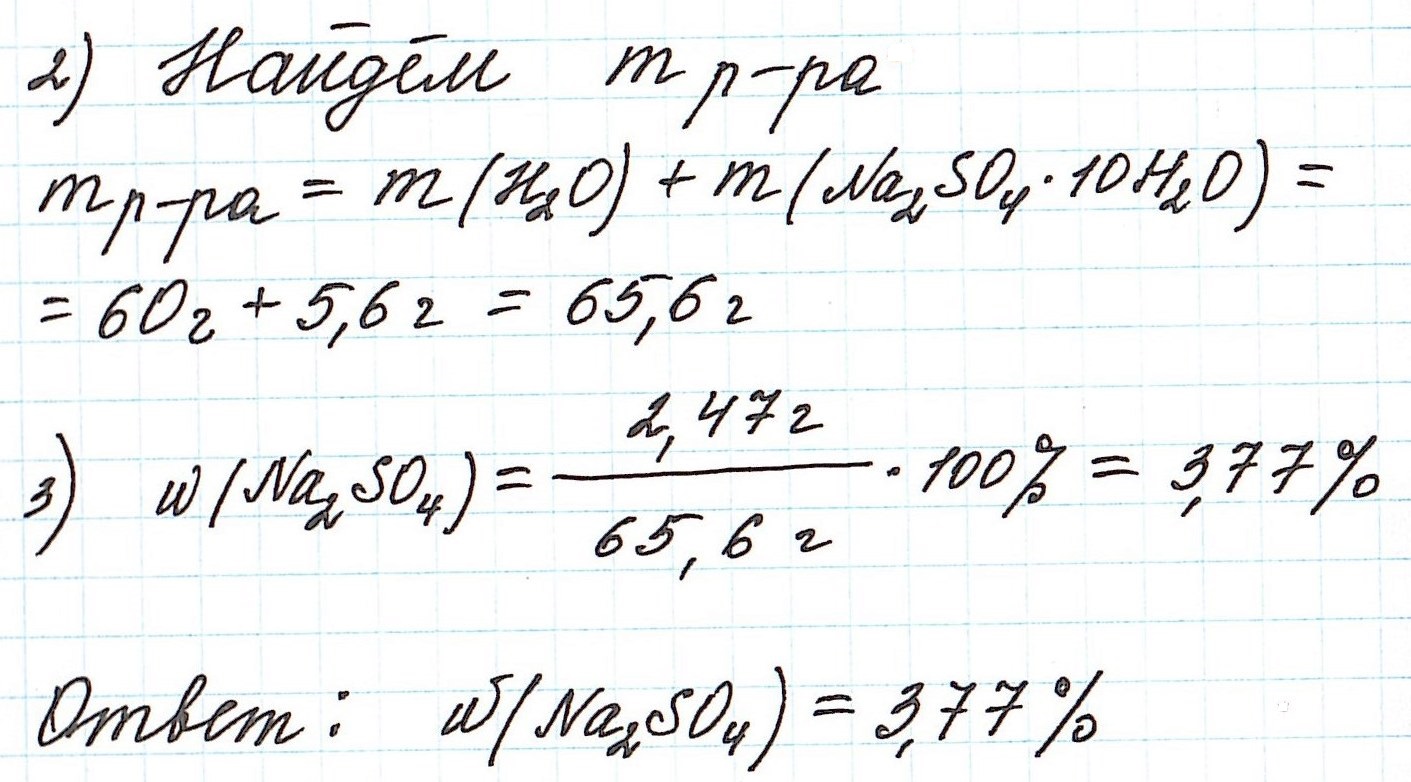
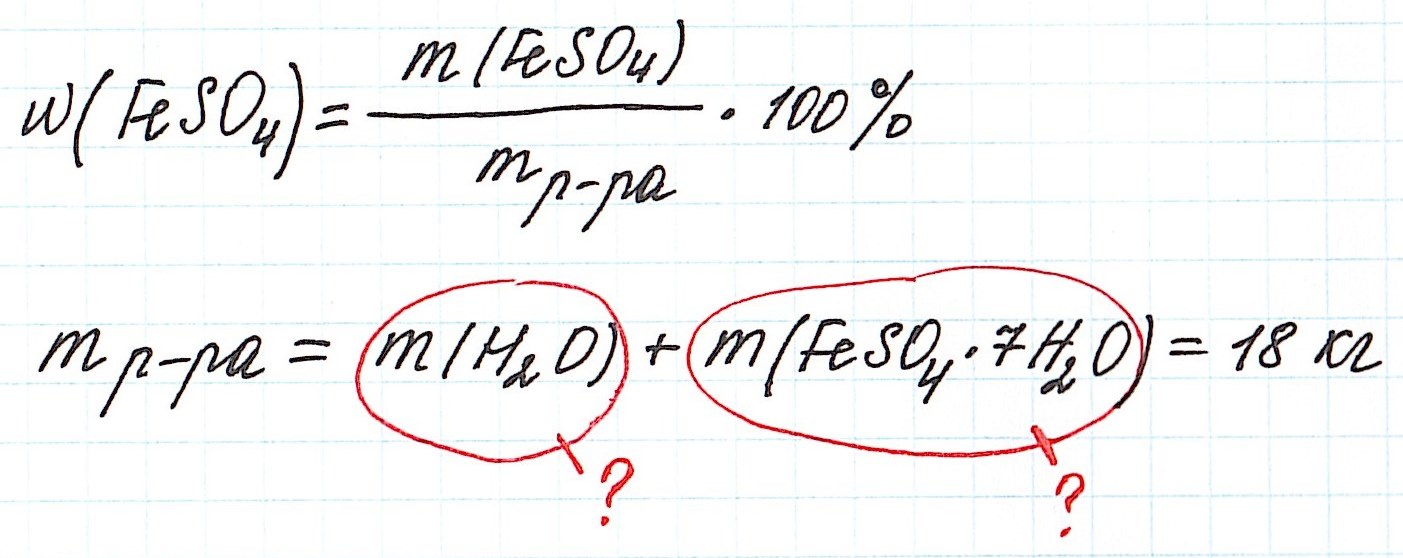
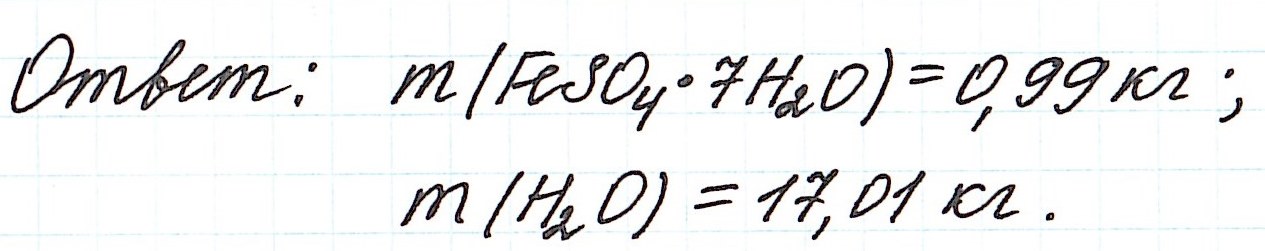