|
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых. Новый ответ. Исправлена механическая ошибка. Дано: длина теплицы: 4,5 метров. Ширина теплицы равна диаметру полуокружья дуги. Дуга = 5,2 м. Вычисляем ширину. Ширина = диаметру = (5,2*2)/π = 10,4/π = 3,31042281631 ~ 3.31 м. Площадь поверхности = длина дуги умножить на длину теплицы = 5,2*4.5 = 23,4 м^2 Площадь входа = половине площади окружности, образованного дугой, но их два — задняя стенка. Принимаю за круг. Радиус равен половине диаметра. r = 3.31/2 = 1.655 м. Нахожу площадь круга. S = π*1.655^2 = 8.60 м^2 ~ 8.6 м^2. Складываю поверхность и торцы: 23,4 + 8,6 = 32 м^2 Плюс запас 10% 10*32/100 = 3,2 м^2 Итог: 32 + 3,2 = 35,2 м^2 ~ 35 м^2 Мой ответ: 35 м^2 квадратных метров плёнки нужно купить для теплицы. Ответ я округлила до целых. автор вопроса выбрал этот ответ лучшим Tanyetta 12 месяцев назад Для того, чтобы посчитать сколько нужно квадратных метров пленки для теплицы, воспользуемся простой математикой. Для начала нам необходимо вспомнить формулу площади круга, S = ПR^2. Нам известно, что длина теплицы составляет 4,5 метров, а длина дуги равна 5,2 метра.
Значит, ответом к задачке будет, 35 метров в квадрате, нам необходимо пленки для теплицы. Пашенька более года назад От нас требуется рассчитать количество пленки для теплицы — в квадратных метрах. Первым делом можно рассчитать площадь, которую составляет крыша.
Также нам нужно подсчитать, сколько пленки пойдет на переднюю и заднюю стенки. Так как по рисунку мы видим, что они образуют полукруг, значит, вместе они составляют целый круг. Значит, площадь круга мы рассчитываем по формуле
Далее добавляем по 10% в запас и получаем: Теперь суммируем:
Ответ:35 Simple Ein более года назад Длина теплицы — 4,5 м. Длина дуги — 5,2 м. Крыша теплицы — прямоугольник. Площадь прямоугольника равна 4,5 * 5,2 = 23,4 м^2. Нам необходимо посчитать площадь половины круга. Площадь круга равна S = ПR^2= 3,14*(5,2/3,14)^2 = 8,61. Пленку необходимо купить с запасом 10 процентов. Получается, что необходимо купить 23,4*1,1 = 25,74. 8,61 * 1,1 = 9,47. Итого 25,74 + 9,47 = 35,21. Округляем до 35. Знаете ответ? |
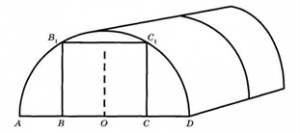
Виктор Николаевич решил построить на дачном участке теплицу длиной 6 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы он заказал металлические дуги в форме полуокружности длиной 5 метров каждая, а также покрытие для обтяжки.
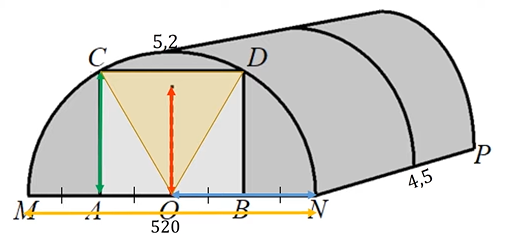
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется сделать вход, который показан на рисунке прямоугольником ВВ1С1С, где точки В,О и С делят отрезок АД на равные части.
Внутри теплицы Виктор Николаевич планирует сделать три грядки по длине теплицы – одну центральную широкую и две по узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых нужно купить тротуарную плитку размером 25 см 25 см.
📜Теория для решения:
Посмотреть решение
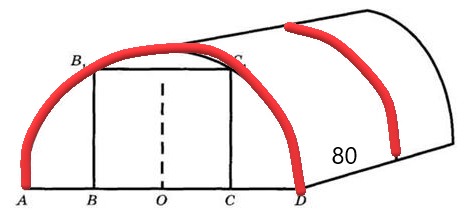
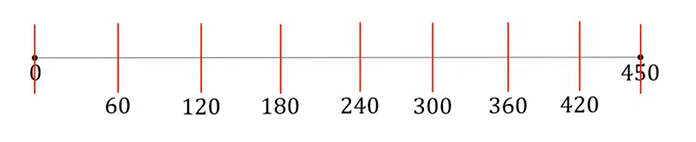
Задание №1. Какое наименьшее количество дуг надо заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение
На рисунке дуги выделены красным цветом и показано, что расстояние между ними не более 80 см.
Зная, что длина теплицы 6 метров, переведем её в сантиметры: 6м=600 см. Теперь разделим 600 см на 80 см, получим 7,5. Округлим до целого числа и получим 8, но это не количество дуг, а количество расстояний (отрезков) между ними. Далее нужно прибавить единицу, чтобы получить точное количество: 8+1=9 дуг.
Если способ с рисунком теплицы не совсем понятен, то можно изобразить дуги точками на отрезке вот таким образом.
Ответ: 9
Задание №2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение
По условию задачи знаем, что в теплице будет три грядки, следовательно, будет две дорожки, ширина которых по условию 50 см. Длина каждой дорожки равна длине теплицы, т.е. 600 см.
Зная длину и ширину дорожки, можно найти её площадь: 600×50=30000 см2. Таких дорожек у нас две, значит 30000×2=60000 см2.
По условию задачи известно, что тротуарная плитка имеет размеры 25 см ×25 см. Можно найти площадь одной плитки: 25 см ×25 см=625 см2.
Теперь находим количество плиток для двух дорожек: 60000:625=96 плиток.
Так как сказано, что плитки продаются в упаковках по 10 штук, то разделим 96 на 10, получим 9,6. Необходимо округлить результат до целого числа, так как отдельно несколько плиток нам не продадут, поэтому 9,6≈10.
Ответ: 10
Задание №3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение
Ширина теплицы – это диаметр полуокружности. По условию задачи Виктор Николаевич покупал дуги длиной 5 метров, значит, длина полуокружности и есть 5 метров.
Вспомним формулу, которая связывает длину окружности и радиус: С=2πR, также можно воспользоваться и формулой С=πd, так как нам надо найти ширину теплицы, т.е. диаметр.
Подставим значения в формулу, помня о том, что полная длина окружности будет равна 10 м: 10=3,14d. Отсюда d=10:3,14=3,184…≈3,2 (так как по условию требуется округлить до десятых).
Ответ: 3,2
Задание №4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение
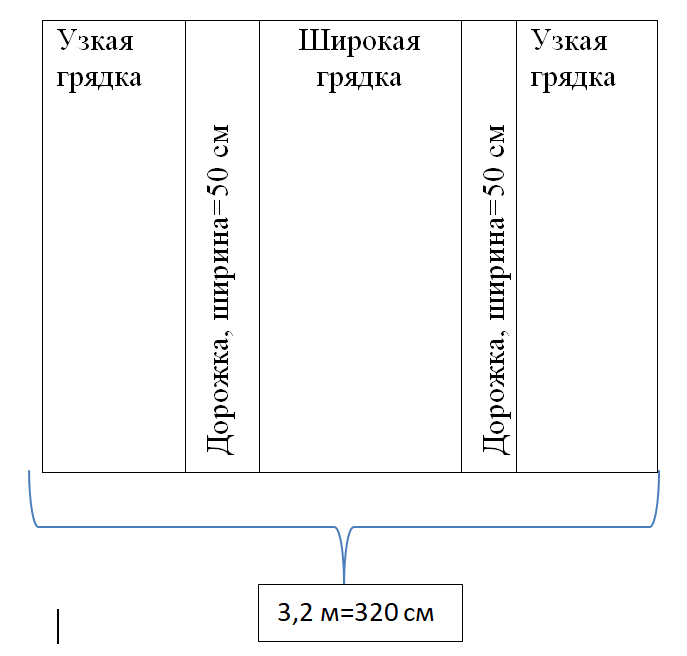
Покажем на рисунке, как выглядят грядки и дорожки внутри теплицы, расставим известные данные: 50 см – по условию, а 320 см – из решения задания №3.
Для удобства решения определим ширину всех грядок вместе, то есть уберем ширину дорожек: 320-50-50=220 см.
По условию задачи ширина центральной грядки относится к ширине узкой грядки как 5:3, т.е. можно сказать, что на центральную грядку (широкую) приходится 5 частей, а на крайние грядки (узкие) по 3 части. Значит, всего на три грядки приходится 3+5+3=11 равных частей. Так как вся ширина грядок 220 см, то 220:11=20 см ширина одной части. Значит, ширина узкой грядки будет равна 20 см×3=60 см.
Ответ: 60 см
Задание №5. Сколько квадратных метров пленки необходимо купить для передней и задней стенок теплицы, если с учетом крепежа ее нужно брать с запасом 15%? Ответ округлить до десятых.
Решение
Передняя и задняя стенки теплицы являются полукругами одинакового диаметра, следовательно, два полукруга вместе – это круг, диаметр которого (ширина теплицы) мы нашли в задаче №3, т.е.3,2 метра. Площадь круга находится по формуле S=πR2. Зная, что диаметр равен 3,2 м, найдем радиус: 3,2:2=1,6 м. Подставим в формулу данные и найдем площадь круга: S=3,14×1,62=8,0384 м2
По условию задачи сказано, что с учетом крепежа пленку надо покупать с запасом 15%. Найдем 15% от данного числа, переведя 15% в десятичную дробь: 0,15×8,0384=1,20576.
Теперь складываем площадь круга и найденные 15%: 8,0384+1,20576=9,24416.
Так как ответ надо округлить до десятых, то получим: 9,24416≈9,2
Ответ: 9,2
Ответ: см. решение
Даниил Романович | Просмотров: 4.9k
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
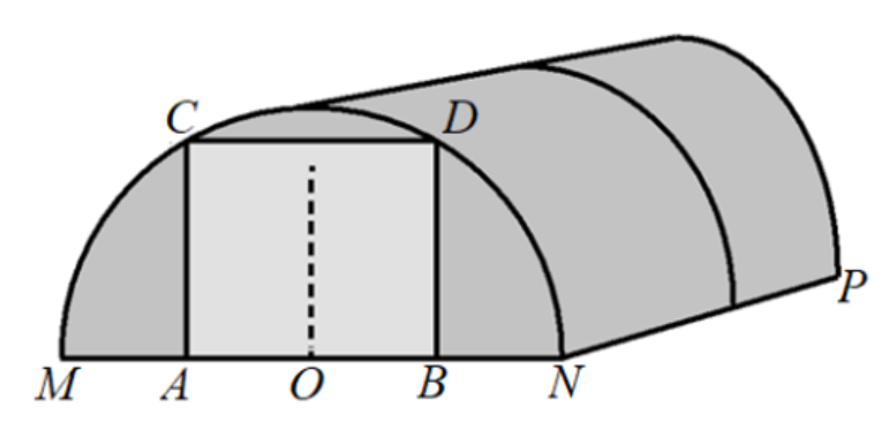
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 5,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB .
Точки A и B — середины отрезков MO и ON соответственно.
Спрятать решение
Решение.
Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 5,8 м и 5,5 м. Вычислим его площадь: S = 5,8 · 5,5 ≈ 32 м2. Площадь стенок — это две полуокружности. Найдем площадь одной окружности: Поскольку плёнки надо купить с запасом, прибавляем по 10% к уже имеющимся цифрам. Получаем:
Ответ: 47.
Примечание Решу ОГЭ.
Мы не знаем, как можно купить круглую плёнку для передней и задней частей теплицы (мы бы купили прямоугольную пленку и разрезали её), но за правдивость условий полностью отвечает составитель задачи. Возможно, это задание о других временах или странах.
В 2022 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада. Обычно статградовские задания, используемые на пробных тестированиях в школах, максимально приближены к реальным экзаменационным вариантам. Рассказываем, как работать с новыми заданиями про теплицу.
Хотите БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ОГЭ по математике 2023 года — приходите на пробное занятие в Lancman School. Решите продолжить готовиться к ОГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия.
Любой вопрос смело пишите сюда. Мы 13 лет готовим к ОГЭ на высокие баллы. Прокачиваем знания даже самых слабых учеников. Гаранитруем получение оценки «5» на ОГЭ. Офисы Курсов ОГЭ Lancman School есть на каждой ветке московского метро.
Если хотите сэкономить, но получить при этом качественную подготовку, записывайтесь на наши онлайн-курсы ОГЭ-2023 по русскому языку, математике, обществознанию и английскому языку.
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение:
Решать подобные задания лучше наглядным способом, то есть нарисовать предварительно дугу и делать на ней необходимые пометки.
Ответ: 9.
2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение:
Длину МN необходимо искать, исходя из дуги, используя формулу длины окружности. Поскольку MN — это полуокружность, то ее длина равна πR.
πR=5,2
3,14R=5,2
R=5,2/3,14
MN=2 × 520/314=520/157
MN=3,31
Ответ: 3,3
3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение:
Площадь участка внутри теплицы представляет собой прямоугольник, и его площадь равна MN × NP.
S=520/157 × 4,5= 2340/157=14,9… При округлению получаем 15.
Можно взять ответ в 3,3 из предыдущего задания для решения.
S=3,3 × 4,5=14,85. При округлении тоже получаем 15.
Ответ: 15.
4. Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Решение:
Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 4,5 и 5,2.
S крыши=5,2 × 4,5=23,4
Остаётся посчитать площадь двух полуокружностей (перед и задняя часть теплицы). Вместе это одна окружность — значит, можно не считать площадь 2 раза.
S стенок=3,14 × (260/157)в квадрате=314/100 × 260/157 × 260/157=1352/157
К данной площади необходимо добавить 10%, поскольку плёнки надо купить с запасом. Прибавляем по 10% к уже имеющимся цифрам.
S крыши=25,74
S стенок=9,47…
Складываем и округляем. Получаем примерно 35 метров плёнки.
Ответ: 35.
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Решение:
Задача геометрическая: нам надо представить, что перед нами равносторонний треугольник.
Итак, перед нами равносторонний треугольник СOD. Найдя его высоту, мы найдём высоту входа в теплицу. Будем использовать формулу высоты равностороннего треугольника. Сторона треугольника COD равна радиусу окружности, которую мы уже знаем (260/157).
h=1,40… Округляем до 1,4.
Ответ: 1,4.
Ваш ребёнок — школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!
Фото: pixabay.com
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
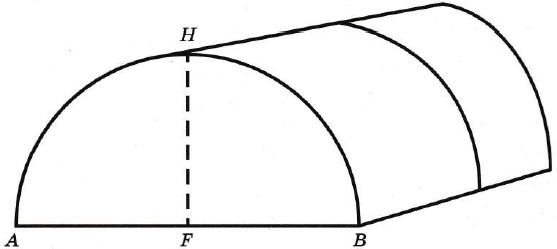
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы – одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.
Источник: ОГЭ Ященко 2022 (36 вар)
Задание 1
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Решение:
Длинна теплицы 4 метра = 400 см. Наименьшее количество дуг по 70 см:
400/70 ≈ 5,7..
Значит минимум 6 дуг, и плюс ещё одна дуга в самом начале теплицы от которой отступали по 70 см. Всего дуг:
6 + 1 = 7
Ответ: 7.
Задание 2
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 12 штук?
Решение:
Длина дорожки равна длине теплицы 400 см, ширина дорожки 40 см. Площадь одной дорожки:
400·40 = 16000 см2
В теплице между грядками будет 2 таких дорожки их общая площадь равна:
16000·2 = 32000 см2
Площадь плитки размером 20 см х 20 см:
20·20 = 400 см2
Всего понадобится плиток:
32000/400 = 80 штук
В одной упаковке 12 штук, необходимо купить:
80/12 ≈ 6,6..
Минимум 7 упаковок.
Ответ: 7.
Задание 3
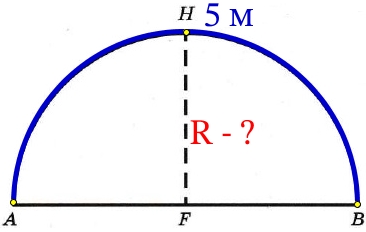
Найдите высоту теплицы. Ответ дайте в метрах с точностью до десятых.
Решение
Знаем, что длина дуги полуокружности равна 5 м, высотой теплицы является радиус R = AD:
Длина всей окружности равна:
5·2 = 10 метров
Формула длины окружности из справочного материала:
l = 2πR
Подставив известные значения в формулу, найдём радиус (он же высота) и округлим до десятых:
10 = 2·3,14·R |:2
5 = 3,14·R
R = 5/3,14 ≈ 1,59… ≈ 1,6
Ответ: 1,6.
Задание 4
Найдите площадь участка, отведённого под теплицу. Ответ дайте в квадратных метрах. Результат округлите до целых.
Решение:
Участок под теплицу является прямоугольником. Его длина по условию равна 4 м, а ширина равна диаметру АВ, зная радиус из задания 3, найдём диаметр:
АВ = 2·R = 2·1,6 = 3,2 м
Найдём площадь участка под теплицу и округлим до целых:
S▭ = 4·3,2 = 12,8 ≈ 13 м2
Ответ: 13.
Задание 5
Сколько квадратных метров плёнки необходимо купить для передней и задней стенок, если с учётом крепежа её нужно брать с запасом 10%? Ответ округлите до десятых.
Решение:
Передняя и задания стенка представляет из себя 2 полукруга (рисунок в задании 3). Вместе они по площади образуют один целый круг, его радиус равен 1,6 м, знаем из задания 3.
Площадь круга по формуле:
S● = πR2
S● = 3,14·1,62 = 3,14·2,56 = 8,0384 м2
Это составляет 100% площади, нам надо взять на 10% больше, т.е. 100 + 10 = 110% (1,10). И округлим до десятых:
S●+10% = 8,0384·1,1 = 8,84224 ≈ 8,8 м2
Ответ: 8,8.
Ответом может быть любое число из отрезка 8,7–8,9.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 86
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.