Как найти скалярный квадрат вектора примеры

Заказать задачи по любым предметам можно здесь от 10 минут

Скалярное произведение векторов

Формула

Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.

Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$

По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.

Примеры решений

В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.

План урока:

Угол между векторами

Понятие скалярного произведения векторов

Скалярное произведение в координатах

Определение перпендикулярности векторов и прямых

Вычисление угла между векторами

Свойства скалярного произведения

Угол между векторами

Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.

Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.

На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:

В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:

Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:

Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что

Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:

Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:

Ответ: а) 45°; б) 90°; в) 135°.

Понятие скалярного произведения векторов

Большое распространение в науке получила математическая операция, именуемая скалярным произведением векторов. В геометрии оно помогает находить угол между векторами, а в физике вычислять некоторые физические величины. В рамках школьной программы его используют для нахождения работы, совершенной той или иной силой. В рамках же более сложных дисциплин, с которыми мало кто сталкивается, оно применяется в квантовой механике и специальных разделах математики – тензорной алгебре, теории многообразий и т. п. Ввел его в науку Уильям Гамильтон в 1846 г, который разрабатывал теорию особых чисел – кватерионов. Они, кстати, используются компьютерами для расчетов трехмерной графики в играх и других приложениях.

Прежде, чем мы научимся применять на практике скалярное произведение, сначала сформулируем правило, позволяющее вычислить его.

Например, пусть есть вектора a и b, причем даны их длины:

Угол между a и b тоже известен и составляет 60°, это записывается таким образом:

Задание. Вычислите скалярное произведение векторов d и f, если их длины составляют 6 и 10 соответственно, а угол между векторами равен 45°.

Решение. Просто подставляем числа из условия в формулу:

Задание. АВС – равносторонний треугольник со стороной 4. Каково скалярное произведение векторов АВ и АС?

Решение. Все углы в равностороннем треугольнике равны 60°, поэтому и угол между АВ и АС также составляет 60°.

Ответ: 8.

Напомним, что косинус, взятый от острого угла – это положительная величина, а косинус тупого угла – это отрицательное число. У прямого же угла косинус равен нулю. Это означает, что по знаку скалярного произведения можно определить тип угла между векторами.

Часто скалярное произведение применяется в физике. Например, с его помощью рассчитывается работа, совершаемая силой при перемещении того или иного тела. И сила, и перемещение – это векторные величины. Чтобы найти работу силы, надо скалярно перемножить вектора силы и перемещения:

Эта формула отражает физический смысл скалярного произведения.

Задание. Под воздействием силы 10Н тело переместилось в горизонтальном направлении на 3 метра. При этом сила образует угол 60° с направлением перемещения тела. Какую работу совершила сила?

Решение.

Скалярное произведение в координатах

Оказывается, что для перемножения векторов достаточно знать только их координаты.

Докажем эту формулу. Сначала рассмотрим случай, когда один из перемножаемых векторов, например a, является нулевым. Тогда у него нулевая длина и нулевые координаты:

Теперь рассмотрим случай, когда оба перемножаемых вектора ненулевые. Тогда отложим их от некоторой точки О и, если вектора неколлинеарны, то мы получим ∆ОАВ:

Для частных случаев, когда a и b коллинеарны (то есть либо сонаправлены, либо противоположно направлены), эта формула также справедлива. Если aи b сонаправлены, то угол α принимается равным нулю (и cosα = 1):

Если же a и b направлены противоположно, то α = 180° (и cosα = – 1):

Итак, мы убедились, что в любой ситуации формула (1) справедлива. При этом вектор АВ можно представить как разность a и b:

Если вектор а имеет координаты {x₁; у₁}, а координаты b– это {x₂; у₂},то координаты их разности a – b будут записываться в виде {х₁ – х₂;у₁ – у₂}. С учетом этого (2) примет вид

В результате нам удалось доказать формулу скалярного произведения через координаты:

Задание. Перемножьте скалярно вектораa и b, если определены их координаты:

Ответ: а) 23; б) 0; в) 5.

Определение перпендикулярности векторов и прямых

Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.

Задание. Проверьте, являются ли перпендикулярными вектора:

Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:

Ответ: а) да; б) нет; в) да; г) нет.

Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?

Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:

Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:

Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).

Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:

Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:

Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.

Ответ: перпендикулярны.

Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями

Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:

Полученный ноль показывает, что исходные прямые перпендикулярны.

Ответ: перпендикулярны.

В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.

Докажем это утверждение. Пусть две прямые заданы уравнениями

Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:

Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:

В результате мы получили доказываемую нами формулу.

Задание. Проверьте, какие из этих пар прямых перпендикулярны:

Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.

Вычисление угла между векторами

Мы научились по координатам векторов определять, перпендикулярны ли они. Однако в более общем случае можно рассчитать угол и между двумя неперпендикулярными векторами.

В самом деле, по известным координатам векторов легко как рассчитать длину каждого из них, так и скалярно перемножить вектора. Тогда из формулы скалярного произведения можно выразить значение косинуса угла между векторами:

Зная же косинус, можно рассчитать и сам угол, используя специальные таблицы либо функцию арккосинуса на калькуляторе.

Задание. Вычислите угол между векторами а{3; 4} и b{8; 15}.

Решение. Сначала рассчитываем длины векторов:

Задание. Точки А(2; 8), В(– 1; 5) и С(3; 1) соединили отрезками и получили ∆АВС. Вычислите угол ∠А в ∆АВС.

Решение.∠А данного треугольника представляет собой угол между двумя векторами АВ и АС. Вычислим координаты этих векторов:

Осталось лишь с помощью калькулятора найти сам ∠А:

Свойства скалярного произведения

Существует несколько важных свойств скалярного произведения. Эти свойства очень схожи с законами алгебры, которые используются при работе с обычными числами.

Переместительный закон легко доказать, опираясь только на определение операции скалярного произведения:

Задание. Известно, что угол между векторами a и с составлет 60°, так же как и угол между векторами b и с. Определены и длины векторов:

Задание. Найдите скалярное произведение векторов p и q, если

Решение. Сначала надо перемножить вектора и раскрыть при этом скобки также, как они раскрываются при перемножении обычных чисел:

Примечание. Иногда скалярное произведение вектора на самого себя именуют скалярным квадратом.

Тогда выражение (1) примет вид:

В сегодняшнем уроке мы узнали, что такое скалярное произведение. Оно имеет много приложений в физике и других науках, в частности, с его помощью вычисляется работа. В геометрии оно помогает вычислять углы между векторами, а значит, и между прямыми. В будущем, при более углубленном изучении геометрии, вы узнаете о существовании других типов произведений векторов – векторном и смешанном.

Для
начала вспомним, какие действия над векторами вам известны.

Итак,
это сложение двух векторов по правилу треугольника или параллелограмма и
нескольких векторов по правилу многоугольника. Вектор разности векторов  мы
получали как вектор суммы векторов .

Также
вам знакомо правило умножение вектора на число.

Сегодня
вы познакомитесь с ещё одним действием над векторами — скалярным умножением
векторов.

Определение.
Скалярным произведением двух векторов называется произведение их длин
на косинус угла между ними.

Скалярное
произведение векторов  обозначают
так .

Или
возможна запись без знака умножения.

Оно
равно произведению длин данных векторов на косинус угла между ними.

Стоит
вспомнить, что угол между векторами получают, откладывая данные векторы от
одной точки. При этом выбирают угол меньший 180°

Обратите
внимание, ранее, при выполнении сложения, вычитания векторов и умножения
вектора на число, результатом каждого из этих действий мы получали некоторый
вектор.

Результатом
же скалярного произведения векторов является число.

Сейчас
подробнее рассмотрим случай, когда скалярное произведение векторов равно 0.

Понятно,
что для этого хотя бы один из множителей должен быть равен нулю.

Такими
будут случаи, когда хотя бы один из векторов в произведении является нулевым.

Если
же векторы  ненулевые,
то косинус угла между ними должен быть равен 0.

Среди
возможных значений градусной меры угла между двумя векторами только лишь косинус
угла в 90° равен 0.

Отсюда
получаем, что векторы  перпендикулярны.

Подытожим.
Скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является
нулевым.

Ну,
а скалярное произведение ненулевых векторов равно нулю тогда и только
тогда, когда эти векторы перпендикулярны.

Из
формулы скалярного произведения также можно заметить, что, если векторы  не
нулевые, то их длины всегда больше нуля, поэтому их произведение тоже
положительно. А вот значение косинуса угла между ними может принимать как
положительные, так и отрицательные значения.

Можно
сказать, что скалярное произведение двух ненулевых векторов больше нуля, если
угол между векторами острый. Равно нулю, если угол между ним прямой. И меньше
нуля, если угол между данными векторами тупой. Ещё раз обратим внимание на то,
что эти заключения верны для ненулевых векторов .

Задача.
Найти скалярное произведение векторов  и
,
пользуясь данными рисунков.

Решение.

а)

б)

в)

г)

Мы
рассмотрели примеры применения формулы скалярного произведения двух векторов и
убедились, что скалярное произведение ненулевых векторов больше нуля, если угол
между ними является острым, равно нулю — если векторы перпендикулярны, и меньше
нуля — если угол между векторами тупой.

А
сейчас рассмотрим сонаправленные векторы  и
.
Запишем формулу их скалярного произведения.

Вы
должны помнить с прошлых уроков, что угол между сонаправленными векторами равен
нулю. А косинус угла в 0° равен 1. Тогда получаем, что скалярное произведение
сонаправленных векторов равно произведению их длин.

Говоря
о противоположно направленных векторах, можно вспомнить, что угол между ними
равен 180°. Значит, косинус равен -1.

Тогда
скалярное произведение противоположно направленных векторов равно .

Что
касается, скалярного произведения вектора на самого себя, то его называют скалярным
квадратом вектора. Этот случай можно рассматривать в контексте
сонаправленных векторов. Действительно, ведь векторы равны, а значит, и
сонаправлены. Такое произведение равно произведению длин данного вектора.

Тогда
получаем, что скалярный квадрат вектора равен квадрату его длины.

Задача.
Найдём скалярные квадраты векторов ,
,
 и
.

Решение.

Скалярное
произведение векторов применяется не только в математике. Например, из курса
механики известно, что работа постоянной силы F
при перемещении из точки М в точку Н равна .

Тем
самым получаем, что работа силы F
равна скалярному произведению вектора силы  и
вектора перемещения .

Вернёмся
к скалярному произведению в математике и решим несколько задач.

Задача.
К одной и той же точке приложены  и
,
действующие под углом в  друг
к другу. ,
.
Найти величину равнодействующей силы .

Решение.

1
способ

,

2
способ

,

Ответ:
.

Задача.
В ,где
,
проведена высота .
Вычислить ,
,
,
.

Решение

,
так как

Подведём
итоги нашего урока.

Сегодня
вы познакомились с новым действием над векторами — скалярным умножением
векторов.

Скалярным
произведением двух векторов называют произведение длин данных векторов на
косинус угла между ними.

Проанализировав
эту формулу, мы заметили, что скалярное произведение равно нулю, если хотя бы
один из векторов сомножителей является нулевым. Ну, а скалярное произведение
ненулевых векторов рано нулю, тогда и только тогда, когда данные векторы
перпендикулярны.

Также,
пользуясь знаниями об углах между сонаправленными и противоположно
направленными векторами, мы выяснили, что скалярное произведение сонаправленных
векторов равно произведению их длин, а скалярное произведение противоположно
направленных векторов противоположно произведению их длин.

Введя
понятия скалярного квадрата вектора, мы получили, что он равен квадрату длины
данного вектора.

Знания
о скалярном произведении векторов можно применять не только на уроках
математики. Так же они широко используются в физике.

Скалярное произведение векторов

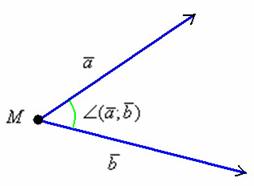
Угол
между векторами 
 может
принимать значения от 0 до 180 градусов
(от 0 до 
 радиан)
включительно. Аналитически данный факт
записывается в виде двойного
неравенства: 
 либо 
 (в
радианах).

В
литературе значок угла 
 часто
пропускают и пишут просто 
.

Определение: Скалярным
произведением двух векторов 
 и 
 называется
ЧИСЛО, равное произведению длин этих
векторов на косинус угла между ними:

Обозначение: скалярное
произведение обозначается через 
 или
просто 
.

Результат
операции является ЧИСЛОМ:
Умножается вектор на вектор, а получается
число. Действительно, если длины
векторов 
 –
это числа, косинус угла – число, то их
произведение 
 тоже
будет числом.

Пример

Найти
скалярное произведение векторов 
 и 
,
если 

Решение: 

Ответ: 

Угол между векторами и значение скалярного произведения

Длины
ненулевых векторов всегда положительны: 
,
поэтому знак может зависеть только от
значения косинуса.

1)
Если угол между
векторами острый: 
  (от
0 до 90 градусов), то 
,
и скалярное
произведение будет положительным: 
.
Особый случай: если векторы сонаправлены,
то угол между ними считается нулевым 
,
и скалярное произведение также будет
положительным. Поскольку 
,
то формула упрощается: 
.

2)
Если угол между
векторами тупой: 
  (от
90 до 180 градусов), то 
,
и, соответственно, скалярное
произведение отрицательно: 
.
Особый случай: если векторы направлены
противоположно, то
угол между ними считается развёрнутым: 
 (180
градусов). Скалярное произведение тоже
отрицательно, так как 

3)
Если угол между
векторами прямой: 
 (90
градусов), то 
 и скалярное
произведение равно нулю: 
.

Скалярное
произведение двух векторов равно нулю
тогда и только тогда, когда данные
векторы ортогональны.
Короткая математическая запись: 

Третий
случай имеет большую практическую
значимость, поскольку
позволяет проверить, ортогональны
векторы или нет.

Скалярный квадрат вектора Что будет, если вектор умножить на самого себя?

Или: 

Число 
 называется скалярным
квадратом вектора 
,
и обозначатся как 
.

Таким
образом, скалярный
квадрат вектора 
 равен
квадрату длины данного вектора:

Из
данного равенства можно получить формулу
для вычисления длины вектора:

Свойства
скалярного произведения.

Для
произвольных векторов 
 и
любого числа 
 справедливы
следующие свойства:

1) 
 –
переместительный или коммутативный закон
скалярного произведения.

2) 
 –
распределительный или дистрибутивный закон
скалярного произведения. Попросту,
можно раскрывать скобки.

3) 
 –
сочетательный или ассоциативный закон
скалярного произведения. Константу
можно вынести из скалярного произведения.

Пример

Найти
скалярное произведение векторов 
 и 
,
если известно, что 
.

Решение: 

(1)
Подставляем выражения векторов 
.

(2)
Раскрываем скобки по правилу умножения
многочленов. Раскрыть скобки нам
позволяет дистрибутивное свойство
скалярного произведения.

(3)
В первом и последнем слагаемом компактно
записываем скалярные квадраты векторов: 
.
Во втором слагаемом используем
перестановочность скалярного
произведения: 
.

(4)
Приводим подобные слагаемые: 
.

(5)
В первом слагаемом используем формулу
скалярного квадрата 
,
о которой не так давно упоминалось. В
последнем слагаемом, соответственно,
работает та же штука: 
.
Второе слагаемое раскладываем по
стандартной формуле 
.

(6)
Подставляем данные условия 
,
и ВНИМАТЕЛЬНО проводим окончательные
вычисления.

Ответ: 

Пример

Найти
длину вектора 
,
если 
.

Решение:

(1)
Поставляем выражение вектора 
.

(2)
Используем формулу длины: 
,
при этом в качестве вектора «вэ» у нас
выступает целое выражение 
.

(3)
Используем школьную формулу квадрата
суммы 
.

(4)
Дальнейшее аналогично действиям из
двух предыдущих задач.

Ответ: 

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Скалярные и векторные величины
2. Скалярное произведение векторов
3. Свойства скалярного произведения векторов
4. Определение скалярного произведения
5. Скалярное произведение векторов, заданных координатами
6. Выражение скалярного произведения в координатах
7. Пусть задана система координат и два вектора для которых

Скалярные и векторные величины

В физике, математике, экономике и других науках встречаются величины двух видов: одни из них характеризуются только числом, а другие — числом и направлением в пространстве.

Величины называются скалярными или скалярами, если каждая из них определяется своим числовым значением в выбранной системе единиц, например, длина, площадь, объем, время, температура.

Величины называются векторными или векторами, если каждая из них определяется числовым значением и направлением. Например, сила, скорость, ускорение.

Определение. Направленный отрезок прямой называется вектором.

Вектор будем обозначать символом . Первая буква означает начало вектора, а вторая — его конец. Вектор также будем обозначать одной малой буквой со стрелкой сверху, например,  (рис. 11).

Рис. 11.

Если начало и конец вектора совпадают, то вектор называется нулевым и обозначается 
или просто 0 . Расстояние между началом и концом вектора называется его длиной, или модулем и обозначается   или  .
Мы будем изучать свободные векторы. Такой вектор можно переносить по его линии действия или параллельно самому себе.

Определение. Векторы, которые находятся на параллельных прямых, или на одной и той же прямой, называются коллинеарными.

Определение. Векторы, которые находятся на параллельных плоскостях или на одной и той же плоскости, называются компланарными.

Соответственно, компланарные векторы, которые приведены к одному и тому же началу, будут находиться на одной плоскости.

Определение. Два вектора равны, если они все одинаково направлены и их модули равны.

Определение. Два вектора, у которых модули равны, а направления противоположные, называются противоположными  и  .
Единичный вектор (орт) вектора   равен    и  обозначается так: 

Скалярное произведение векторов

Некоторые физические величины (сила, смещение, скорость, ускорение и т. д.) характеризуются числом и направлением. Такие величины называются векторами. Векторы используются для представления этих величин.

Напомним, что углом между двумя ненулевыми векторами и называется угол между равными им векторами и отложенными от одной точки (рис. 189).

Если векторы сонаправлены, то угол между ними считается равным нулю; если векторы противоположно направлены, то угол между ними равен 180°; если угол между векторами и равен 90°, то векторы называют перпендикулярными и записывают:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Определение:

Скалярным произведением двух ненулевых векторов называется произведение модулей этих векторов и косинуса угла между ними. Если из двух данных векторов хотя бы один нулевой, то скалярное произведение двух таких векторов считается равным нулю.

Скалярное произведение векторов и обозначают или Таким образом, по определению

Если то скалярное произведение принимает вид называется скалярным квадратом вектора а и обозначается Так как то из получаем то есть скалярный квадрат вектора равен квадрату его модуля. Отсюда Если вектор единичный, то

Возможно вам будут полезны данные страницы:

Свойства скалярного произведения векторов

Для любых векторов пространства выполняются следующие свойства:

1. причем если

2. (коммутативный закон);

3. (ассоциативный закон);

4. (дистрибутивный закон умножения по отношению к сложению векторов).

Справедливость свойств 1-3 скалярного произведения векторов в пространстве доказывается (фактически) точно так же, как и измерения площади.

Свойство 4 доказано в планиметрии для случая, когда векторы и компланарны (лежат в одной плоскости).

Часто используются вытекающие из этих свойств равенства:

Теперь докажем свойство 4 для трех некомпланарных векторов и

Построим параллелепипед такой, что (рис. 190).

Пусть и — середины ребер соответственно Тогда в параллелограмме сумма квадратов длин диагоналей равна сумме квадратов длин всех его сторон, то есть В векторной форме это равенство перепишем так:

Разложив векторы по векторам и запишем:

Используя равенства (2) и затем раскрывая скобки, получим:

откуда: Что и требовалось доказать.

Определение скалярного произведения

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение векторов и обозначают либо Таким образом,

Очевидно, что тогда и только тогда, когда

т. к. нулевой вектор ортогонален любому вектору это утверждение

справедливо и в том случае, когда хотя бы один из векторов и нулевой.

Поскольку то называют скалярным квадратом вектора и обозначают Следовательно,

Зная длины ненулевых векторов и их скалярное произведение, косинус угла между этими векторами можно найти по формуле

Векторные скалярные произведения обладают следующими свойствами:

1. Скалярное произведение векторов коммутативно, т. е.

для любых векторов и

2. Числовой множитель можно выносить за знак скалярного произведения, т. е.

для любых векторов и и любого числа

3. Скалярное произведение дистрибутивно относительно сложения векторов, т. е.

для любых векторов и

4. Скалярный квадрат вектора неотрицателен, т. е.

для любого вектора при этом тогда и только тогда, когда

Скалярное произведение векторов, заданных координатами

Пусть векторы и заданы своими координатами в некоторой прямоугольной декартовой системе координат

Взяв в формуле (1.20) в качестве вектора координатные векторы получим Возведем эти два равенства в квадрат и сложим по частям полученные соотношения, тогда с учетом будем иметь:

Если векторы заданы своими координатами в некоторой пространственной прямоугольной декартовой системе координат то соответствующие формулы имеют аналогичный вид:

Поочередно взяв в формуле в качестве вектора

координатные векторы найдем:

Если возвести в квадрат эти три равенства, а затем сложить по частям, то с учетом (1.24) получим:

Поскольку (рис. 4.3), то скалярное произведение можно представить в двух других видах:

Свойства скалярного произведения:

Если тоНеобходимое и достаточное условие перпендикулярности векторов выражается равенством или Скалярным квадратом вектора называют скалярное произведение вектора на себя:

Скалярный квадрат вектора равен квадрату его длины. Так как

т.е. длина вектора равна корню квадратному из суммы квадратов его координат.

Косинус угла между указанными векторами определяется формулой Механический смысл скалярного произведения: работа производимая силой точка приложения которой прямолинейно перемещается из точки в точку вычисляется по формуле

Примеры с решением

Пример 1.

В четырехугольнике заданы Найти скалярное произведение его диагоналей

Отметим, что (так выражаются диагонали через стороны в векторном виде). Находим

Скалярное произведение двух векторов равно сумме произведений одноименных координат:

Пример 2.

Найти угол между векторами

Из определения скалярного произведения следует, что

В данном случае находим:

Пример 3.

Найти работу силы если точка ее приложения перемещается прямолинейно из точки в точку Находим вектор и вычисляем работу

Пример 4.

Какой угол образуют единичные векторы т и п , если векторы перпендикулярны?

Поскольку то Находим их скалярное произведение

По условию По определению Следовательно,

Выражение скалярного произведения в координатах

Пусть задана система координат и два вектора для которых

По свойствам скалярного произведения

В случае ортонормированного базиса эта формула упрощается, поскольку для попарных скалярных произведений базисных векторов справедливо равенство:

где так называемый символ Кронекера. Откуда, для скалярного произведения векторов в ортонормированном базисе, получаем формулу

из которой следуют полезные соотношения:

Отметим, что последнее равенство в сочетании с условием приводит к неравенству Коши-Буняковского :

Скалярное произведение и векторное произведение является два способом умножения векторов , которые видят большинство применения в физике и астрономии.

Скалярное произведение двух векторов можно построить, взяв компонент одного вектора в направлении других и умножив его раз величиной другого вектора.

Иногда удобно представлять векторы в виде матриц строк или столбцов , а не в единичных векторах, как это было сделано выше при рассмотрении скалярного произведения . Если мы будем рассматривать обычные пространственные векторы как матрицы столбцов их компонентов x, y и z, то транспонирования этих векторов будут матрицами строк.

Задача 1:

Найти расстояние между двумя точками в ортонормированной системе координат, если известны радиус-векторы этих точек.

Решение:

Пусть задана ортонормированная система координат и радиус —векторы двух точек в ней.

Тогда, используя решение задачи 1.7.1., из равенства и свойств скалярного произведения, получаем

Задача 2:

— куб с ребром 2. Точка центр основания Точки и взяты соответственно на отрезках и так, что Найдите: 1) длину отрезка: а) б) в)

2) угол между векторами: а) б) в) (рис. 194).

Решение:

Введем базис

Так как грани куба — равные квадраты со стороной 2, то

Рассмотрим некоторые случаи.

1. б) Длина отрезка равна длине вектора Разложим вектор по базису По правилу ломаной Тогда Учитывая получаем откуда Следовательно,

2. а) Обозначим Тогда

Находим Учи тывая получаем

Получаем

Ответ: 1. б) . 2. а) 60°

Задача 3:

Все ребра правильной четырехугольной пирамиды равны 1 (рис. 195). Точка — центр грани Точки — середины ребер соответственно Найдите: а) длину отрезка б) длину отрезка

в) угол

между векторами г) угол между медианой грани и высотой грани

При решении пунктов а) и в) используйте векторы.

Решение:

Введем базис Так как боковые грани пирамиды — правильные треугольники, а основание — квадрат, то

Поэтому имеем

а) Длина отрезка равна длине вектора Разложим этот вектор по базису

По правилу треугольника — По правилу параллелограмма Значит, Тогда

Учитывая получаем откуда

в) Пусть Тогда Разложим векторы по базису Имеем:

Находим:

Принимая во внимание получаем:

Поэтому значит,

Ответ: a)