1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы,
для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и
):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Системы счисления. Перевод из одной системы в другую.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Основы систем счисления
Время на прочтение
11 мин
Количество просмотров 503K
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палецзарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Методы определения значения числа:
- Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
- Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
- Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.
Помимо цифирных, существуют и буквенные (алфавитные) системы счисления, вот некоторые из них:
1) Славянская
2) Греческая (ионийская)
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Qn (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:
- Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
- Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.
Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 100111102, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2n, где n — номер разряда, 010 011 110 = (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) = 2368. Получается, что 100111102 = 2368. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 2368 = (10 011 110)2-8.
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Имеется число a1a2a3 в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bn, где n — номер разряда. Таким образом, (a1a2a3)b = (a1*b2 + a2*b1 + a3*b0)10.
Пример: 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Целая часть:
- Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
- Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.
Дробная часть:
- Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
- Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
Пример: переведем 1510 в восьмеричную:
158 = 1, остаток 7
18 = 0, остаток 1
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2n, где n — номер разряда.
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Пример: 101,0112 = (1*22 + 0*21 + 1*20), (0*2-1 + 1*2-2 + 1*2-3) = (5), (0 + 0,25 + 0,125) = 5,37510
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20), (0*22 + 1*21 + 0*20) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Содержание
Введение
История происхождения
систем счисления
Основные позиционные
системы счисления
Перевод чисел из одной
системы счисления в другую
Алгоритм перевода
целого числа из десятичной системы счисления — в двоичную, восьмеричную или
шестнадцатеричную.
Алгоритм перевода
правильной дроби из десятичной системы счисления — в двоичную, восьмеричную или
шестнадцатеричную.
Алгоритм перевода
обычной дроби из десятичной системы счисления — в двоичную, восьмеричную или
шестнадцатеричную.
Алгоритм перевода чисел
из любой системы счисления в десятичную систему.
Арифметические действия
с числами в различных системах счисления
Сложение
Вычитание
Умножение
Деление
Практикум
Перевод чисел из одной
системы счисления в другую
Задания на
арифметические действия
Текстовые задания
Задание на координатной
плоскости
Комплексные
самостоятельные работы – 1 комплект
Комплексные
самостоятельные работы – 2 комплект
Решения
Перевод чисел из одной
системы в другую
Задания на
арифметические действия
Задание на координатной
плоскости
Комплексные
самостоятельные работы – 1 комплект
Комплексные
самостоятельные работы – 2 комплект
Список использованных
источников
Введение
В школьном курсе информатики и математики, к
сожалению, теме «Системы счисления» уделяется совсем немного времени. Хотя она
является одной из базовых для изучения способов и методов хранения информации в
компьютере. И на ДПА практически в каждом билете есть задание по этой теме.
Поэтому основная цель данной работы и заключается в том, чтобы помочь учителям
и учащимся разобраться в этой теме более подробно и иметь возможность более
качественно подготовиться к ДПА.
«Все есть число», — говорили пифагорийцы,
подчеркивая необычайно важную роль чисел в практической деятельности. Известно
множество способов представления чисел. В любом случае число изображается
символом или группой символов (словом) некоторого алфавита. Такие символы
обычно называют цифрами. Для представления чисел используются непозиционные и
позиционные системы счисления.
Основное отличие этих систем счисления заключается в
том, что в позиционных системах счисления одна и та же цифра в
записи числа имеет различные значения в
зависимости от того места (разряда), где она расположена.
А в непозиционных системах счисления значение цифры не зависит от ее
местоположения в записи числа.
В данном пособии мы не будем с вами сильно
углубляться в историю происхождения систем счисления, а больше займемся
практической частью данной темы, т. е. тем, что будет необходимо для решения
задач по системам счисления.
История происхождения систем счисления
В древние времена, когда люди начали считать,
появилась потребность в записи чисел. Первоначально количество предметов
отображали равным количеством каких-нибудь значков: насечек, черточек, точек.
Изучение археологами «записок» времен
палеолита на кости, камне, дереве показало, что люди стремились группировать
отметки по 3, 5, 7, 10 штук. Такая группировка облегчала счет. Люди учились
считать не только единицами, но и тройками, пятерками и пр. Поскольку первым
вычислительным инструментом у человека были пальцы, поэтому и счет чаще всего
вели группами по 5 или 10 предметов.
В дальнейшем свое название получили десяток десятков
(сотня), десяток сотен (тысяча) и так далее. Такие узловые числа для удобства
записи стали обозначать особыми знаками — цифрами. Если при счете предметов их
оказывалось 2 сотни, 5 десятков и еще 4 предмета, то при записи этой величины
дважды повторяли знак сотни, пять раз — знак десятков и четыре раза знак единицы.
В таких системах счисления от положения знака в записи числа не зависит
величина, которую он обозначает; поэтому они называются непозиционными
системами счисления. Непозиционными системами пользовались древние египтяне,
греки, римляне и некоторые другие народы древности.
До нас дошла римская система записи чисел (римские
цифры). Первые двенадцать натуральных чисел в римской системе записываются так:
I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII.
Примеры записи чисел XXVIII – 28, MCMXXXV – 1935. С
этими числами очень трудно производить арифметические действия. По этой причине
в настоящее время римская система счисления используется там, где это
действительно удобно: в литературе (нумерация глав), в оформлении документов
(серия паспорта, ценных бумаг и др.), в декоративных целях – на циферблате
часов, в ряде других случаев.
На Руси вплоть до XVIII века использовалась
непозиционная система славянских цифр. Буквы кириллицы (славянского алфавита)
имели цифровое значение, если над ними ставился специальный знак ~ титло.
Например: — 1,
— 4,
— 100. Интересно, что существовали обозначения
очень больших величин. Самая большая величина называлась «колода» и
обозначалась знаком . Это
число равно 105. Считалось, что «боле сего несть человеческому
уму разумевати».
Непозиционные системы счисления были более или менее
пригодны для выполнения сложения и вычитания, но совсем не удобны при умножении
и делении.
Впервые идея позиционной системы счисления возникла в
древнем Вавилоне.
Система счисления, применяемая в современной
математике, является позиционной десятичной системой. Ее основание равно
десяти, так как запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Хотя десятичную систему принято называть арабской, но
зародилась она в Индии, в V веке. В Европе об этой системе узнали в XII веке из
арабских научных трактатов, которые были переведены на латынь. Этим и
объясняется название «арабской цифры». Однако широкое распространение
в науке и в обиходе десятичная позиционная система получила только в XVI веке.
Эта система позволяет легко выполнять любые арифметические вычисления,
записывать числа любой величины. Распространение арабской системы дало мощный
толчок развитию математики.
Очевидно, что число «десять» — не
единственное возможное основание позиционной системы. Известный русский
математик Н.Н.Лузин так выразился по этому поводу: «Преимущества
десятичной системы не математические, а зоологические. Если бы у нас на руках
было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной
системой».
За основание позиционной системы счисления можно
принять любое натуральное число больше 1.
Особый интерес представляет так называемая
“вавилонская”, или шестидесятеричная система счисления, существовавшая в
Древнем Вавилоне. Мнение историков по поводу того, как именно возникла эта
система счисления, расходятся. Существуют две гипотезы. Первая исходит из того,
что произошло слияние двух племен, одно из которых пользовалось шестеричной,
другое – десятичной. Шестидесятеричная система счисления в данном случае могла
возникнуть в результате своеобразного политического компромисса. Суть второй
гипотезы в том, что древние вавилоняне считали продолжительность года равной
360 суткам, что связано с числом 60. Отголоски использования этой системы
счисления дошли до наших дней. Например, 1 час = 60 минутам. В целом
шестидесятеричная система счисления громоздка и неудобна.
Довольно широкое распространение имела
двенадцатеричная система счисления. Происхождение ее тоже анатомическое. Подумайте,
где у человека удобно считать до 12? Считали фаланги пальцев на руке кроме
большого. 4 пальца по три фаланги всего 12. Элементы двенадцатеричной системы
счисления сохранились в Англии в системе мер (1 фут = 12 дюймов) и в денежной
системе (1 шиллинг = 12 пенсам). Где вы еще встречали счет по 12? Нередко и мы
сталкиваемся в быту с двенадцатеричной системой счисления: чайные и столовые
сервизы на 12 персон, комплект носовых платков – 12 штук.
По свидетельству известного исследователя Африки
Стэнли, у ряда африканских племен была распространена пятеричная система
счисления, Долгое время пользовались пятеричной системой счисления и в Китае.
Очевидна связь этой системы со строением человеческой руки.
У ацтеков и майя – народов, населявших в течение
многих столетий обширные области Американского континента и создавших там
высочайшую культуру, в том числе и математическую, была принята двадцатеричная
система счисления. Также двадцатеричная система счисления бала принята и у
кельтов, населявших Западную Европу начиная со второго тысячелетия да нашей
эры. Основу для счета в этой системе счисления составляли пальцы рук и ног.
Некоторые следы двадцатеричной системы счисления кельтов сохранились во
французской денежной системе: основная денежная единица, франк, делится на 20
(1 франк = 20 су).
Основные позиционные системы
счисления
Если в
математике возможно использование и позиционных и непозиционных систем счисления, то в информатике для представления информации в так называемом «компьютерном» виде используются только позиционные системы счисления.
С понятием системы счисления связано еще понятие основания системы счисления. Это число, которое показывает, сколько символов используется при записи числа в данной системе счисления. Причем сначала используются арабские цифры, начиная с нуля, а когда их становиться мало, то добавляют буквы латинского алфавита.
Например,
в двоичной системе счисления используется только два символа: 0 и 1, а в шестнадцатеричной системе счисления к базовым десяти цифрам (0…9) уже добавляются 6 букв латинского алфавита (A,B,C,D,E,F) чтобы в итоге получить 16 символов для записи чисел. Собственно говоря, системы счисления используются не только для записи чисел в компьютерном виде, но и для кодирования информации любого вида в памяти компьютера — у любого вводимого символа в компьютер, будь то число, или буква, или звук и т. д., есть свой числовой код, по которому компьютер и различает что же именно вы ему ввели.
Наиболее употребляемыми в настоящее время позиционными системами являются:
·
1 — единичная (как позиционная может и
не рассматриваться; счёт на пальцах, зарубки, узелки «на память» и др.);
·
2 — двоичная (в
дискретной математике, информатике, программировании);
·
3 — троичная;
·
4 — четверичная;
·
5 — пятеричная;
·
8 — восьмеричная;
·
10 — десятичная (используется повсеместно);
·
12 — двенадцатеричная (счёт дюжинами);
·
16 — шестнадцатеричная (используется в программировании, информатике, а также в
шрифтах);
·
60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
Ниже приведем таблицу, в которой описаны основные позиционные системы счисления, которые используются в информатике:
|
Система счисления |
Основание |
Алфавит |
|
Десятичная |
10 |
0;1;2;3;4;5;6;7;8;9 |
|
Двоичная |
2 |
0; 1 |
|
Восьмеричная |
8 |
0;1;2;3;4;5;6;7 |
|
Шестнадцатеричная |
16 |
0;1;2;3;4;5;6;7;8;9;A;B;C;D;E;F |
Таблица 1. Наиболее часто используемые позиционные
системы счисления
В таблице ниже приводятся десятичные числа от 0 до 15 и их эквивалент в различных системах счисления:
|
Десятичная система счисления |
Двоичная система счисления |
Восьмеричная система счисления |
Шестнадцатеричная система счисления |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
Таблица 2. Эквивалент чисел от 0 до 15 в различных
системах счисления
Перевод
чисел из одной системы счисления в другую
При переводе из одной системы счисления в другую
целого числа в результате так же
получится целое число.
Есть два основных способа перевода чисел из одной
системы счисления в другую. Первый способ заключается в том, что наша родная
десятичная система счисления используется как своеобразный буфер обмена, а во
втором способе число разбивается на определенные группы цифр, а далее каждая из
этих групп переводится в соответствующий ей символ новой системы счисления.
Предлагается к рассмотрению первый способ, поскольку, исходя из опыта
преподавания этой темы ученикам разных возрастных групп, он гораздо проще и
легче воспринимается и запоминается, т. к. для второго способа требуется
знание или наличие таблиц соответствия цифр в различных системах счисления
(см. Табл. 2).
Перевод целого числа из десятичной системы счисления
в любую другую осуществляется с помощью обыкновенного деления в столбик,
которое изучается еще в начальной школе, по следующему алгоритму.
Алгоритм
перевода целого числа из десятичной системы счисления — в двоичную,
восьмеричную или шестнадцатеричную.
1)
исходное целое десятичное число
делится на основание системы счисления, в которую переводится (на 2, 8 или 16);
получается частное и остаток;
2)
далее последовательно все
частные от целочисленного деления так же делятся на основание системы счисления,
в которую переводится (на 2, 8 или 16) до тех пор, пока частное не станет
меньше этого основания (меньше 2, 8-ми или 16-ти);
3)
затем формируется результат:
сначала записывается последнее полученное частное (меньшее нового основания), а
затем переписываются все остатки от деления начиная с последнего (см. рис. 1)
 |
Рис. 1. Перевод целых чисел из десятичной системы
счисления в двоичную.
Аналогично переводятся числа из десятичной системы
счисления в восьмеричную и шестнадцатеричную, только делить надо
соответственно на 8 или на 16. При переводе в шестнадцатеричную систему когда
формируется результат после деления на 16, те остатки от деления, которые
больше 9-ти, записываются соответствующими буквами латинского алфавита (см.
табл. 2 рис. 2, рис. 3)
 |
Рис. 2. Пример перевода числа 75 из десятичной системы
счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления
 |
Рис. 3. Пример перевода числа 315 из десятичной
системы счисления в восьмеричную и шестнадцатеричную системы счисления
Перевод дробного числа из десятичной системы счисления
в любую другую осуществляется с помощью обратной операции, умножения, по
следующему алгоритму. Результатом
такого перевода так же будет правильная дробь.
Алгоритм
перевода правильной дроби из десятичной системы счисления — в двоичную,
восьмеричную или шестнадцатеричную.
1)
дробную часть десятичного
числа и получаемые дробные части произведений надо последовательно умножать на
основание новой системы (2, 8 или 16) до тех пор, пока дробная часть
произведения не станет равной нулю или не будет достигнута требуемая точность
представления числа в новой системе счисления;
2)
полученные целые части
произведений являются цифрами числа в новой системе счисления;
3)
затем снова-таки
формируется результат: из полученных целых частей произведений составляется
дробная часть числа в новой системе счисления, начиная с целой части первого
произведения (см. рис. 4, рис. 5, рис. 6).
 |
Рис. 4. Пример перевода числа 0,1875 из десятичной
системы счисления в двоичную, восьмеричную и шестнадцатеричную системы
счисления
Рис. 5. Пример перевода числа 0,847 из десятичной
системы счисления в двоичную систему счисления. Перевод выполнялся до четырех значащих цифр после запятой
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата.
Рис. 6. Пример перевода числа 0,847 из десятичной
системы счисления в шестнадцатеричную систему счисления. Перевод выполнялся до трех значащих цифр после запятой
Алгоритм
перевода обычной дроби из десятичной системы счисления — в двоичную,
восьмеричную или шестнадцатеричную.
При переводе дробного числа отдельно переводится целая часть числа
по алгоритму перевода целых чисел,
отдельно – дробная
по алгоритму переводя правильных дробей,а затем результаты
вычислений складываются.
Пример.
Перевести десятичное число 315,1875 в восьмеричную и в
шестнадцатеричную системы счисления. Из рассмотренных выше примеров следует:
315,187510 = 473,148 =13B,316 (см. рис. 7)
 |
Рис. 7. Пример перевода числа 351,1875 из десятичной
системы счисления в восьмеричную и шестнадцатеричную системы счисления
Алгоритм
перевода чисел из любой системы счисления в десятичную систему.
Для того, чтобы перевести число из любой системы
счисления в десятичную необходимо воспользоваться формулой представления этого
числа через его цифры с помощью следующего многочлена относительно q:
Aq = a1*q0 + a2*q1 +…+ an*qn
,
а затем произвести
вычисления.
На практике же это все выглядит не таким устрашающим,
а очень даже понятным. Давайте сначала посмотрим на Рис. 8 с примером перевода
числа из двоичной системы счисления в десятичную.
Рис. 8. Пример перевода числа из
двоичной системы счисления в десятичную систему счисления
А теперь попробуем описать алгоритм проведенных
вычислений:
1)
сначала записывается
исходное число и в конце к нему в виде нижнего индекса дописывается основание
той системы счисления, в которой оно записано (в формуле – это величина q);
2)
затем сверху или снизу
числа к каждой его цифре от конца к началу дописывается номер ее позиции
начиная с 0-вой;
3)
если число дробное, то
номера позиции надписываются от запятой в одну и в другую стороны – для целой
части числа надписываются положительные числа, начиная с 0, а для дробной части
надписываются отрицательные числа, начиная с -1.
4)
далее производятся
вычисления следующим образом – отдельно взятая цифра числа умножается на
основание этого числа, возведенное в ту степень, которая была написана выше или
ниже этой цифры (см. п.2) данного алгоритма), затем ставится знак «+» и
повторяются эти же действия со следующей цифрой числа;
5)
действия из п. 3)
повторяются до тех пор, пока не закончатся цифры в числе, а потом необходимо
просто это все вычислить;
6)
в итоге получится число,
записанное в десятичной системе счисления.
Давайте попробуем этот алгоритм разобрать на примерах.
Пример 1. Перевести число 1101102 из двоичной
системы счисления в десятичную.
Решение:
5 4 3 2 1 0
1 1 0 1 1 0 2 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20
=32+16+4+2=5410
Ответ:
1101102 = 5410
Пример 2. Перевести число 101,012 из двоичной
системы счисления в десятичную.
Решение:
2 1 0 -1 -2
1 0 1,0 1 2 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2
=4+0+1+0+0,25=5,2510
Ответ:
101,012 = 5,2510
Пример 3. Перевести число 122013 из троичной системы
счисления в десятичную.
Решение:
4 3 2 1 0
1
2 2 0 1 3=1*34 + 2*33 + 2*32
+ 0*31 + 1*30 = 81+54+18+1 = 15410
Ответ:
122013 = 15410
Пример 4. Перевести число 1637 из семеричной
системы счисления в десятичную.
Решение:
1637 = 1*72 + 6*71 + 3*70 =
49+42+3= 9410.
Ответ:
1637 = 9410.
Пример 5. Перевести число 234,68 из восьмеричной
системы в десятичную:
Решение:
2 1 0 -1
2 3 4, 68
= 2*82 +3*81 + 4*80 +6*8-1=
2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Ответ:
234,68 = 156,7510.
Пример 6. Перевести число
2Е16 в десятичную систему счисления.
Решение:
2 1
2 Е16 = 2*161 +14*160
= 32 +14 = 4610.
Ответ:
2Е16 = 4610.
Арифметические
действия с числами в различных системах счисления
Арифметические действия с числами в различных системах
счисления осуществляются практически точно так же, как и в нашей привычной
десятичной системе счисления, только надо внимательно следить в какой именно
системе счисления проводятся вычисления. От этого зависит, сколькими символами
для записи чисел мы можем оперировать. Так, например, в десятичной системе это
десять цифр (от 0 до 9), а в двоичной системе счисления – это всего два
символа, 0 и 1.
Попробуем рассмотреть все основные арифметические
действия на примере чисел в двоичной системе счисления. В остальных системах
счисления алгоритм будет тот же, главное следить, что, допустим, в восьмеричной
системе счисления переход в следующий разряд происходит при достижении 8 (т.е.
пишем 0, а 1 переходит в следующий разряд, как в десятичной происходит при
достижении 10-ти), а в шестнадцатеричной системе счисления – при достижении
16-ти.
Сложение
Для начала необходимо усвоить основные правила
сложения двоичных чисел:
02 + 02 = 02;
02 + 12 = 12;
12 + 02 = 12;
12 + 12 = 102.
Как видно, от десятичной она отличается последней
строчкой. При сложении числе «столбиком» в последнем случае будем применять
правило «0 пишем, 1 помним». В случае 12 + 12 + 12
= 102 + 12 = 112 «1 пишем, 1 помним».
Пример
Вычитание
Перейдем к чуть более сложному действию – вычитанию.
Для начала познакомимся с правилами:
02 — 02 = 02;
12 — 12 = 02;
12 — 02 = 12;
02 — 12 = -12 .
В последнем случае при выполнении вычитания
«столбиком» мы будем «занимать» десяток из старшего разряда. Помним, что
двоичный десяток равен 2.
Пример
Умножение
При умножении будем применять знакомые всем правила:
1) Любое число при умножении на 0 равно 0;
2) Любое число (кроме нуля), умноженное на
единицу, равняется самому себе.
Исходя из этого, двоичная таблица умножения будет выглядеть
так:
02 х 02 = 02;
12 х 02 = 02;
02 х 12 = 02;
12 х 12 = 12
Как видим, проще таблицу трудно представить.
Рассмотрим умножение на примере. Помимо таблицы нам еще понадобится определение
значимого числа. Все цифры, кроме ноля называются значимыми. Ноль
единственное незначимое число.
Пример: Умножим
1011002 на 10102.
При записи «столбиком» расположим числа так, чтобы
выровнять их справа по значимым цифрам:
Деление
Вспомним правила деления:
1) На ноль делить нельзя;
2) Любое число, деленное на единицу, равняется
самому себе.
Исходя из этого, двоичная таблица деления будет
выглядеть так:
02 : 02 – на ноль делить нельзя;
12 : 02 – на ноль делить нельзя;
02 : 12 = 02;
12 : 12 = 12 .
Пример: Разделим
111102 на 1102. При этом в частном будут 
Собственно говоря, арифметически действия рассмотрены.
Для более успешного усвоения полученной информации требуются навыки решения
практических заданий, получение которых и предполагается, используя следующий
раздел данного пособия.
Практикум
Перевод чисел из одной системы
счисления в другую
1.
Запишите арабскими цифрами
|
а) IV |
б) VI |
в) VIII |
|
г) IX |
д) XII |
е) XV |
|
ж) XIV |
з) XVI |
и) XIX |
|
к) XL |
л) XLII |
м) XLIV |
|
н) LIX |
о) LXIX |
п) XC |
|
р) CXIV |
с) CXXVIII |
т)CXLIX |
|
у) CDLX |
ф) DCCXVI |
х) DCCXLIV |
|
ц)CMIX |
ч)MCDXLIV |
ш) MMDCCCXCIV |
2.
Запишите римскими цифрами
|
а) 1 |
б) 3 |
в) 10 |
|
г) 50 |
д) 7 |
е) 9 |
|
ж) 12 |
з) 22 |
и) 34 |
|
к) 55 |
л) 41 |
м) 49 |
|
н) 83 |
о) 97 |
п) 101 |
|
р) 104 |
с) 119 |
т)148 |
|
у) 327 |
ф) 511 |
х) 493 |
|
ц) 1024 |
ч) 2048 |
ш) 3493 |
3.
Какое число следует за каждым
из данных? Ответ для каждого числа запишите в указанной и десятичной системах
счисления.
|
а) б) |
в) г) |
4.
Какое число предшествует
каждому из данных? Ответ для каждого числа запишите в указанной и десятичной
системах счисления.
|
а) б) |
в) г) |
5.
Переведите в десятичную
систему счисления
|
а) б) в) г) д) е) ж) з) и) к) |
л) м) н) о) п) р) с) т) у) ф) |
6.
Переведите из десятичной
системы счисления
а)
24510→А2
б)
40410→А8
в)
198710→А2
г)
67310→А16
д)
16110→А3
е)
4534810→А16
ж) 33310→А5
з)
44410→А7
и)
0, 6562510→А16
к)
0,710→А2
с точностью до 4 знаков после запятой
л)
0,412510→А8
с точностью до 6 знаков
м)
173,562510→А2
н)
404,6562510→А16
о)
125,2510→А8
7.
Переведите в двоичную
систему счисления
|
а) б) в) г) |
а) б) в) г) |
д) е) ж) з) |
и) к) л) м) |
8.
Сравните числа:
|
а) б) в) |
г) д) е) |
9.
Докажите тождества:
а)
225338 =
100101010110112
б)
10010101111002
= 12BC16
в)
101010100111002
= 252348
г)
1C6316 =
11100011000112
10.
Расположите числа,
записанные в различных системах счисления, в порядке возрастания:
а)
3510, 368,
3А16, 1001012, 1304
б)
1110012, 648,
9Е16, 2510, 2103
в)
728, 15610,
1010012, 8В16, 2325
г)
12D16, 788,
1000112, 54110, 1245
Задания на арифметические действия
1.
Выполните сложение:
|
а) б) в) г) д) е) ж) з) и) к) |
л) м) н) о) п) р) с) т) у) |
2.
Выполните вычитание:
|
а) б) в) г) д) е) ж) з) и) к) |
л) м) н) о) п) р) с) т) у) |
3.
Выполните умножение:
|
а) б) в) г) д) е) ж) з) и) к) |
л) м) н) о) п) р) с) т) у) |
4.
Выполните деление:
|
а) б) в) г) д) е) ж) з) и) |
к) л) м) н) о) п) р) с) |
5.
Решите уравнения:
|
а) б) в) г) д) е) ж) з) и) к) л) м) |
н) о) п) р) с) т) у) ф) х) ц) ч) ш)Х2 -10102 = 10102 |
Текстовые задания
1.
У меня в классе 101
ученик, из них 23 мальчика и 12 девочек. Ребята, определите, сколько в классе
учеников. Сколько мальчиков и сколько девочек .В какой системе счисления я вела
счёт?
2.
В магазин «Детский мир»
привезли игрушки: мячи и лошадки. Всего игрушек было 400 штук. Из них мячей 94
штуки, а лошадок 120 штук. Определить систему счисления, количество игрушек и сколько
было лошадок и мячей отдельно.
3.
В королевском замке жили
33 придворных дамы и 51 рыцарь. Всего их было 500 человек. Определите систему
счисления, количество дам и рыцарей, а также общее число жителей замка.
4.
В корзине лежит 400
фруктов. Из них 56 груш и 29 яблок. Определите систему счисления, количество
груш и яблок, и количество всех фруктов в корзине.
5.
В детском саду было всего
100 малышей, из них 43 девочки и 35 мальчиков. Определите систему счисления,
количество девочек и мальчиков, и количество всех малышей.
Задание на координатной плоскости
1.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
двоичной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
x |
101 |
1000 |
1001 |
1011 |
1100 |
1100 |
1011 |
1011 |
1001 |
1001 |
1010 |
1010 |
|
y |
101 |
1000 |
1000 |
110 |
110 |
111 |
111 |
10 |
10 |
11 |
11 |
100 |
|
№ точки |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
x |
111 |
111 |
101 |
101 |
110 |
110 |
111 |
111 |
10 |
10 |
11 |
11 |
100 |
|
y |
100 |
10 |
10 |
11 |
11 |
1001 |
1001 |
1000 |
1000 |
1001 |
1001 |
110 |
101 |
2.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
восьмеричной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
x |
5 |
5 |
4 |
3 |
3 |
5 |
5 |
3 |
2 |
2 |
4 |
10 |
12 |
12 |
11 |
7 |
|
y |
1 |
3 |
5 |
6 |
7 |
11 |
13 |
13 |
14 |
15 |
16 |
16 |
15 |
14 |
13 |
13 |
|
№ точки |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
|
x |
7 |
11 |
11 |
12 |
12 |
10 |
11 |
7 |
7 |
10 |
7 |
7 |
6 |
6 |
5 |
6 |
6 |
|
y |
11 |
10 |
7 |
6 |
5 |
2 |
5 |
7 |
6 |
4 |
1 |
4 |
5 |
7 |
5 |
4 |
2 |
3.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
шестнадцатеричной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
x |
7 |
5 |
5 |
3 |
1 |
3 |
4 |
7 |
9 |
B |
A |
A |
E |
11 |
F |
10 |
E |
6 |
7 |
|
y |
1 |
3 |
4 |
4 |
5 |
7 |
7 |
6 |
8 |
8 |
7 |
6 |
5 |
7 |
4 |
1 |
3 |
3 |
2 |
4.
Отметьте и
последовательно соедините на
координатной плоскости точки, координаты которых записаны в восьмеричной
системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
x |
5 |
6 |
5 |
5 |
6 |
5 |
4 |
4 |
2 |
3 |
1 |
3 |
4 |
5 |
5 |
7 |
10 |
13 |
|
y |
4 |
5 |
6 |
7 |
10 |
12 |
16 |
21 |
21 |
22 |
23 |
24 |
24 |
22 |
21 |
13 |
14 |
14 |
|
№ точки |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
x |
15 |
16 |
20 |
21 |
17 |
13 |
11 |
17 |
17 |
15 |
15 |
16 |
12 |
13 |
13 |
7 |
7 |
10 |
|
y |
13 |
11 |
10 |
5 |
2 |
2 |
3 |
3 |
4 |
6 |
5 |
4 |
4 |
5 |
6 |
6 |
5 |
4 |
5.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
двоичной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||||
|
x |
0111 |
0101 |
0101 |
0011 |
0001 |
0011 |
0100 |
0111 |
1001 |
1011 |
||||||
|
y |
0001 |
0011 |
0100 |
0100 |
0101 |
0111 |
0111 |
0110 |
1000 |
1000 |
||||||
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||||||
|
x |
1010 |
1010 |
1110 |
10001 |
1111 |
10000 |
1110 |
0110 |
0111 |
|||||||
|
y |
0111 |
0110 |
0101 |
0111 |
0100 |
0001 |
0011 |
0011 |
0011 |
|||||||
6.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
шестнадцатеричной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
x |
5 |
5 |
4 |
3 |
3 |
5 |
5 |
3 |
2 |
2 |
4 |
8 |
A |
A |
9 |
7 |
7 |
|
y |
1 |
3 |
5 |
6 |
7 |
9 |
B |
B |
C |
D |
E |
E |
D |
C |
B |
B |
9 |
|
№ точки |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
|
x |
9 |
9 |
A |
A |
8 |
9 |
7 |
7 |
8 |
7 |
7 |
6 |
6 |
5 |
6 |
6 |
|
y |
8 |
7 |
6 |
5 |
2 |
5 |
7 |
6 |
4 |
1 |
4 |
5 |
7 |
5 |
4 |
2 |
7.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
двоичной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
x |
1001 |
1000 |
1001 |
1000 |
1000 |
0111 |
0111 |
0110 |
0101 |
0101 |
0100 |
0100 |
0110 |
|
y |
0100 |
0100 |
0101 |
0110 |
1001 |
1010 |
1100 |
1011 |
1100 |
1011 |
1100 |
1101 |
1111 |
|
№ точки |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
x |
0111 |
1001 |
1010 |
1101 |
1111 |
1110 |
1111 |
1110 |
10000 |
1100 |
1011 |
1010 |
|
y |
1111 |
1101 |
1101 |
1010 |
0101 |
0110 |
0100 |
0101 |
0001 |
0100 |
0100 |
0101 |
8.
Отметьте и последовательно
соедините на координатной плоскости точки, координаты которых записаны в
двоичной системе счисления:
|
№ точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x |
0111 |
0110 |
0110 |
0101 |
0100 |
0101 |
0110 |
0110 |
0111 |
1000 |
|
y |
0010 |
0011 |
0110 |
0110 |
0111 |
1000 |
1000 |
1001 |
1000 |
0101 |
|
№ точки |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
x |
1001 |
1011 |
1101 |
1110 |
1111 |
1111 |
1110 |
10000 |
1011 |
1001 |
|
y |
0111 |
1000 |
1000 |
0111 |
0101 |
0100 |
0010 |
0001 |
0001 |
0010 |
Список использованных источников
1.
http://kuzelenkov.narod.ru/mati/book/inform/inform2.html
2.
http://comp-science.narod.ru/Progr/Syst_Sch.html
3.
http://it.school2.ochakiv.info/11class/number_systems
4.
http://fizinfo.clan.su/index/sistemy_schislenija/0-7
5.
http://www.inf1.info
6.
http://comp-science.narod.ru/KR/K_1_LR_S.html
7.
http://www.studfiles.ru/dir/cat32/subj183/file18711/view167486.html
8.
http://www.metodichka.net/?itemid=57&catid=24
9.
http://www.rusedu.info/Article882.html
10.
http://informatika.na.by/files/razrabotkiurokovimeropriiatii/scenarii/new1/new1/rfjklsa.htm
11.
http://de.ifmo.ru/bk_netra/page.php?tutindex=19&index=23
12.
http://www.gim2.ru/inf/uroki/cc.htm
13.
http://www.allinformatika.ru/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
Это ж всё брутфорс, это ж несерьезно 
На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.
350214х = 11892410
Это означает, что
3x5 + 5x4 + 0x3 + 2x2 + 1x + 4 = 11892410
или
3x5 + 5x4 + 2x2 + x – 118920 = 0
Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 
Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:
x = 8
Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 — 4.865i) 
На этой странице вы узнаете
- В каких случаях 10 не равно 10?
- Как купить шоколадку у инопланетянина?
Привычная нам система счисления называется десятичной, потому что нам с детства удобно считать 10 пальцев на руках. Но так было не всегда: раньше людям было удобнее считать до 12, по количеству фаланг на пальцах одной руки. Для них и для нас число 10 имеет совершенно разное значение.
Виды систем счисления
Система счисления — это модель, которая позволяет записывать числа по определенным правилам.
Основных типов систем счисления две:
- позиционные,
- непозиционные.
Непозиционные системы счисления основываются на том, что значение цифр никак не зависит от того, на какой позиции в числе они находятся.
Возьмем фермера и его овец. Какой способ записать количество овец — самый удобный? Самый простой пример — подсчет с помощью одной насечки. Тогда мы подсчитываем овец в своем стаде поштучно, обозначая при записи каждую отдельной засечкой.

Очевидно, что это неудобно. В наших интересах размножать овец. Но чем их больше, тем менее читаема такая запись. Когда мы добьемся невиданных высот в скотоводстве, и у нас станет 2796 голов, их подсчет с помощью одной засечки будет невозможен.
Римская система счисления — еще один известный пример непозиционной системы счисления. В ней уже появляются символы для обозначения отдельных чисел. Но в какой бы позиции символ ни стоял, он все еще значит только самого себя:
- I — 1;
- V — 5;
- X — 10 и так далее.
Римская система счисления упрощает запись чисел, но не решает проблему неудобства чтения полностью. Например, число 2796 в римской записи будет выглядеть как MMDCCXCVI. Уже неприятно.
В позиционных системах счисления значение цифры зависит от того, на какой позиции она стоит.
На примере нашей родной десятичной системы счисления, мы с вами понимаем, что в числе 1234:
- 1 — количество тысяч, и обозначает не 1, а 1000;
- 2 обозначает количество сотен и понимается как 200;
- 3 отвечает за количество десятков и означает 30;
- 4 стоит на самой последней позиции и означает количество единиц, поэтому в данном случае 4 — это 4.
Это сильно упрощает чтение чисел любого размера, так как меняется сам принцип их чтения:
- В непозиционной системе счисления (на примере римской): СХХIII = 100 + 10 + 10 + 1 + 1 + 1 = 123.
- В позиционной: 123 = 100 + 20 + 3.
Именно позиционную систему счисления выберет грамотный фермер, чтобы подсчитать количество овечек.
Основание позиционной системы счисления
Позиционная система счисления характеризуется ее основанием — количеством цифр, которые она использует для записи чисел.
- Десятичная система счисления (10сс) использует 10 цифр — от 0 до 9, с ней мы знакомы с детства.
- Компьютеру роднее двоичная система счисления (2сс), которая использует 2 цифры — 1 и 0.
- В двенадцатеричной системе счисления (12сс) помимо цифр 0–9 необходимы еще два символа. Для удобства заменим их буквами: A = 10, B = 11. Теперь имеем 12 символов от 0 до B.
- Также небезызвестная система счисления — шестнадцатеричная. Для нее кроме цифр 0–9 нужно еще больше символов, чтобы обозначить все цифры. Происходит это по аналогии — каждая новая буква отвечает за большее значение: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Мы используем числа тогда, когда кончаются цифры. Привычная нам система счисления называется десятичной, потому что использует 10 цифр — от 0 до 9. Для записи значений больше 9, мы начинаем строить числа из цифр. Первое такое число — 10.
Если бы мы использовали другое количество цифр, всё выглядело бы иначе. При использовании цифр от 0 до 6, нам пришлось бы строить числа уже для записи значений, больше 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления.
Построение числа в непривычных нам системах счисления происходит точно так же, как и в 10сс:
- Увеличиваем значения единиц, используя доступные цифры.
- Как только цифры закончились, значение единиц обнуляется. Появляется новый разряд десятков, который также увеличивается от 1 до предела системы счисления.
- Когда любой разряд числа принимает значение максимальной цифры — разряд выше увеличивается на 1, а текущий разряд обнуляется.
Например:
- В 10сс число 88 будет увеличиваться так:
88 → 89 → 90 → 91 → 92 → … 99 → 100;
- В 2сс разряды будут появляться быстрее из-за маленького количества цифр:
1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000;
- В 12сс чуть медленнее, так как цифр больше:
8 → 9 → A → B → 10 → 11 → … 18 → 19 → 1A → 1B → 20 → … 99 → 9A → 9B → A0 → A1 → … AA → AB → B0 → B1 → … BA → BB → 100.
Арифметика, как и построение числа, во всех системах счисления одинакова:
- Изменение разрядов происходит с единиц.
- При сложении избыток суммы увеличивает разряд выше (то самое “6 пишем, 1 в уме”).
- В вычитании при необходимости занимаем значение из старшего разряда, уменьшая его на 1.
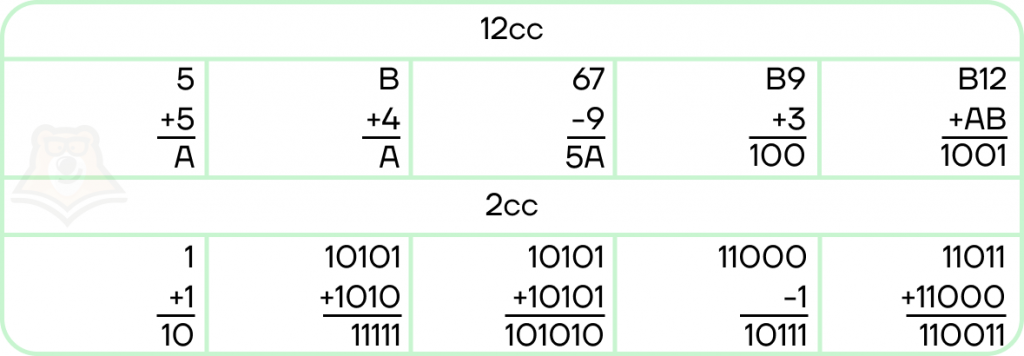
Расширенная запись числа и перевод из Nсс в 10сс
Уметь переводить числа из 10сс в другие и обратно важно для того, чтобы торговать с инопланетянами.
Однажды мы, вероятно, достучимся до внеземных цивилизаций. Но у них может оказаться не 10 пальцев на руках, а 7, 12 или любое другое количество. Если их представления о математике шли путем, подобному нашему, какую систему счисления придумали они?
Когда мы захотим купить инопланетный сникерс за 2256 межгалактических юнитов, вполне может оказаться, что наши представления о числах сильно отличаются.

Подсчитав количество пальцев на руках продавца шоколадок, важно научиться переводить числа из одной системы счисления в другую.
Полная запись числа a1a2a3…ai, где ai — цифра числа под номером i, состоящей из k символов и с основанием системы счисления n, будет выглядеть как:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
На примерах:
- 123 в 10сс расписывается как: 1 * 102 + 2 * 101 + 3 * 100;
- 1010 в 2сс: 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20;
- A9B в 12сс: 10 * 122 + 9 * 121 + 11 * 120.
Такой записи числа достаточно, чтобы перевести значение числа из любой системы счисления в 10сс — нужно посчитать значение составленной записи:
- 10102 = 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 8 + 0 +2 + 0 = 1010;
- 5259 = 5 * 92 + 2 * 91 + 5 * 90 = 5 * 81 + 2 * 9 + 5 * 1 = 42810;
- A9B12 = 10 * 122 + 9 * 121 + 11 * 120 = 10 * 144 + 9 * 12 + 11 * 1 = 155910.
Перевод из 10сс в Ncc
Принцип деления с остатком поможет переводить числа в другую сторону — из 10сс в любую другую систему счисления.
Алгоритм перевода следующий:
1. Делим исходное число на основание новой системы счисления.
2. Остаток от деления — новая найденная цифра числа.
3. Целую часть от деления снова делим на основание. Записываем остаток как новую цифру искомой записи, а целую часть от деления — как цель следующего деления. Снова делим целую часть на основание.
4. Деление происходит до тех пор, пока целая часть от деления не станет равна 0.
5. Полученные в качестве остатков от деления цифры нового числа читаются в обратном порядке.
Для примера давайте переведем число 2589 в 7сс:
- На первом шаге делим исходное число на 7, записывая остаток от деления как новую цифру и целую часть как оставшееся значение.

- На втором шаге делаем то же самое, но с целой частью предыдущего деления — теперь делим ее на 7.

- И так до тех пор, пока целая часть от деления не будет равна 0.



Интересующее нас значение находится в самом правом столбце и читается снизу вверх.
258910 = 103567
Перевод в системы счисления с основанием, больше 10, происходит так же. Просто надо не забывать, что цифры больше 9, будут обозначаться соответствующими буквами.
Например, таблица перевода десятичного числа 48406 в 16сс будет выглядеть следующим образом:

И искомое значение будет BD16.
Лайфхак или как быстрее закодировать геном
Представим, что нам нужно написать программу для биологов, которую они будут применять в исследованиях ДНК и нам надо реализовать хранение ДНК в памяти компьютера.
В ДНК встречается четыре вида азотистых оснований: аденин (A), гуанин (G), тимин (T) и цитозин (C). Всю ДНК можно записать как последовательность этих 4 символов. Но можно же записать тогда эту последовательность букв как число в 4сс, сопоставив цифры символам, например, код A – 0, C – 1, G – 2, T – 3. Тогда кусок ДНК GGT будет записан в 4сс как 223.
Но чтобы закодировать геном в компьютере, его надо перевести из 4сс в 2сс. Делать это делением может оказаться очень долго, ведь геном может быть очень длинным и делить его просто неэффективно. К счастью, есть выход!
Между 2сс и системами счисления, в основании которых стоит степень двойки (4сс, 8сс, 16сс), есть связь, которую можно использовать для быстрого перевода из 2сс в них и обратно. Для этого используется следующая таблица:
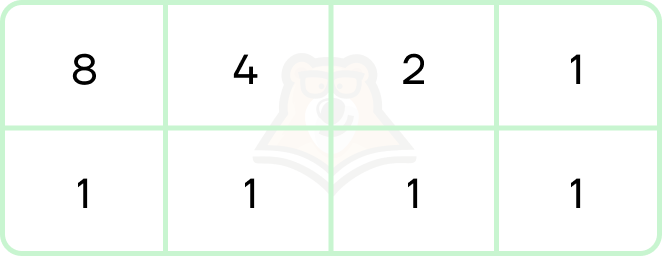
Алгоритм перевода состоит в следующем:
1. Вычисляется степень, в которую нужно возвести 2, чтобы получить основание необходимой системы счисления.
2. Используется количество столбцов таблицы, равное этой степени. Отсчет ведем с правого столбца.
3. При переводе из 2сс весь код разбивается на кодовые слова длиной, равной степени — при необходимости в начало записи добавляются нули. Отдельные кодовые слова подставляются в нижнюю строку таблицы. Цифра записи числа в новой системе счисления будет равна сумме цифр верхней строки, под которыми стоит 1 кодового слова.
4. При переводе в 2сс каждая цифра представляется как сумма цифр верхней строки таблицы. Цифрам, которые используются в сумме, соответствуют 1 кодового слова 2сс, а не использующимся — 0.
На примере:
- Для перевода между 2сс и 4сс используется часть таблицы:
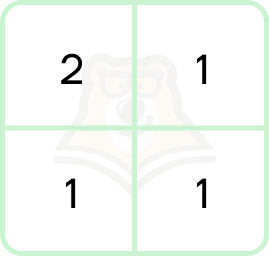
- Перевод из 2сс в 4сс:
110001 = 11.00.01 = (2 + 1).(0 + 0).(0 + 1) = 3.0.1 = 301
- Перевод из 4сс в 2сс:
103 = 1.0.3 = (0 + 1).(0 + 0).(2 + 1) = 01.00.11 = 10011
- Для перевода между 2сс и 8сс используется часть таблицы:
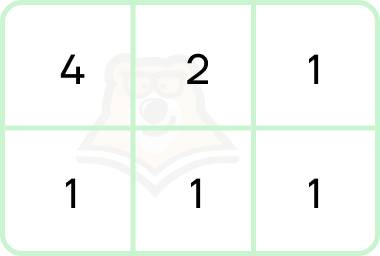
- Перевод из 2сс в 8сс:
10101011100 = 010.101.011.100 = (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1).(4 + 0 + 0) = 2.5.3.4 = 2534
- Перевод из 8сс в 2сс:
1753 = 1.7.5.3 = (0 + 0 + 1).(4 + 2 + 1).(4 + 0 + 1).(0 + 2 + 1) = 001.111.101.011 = 1111101011
- Для перевода между 2сс и 16сс используется вся таблица:
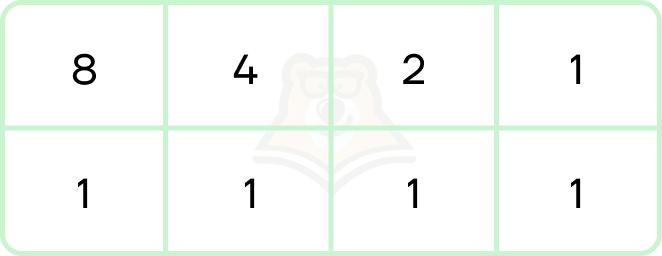
- Перевод из 2сс в 16сс:
101101111000001 = 0101.1011.1100.0001 = (0 + 4 + 0 + 1).(8 + 0 + 2 + 1).(8 + 4 + 0 + 0).(0 + 0 + 0 + 1) = 5.11.12.1 = 5BC1
- Перевод из 16сс в 2сс:
F87A = 15.8.7.10 = (8 + 4 + 2 + 1).(8 + 0 + 0 + 0).(0 + 4 + 2 + 1).(8 + 0 + 2 + 0) = 1111.1000.0111.1010 = 1111100001111010
Перевод между системами счисления на Python
Перевод больших чисел между системами счисления вручную неудобен и может занимать много времени. Иногда выгоднее было бы написать программу.
Перевод из 10сс в другие будем выполнять по описанному выше алгоритму. Пока исходное число больше 0, делим его на основание системы счисления. Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.
- Основным циклом программы будет while, который работает, пока исходное число больше 0.
- Новую цифру числа берем как остаток от деления исходного числа на основание новой системы счисления с помощью оператора %. Новые цифры будем записывать в новую строку, в которой и будет храниться искомая запись. Чтобы не переворачивать число в конце, можем сразу заносить каждую новую цифру не в конец, а в начало строки.
- Уменьшаем само число, деля его нацело на основание с помощью оператора //.
Например, перевод числа 258936 в 5сс.
number = 258936
n = 5
new_number = ""
while number > 0:
d = number % n
new_number = str(d) + new_number
number //= n
print(new_number)
_____________________________________________________________________
Вывод: 31241221Перевод в 10сс из других систем счисления будем производить по описанной выше формуле:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
- Главный цикл программы — for. Он будет перебирать цифры исходного числа, а точнее, их индексы, с помощью диапазона range по длине исходного числа.
- На каждом шаге цикла цифру ai числа будем умножать на основание системы счисления этого числа n в степени, равной разности длины числа k и порядкового номера текущей цифры i — ai*nk — i . Не забываем, что индексация строки начинается с 0, а не с 1, поэтому порядковый номер цифры — на 1 больше ее индекса.
Например, переведем число 31241221 из 5сс обратно в 10сс.
number = "31241221"
n = 5
new_number = 0
k = len(number)
for i in range(k):
new_number += int(number[i]) * n ** (k - i - 1)
print(new_number)
_____________________________________________________________________
Вывод: 258936Лайфхаки по переводу между системами счисления программой:
- для перевода числа из 10сс в 2сс, 8сс и 16сс есть встроенные команды: bin, oct и hex соответственно
- bin(123) — “0b1111011”
- oct(123) — “0o173”
- hex(123) — “0x7b”
Важно заметить, что первые два символа в записи числа окажутся лишними в нашем случае — они будут обозначать идентификатор системы счисления, в которую мы перевели число.
Чтобы сразу от него избавиться, при переводе можно использовать срез, который будет учитывать все число без этого идентификатора:
- bin(123)[2:] — “1111011”
- oct(123)[2:] — “173”
- hex(123)[2:] — “7b”
- перевести число из любой системы счисления в 10сс можно с помощью команды int. Ей необходимо передать два параметра: исходное число в виде строки и основание его системы счисления:
- int(«31241221», 5) — 258936
- int(«7b», 16) — 123
Хорошо. А зачем всё это, если мы не генетики и не торгуем с инопланетянами?
Системы счисления — одно из базовых понятий информатики и оттого используются в большом количестве заданий на ЕГЭ. С применением различных систем счисления придется столкнуться при решении задачи 14, при построении большинства алгоритмов задачи 5, в заданиях на расчет объема информации в номере 7. Также, хотя это не упоминается в условиях заданий явно, в задаче 22 немалая часть алгоритмов связана с переводом числа из одной системы в другую.
Фактчек
- В позиционных системах счисления, в отличие от непозиционных, значение цифры зависит от ее положения в числе.
- Основание позиционной системы счисления определяет количество используемых в ней цифр для записи чисел.
- Для перевода из 10сс в любую другую: берем остаток от деления на основание новой системы счисления в качестве цифр нового числа и записываем их в обратном порядке.
- Для перевода из любой системы счисления в 10сс: умножаем каждую цифру числа на основание его системы счисления, возведенную в степень разности длины числа и порядкового номера данной цифры.
Проверь себя
Задание 1.
Какая цифра не может использоваться в 8сс?
- 0
- 3
- 7
- 8
Задание 2.
Для записи цифр 10-15 в 16сс используются …
- буквы A-F
- буквы А-Д
- буквы U-Z
- любые символы по договоренности
Задание 3.
Десятичное число 101 в 2сс будет выглядеть как…
- 101
- 101101
- 1100101
- 1010011
Задание 4.
Шестнадцатеричное число FBA000 в 10сс будет выглядеть как …
- 16490496
- 69409461
- 61400900
- Это некорректная запись числа в 16сс
Задание 5.
Что сделает запись на языке Python — int(“777”, 8)?
- Переведет число 777 из 10сс в 8сс
- Переведет число 8 из 10сс в 777сс
- Переведет число 777 из 8сс в 10сс
Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.