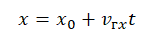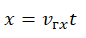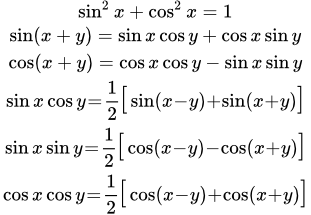Часто задаваемые вопросы как найти ускорение с учетом угла и коэффициента кинетического трения. В системе ускорения коэффициент трения является одним из основных факторов.
Ускорение в движущейся системе может быть разных форм. Например, в наклонной плоскости мы должны учитывать угол, под которым движется тело. Итак, учитывая все эти атрибуты, мы будем иметь дело с факторами, в основном ответственными за ускорение тела.
Когда наклон имеет тело или любой объект, который находится в постоянном движении, он будет рассчитываться в соответствии с поднятой проблемой. Здесь мы обсудим, как найти ускорение с углом и коэффициентом кинетического трения.
Мы должны знать, как нас ускоряют в движущейся машине. Когда машина движется с определенной скоростью, мы, как правило, возвращаемся на сиденье, когда скорость повышается. Когда в машине применяются тормоза, мы стремимся двигаться вперед, а на поворотах мы склонны двигаться боком. Это способы ускорения.
Ускорению способствуют несколько различных факторов. В одном из них нам нужно сосредоточиться на данных деталях. Здесь мы будем иметь дело с коэффициентом трения и углом, под которым он будет ускоряться.
Подробная информация о коэффициенте трения и его влиянии на ускорение
Коэффициент трения — это, по сути, наименьший фактор, влияющий на ускорение любого объекта, который уже находится в движении. Он основан на силах, действующих на тело, находящееся в постоянном движении.
Во-первых, это сила тяжести, одна из основных причин, по которой тело оказывается на земле без какой-либо левитации. Далее будет нормальная сила, действующая на тело. Эта нормальная сила — это сила, исходящая от окружающей среды. Далее идет сила трения, которая в основном отвечает за то, чтобы тело действительно могло совершать любые движения.
Нормальная сила и сила трения являются одними из основных факторов ускорения. Когда тело движется с определенной скоростью, внезапно набирает скорость и движется с другой скоростью, это называется ускорением.
На самом деле мы должны были знать, как это трение влияет на ускорение и как работает коэффициент трения при ускорении. Когда тело находится в процессе ускорения, в игру вступают несколько аспектов.
На тело в движении действует так много сил. В этой системе ускорения мы должны найти силы, присутствующие и действующие на это тело. Затем нам нужно соответственно рассчитать ускорение.
Сосредоточение внимания на силе трения является одним из факторов, влияющих на движение тела по земле. Например, автомобиль движется из-за трения между шиной автомобиля и дорогой, или в данном случае это может быть любая поверхность.
Как найти ускорение по углу и коэффициенту кинетического трения
Здесь нам нужно рассмотреть столько же примеров, как найти ускорение с учетом угла и коэффициента кинетического трения. Сначала идет угол, затем коэффициент трение. От угла болота зависит, как тело движется по наклонной плоскости.
Теперь рассмотрим случай, когда объект помещен на поверхность, ниже которой он фактически наклонен. Теперь по каким-то причинам объект теряет равновесие и скатывается по наклонной поверхности. Следовательно, необходимо оценить ускорение тела, движущегося в наклонной плоскости.
В этом сценарии сила трения кинетическая, она действует противоположно силе тяжести. Чистая сила также должна быть рассчитана. Нам нужно определить чистую силу, чтобы найти ускорение тела с учетом угла и коэффициента трения.
F = Fg + Fk; F = мг (синус θ) + мкг (cos θ)
Мы знаем, что ускорение — это [сила, деленная на массу, следовательно, a = F / m. Следовательно, из формулы чистой силы мы получаем ускорение как а = g (синус θ) + μ g (cos θ).
Используя эту формулу, мы можем найти ускорение с коэффициентом трения с углом, под которым он движется.
Задача о том, как найти ускорение с учетом угла и коэффициента кинетического трения
1 задачи:
Допустим, автомобиль весом 1200 кг движется по неровной дороге. Значение коэффициента трения равно 0.8. Fnet = 7000N будет расчетной чистой силой, действующей на это движущееся тело. Теперь первое, что нужно оценить, — это ускорение данной конкретной системы.
Решение 1:
Поскольку дана результирующая сила, мы можем найти нормальную силу, используя значение массы и силы тяжести, поскольку сила тяжести и нормальная сила равны друг другу, но действуют в разных направлениях. Сила трения находится с помощью коэффициент величины трения и значения нормальной силы.
м = 1200; Fnet = 7000N; μ = 0.8
Нормальная сила = сила тяжести x масса тела
Fn = 9.8 х 1200; Fn = 11270
Сила трения = μ x нормальная сила; Ff = 0.8x 11270 = 9016 Н
а = ф / м
а = 9016 / 1200
a = 7.51 мс-2
2 задачи:
Как найти ускорение, если задан коэффициент трения и угол наклона.
Итак, в задаче указаны коэффициент трения и угол, под которым он движется. Масса 100 кг движется вниз в наклонной плоскости под углом θ = 45⁰. Коэффициент трения μ = 0.9.
С каким ускорением тело движется вниз?
Решение 2:
Коэффициент силы, действующей на плоскости, равен mgSinθ, а коэффициент, перпендикулярный плоскости, равен mgCosθ. И мы знаем, что f = ma, поэтому a = f / m. исходя из этого, мы можем использовать значение коэффициента трения или нет.
Таким образом, мы получаем формулу как a = μgCosθ
а = 0.9 × 9.8 × 0.52
a = 4.58 мс-2.
Часто задаваемые вопросы
Как найти ускорение с трением и под углом?
Трение — единственная причина, по которой тело перемещается в любом направлении, и когда движение происходит под наклоном, угол будет учитываться.
Формула для определения ускорения с трением, а также угла: a = μgCosθ. Нам нужно знать, что действующие силы будут двух типов: одна будет соответствовать уклону, а другая сила будет перпендикулярна наклону.
Как найти ускорение по чистой силе и массе?
Масса и сила имеют прямое воздействие на тело, независимо от того, находится оно в движении или нет. Таким образом, масса и сила будут основными причинами движения конкретного тела.
Когда тело находится в движении, частью движения будет несколько различных факторов. В одном из таких случаев сила будет иметь большое влияние. Основная сила, действующая на движущееся тело, будет силой тяжести и нормальной силой, которая будет действовать перпендикулярно направлению движения. числовые силы, действующие на эту конкретную систему, должны быть найдены и затем оценены.
Масса имеет прямое воздействие на тело, поскольку это основная причина, по которой тело движется; когда масса тела увеличивается, ускорение уменьшается. Когда масса тела уменьшается, ускорение увеличивается, поэтому действующая сила больше, и телу будет легче двигаться, если только масса будет больше. Таким образом, формула ускорения с чистой силой и массой дается как a = f / m.
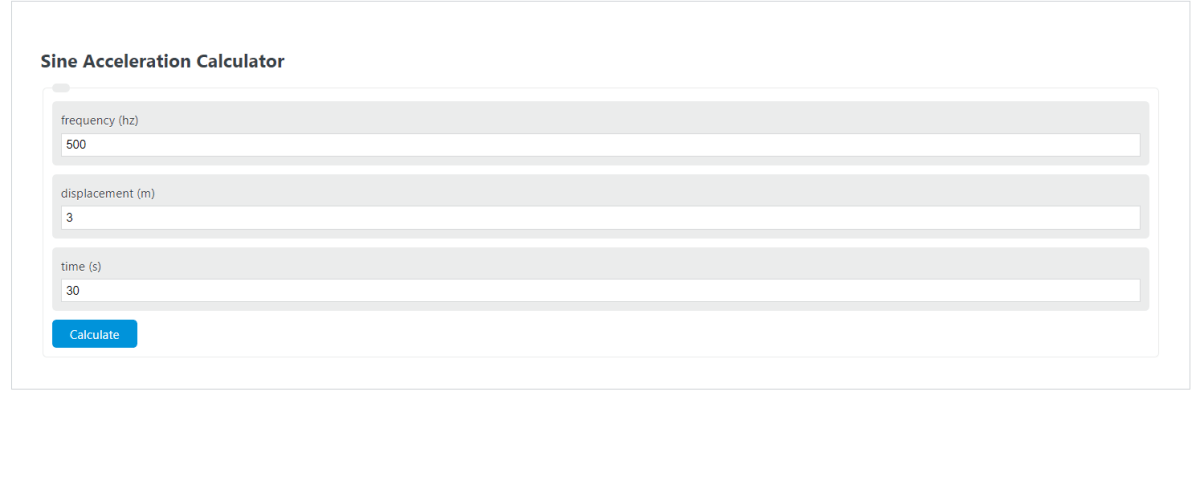
Enter the frequency, the displacement, and the time into the calculator to determine the Sine Acceleration.
- All Acceleration Calculators
- Maximum Acceleration Calculator
- Frequency Displacement Acceleration Calculator
- Frequency To Angular Velocity Calculator
- Amplitude to Acceleration Calculator
Sine Acceleration Formula
The following equation is used to calculate the Sine Acceleration.
a = -2*pi*f^2*D*sin(2*pi*f*t)
- Where a is the Sine Acceleration (m/s^2)
- f is the frequency (hz)
- D is the displacement (m)
- t is the time (s)
What are the units for Sine Acceleration?
The most common units for Sine Acceleration are m/s^2.
How to Calculate Sine Acceleration?
Example Problem:
The following example problem outlines the steps and information needed to calculate the Sine Acceleration.
First, determine the frequency. In this example, the frequency is determined to be 500 (hz).
Next, determine the displacement. For this problem, the displacement is measured to be 3 (m).
Next, determine the time. In this case, the time is found to be 30 (s).
Finally, calculate the Sine Acceleration using the formula above:
a = -2*pi*f^2*D*sin(2*pi*f*t)
Inserting the values from above and solving the equation with the imputed values gives:
a = -2*3.14159*500^2*3*sin(2*3.1415*500*30) =1668802.81 (m/s^2)
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Перемещение при равноускоренном движении. Уравнение координаты
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении».
Уравнение координаты при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Уравнение координаты — зависимость координаты тела от времени:
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:
Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Аналитический способ решения задачи на совместное движение тел
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение тел
Существует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
в)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 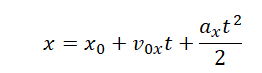
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
pазбирался: Алиса Никитина | обсудить разбор | оценить
http://interneturok.ru/lesson/physics/10-klass/mehanikakinematika/peremeschenie-pri-ravnouskorennom-dvizhenii-uravnenie-koordinaty
Уравнение координаты при равноускоренном прямолинейном движении
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Геометрическое определение синуса и косинуса
Синус ( sin α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус ( cos α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
Графики функций синус, y = sin x , и косинус, y = cos x
Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице ( n — целое).
источники:
http://epmat.ru/modul-geometriya/urok-1-trigonometriya/
http://1cov-edu.ru/mat_analiz/funktsii/sinus/