Ниже представлены таблицы с формулами степеней (квадрат, куб, в 4-ой степени) прямых и обратных тригонометрических функций: синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Содержание
скрыть
- Формулы квадратов
- Формулы кубов
- Формулы функций в 4-ой степени
Формулы квадратов
| Степень | Формула |
| Синус в квадрате |  |
 |
|
| Косинус в квадрате |  |
 |
|
| Тангенс в квадрате |  |
| Котангенс в квадрате |  |
microexcel.ru
Формулы кубов
| Степень | Формула |
| Синус в кубе |  |
| Косинус в кубе |  |
| Тангенс в кубе |  |
| Котангенс в кубе |  |
microexcel.ru
| Степень | Формула |
| Синус в 4-ой степени |  |
| Косинус в 4-ой степени |  |
| Тангенс в 4-ой степени |  |
| Котангенс в 4-ой степени |  |
microexcel.ru
n. Правила понижения степени
Из приведенного материала Ви научитесь вычислять интегралы от произведения тригонометрических выражений, которые возведены до определенного степеня. С виду они достаточно сложные
но зная правила понижения степени подынтегральной функций их решение очень просто, в чем Вы скоро убедитесь. Существует три правила понижения степени, основанные на четности или нечетности показателей.
Правила понижения степени
I. Если хотя бы один из показателей степени подынтегральной функции является нечетным числом, например то ее можно превратить к следующему виду:
В таких случаях применяют подстановку
При этом выходной интеграл примет вид
Решение сводится к интегрированию суммы степенных функций.
Если , то преобразование будет следующим
С конечного выражения видим, что замена будет другой
Начальный интеграл запишется в следующей форме
Опять получаем сумму интегралов.
II. Если оба показателя — четные числа, то используют подстановку, которая заимствовано из тригонометрии
Применение данных формул позволяет снизить степень подынтегральной функции, однако при больших значениях степеней по данному правилу несколько больше вычислений, чем за первым.
ІІІ. Показатели нечетные числа. В таких случаев используют следующую тригонометрическую равенство чтобы снизить степень
Дальнейшее интегрирование сводится к использованию второго правила. Стоит отметить, что правило хорошо тем, что в подынтегральной функции получаем только парные аргументы
На этом правила заканчиваются и пора переходить к практическим вычислениям.
Пример 1.
Вычислить интегралы
а)
б)
в)
Решение.
а) Применим к подынтегральной функции первое правило. При подстановке
подынтегральная функция примет вид
Интегрируя полученную функцию получим значение
Возвращаемся к использованной замене переменных и меняем обратно Интеграл можно переписать в конечном виде
б) К подынтегральной функции применим замену
и преобразуем к следующему виду
Выполним интегрирование
Возвращаясь к предыдущей переменной, интеграл будет иметь вид
в) Для этого интеграла нужно применять второе правило.
Проведем интегрирование каждого из слагаемых
Подытожим слагаемые, сгруппировав предварительно подобные
————————————————
Подобных примеров в интернете и литературе очень много. Правила понижения степени для всех остаются одинаковыми, потому хорошо выучите в каких случаях их применять. Все остальное сведется к интегрированию, с которым у Вас при вычислении не должно возникать проблем.
Возведение в степень
Для
возведения в степень используют функцию
СТЕПЕНЬ.
Синтаксис
функции
СТЕПЕНЬ(А;В),
где
А
— число, возводимое в степень;
В
— показатель степени, в которую возводится
число.
Отрицательные
числа можно возводить только в степень,
значение которой является целым числом.
В остальном ограничений на возведение
в степень нет.
Для
извлечения квадратного корня можно
использовать функцию КОРЕНЬ.
Синтаксис
функции
КОРЕНЬ(А),
где
А
— число, из которого извлекают квадратный
корень.
Нельзя
извлекать корень из отрицательных
чисел.
Тригонометрические вычисления
В
Microsoft Excel можно выполнять как прямые,
так и обратные тригонометрические
вычисления, то есть, зная значение угла,
находить значения тригонометрических
функций или, зная значение функции,
находить значение угла.
Синтаксис
всех прямых тригонометрических функций
одинаков. Например, синтаксис функции
SIN
SIN(А),
где
А
— угол в радианах, для которого определяется
синус.
Точно
так же одинаков и синтаксис всех обратных
тригонометрических функций.
синтаксис функции АSIN
АSIN(А),
где
А
— число, равное синусу определяемого
угла.
Следует
обратить внимание, что все тригонометрические
вычисления производятся для углов,
измеряемых в радианах. Для перевода в
более привычные градусы следует
использовать функции преобразования
(
ГРАДУСЫ,
РАДИАНЫ)
или самостоятельно переводить значения,
используя функцию ПИ().
Функция
ПИ()
вставляет значение числа
(пи).
Аргументов функция не имеет, но скобки
после названия удалять нельзя.
Например,
при необходимости рассчитать значение
синуса угла, указанного в градусах,
необходимо его умножить на ПИ()/180.
Рис.5.
Вычисление тригонометрических функций
для углов, указанных в градусах
Преобразование чисел
Преобразование
чисел может потребоваться при переводе
углов из градусов в радианы и обратно,
при определении абсолютной величины
числа, при преобразовании арабских цифр
в римские.
Для
перевода значения угла, указанного в
радианах, в градусы используют функцию
ГРАДУСЫ.
Синтаксис
функции
ГРАДУСЫ(А),
где
А
— угол в радианах, преобразуемый в
градусы.
Для
перевода значения угла, указанного в
градусах, в радианы используют функцию
РАДИАНЫ.
Синтаксис
функции
РАДИАНЫ(А),
где
А
— угол в градусах, преобразуемый в
радианы.
Функции
ГРАДУСЫ
и РАДИАНЫ
удобно использовать с тригонометрическими
функциями. Например, при необходимости
можно рассчитать значение синуса угла,
указанного в градусах (рис.
6).
Рис.
6. Вычисление
тригонометрических функций с использованием
функций «ГРАДУСЫ» и «РАДИАНЫ»
Комбинаторика
Для
расчета числа возможных комбинаций
(групп) из заданного числа элементов
используют функцию ЧИСЛКОМБ.
Синтаксис
функции
ЧИСЛКОМБ(А;
В),
где
А
— число элементов;
В
— число объектов в каждой комбинации.
Во
вспомогательных расчетах в комбинаторике
может потребоваться расчет факториала
числа. Факториал числа — это произведение
всех чисел от 1 до числа, для которого
определяется факториал. Например,
факториал числа 6 (6!) равен 1*2*3*4*5*6. Для
расчета факториала используют функцию
ФАКТР.
Синтаксис
функции
ФАКТР(А),
где
А
— число, для которого рассчитывается
факториал.
Факториал
нельзя рассчитать для отрицательных
чисел. Факториал числа 0 (ноль) равен 1.
При расчете факториала дробных чисел
десятичные дроби отбрасываются.
тригонометрия — энная степень синуса как суммы синусов и косинусов
Задай вопрос
спросил
4 года 5 месяцев назад
Изменено
4 года, 5 месяцев назад
Просмотрено
1к раз
$begingroup$
9{frac{n-2k-1}{2}}sin((n-2k)x)right]$$
У меня есть три вопроса относительно этих рядов:
- Правы ли они, даже с такой странной силой для знака минус и отдельным первым членом для четных степеней?
- Если возможно, как можно упростить эти суммы?
- Как доказать правильность этих сумм или как показать, что они неверны?
- тригонометрия
- степенной ряд
- ряд Фурье 9{-5}\=2isin5x-2icdot5sin3x+2icdot10sin x.
$$
Итак, для постоянного множителя мощность синуса представляет собой линейную комбинацию косинусов или синусов аргумента умноженное на каждое другое целое число, взвешенное по каждому другому биномиальному коэффициенту и с чередующимися знаками.
$endgroup$
6
$begingroup$
Чтобы собрать все в один пост:
Правильные суммы должны быть следующими 9ksin((n-2k)x)right]$$
где $n=2m+1$Прав ли я на этот раз или где-то ошибся?
Поскольку в сумме четных степеней все еще есть этот странный постоянный член, который меня немного раздражает.$endgroup$
интегрирование — Определенный интеграл от произведения степеней синуса и косинуса
Здесь ответ не только для высших степеней $sin x$ и $cos x,$
но действительно для
любых неотрицательных целых степеней $sin x$ и $cos x.
Понижение степени в тригонометрии
Формулы понижения степени позволяют выразить тригонометрическую функцию n-ной степени через синус и косинус первой степени кратного значению n угла.
Применяемые формулы, доказательства
Формулы понижения степени выводятся из формул двойных, тройных и т.д. углов, которые в свою очередь являются следствием формул сложения и вычитания аргументов (метод заключается в представлении данных тождеств в виде суммы двух равных углов).
Формула понижения степени синуса и косинуса
Общий вид формул понижения степени для синуса и косинуса отличается для четных и нечетных степеней. Для четных (n = 2, 4, 6, …) они выглядят следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(sin^nleft(alpharight)=frac{mathrm C_frac n2^n}{2^n}+frac1{2^{n-1}}cdotsum_{k=0}^{{textstylefrac n2}-1}{(-1)}^{{textstylefrac n2}-k}cdotmathrm C_k^ncdotcosleft((n-2k)alpharight))
(cos^nleft(alpharight)=frac{mathrm C_frac n2^n}{2^n}+frac1{2^{n-1}}cdotsum_{k=0}^{{textstylefrac n2}-1}mathrm C_k^ncdotcosleft((n-2k)alpharight))
Для нечетных степеней (n = 3, 5, 7, …) в общем виде формулы записываются так:
(sin^nleft(alpharight)=frac1{2^{n-1}}cdotsum_{k=0}^{textstylefrac{n-1}2}{(-1)}^{{textstylefrac{n-1}2}-k}cdotmathrm C_k^ncdotsinleft((n-2k)alpharight))
(cos^nleft(alpharight)=frac1{2^{n-1}}cdotsum_{k=0}^{textstylefrac{n-1}2}mathrm C_k^ncdotcosleft((n-2k)alpharight))
На практике чаще всего используются формулы для второй степени, немного реже — для третьей и четвертой. Выглядят они так:
(sin^2left(alpharight)=frac{1-cosleft(2alpharight)}2)
(cos^2left(alpharight)=frac{1+cosleft(2alpharight)}2)
(sin^3left(alpharight)=frac{3sinleft(alpharight)-sinleft(3alpharight)}4)
(cos^3left(alpharight)=frac{3cosleft(alpharight)+cosleft(3alpharight)}4)
(sin^4left(alpharight)=frac{3-4cosleft(2alpharight)+cosleft(4alpharight)}8)
(cos^4left(alpharight)=frac{3+4cosleft(2alpharight)+cosleft(4alpharight)}8)
Понижение степени тангенса и котангенса
Формулы понижения степени для тангенса и котангенса выводятся исходя из определения этих тригонометрических функций. Тангенс — частное при делении синуса на косинус, котангенс — наоборот. Готовые формулы имеют следующий вид:
(tg^2left(alpharight)=frac{1-cosleft(2alpharight)}{1+cosleft(2alpharight)})
(ctg^2left(alpharight)=frac{1+cosleft(2alpharight)}{1-cosleft(2alpharight)})
(tg^3left(alpharight)=frac{3sinleft(alpharight)-sinleft(3alpharight)}{3cosleft(alpharight)+cosleft(3alpharight)})
(ctg^3left(alpharight)=frac{3cosleft(alpharight)+cosleft(3alpharight)}{3sinleft(alpharight)-sinleft(3alpharight)})
(tg^4left(alpharight)=frac{3-4cosleft(2alpharight)+cosleft(4alpharight)}{3+4cosleft(2alpharight)+cosleft(4alpharight)})
(сtg^4left(alpharight)=frac{3+4cosleft(2alpharight)+cosleft(4alpharight)}{3-4cosleft(2alpharight)+cosleft(4alpharight)})
Понижать можно любую степень, но с ее увеличением будет расти уровень сложности выражений, получаемых в результате этого действия.
Формулы половинного угла
Несмотря на то, что данные выражения абсолютно самостоятельны и выделяются в отдельный блок, при определенной записи их также можно отнести к формулам понижения степени.
(sin^2left(fracalpha2right)=frac{1-cosleft(alpharight)}2)
(x = {-b pm sqrt{b^2-4ac} over 2a}acos^2left(fracalpha2right)=frac{1+cosleft(alpharight)}2)
(tg^2left(fracalpha2right)=frac{1-cosleft(alpharight)}{1+cosleft(alpharight)})
(ctg^2left(fracalpha2right)=frac{1+cosleft(alpharight)}{1-cosleft(alpharight)})
Вывод формул понижения степени
Рассмотрим доказательства тождеств для синуса и косинуса второй степени. Для вывода потребуются формулы двойного угла:
(cosleft(2alpharight)=2cos^2left(alpharight)-1)
(cosleft(2alpharight)=1-2sin^2left(alpharight))
Чтобы получить значение косинуса во второй степени, переносим (2cos^2left(alpharight)) в левую часть, (cosleft(2alpharight)) — в правую, и избавляемся от минуса. Получаем:
(2cos^2left(alpharight)=cosleft(2alpharight)+1)
Делим обе части уравнения на 2. В итоге остается готовая формула понижения степени для косинуса:
(cos^2left(alpharight)=frac{1+cosleft(2alpharight)}2)
Для синуса алгоритм действий точно такой же. (2sin^2left(alpharight)) переносится в левую часть уравнения, (cosleft(2alpharight)) — в правую. Делим получившееся тождество (2sin^2left(alpharight)=1-cosleft(2alpharight)) на 2 и в результате остается формула понижения степени для синуса:
(sin^2left(alpharight)=frac{1-cosleft(2alpharight)}2)
Как выполняется, примеры задач с решением
Формулы понижения степени находят свое применение в тригонометрии, при решении дифференциальных уравнений и вычислении интегралов. Рассмотрим несколько примеров их использования:
Пример 1. Вычислить значение (2cdotsin^2left(fracpi4right))
Применим формулу понижения степени для синуса в квадрате (sin^2left(alpharight)=frac{1-cosleft(2alpharight)}2). Получим следующее:
(2cdotsin^2left(fracpi4right)=frac{2cdot(1-cosleft(2cdot{displaystylefracpi4}right))}2=1-cosleft(fracpi2right))
Так как (cosleft(fracpi2right)), он же (cosleft(90^circright)) равняется 0, получим (2cdotsin^2left(fracpi4right)=1).
Пример 2. Вычислить значение интеграла (int2cos^2left(xright)d2x)
Для того, чтобы привести к одному виду значения переменных в косинусе и дифференциале, воспользуемся формулой понижения степени:
(int2cos^2left(xright)d2x=int2cdotfrac{1+cosleft(2xright)}2d2x=int1+cosleft(2xright)d2x)
Так как выражение под знаком интеграла является многочленом, проинтегрируем каждую его часть по очереди:
(int1+cosleft(2xright)d2x=int1d2x+intcosleft(2xright)d2x=x+sinleft(2xright)+mathrm C)
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin{array}{|l|l|}
hline sin^2 alpha+cos^2 alpha =1& mathrm{tg}, alpha cdot
mathrm{ctg}, alpha =1 \
&(sinalphane 0, cosalphane 0)\[0.5ex]
hline &\
mathrm{tg}, alpha=dfrac{sin alpha}{cos alpha}
&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha} \&\
1+mathrm{tg}^2, alpha =dfrac1{cos^2 alpha} & 1+mathrm{ctg}^2, alpha=dfrac1{sin^2 alpha}\&\
(cosalphane 0)& (sinalphane 0) \
hline
end{array}]
(blacktriangleright) Формулы сложения углов: [begin{array}{|l|r|}
hline &\
sin{(alphapm beta)}=sinalphacdot cosbetapm sinbetacdot
cosalpha & cos{(alphapm beta)}=cosalphacdot cosbeta mp
sinalphacdot sinbeta\ &\
hline &\
mathrm{tg}, (alphapm beta)=dfrac{mathrm{tg}, alphapm
mathrm{tg}, beta}{1 mp mathrm{tg}, alphacdot
mathrm{tg}, beta} & mathrm{ctg}, (alphapmbeta)=-dfrac{1mp mathrm{ctg}, alphacdot mathrm{ctg}, beta}{mathrm{ctg}, alphapm mathrm{ctg}, beta}\&\
cosalphacosbetane 0&sinalphasinbetane 0\
hline
end{array}]
(blacktriangleright) Формулы двойного и тройного углов: [begin{array}{|lc|cr|}
hline sin {2alpha}=2sin alphacos alpha & qquad &qquad & cos{2alpha}=cos^2alpha -sin^2alpha\
sin alphacos alpha =dfrac12sin {2alpha} && & cos{2alpha}=2cos^2alpha -1\
& & & cos{2alpha}=1-2sin^2 alpha\
hline &&&\
mathrm{tg}, 2alpha = dfrac{2mathrm{tg},
alpha}{1-mathrm{tg}^2, alpha} && & mathrm{ctg}, 2alpha
= dfrac{mathrm{ctg}^2, alpha-1}{2mathrm{ctg}, alpha}\&&&\
cosalphane 0, cos2alphane 0 &&& sinalphane 0,
sin2alphane 0\
hline &&&\
sin {3alpha}=3sin alpha -4sin^3alpha && &
cos{3alpha}=4cos^3alpha -3cos alpha\&&&\
hline
end{array}]
(blacktriangleright) Формулы понижения степени: [begin{array}{|lc|cr|}
hline &&&\
sin^2alpha=dfrac{1-cos{2alpha}}2 &&&
cos^2alpha=dfrac{1+cos{2alpha}}2\&&&\
hline
end{array}]
(blacktriangleright) Формулы произведения функций: [begin{array}{|c|}
hline \
sinalphasinbeta=dfrac12bigg(cos{(alpha-beta)}-cos{(alpha+beta)}bigg)\\
cosalphacosbeta=dfrac12bigg(cos{(alpha-beta)}+cos{(alpha+beta)}bigg)\\
sinalphacosbeta=dfrac12bigg(sin{(alpha-beta)}+sin{(alpha+beta)}bigg)\\
hline
end{array}]
(blacktriangleright) Формулы суммы/разности функций: [begin{array}{|lc|cr|}
hline &&&\
sinalpha+sinbeta=2sin{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&&
sinalpha-sinbeta=2sin{dfrac{alpha-beta}2}cos{dfrac{alpha+beta}2}\&&&\
cosalpha+cosbeta=2cos{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&& cosalpha
-cosbeta=-2sin{dfrac{alpha-beta}2}sin{dfrac{alpha+beta}2}\&&&\
mathrm{tg}, alpha pm mathrm{tg},
beta=dfrac{sin{(alphapmbeta)}}{cosalphacosbeta} &&&
mathrm{ctg}, alphapm mathrm{ctg}, beta= — dfrac{sin{(alphapm beta)}}{sinalphasinbeta}\&&&\
hline
end{array}]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin{array}{|l|r|}
hline &\
sin{2alpha}=dfrac{2mathrm{tg}, alpha}{1+mathrm{tg}^2, alpha} & cos{2alpha}=dfrac{1-mathrm{tg}^2, alpha}{1+mathrm{tg}^2, alpha}\&\
cosalphane 0 & sinalphane 0\
hline
end{array}]
(blacktriangleright) Формула вспомогательного аргумента: [begin{array}{|c|}
hline text{Частный случай}\
hline \
sinalphapm cosalpha=sqrt2cdot
sin{left(alphapm dfrac{pi}4right)}\\
sqrt3sinalphapm cosalpha=2sin{left(alphapm dfrac{pi}6right)}\\
sinalphapm sqrt3cosalpha=2sin{left(xpm dfrac{pi}3right)}\\
hline text{Общий случай}\
hline\
asinalphapm bcosalpha=sqrt{a^2+b^2}cdot sin{(alphapm
phi)}, cosphi=dfrac a{sqrt{a^2+b^2}}, sinphi=dfrac
b{sqrt{a^2+b^2}}\\
hline
end{array}]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
(blacktriangleright) Вывод формулы косинуса разности углов (cos{(alpha
-beta)}=cosalphacosbeta+sinalphasinbeta)
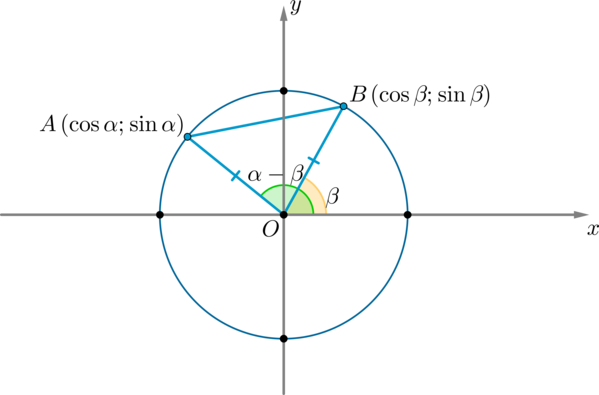
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (beta). Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(cosbeta;sinbeta)).
Рассмотрим (triangle AOB: angle AOB=alpha-beta). По теореме косинусов:
(AB^2=AO^2+BO^2-2AOcdot BOcdot
cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
(AB^2=(cosalpha-cosbeta)^2+(sinalpha-sinbeta)^2=cos^2alpha-2cosalphacosbeta+cos^2beta+)
(+sin^2alpha-2sinalphasinbeta+sin^2beta=big(cos^2alpha+sin^2alphabig)+big(cos^2beta+sin^2betabig)-2big(cosalphacosbeta+sinalphasinbetabig)=)
(=1+1-2big(cosalphacosbeta+sinalphasinbetabig) (2))
Таким образом, сравнивая равенства ((1)) и ((2)):
(1+1-2big(cosalphacosbeta+sinalphasinbetabig)=1+1-2cos(alpha-beta))
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)):
1) (cos(alpha+beta)=cos(alpha-(-beta))=cosalphacos(-beta)+sinalphasin(-beta)=cosalphacosbeta-sinalphasinbeta)
2) (sin(alpha+beta)=cos(90^circ-(alpha+beta))=cos((90^circ-alpha)-beta)=)
(+cos(90^circ-alpha)cosbeta+sin(90^circ-alpha)sinbeta=sinalphacosbeta+cosalphasinbeta)
3) (sin(alpha-beta)=sin(alpha+(-beta))=sinalphacos(-beta)+sin(-beta)cosalpha=sinalphacosbeta-sinbetacosalpha)
4) (mathrm{tg},(alphapmbeta)=dfrac{sin (alphapmbeta)}{cos
(alphapmbeta)}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbetampsinalphasinbeta}=)
разделим числитель и знаменатель дроби на (cosalphacosbetane
0)
(при (cosalpha=0 Rightarrow
mathrm{tg},(alphapmbeta)=mp mathrm{ctg},beta), при (cosbeta=0 Rightarrow
mathrm{tg},(alphapmbeta)=pm mathrm{ctg},alpha)):
(=dfrac{mathrm{tg},alphapmmathrm{tg},beta}{1mpmathrm{tg},alphacdot
mathrm{tg},beta})
Таким образом, данная формула верна только при (cosalphacosbetane 0).
5) Аналогично, только делением на (sinalphasinbetane 0), выводится формула котангенса суммы/разности двух углов.
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin
2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
2) (cos2alpha=cos(alpha+alpha)=cosalphacosalpha-sinalphasinalpha=cos^2alpha-sin^2alpha)
Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1), получим еще две формулы для косинуса двойного угла:
2.1) (cos2alpha=cos^2alpha-sin^2alpha=cos^2alpha-(1-cos^2alpha)=2cos^2alpha-1)
2.2) (cos2alpha=cos^2alpha-sin^2alpha=(1-sin^2alpha)-sin^2alpha=1-2sin^2alpha)
3) (mathrm{tg},2alpha=dfrac{sin2alpha}{cos2alpha}=dfrac{2sinalphacosalpha}{cos^2alpha-sin^2alpha}=)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm{tg},2alpha=0)):
(=mathrm{tg},2alpha=dfrac{2mathrm{tg},alpha}{1-mathrm{tg}^2,alpha})
Таким образом, эта формула верна только при (cosalphane 0), а также при (cos2alphane 0) (чтобы существовал сам (mathrm{tg},2alpha)).
4) (mathrm{ctg},2alpha=dfrac{cos^2alpha-sin^2alpha}{2sinalphacosalpha}=dfrac{mathrm{ctg}^2,alpha-1}{2mathrm{ctg},alpha})
По тем же причинам при (sinalphane 0, sin2alphane 0).
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot
2sinalphacosalpha=)
(=sinalpha-2sin^3alpha+2sinalpha(1-sin^2alpha)=3sinalpha-4sin^3alpha)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow
cos^2alpha=dfrac{1+cos2alpha}2)
2) (cos2alpha=1-2sin^2alpha Rightarrow
sin^2alpha=dfrac{1-cos2alpha}2)
Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1).
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
(cos(alpha-beta)=cosalphacosbeta+sinalphasinbeta)
(cos(alpha+beta)=cosalphacosbeta-sinalphasinbeta)
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta
Rightarrow
cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
(sinalphasinbeta=dfrac12Big(cos(alpha-beta)-cos(alpha+beta)Big))
3) Сложим формулы синуса суммы и синуса разности двух углов:
(sin(alpha+beta)=sinalphacosbeta+sinbetacosalpha)
(sin(alpha-beta)=sinalphacosbeta-sinbetacosalpha)
Получим: (sinalphacosbeta=dfrac12Big(sin(alpha-beta)+sin(alpha+beta)Big))
(blacktriangleright) Вывод формул суммы/разности функций:
Обозначим (alpha+beta=x, alpha-beta=y). Тогда: (alpha=dfrac{x+y}2, beta=dfrac{x-y}2). Подставим эти значения в предыдущие три формулы:
1) (2cos{dfrac{x+y}2}cos{dfrac{x-y}2}=cos x+cos y)
Получили формулу суммы косинусов.
2) (2sin {dfrac{x+y}2}sin {dfrac{x-y}2}=cos y-cos x)
Получили формулу разности косинусов.
3) (2sin {dfrac{x+y}2}cos {dfrac{x-y}2}=sin y+sin x)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
(sin x-sin y=sin x+sin(-y)=2sin {dfrac{x-y}2}cos
{dfrac{x+y}2})
5) (mathrm{tg},alphapmmathrm{tg},beta=dfrac{sinalpha}{cosalpha}pmdfrac{sinbeta}{cosbeta}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbeta}=dfrac{sin(alphapmbeta)}{cosalphacosbeta})
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) (sin2alpha=dfrac{sin2alpha}1=dfrac{2sinalphacosalpha}{sin^2alpha+cos^2alpha}=)
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0)):)
(=dfrac{2mathrm{tg},alpha}{1+mathrm{tg}^2,alpha})
2) Так же, только делением на (sin^2alpha), выводится формула для косинуса.
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение (asin x+bcos x). Домножим и разделим это выражение на (sqrt{a^2+b^2},):
(asin x+bcos x=sqrt{a^2+b^2}left(dfrac a{sqrt{a^2+b^2}}sin x+
dfrac b{sqrt{a^2+b^2}}cos x right)=sqrt{a^2+b^2}big(a_1sin x+b_1cos xbig))
Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1),
т.к. (left(dfrac a{sqrt{a^2+b^2}}right)^2+left(dfrac
b{sqrt{a^2+b^2}}right)^2=dfrac{a^2+b^2}{a^2+b^2}=1)
Таким образом, можно утверждать, что существует такой угол (phi), для которого, например, (cos phi=a_1, sin phi=b_1). Тогда наше выражение примет вид:
(sqrt{a^2+b^2},big(cos phi sin x+sin phicos
xbig)=sqrt{a^2+b^2},sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [{large{asin x+bcos x=sqrt{a^2+b^2},sin (x+phi),}} quad text{где } cos phi=dfrac
a{sqrt{a^2+b^2}}] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt{a^2+b^2},cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1{sqrt2}sin
xpmdfrac1{sqrt2}cos xright)=sqrt2, sin
left(xpmdfrac{pi}4right))
(b) sqrt3sin xpmcos x=2left(dfrac{sqrt3}2sin xpm
dfrac12cos xright)=2, sin left(xpmdfrac{pi}6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin
xpmdfrac{sqrt3}2cos
xright)=2,sinleft(xpmdfrac{pi}3right))
Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус — это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство — формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$




 $$
$$