Предмет: Геометрия,
автор: крут2014
Ответы
Автор ответа: UluanaV
0
Решение в прикрепленном файле.
Приложения:

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Биология,
автор: andrey1514628
Плоды томатов бывают красные и желтые.Какое потомство можно ожидать от скрещивания гетерозиготных томатов с красными плодами с особью, гомозиготной по рецессивным признакам.
4 года назад
Предмет: Физика,
автор: Аноним
будет ли отражаться красный свет от красной поверхности? от синей?
4 года назад
Предмет: Математика,
автор: steysi5
Переделать многочлен на стандартный многочлен
А) (7y2-4y+2)-(5y2-3y+7)=
Б) -4a(a3-3a2-3)=
4 года назад
Предмет: Физика,
автор: tottiaka
чем можно объяснить увеличение длины проволоки при нагревании
7 лет назад
Предмет: Биология,
автор: 5367356
рассмотри молодые корни луковицы Определить тип корневой системы Подпиши на схеме Из каких корней состоит
7 лет назад
Задание 579
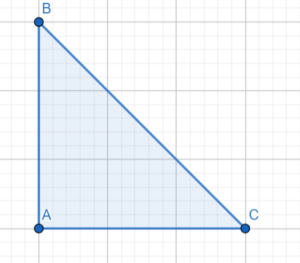
Постройте угол: 1) тангенс которого равен 4/5 ; 2) синус которого равен 2/3.
Ответ:
1) tg (∠ABD) = AC/CB = 4/5
2) sin (∠ABD) = AC/AB – 2/3
Задание 580
Постройте угол: 1) косинус которого равен 1/4 ; 2) котангенс которого равен ½
Ответ:
1) cos (∠CAB) = AC/AB = 1/4
2) cts (∠CAB) = AC/CB = ½
Задание 581
Катет и гипотенуза прямоугольного треугольника соответственно равны 8 см и 10 см. Найдите: 1) синус угла, противолежащего меньшему катету; 2) косинус угла, прилежащего к большему катету; 3) тангенс угла, противолежащего меньшему катету; 4) котангенс угла, прилежащего к большему катету.
Ответ:
AC² = BC²-AB²
AC² = 10² — 8² = 100-64= 36
АС = √ 36 AC = 6
1) sin = AC/BC sin = 6/10 = 0.6
2) cos = AB/BC cos = 8/10 = 0.8
3) tg = AC/AB tg = 6/8 = 0.75
4) ctg = AB/AC ctg = 8/6 ≈ 1.3
Задание 582
Катеты прямоугольного треугольника равны 3 см и 2 см. Найдите: 1) тангенс угла, прилежащего к большему катету; 2) синус угла, противолежащего меньшему катету; 3) косинус угла, прилежащего к большему катету; 4) котангенс угла, противолежащего большему катету.
Ответ:
Синус — это отношение противолежащего катета к гипотенузе.
Косинус — это отношение прилежащего катета к гипотенузе.
Тангенс — это отношение противолежащего катета к прилежащему.
Котангенс — это отношение прилежащего катета к противолежащему.
По условию катеты прямоугольного треугольника равны 3 см и 2 см, тогда по теореме Пифагора найдем его гипотенузу: 3² + 2² = 9 + 4 = 13, т.е. гипотенуза равна √13 см (см. рис. к задаче).
1) больший катет равен 3 см, поэтому тангенс этого угла будет равен 2/3;
2) меньший катет равен 2 см, поэтому синус нужного угла буде равен 2/√13;
3) больший катет равен 3 см, поэтому косинус нужного угла будет равен 3/√13;
4)больший катет равен 3 см, поэтому котангенс нужного угла будет равен 2/3.
Задание 583
Найдите значение выражения: 1) cos2 45° + tg2 60°; 2) 2cos2 60° — sin2 30° + sin 60° ctg 60°.
Ответ:
а) 2 sin 60°•ctg 60° = 2 * √3/2 * √3/3 = (3*2)/(3*2) = 1
в) 7 tg30°•ctg 30° = 7 * √3/3 * √3 = 7
б) 2 sin 45° — 4 cos 30° = 2 * √2/2 — 4 * √3/2=√2- 2√3
г) 6 ctg 60°- 2 sin 60° = 6 * √3/3 — 2 * √3/2 = 2√3 — √3 = √3
Задание 584
Найдите значение выражения: 1) cos2 30° — sin2 45°; 2) 3tg2 30° + 4tg 45° + cos 30° ctg 30°.
Ответ:
1) (√2/2)² + (√3)² = √2²/2² + 3 = 2/4 + 3 = 0,5 + 3 = 3,5
2) 2 * (½)² – (½)² + √3/2 * √3/3 = ̶2̶¹ * 1/ ̶4̶² – ¼ + ̶3̶¹/2* ̶3̶¹ = ½ – ¼ + ½ = 1 – ¼ = 1 – 0,25 = 0,75
Задание 585
В треугольнике ABC известно, что /С = 90°, ВС = 77 см, АВ = 125 см. Найдите синусы острых углов треугольника.
Ответ:
Дано:
ΔABC (∠C = 90°)
BC = 77
AB = 125
Найти:
sin ∠A; sin ∠B
Решение:
По теореме Пифагора:
AB² = AC² + BC²;
AC² = 125² — 77² = (125 — 77)(125 + 77) = 48 · 202
AC = 4√606 ≈ 98,5
sin A = BC ÷ AB = 77 ÷ 125 = 0,616
sin B = AC ÷ AB ≈ 98,5 ÷ 125 = 0,788
Задание 586
В треугольнике ABC известно, что ∠C = 90°, ВС = 41 см, АС = 20 см. Найдите косинусы острых углов треугольника.
Ответ:
косинус угла А равен= АС/АВ
косинус угла В = ВС/АВ
АВ- гипотинуза , по теореме Пифагора
находим
АВ в квадрате = 20 в квадрате + 41 в квадрате = приблизительно 45,6
косинус А = 20/45,6= приблизительно 0,44
косинус В = 41/45,6= приблизительно 0,89
Задание 587
Найдите sin a, tg α и ctg α, если cos α = 1/3
Ответ:
Задание 588
Найдите cos β, tg β и ctg β, если sin β = 4/5.
Ответ:
По основной тригонометрической формуле:
сosB=√(1-sin^2B)=√(1-16/25)=3/5.
tgB=sinB/coB=3/5 : 4/5=3/4.
ctgB=1/tgB=1 : 3/4 =4/3.
Задание 589
Синус острого угла прямоугольного треугольника равен √3/3. Найдите синус, косинус, тангенс и котангенс второго острого угла этого треугольника.
Ответ:
Дано треугольник АВС угол С = 90 sin = √3/3
Найти углы sin в cos в tg в ctg в
Решение
составим уравнение
а = 90-в
в = 90-а
на основание чего получим
sin в = sin(90-a)
sin (90-a) = cos a = √1-sin^2a = √1-(√3/3)^2 = √6/3
проведем расчет углов:
cos в = √1-sin^2в = √1-(√6/3)^2 = √3/3
tg в = sin в / cos в = √6*3/3*√3 = √2
ctg в = 1/ tgв = 1/√2 = √2/2
Ответ: √6/3 , √3/3, √2, √2/2
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
2 . В треугольнике угол равен , , . Найдите .
Найдем по теореме Пифагора.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Синус угла в обычном треугольнике
Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.
Синус угла в прямоугольном треугольнике
Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:
- α – острый угол, синус которого нужно найти;
- с – гипотенуза;
- b – прилежащий катет;
- a – противолежащий катет.
Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.
Синус угла в произвольном треугольнике
Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.
a² = b² + c² – 2*b*c*cos(α)
Из данной формулы можно найти косинус: cos(α) = (b² + c² – a²)/(2*b*c)
А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:
Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.
Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
http://dudom.ru/kompjutery/sinus-ugla-v-obychnom-treugolnike/
http://zaochnik.com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/
Содержание:
- Синус угла в треугольнике
- Синус произвольного угла
Синус угла в треугольнике
Определение
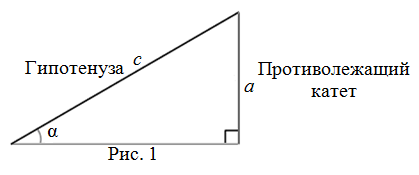
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу
катета к гипотенузе (рис. 1):
$$sin alpha=frac{a}{c}$$
Пример
Задание. Пусть задан прямоугольный треугольник, у которого гипотенуза равна 5 см,
а один из катетов 3 см. Найти синус противолежащего этому катету угла.
Решение. Согласно определению имеем, что искомое значение равно отношению
противолежащего катета к гипотенузе, то есть
$$sin alpha=frac{3}{5}$$
Ответ. $sin alpha=frac{3}{5}$
Синус произвольного угла
Определение
Синусом произвольного угла
$alpha$, образованного осью
$Ox$ и произвольным радиус вектором
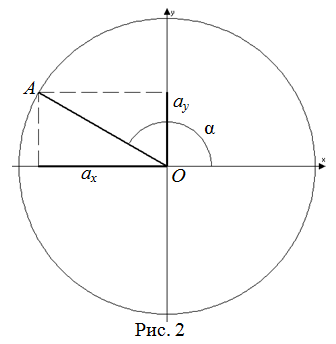
$overline{O A}=left(a_{x} ; a_{y}right)$ (рисунок 2), называется отношение
проекции этого вектора на ось $Oy$ к его длине
$a=|overline{O A}|$:
$sin alpha=frac{a_{y}}{a}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти синус угла, образованного вектором
$bar{a}=(-1 ; 2)$ с осью абсцисс.
Решение. Согласно определению синуса угла получаем:
$sin alpha=frac{2}{sqrt{(-1)^{2}+2^{2}}}=frac{2}{sqrt{5}}=frac{2 sqrt{5}}{5}$
Ответ. $sin alpha=frac{2 sqrt{5}}{5}$
Читать дальше: что такое косинус угла.
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
3
Катеты прямоугольного треугольника равны 3 см и 2 см
Найти
1)тангенс угла,прилежащего к большему катету
2)синус угла,противолежащего меньшему катету
ПОМОГИТЕ ПОЖАЛУЙСТА
1 ответ:
0
0
Тангенс — это отношение противолежащего катета к прилежащему.
Найдём гипотенузу по теореме Пифагора
Синус — это отношение противолежащего катета к гипотенузе
Читайте также
Если точки BDM расположены на прямой именно в этой последовательности, то расстояние BM можно вычислить сложив два отрезка ВD и MD получим 7+16=23(см)
ответ: расстоянием между ВМ 23см
1.дано:треугольник RSО,треугольникPOT
RO=OT
PO=OS
УГОЛ ROS = УГЛУ TOP
РЕШЕНИЕ:
RO=OT
PO=OS
УГОЛ ROS = УГЛУ TOP, ТО RSO=треугольникуPOT ПО ДВУМ СТОРОНАМ И УГЛУ МЕЖДУ НИМИ
<span> Угловой коэффициент прямой, проходящей через точки с координатами (-2:0) и (0:2), равен:
к =( у</span>₂-у₁) / (х₂ — х₁)
к = (2-0) / (0-(-2)) = 2 / 4 = 0,5
Чертежа нет
ЕСЛИ СЕКУЩАЯ ПЕРЕСЕКАЕТ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, то накрест лежащие углы равны
150:2=75 градусов
Ответ углы=75° и 105°
ΔАВC прямоугольный. <B=90°
OB- радиус.
<ABO=x, <ACB=8x
ΔCOB равнобедренный: ОВ=ОВ=R. =>
<OCB= <OBC=8x
<B=<ABO+<OBC
90°=x+8x
x=10, <u><ABO=10°</u>
<u><ACB=80°</u>