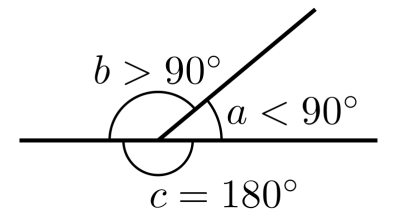Как найти синус смежного угла зная синус - AvtoShod.ru

Во-первых, что такое смежный угол? Это угол, который в сумме с заданным углом даёт 180 градусов. Приведём чертёж для пояснения вычислений.

Пусть дан угол ?0, смежный с углом α0 будет угол α1, причём α0 + α1 = 180°.

Если известен синус угла ?0, то по формулам приведения находим синус смежного угла ?1.

sin (а1) = sin (а0)= sin (180° — а1).

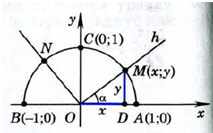
Если начертить угол а0 в системе координат, и синус углов а0 и а1 представляет в системе координат одну и ту же ординату у, равную синусу угла.

Здесь угол а0 = углу а, а угол а1 = (180° — а).

И sin (а) = MD = у = sin (180° — а).

Здесь ОМ — единичный вектор, у — ордината точки М и также синус угла ?.

Источник

Как найти синус смежного угла?

Как соотносятся синусы смежных углов?

3 ответа:

1

0

Ответ: sin A = sin B вот так вроде ну лучше посмотри в интернете

1

0

Смежные углы это 2 угла, сумма которых равна 180°. Смотри рисунок.

Смежные углы имеют общую вершину и одну общую сторону. Итак, сумма углов а + b = 180°. Отсюда а = 180° — b. Далее берем синусы: sina = sin(180° — b) = sinb. Итак имеем

sina = sinb.

1

0

Пусть дан угол ?0, смежный с углом α0 будет угол α1, причём α0 + α1 = 180°.

Если известен синус угла ?0, то по формулам приведения находим синус смежного угла ?1.

sin (а1) = sin (а0)= sin (180° — а1).

Здесь угол а0 = углу а, а угол а1 = (180° — а).

И sin (а) = MD = у = sin (180° — а).

Здесь ОМ — единичный вектор, у — ордината точки М и также синус угла ?.

Читайте также

Тут можно посоветовать одну вещь. Уяснить как соотносятся разные тригонометрические функции. Например, sin(60) = sqrt(3)/2 (sqrt — квадратный корень), тогда, зная соотношение sin(a)^2 + cos(a)^2 = 1, можно легко найти, что cos(60) = sqrt(1 — (sqrt(3)/2)^2) = sqrt(1/4) = 1/2. Также tg(60) = sin(60)/cos(60) = sqrt(3)/2 / (1/2) = sqrt(3), а ctg(60) = 1/tg(60) = 1/sqrt(3). То есть зная несколько тригонометрических формул, можно из одного заученного значения угла вывести несколько других. Достаточно знать значения в 0, 30, 45, 60 и 90 градусах для одной из тригонометрических функций. Остальные могут быть легко «восстановлены». Если использовать формулы понижения степени, свойство периодичности, а также выражения для тригонометрических функций суммы и разности углов, то можно будет восстановить таблицу по трём значениям синуса sin(0) = 0, sin(90) = 1 и sin(30) = 1/2. По мере использования, таблица запомнится сама собой.

Легко запомнить, представив тригонометрический круг, разделенный на 4 четверти по 90 градусов, он заменяет все таблицы. Нарисуйте единичную окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Косинус — это будет ось абсцисс, синус — ось ординат и т.д.

Значение тангенса угла легко найти — поделив синус на косинус.

Так, как AB=BC, значит треугольник ABC-равнобедренный<wbr />, а это значит, что углы ACB и CAB равны, а значит и их синусы тоже будут равны.

<CAB=<CAH;(один и тот же угол)

А синус угла CAH, найти не составит труда:

Sin(CAH)=HC/AC=7/1<wbr />4=1/2=0,5;

<h2>Ответ:</h2>

0,5;

Если известны только углы, то

C=180-arcsin(sin A)-arcsin(sin B)

Если известна хоть одна сторона, то есть теорема синусов.

a/sin A = b/sin B = c/sin C = 2R

Зная одну сторону и два синуса, можно найти и третий синус, и остальные две стороны.

И заодно радиус описанной окружности, но это уже другая задача.

Значения синусов и косинусов (и вообще любых функций), а также некоторых чисел, например числа Пи, вычисляются разложением их в ряды. Разложение функций в ряды изучает высшая математика. Пример разложения (и вычисления) синуса приведён в ответе.

Переписывать свой ответ прямо сюда не могу, так как мне припишут неоригинальность (грубо говоря, плагиат), и удалят мой ответ, так со мной уже бывало не раз. Поэтому приходится просто дать ссылку.

Источник

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна $180^{circ}$ .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом alpha . Если угол alpha острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

$sin left( 180^{circ} - alpha right) = sin alpha;$
$cos left( 180^{circ} - alpha right) = - cos alpha;$
$tg , left( 180^{circ} - alpha right) = - , tg , alpha.$

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике ABC угол равен $90^{circ}$ , $cos A = genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}$ . Найдите тангенс внешнего угла при вершине .

Пусть varphi — внешний угол при вершине .

$cos varphi = - cos A = - genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}.$

Зная , найдем по формуле:

$genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos^2 varphi}= 1 + tg^2 , varphi.$

Получим: $tg , varphi= - genfrac{}{}{}{0}{displaystyle 1}{displaystyle 4} = - 0,25.$

2. В треугольнике ABC угол равен $90^{circ}$ , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна $90^{circ}$ , . Тогда и синус внешнего угла при вершине также равен 0,1 .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Смежные углы. Свойства смежных углов

Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.

На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:

Свойства смежных углов

1. Сумма смежных углов равна 180°

2. Если оба смежных угла равны между собой, то они являются прямыми.

3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.

4. Синусы смежных углов равны.

5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.

Справедливость пунктов 2 и 3 очевидны и следуют из (1).

Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)

То есть синусы смежных углов равны.

Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но

То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Источник

Геометрия, опубликовано 2018-08-22 14:25:10 by Гость

Найдите синус угла,если синус смежного с ним угла равен 0,3

Ответ оставил Гость

Пусть угол равен α, тогда смежный с ним 180-α
sin(180-α)=sinα=0.3

Не нашли ответа?

Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Геометрия.

Источник

Как найти синус смежного угла?

Внешний угол треугольника. Синус и косинус внешнего угла

Смежные углы. Свойства смежных углов

Свойства смежных углов

Найдите синус угла,если синус смежного с ним угла равен 0,3

Не пропустите также: