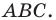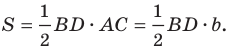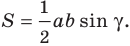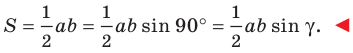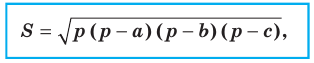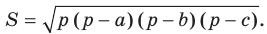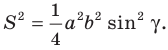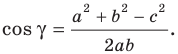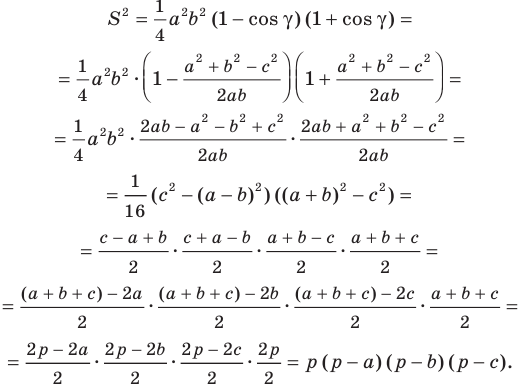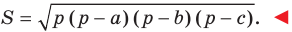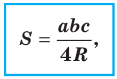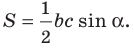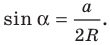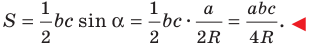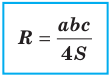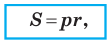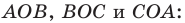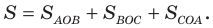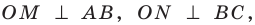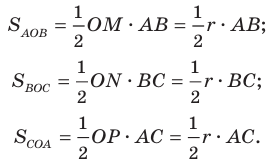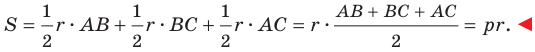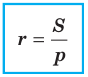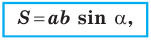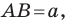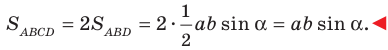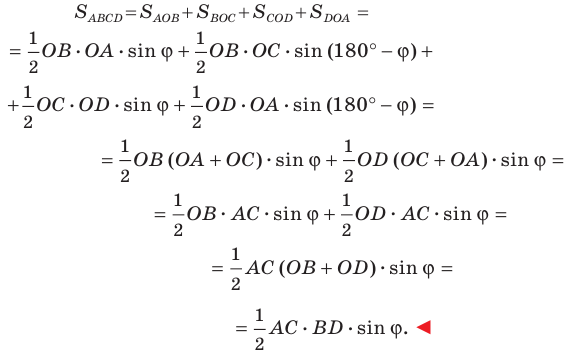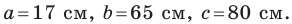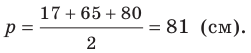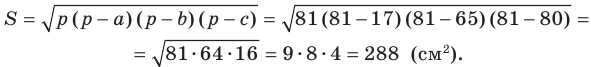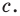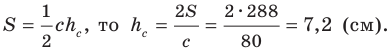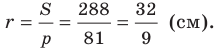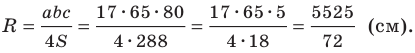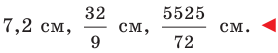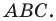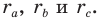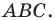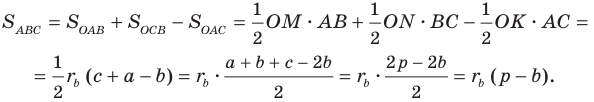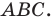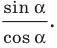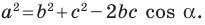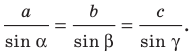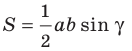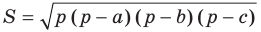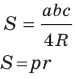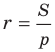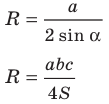Как найти синус угла по сторонам треугольника
Синус — это одна из базовых тригонометрических функций. Первоначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для более сложных случаев с произвольными треугольниками.
Инструкция
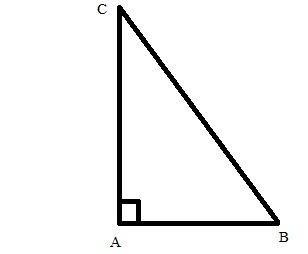
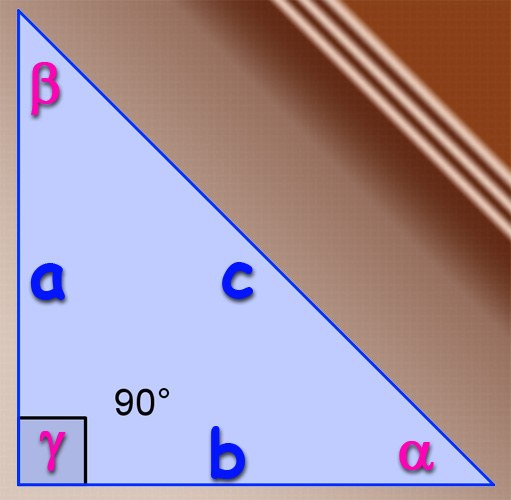
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В — по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С). А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С)²).
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой — длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)). А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы двух других углов можно найти по аналогичным формулам.
Видео по теме
Источники:
- треугольник синус
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Я так понял, что задача сводится к тому, что нам неизвестен угол треугольника, и нам нужно его найти.
Для того чтобы найти синус угла, а затем и сам угол в произвольном треугольнике, необходимо знать длины двух сторон: стороны, противолежащей искомому углу, и какой-либо другой стороны — и ещё величину угла, противолежащего этой последней стороне.
А затем нужно применить теорему синусов.
Обозначим искомый (неизвестный) угол как A, противолежащую сторону — a, другую известную сторону — b, известный противолежащий этой стороне угол — B.
По теореме синусов: a/sin(A) = b/sin(B).
Отсюда: sin(A) = a * sin(B)/b;
A = arcsin[a * sin(B)/b].
Как искать синус угла
Содержание
- Игры с линейкой и карандашом
- Найти синус для угла больше 90°
- Вычисление синуса по другим тригонометрическим функциям
- Как находить синус по трём сторонам треугольника
- Линии тригонометрических функций
- Значения основных функций тригонометрии
- Сведение к углу
- Использование формул
- Частные случаи
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
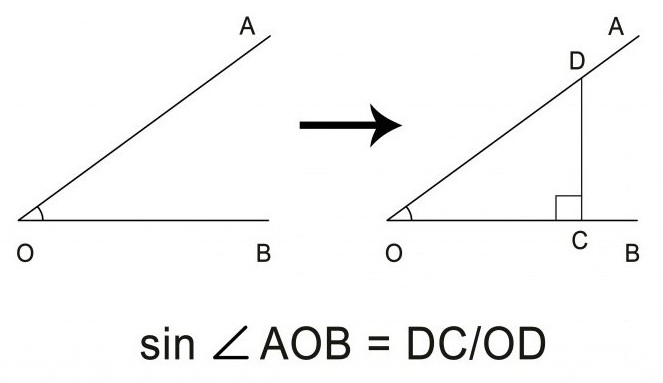
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
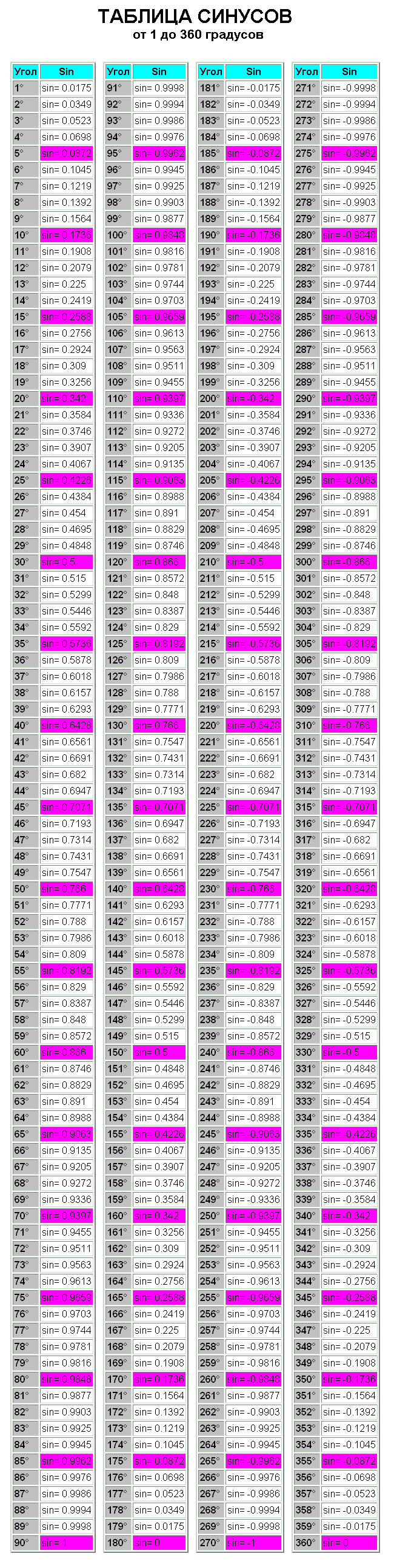
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
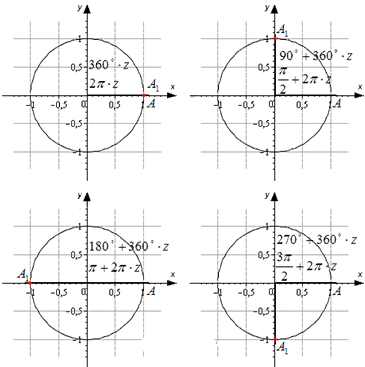
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
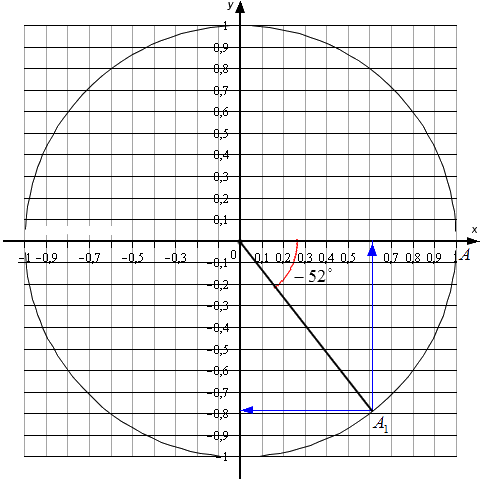
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
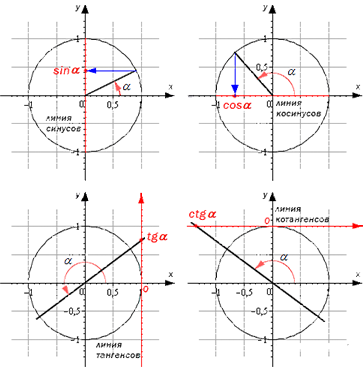
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
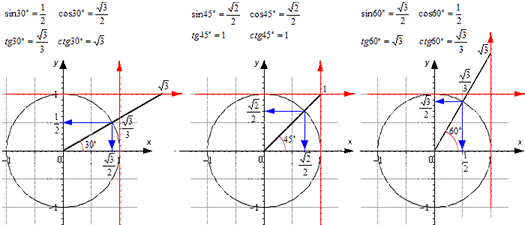
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
2 . В треугольнике угол равен , , . Найдите .
Найдем по теореме Пифагора.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Содержание:
В этой лекции вы узнаете, что представляют собой синус, косинус и тангенс угла
Решение треугольников
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам).
Синус, косинус и тангенс угла от 0 до 180
Понятия синуса, косинуса и тангенса острого угла вам известны из курса геометрии 8 класса. Расширим эти понятия для произвольного угла 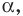
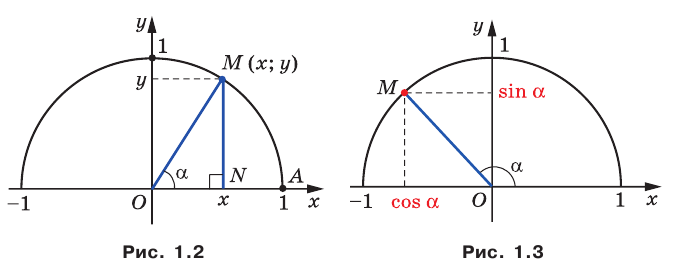
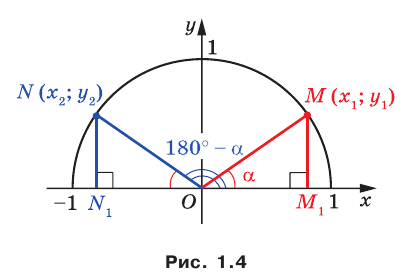
В верхней полуплоскости координатной плоскости рассмотрим полуокружность с центром в начале координат, радиус которой равен 1 (рис. 1.1). Такую полуокружность называют единичной.
Будем говорить, что углу 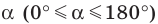
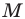
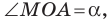
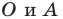
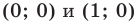

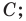
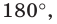
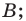
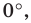
Пусть 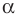
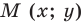
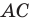
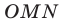
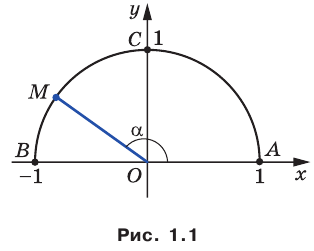
Поскольку 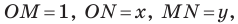
Итак, косинус и синус острого угла 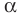
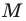
Полученный результат подсказывает, как определить синус и косинус произвольного угла 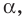
Определение. Косинусом и синусом угла 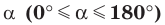
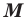
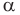
Пользуясь этим определением, можно, например, установить, что
Если 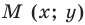
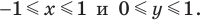
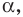
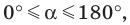
Если 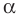
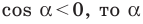
Из курса геометрии 8 класса вы знаете, что для любого острого угла а выполняются равенства:
Эти формулы остаются справедливыми также для 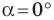
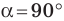
Пусть углам 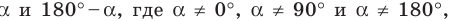
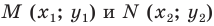
Прямоугольные треугольники 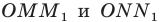
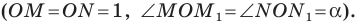
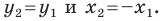
Убедитесь самостоятельно, что эти равенства остаются верными для
Если 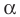
Это равенство остается верным для 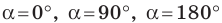
Пусть 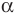
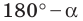
Следовательно, равенство 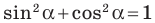
Определение. Тангенсом угла 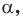
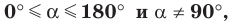
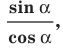
Поскольку 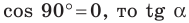
Очевидно, что каждому углу 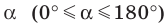
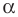
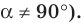
Функции 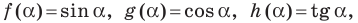
Пример №1
Докажите, что
Решение:
Пример №2
Найдите
Решение:
Имеем:
Теорема косинусов
Из первого признака равенства треугольников следует, что две стороны и угол между ними однозначно определяют треугольник. А значит, по указанным элементам можно, например, найти третью сторону треугольника. Как это сделать, показывает следующая теорема.
Теорема 2.1 (теорема косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
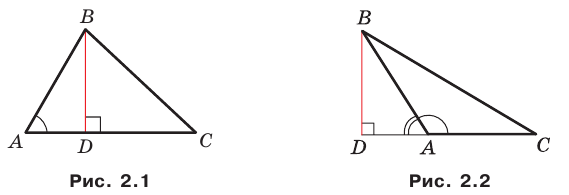
Доказательство: Рассмотрим треугольник 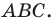
Возможны три случая:
- угол
острый;
- угол
тупой;
- угол
прямой.
Первый случай. Пусть угол 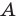
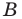
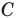
Пусть 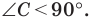
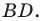
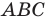
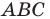
В прямоугольном треугольнике
Пусть 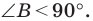
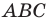

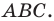
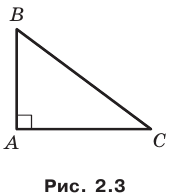
Второй случай. Пусть угол 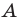
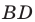
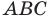
В прямоугольном треугольнике
В прямоугольном треугольнике BDC:
Третий случай. Пусть угол 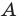
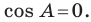
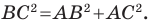
Доказательство теоремы косинусов показывает, что теорема Пифагора является частным случаем теоремы косинусов, а теорема косинусов является обобщением теоремы Пифагора.
Если воспользоваться обозначениями для длин сторон и величин углов треугольника 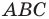
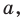
С помощью теоремы косинусов, зная три стороны треугольника, можно определить, является ли он остроугольным, тупоугольным или прямоугольным.
Теорема 2.2 (следствие из теоремы косинусов). Пусть 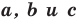
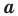
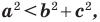
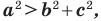
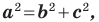
Доказательство: По теореме косинусов
Отсюда
Пусть 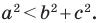
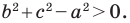

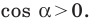
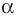
Поскольку 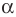
Пусть 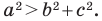
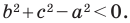

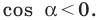
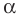
Пусть 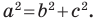

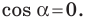
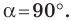
Пример №3
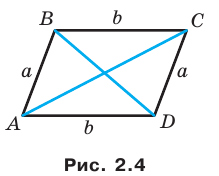
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Решение:
На рисунке 2.4 изображен параллелограмм 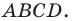
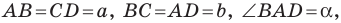
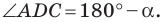
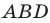
Из треугольника 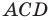
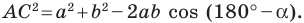
Сложив равенства (1) и (2), получим:
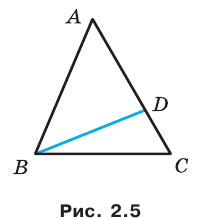
Пример №4
В треугольнике 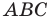
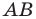
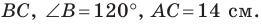
Решение:
По теореме косинусов
Пусть 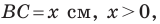
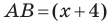
Имеем:
Корень -10 не удовлетворяет условию
Следовательно,
Ответ:
Пример №5
На стороне 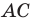
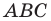
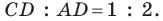
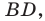
Решение:
По теореме косинусов из треугольника 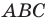
Отсюда
Поскольку 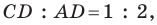
Тогда из треугольника 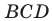
Следовательно,
Ответ:
Пример №6
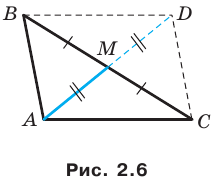
Две стороны треугольника равны 23 см и 30 см, а медиана, проведенная к большей из известных сторон, — 10 см. Найдите третью сторону треугольника.
Решение:
Пусть в треугольнике 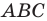
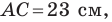
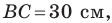
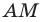
На продолжении отрезка 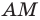
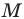
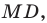
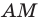
В четырехугольнике 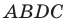
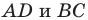
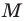
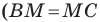
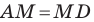
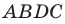
Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (см. ключевую задачу 1), то
Тогда
Ответ: 11 см.
Теорема синусов
При доказательстве ряда теорем и решении многих задач применяют следующую лемму.
Лемма. Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Доказательство: На рисунке 3.1 отрезок 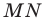
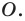
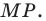
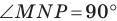
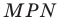
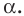
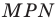
Все вписанные углы, опирающиеся на хорду 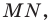
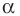
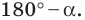
Из второго признака равенства треугольников следует, что сторона
и два прилежащих к ней угла однозначно определяют треугольник. Следовательно, по указанным элементам можно найти две другие стороны треугольника. Как это сделать, подсказывает следующая теорема.
Теорема 3.1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство: Пусть в треугольнике 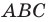
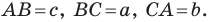
Пусть радиус описанной окружности треугольника 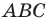
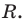
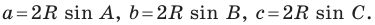
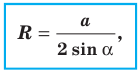
Следствие. Радиус окружности, описанной около треугольника, можно вычислить по формуле
где 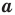
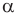
Пример №7
В треугольнике 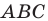
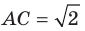
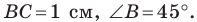
Решение:
По теореме синусов
Тогда
Поскольку 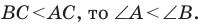
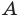
Отсюда, учитывая, что 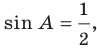
Ответ:
Пример №8
В треугольнике 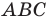
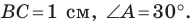
Решение:
По теореме синусов 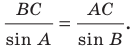
Поскольку 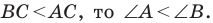
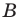
Ответ:
Пример №9
На стороне 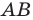
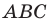
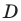
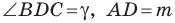
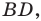
Решение:
Угол 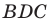
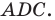
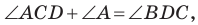
Из треугольника 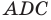
Следовательно,
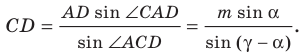
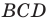
Следовательно,
Ответ:
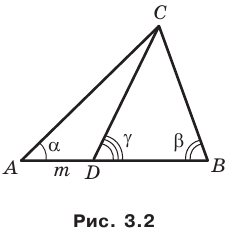
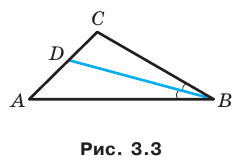
Пример №10
Отрезок 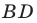
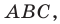
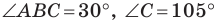
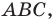
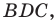
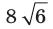
Решение:
Пусть 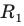
Поскольку отрезок 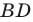
Из треугольника 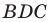
По следствию из теоремы синусов 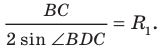
Из треугольника 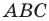
Пусть 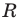
Тогда 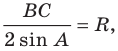
Ответ:
Как решать треугольников
Решить треугольник — это значит найти неизвестные его стороны и углы по известным сторонам и углам
Теоремы косинусов и синусов позволяют решить любой треугольник.
В следующих задачах значения тригонометрических функций будем находить с помощью калькулятора и округлять эти значения до сотых. Величины углов будем находить с помощью калькулятора и округлять эти значения до единиц. Вычисляя длины сторон, результат будем округлять до десятых.
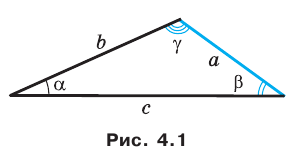
Пример №11
Решите треугольник (рис. 4.1) по стороне 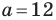
Решение:
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Имеем:
Вновь применяя теорему синусов, запишем:
Отсюда
Имеем:
Ответ:
Пример №12
Решите треугольник по двум сторонам 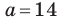
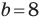
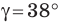
Решение:
По теореме косинусов
Отсюда
Далее имеем:
Отсюда
Используя теорему о сумме углов треугольника, получаем:
Ответ:
Пример №13
Решите треугольник по трем сторонам 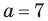
Решение:
По теореме косинусов 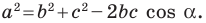
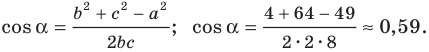
Пo теореме синусов 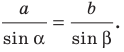
Поскольку 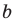
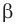
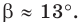
Ответ:
Пример №14
Решите треугольник по двум сторонам и углу, противолежащему одной из сторон:
Решение:
1) По теореме синусов
Отсюда
Поскольку угол 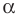
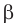
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Ответ:
2) По теореме синусов
Отсюда 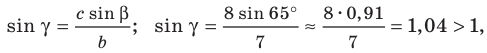
Ответ: задача не имеет решения.
3) По теореме синусов 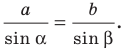
Возможны два случая: 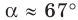
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Пo теореме синусов
Отсюда 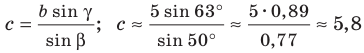
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Поскольку 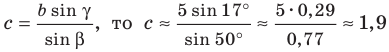
Ответ:
Тригонометрия наука об измерении треугольников
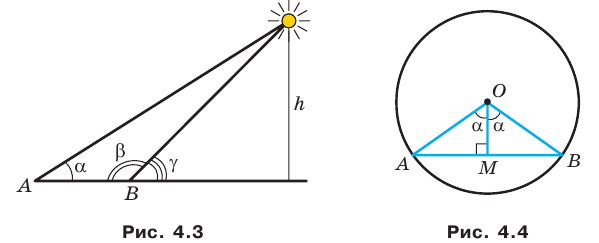
Вы знаете, что древние путешественники ориентировались по звездам и планетам. Они могли достаточно точно определить положение корабля в океане или каравана в пустыне по расположению светил на небосклоне. При этом одним из ориентиров служила высота, на которую поднималось над горизонтом то или иное небесное светило в данной местности в данный момент времени.
Понятно, что непосредственно измерить эту высоту невозможно. Поэтому ученые стали разрабатывать методы косвенных измерений. Здесь существенную роль играло решение треугольника, две вершины которого лежали на поверхности Земли, а третья являлась звездой (рис. 4.3) — знакомая вам задача 3.17.
Для решения подобных задач древним астрономам необходимо было научиться находить взаимосвязи между элементами треугольника. Так возникла тригонометрия — наука, изучающая зависимость между сторонами и углами треугольника. Термин «тригонометрия» (от греческих слов «тригонон» — треугольник и «метрео» — измерять) означает «измерение треугольников».
На рисунке 4.4 изображен центральный угол 
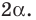
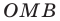
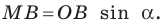
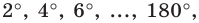
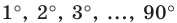
Измеряя длины полухорд, древнегреческий астроном Гиппарх (II в. до н. э.) составил первые тригонометрические таблицы.
Понятия синуса и косинуса появляются в тригонометрических трактатах индийских ученых в IV-V вв. н. э. В X в. арабские ученые оперировали понятием тангенса, которое возникло из потребностей гномоники — учения о солнечных часах (рис. 4.5).
В Европе первой работой, в которой тригонометрия рассматривалась как отдельная наука, был трактат «Пять книг о треугольниках всех видов», впервые напечатанный в 1533 г. Его автором был немецкий ученый Региомонтан (1436-1476). Этот же ученый открыл и теорему тангенсов:
где 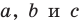
Современный вид тригонометрия приобрела в работах великого математика Леонарда Эйлера.
Леонард Эйлер
(1707-1783) Выдающийся математик, физик, механик и астроном, автор более 860 научных работ. Член Петербургской, Берлинской, Парижской академий наук, Лондонского королевского общества, многих других академий и научных обществ. Имя Эйлера встречается почти во всех областях математики: теоремы Эйлера, тождества Эйлера, углы, функции, интегралы, формулы, уравнения, подстановки и т. д.
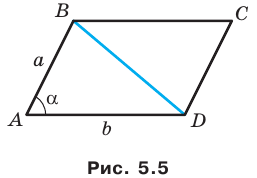
Формулы для нахождения площади треугольника
Из курса геометрии 8 класса вы знаете, что площадь 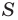
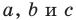
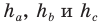
Теперь у нас появилась возможность получить еще несколько формул для нахождения площади треугольника.
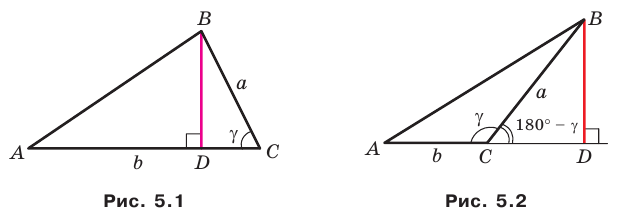
Теорема 5.1. Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
Доказательство: Рассмотрим треугольник 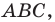
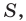
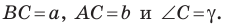
Возможны три случая:
- угол
острый (рис. 5.1);
- угол
тупой (рис. 5.2);
- угол
прямой.
На рисунках 5.1 и 5.2 проведем высоту 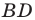
Тогда
Из прямоугольного треугольника 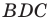
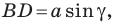
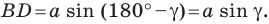
Если угол 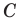
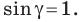
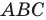
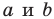
Теорема 5.2 (формула Герона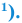
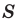
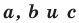
где 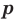
Доказательство: Рассмотрим треугольник 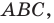
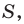
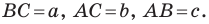
Пусть 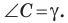
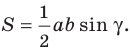
По теореме косинусов 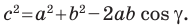
Поскольку 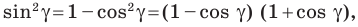
Отсюда
Теорема 5.3. Площадь 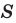
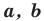
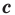
где 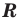
Доказательство: Рассмотрим треугольник 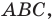
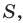
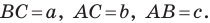
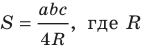
Пусть 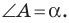
Из леммы п. 3 следует, что
Тогда
Заметим, что доказанная теорема позволяет находить радиус описанной окружности треугольника по формуле
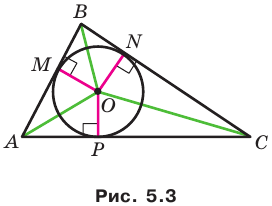
Теорема 5.4. Площадь треугольника равна произведению его полупериметра и радиуса вписанной окружности.
Доказательство: На рисунке 5.3 изображен треугольник 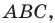
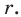
где 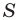
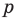
Пусть точка 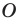
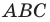
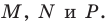
Проведем радиусы в точки касания. Получаем: 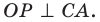
Следовательно,
Теорему 5.4 обобщает следующая теорема.
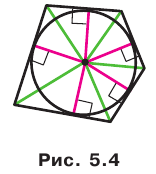
Теорема 5.5. Площадь описанного многоугольника равна произведению его полупериметра и радиуса вписанной окружности.
Докажите эту теорему самостоятельно (рис. 5.4).
Заметим, что теорема 5.5 позволяет находить радиус вписанной окружности многоугольника по формуле
Пример №15
Докажите, что площадь 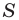
где 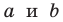
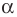
Решение:
Рассмотрим параллелограмм 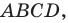
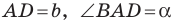
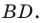
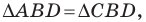
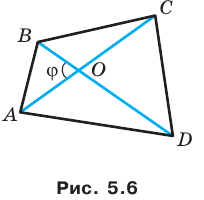
Пример №16
Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей и синуса угла между ними.
Решение:
Пусть угол между диагоналями 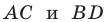
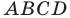
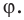
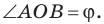
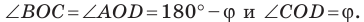
Пример №17
Стороны треугольника равны 17 см, 65 см и 80 см. Найдите наименьшую высоту треугольника, радиусы его вписанной и описанной окружностей.
Решение:
Пусть
Найдем полупериметр треугольника:
Площадь треугольника вычислим по формуле Герона:
Наименьшей высотой треугольника является высота, проведенная к его наибольшей стороне, длина которой равна
Поскольку
Радиус вписанной окружности
Радиус описанной окружности
Ответ:
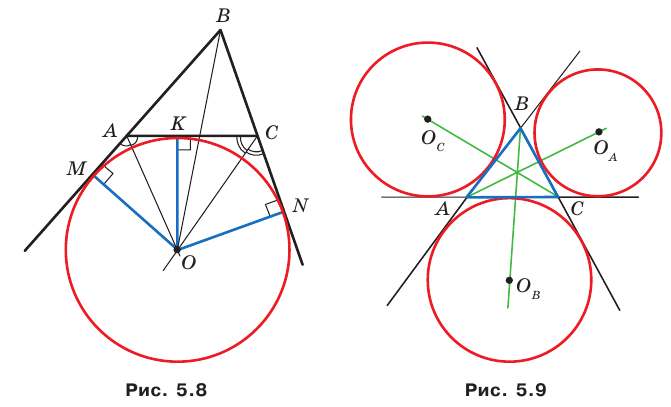
Вневписанная окружность треугольника
Проведем биссектрисы двух внешних углов с вершинами 
Проведем три перпендикуляра: 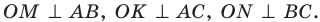
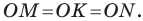
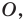
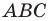
Поскольку 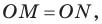
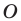
Любой треугольник имеет три вневписанные окружности. На рисунке 5.9 их центры обозначены 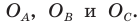
По свойству касательных, проведенных к окружности через одну точку, имеем: 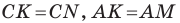
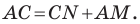
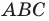
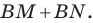
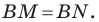
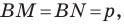
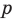
Имеем:
Отсюда 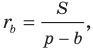
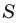
Аналогично можно показать, что
Справочный материал
Косинус и синус
Косинусом и синусом угла 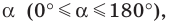
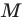
Тангенс
Тангенсом угла 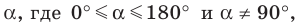
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними:
Следствие из теоремы косинусов
Пусть 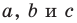
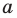
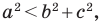
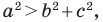
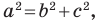
Лемма о хорде окружности
Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
Формулы для нахождения площади треугольника
Формула Герона:
Формула для нахождения радиуса окружности, вписанной в треугольник
Формулы для нахождения радиуса окружности, описанной около треугольника
Площадь многоугольника, описанного около окружности
Площадь многоугольника, описанного около окружности, равна произведению его полупериметра и радиуса вписанной окружности.
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Треугольник
Совет 1: Как обнаружить синус угла по сторонам треугольника
Синус – это одна из базовых тригонометрических функций. Изначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для больше трудных случаев с произвольными треугольниками.
Инструкция
1. Если рассматриваемый треугольник является прямоугольным, то дозволено применять базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего наоборот этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла ?, лежащего наоборот катета А, определяйте по формуле ?=А/С, а синус угла ?, лежащего наоборот катета В – по формуле ?=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, потому что угол, лежащий наоборот гипотенузы неизменно равен 90°, а его синус неизменно равен единице.
2. Для нахождения синусов углов в произвольном треугольнике, как это ни необычно, проще применять не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина всякий стороны равна сумме квадратов длин 2-х других сторон без удвоенного произведения этих длин на косинус угла между ними: А?=В?+С2-2*В*С*cos(?). Из этой теоремы дозволено вывести формулу для нахождения косинуса: cos(?)=(В?+С?-А?)/(2*В*С). А от того что сумма квадратов синуса и косинуса одного и того же угла неизменно равна единице, то дозволено вывести и формулу для нахождения синуса угла ?: sin(?)=?(1-(cos(?))?)= ?(1-(В?+С?-А?)?/(2*В*С)?).
3. Воспользуйтесь для нахождения синуса угла двумя различными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в иной – длины 2-х сторон и синус угла между ними. Потому что итоги их будут равны, то из тождества дозволено выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=?*?((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)). А вторую формулу дозволено написать так: S=А*В*sin(?). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего наоборот стороны С: sin(?)= ?*?((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы 2-х других углов дозволено обнаружить по аналогичным формулам.
Совет 2: Как обнаружить синус треугольника
Прямоугольным треугольником считается треугольник, у которого один из углов прямой. Для подсчета синуса его острых углов, а также прямого угла, довольно владеть данными о его сторонах.
Вам понадобится
- Размеры сторон прямоугольного треугольника.
Инструкция
1. Отношение противолежащего катета к гипотенузе прямоугольного треугольника именуется синусом острого угла прямоугольного треугольника :Sin A = ABBCSin B = ACCBСинус 90 градусов равен 1.
2. Для того, дабы подсчитать синус того либо другого угла, дозволено воспользоваться таблицей синусов. Она представляет собой сводную таблицу из значений углов от 0 до 360 градусов и соответствующие им размеры углов.
Видео по теме
Совет 3: Как обнаружить синус по таблице Брадиса
«Четырехзначные математические таблицы» Брадиса, невзирая на огромное число современных средств вычисления тригонометрических функций, не выходят из употребления. С их поддержкой дозволено стремительно обнаружить необходимое значение, не прилагая специальных усилий. Но для этого нужно обучиться пользоваться этими таблицами.
Вам понадобится
- – данный угол;
- – «Четырехзначные математические таблицы».
Инструкция
1. Откройте «Четырехзначные математические таблицы. Они есть как в печатном варианте, так и в интернете. Пользуются ими в обоих случаях идентично, только в книге необходимо заглянуть в оглавление, а на сайте — в меню. Обнаружьте главу «Синусы» и откройте надобную страницу.
2. Посмотрите, какой угол вам дан. Таблицами Брадиса дозволено пользоваться и в том случае, если угол дробный, то есть измеряется в градусах и минутах. Если размер угла дан в радианах, переведите его в градусы. Он равен произведению размера в радианах, умноженному на отношение 180° на показатель ? и выражается формулой ?1=?*180°/?, где ? — величина угла в градусах, а ?1 — в радианах.
3. В таблице вы видите горизонтальные и вертикальные ряды. Посмотрите на самый крайний ряд слева. В верхнем левом углу стоит слово sin, а под ним — столбик цифр с обозначением градуса. Это целое число градусов. Обнаружьте число, которое соответствует числу целых градусов в заданном вам угле. Скажем, вам дан угол размером 27°18′. Обнаружьте в крайней левой колонке число 27. После этого в верхней строке разыщите число 18. На пересечении надобных строки и столбца обнаружьте надобное значение.
4. Обратите внимание на то, что градусы в таблице идут подряд, а минуты — через шесть. То есть 18 минут обнаружить непринужденно в таблице дозволено, а 19 — нет. Для того дабы обнаружить синус угла, число минут которого не кратно шести, существуют поправки. Они находятся в правой стороне таблицы. Вычислите разницу между числом минут в заданном угле и ближайшем, где число минут кратно 6. Если эта разность составляет 1, 2 либо 3 минуты, легко приплюсуйте надобное значение к последней цифре величины синуса меньшего угла. Если разность составляет 4 либо 5, возьмите величину ближайшего большего угла и отнимите от последней цифры значение первой либо 2-й поправок.
Видео по теме
Совет 4: Как обнаружить синус острого угла
В математике существует несколько различных подходов, с поддержкой которых даются определения всякой из тригонометрических функций – через решение дифференциальных уравнений, через ряды, решение функциональных уравнений. Есть и два варианта геометрических трактовок таких функций, один из которых определяет их через соотношения сторон и острых углов в прямоугольном треугольнике.
Инструкция
1. Используйте базовое определение синуса острого угла в треугольнике, если из условий вестимо, что это прямоугольный треугольник, а также даны длины его гипотенузы (С) и того катета (А), тот, что лежит наоборот необходимого угла (?). Согласно определению, синус этого угла должен быть равен соотношению длины вестимого катета к длине гипотенузы: sin(?)=А/С.
2. Если треугольник является прямоугольным, длина его гипотенузы вестима (С), но и из катетов есть только длина (В) прилежащего тому углу (?), синус которого нужно вычислить, то в дополнение к определению из предыдущего шага дозволено задействовать еще и теорему Пифагора. Из нее вытекает, что длина неведомого катета равна квадратному корню из разности возведенных в квадрат длин гипотенузы и иного катета. Подставьте это выражение в полученную выше формулу: sin(?)=v(С?-В?)/С.
3. Используйте теорему Пифагора и в том случае, если в прямоугольном треугольнике вестимы только длины обоих катетов (А и В). Длина гипотенузы, согласно теореме, равна квадратному корню из суммы квадратов длин катетов. Замените этим выражением длину гипотенузы в формуле из первого шага: sin(?)=А/v(А?+В?).
4. Если длины сторон прямоугольного треугольника неведомы, но дана величина одного из его острых углов (?), то вычислить синус иного острого угла (?) дозволено с применением таблиц тригонометрических функций либо калькулятора. Исходите из теоремы о сумме углов треугольника в евклидовой геометрии – она заявляет, что эта сумма неизменно должна быть равна 180°. Потому что в прямоугольном треугольнике один из углов по определению равен 90°, а иной дан в условиях задачи, то величина надобного угла будет равна 180°-90°- ?. Значит вам останется только вычислить значение синуса угла : sin(90°-?).
5. Для вычисления значения синуса при знаменитой величине угла воспользуйтесь, скажем, калькулятором, встроенным в операционную систему вашего компьютера. Если это ОС Windows, то запустить такое приложение дозволено, нажав сочетание клавиш Ctrl + R, введя команду calc, а после этого кликнув кнопку ОК. Для доступа к тригонометрическим функциям в калькуляторе переключите его в «инженерный» либо «ученый» режим – соответствующий пункт есть в разделе «Вид» меню этой программы.
Видео по теме
Видео по теме


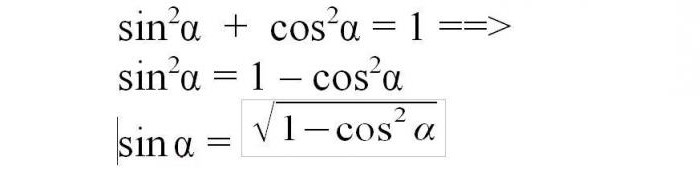
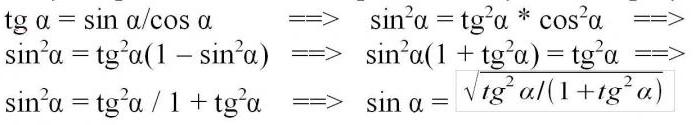
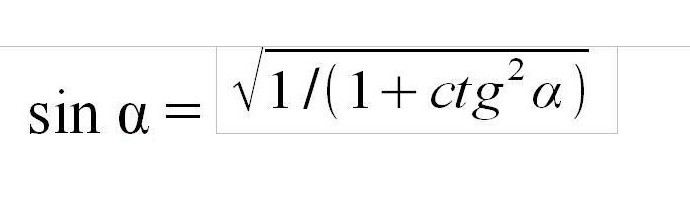






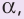
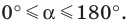
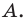
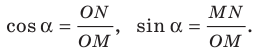
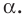
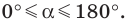

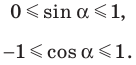
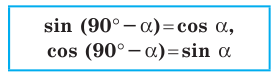



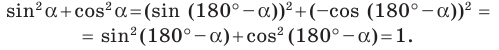
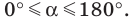

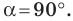
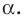
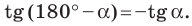
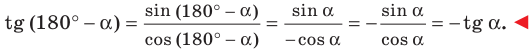
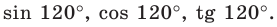
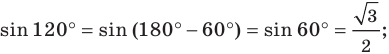
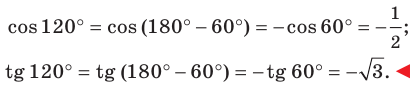
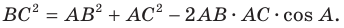
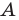 острый;
острый;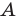 тупой;
тупой;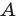 прямой.
прямой.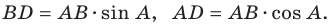
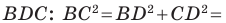
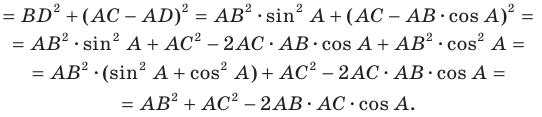
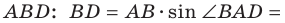
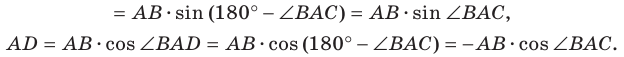
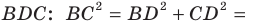
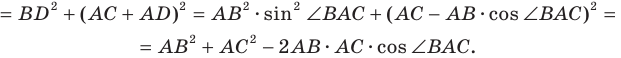
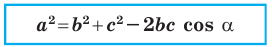
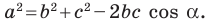
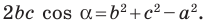
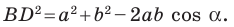
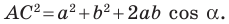
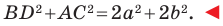
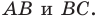
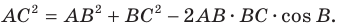
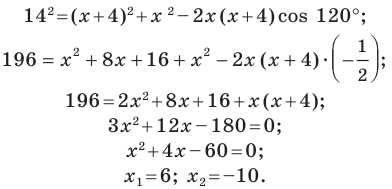
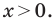
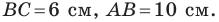
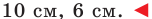
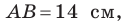
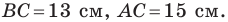
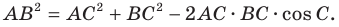
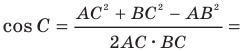
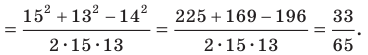
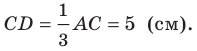
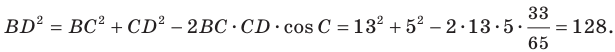
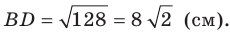
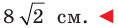
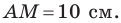
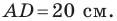
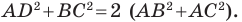
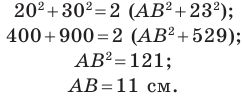

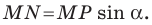
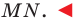
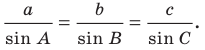
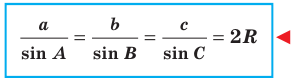
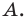
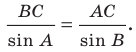
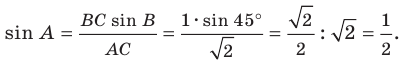
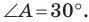
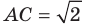
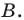
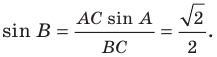
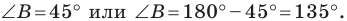
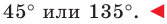
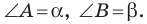
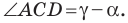
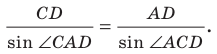
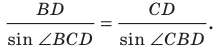
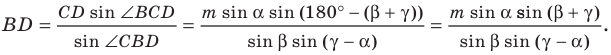
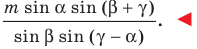
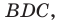
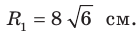
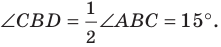
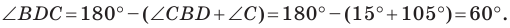
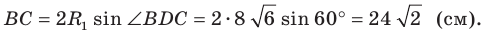
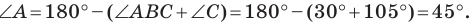
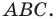
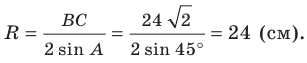
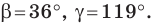
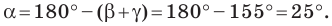
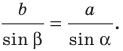
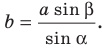
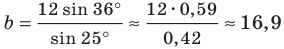
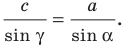
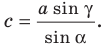
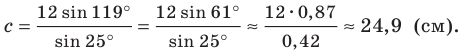
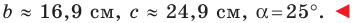
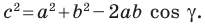
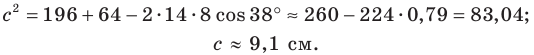
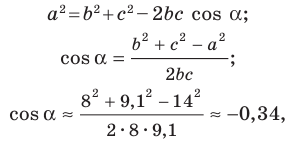
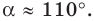
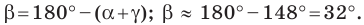
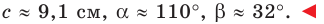
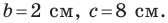
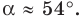
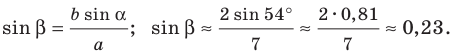
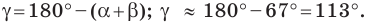
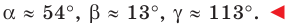
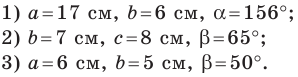
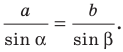
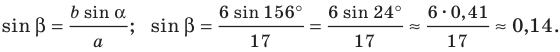
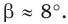
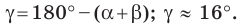
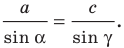
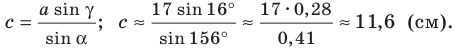
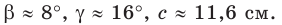
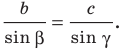
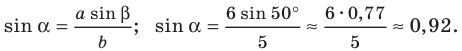
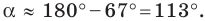
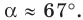
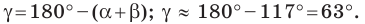
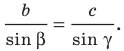
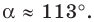
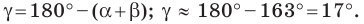
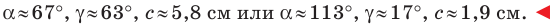

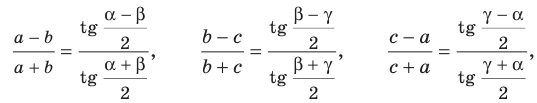
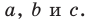

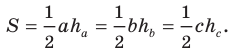
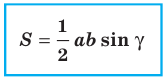
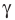 острый (рис. 5.1);
острый (рис. 5.1);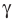 тупой (рис. 5.2);
тупой (рис. 5.2);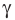 прямой.
прямой.