Задания
Версия для печати и копирования в MS Word
Задания Д13 № 318479
В прямоугольном параллелепипеде известны длины рёбер
Найдите синус угла между прямыми CD и
Решение.
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном параллелепипеде известны длины рёбер
Найдите синус угла между прямыми CD и
Отрезки DC и D1C1 лежат на параллельных прямых, поэтому искомый угол между прямыми A1C1 и DC равен углу между прямыми A1C1 и D1C1.
Из прямоугольного треугольника A1C1D1 по получаем:
Тогда для угла A1C1D1 имеем:
Ответ: 0,6.
Аналоги к заданию № 318474: 318477 318479 318481 … Все
Прототип задания
Условие
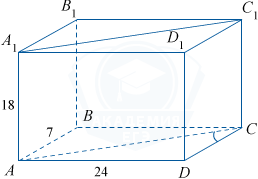
Прямоугольный параллелепипед имеет следующие длины ребер AB=7, AD=24, AA_1=18. Найдите синус угла между прямыми CD и A_1C_1.
Показать решение
Решение
Рассмотрим рисунок:
Угол между прямыми DC и A_1C_1 совпадает с углом между прямыми DC и AC, так как AC parallel A_1C_1.
sinangle ACD= frac{AD}{AC}= frac{24}{sqrt{24^2+7^2}}= frac{24}{sqrt{625}}= frac{24}{25}= 0,96.
Ответ
0,96
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Рассказать друзьям
Лучшие онлайн-курсы для подготовки к ЕГЭ
Лучшие репетиторы для сдачи ЕГЭ
Комментарии
Задавайте ваши вопросы и помогайте друг другу в решении задач
Комментарии содержащие в себе рекламу, нецензурную лексику и не относящиеся к тематике сайта будут удалены
Лучшие репетиторы для сдачи ЕГЭ
Перед вами очередная статья с параллелепипедами. Представленные задания просты, вычислений никаких нет или их минимум. Рассматриваются кубы и прямоугольные параллелепипеды. Важно грамотно выполнить построения и знать элементарные свойства. Например, в данных заданиях используются:
1. В равностороннем треугольнике все его углы равны 60 градусам.
2. Диагонали граней куба равны.
3. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
4. Необходимо понимание понятия — скрещивающиеся прямые.
Напомню какая призма является правильной.
Правильная призма – это призма основания которой — правильные многоугольники, боковые рёбра расположены под прямым углом к основаниям. Например, правильная треугольная призма – это прямая призма, основания которой равносторонние треугольники.
Правильная четырёхугольная призма – это прямая призма, основания которой являются квадратами. Понятно, что такая призма является прямоугольным параллелепипедом.
Правильная шестиугольная призма – это прямая призма, основания которой являются правильными шестиугольниками. Рассмотрим задачи:
315130. В кубе ABCDA1B1C1D1 точка К — середина ребра АA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Построим куб, обозначим его вершины и точки K, M и L.
Так как данные точки являются серединами ребёр, то отрезки KM, ML, KL будут равны между собой. Это означает, что треугольник KML равносторонний. Известно, что в равностороннем треугольнике его углы равны по 60 градусов. Таким образом, угол MLK равен 600.
Ответ: 60
316554. В кубе ABCDA1B1C1D1 найдите угол между прямыми АD1 и B1D1. Ответ дайте в градусах.
Построим куб, обозначим вершины и данные отрезки, также построим отрезок АВ1.
Отрезки АD1, B1D1 и АD1 являются диагоналями граней куба, то есть все они равны, значит треугольник АD1B1 является равносторонним. Известно, что в равностороннем треугольнике его углы равны по 60 градусов.
Таким образом, угол между прямыми АD1 и B1D1 равен 600.
Ответ: 60
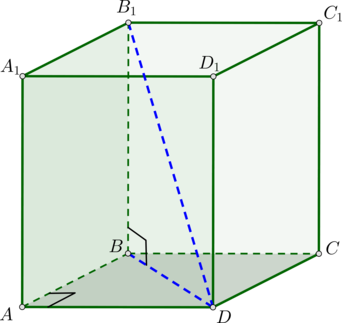
318474. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1.
Построим отрезки CD и A1C1:
В данной задаче имеем скрещивающиеся прямые, то есть сами они не имеют общей точки пересечения. Но этот угол между скрещивающимся прямыми определяется. Как?
Простыми словами: если вы мысленно представите в пространстве две непараллельные прямые, то всегда существует такой перпендикуляр, который их соединяет. Так вот, если мы параллельным переносом сдвинем одну прямую к другой по этому перпендикуляру до пересечения этих прямых, то полученный между ними угол и будет тем самым искомым углом.
В кубах и параллелепипедах, где прямые проходят через рёбра и диагонали такие углы определить несложно. А вот в части С присутствуют задания со скрещивающимися прямыми на порядок сложнее.
Вернёмся к нашей задаче.
Мысленно сдвинем отрезок CD вдоль перпендикуляра СC1 до пересечения с прямой A1C1. Получается, что необходимо найти синус угла между A1C1 и C1D1. Это мы можем сделать воспользовавшись определением синуса в прямоугольном треугольнике А1C1D1. Найдём:
По определению синуса:
Ответ: 0,6
318475. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что AC1 = 2BC. Найдите острый угол между диагоналями BD1 и CA1. Ответ дайте в градусах.
Построим правильную четырёхугольную призму, обозначим вершины, построим диагонали BD1 и CA1:
Сразу отметим, что диагонали BD1 и CA1 являются диагоналями прямоугольника A1BCD1, то есть они равны между собой и равны диагонали AC1 (так как призма правильная четырехугольная).
Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, то есть:
A1С = D1B
A1O = ОС и D1O = ОB
A1O = ОС = D1O = ОB
В условии сказано, что AC1 = 2BC, значит имеем BD1 = CA1 = 2BC. На основании изложенного можем сделать вывод о том, что:
BO = ОС = BC и A1O = ОD1 = A1D1
то есть треугольники BОС и A1OD1 равносторонние.
Таким образом, угол острый между диагоналями равен 600.
Ответ: 60
В данных заданиях используется теорема Пифагора, для нахождения углов необходимо владеть понятиями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике.
245359. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Посмотреть решение
245360. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Посмотреть решение
245361. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Посмотреть решение
245362. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Посмотреть решение
245363. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Посмотреть решение
284357. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 3, CD = 2, AD = 2. Найдите длину ребра AA1.
Посмотреть решение
284363. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Ответ:параллельны
Объяснение:
может быть что-то такое
Решение в скане…………..
Ответ:
Объяснение:#1 за допомогою кутника накреслить перпендикуляр на відстані 2,4 см ( середина)
#2 усередині
#3 на одній із сторін
#4 медіана ділить сторону( основу) навпіл, отже половини основ будуть рівні, тоді ребра також будуть рівні, бо виходять із однієї точки і закінчуються на рівних половинах основи
ΔRKT∞ΔRET (<R общий и <RKE=<KTE по условию)
Следовательно RT/RK=KT/KE=RK/RE
17/10=10/RE
RE=100/17=5 15/17
<AME=90⇒x=ME=√(AE²-AM²)=√(169-25)=√144=12
ΔMAE∞ΔCAB (<A-общий и <AME=<ACB по условию)
AM/AC=ME/CB
5/(5+10)=12/y
y=(15*12)/5=36
Тема 2.
Геометрия в пространстве (стереометрия)
2
.
10
Прямоугольный параллелепипед
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
Решаем задачи
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен
48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Показать ответ и решение
Объём прямоугольного параллелепипеда равен произведению всех трёх его измерений. Из вершины выходит по одному
ребру каждого из измерений. Пусть длина неизвестного ребра равна . Тогда
Дан прямоугольный параллелепипед с ребрами и
. Найдите его диагональ.
Показать ответ и решение
Пусть .
По теореме Пифагора из прямоугольного треугольника (
) имеем:
.
Из прямоугольного треугольника (
) по теореме Пифагора
.
Подставляя из первого равенства во второе, получим:
Показать ответ и решение
Так как то
По теореме
Пифагора
Следовательно,
Показать ответ и решение
Искомый объем равен половине объема прямоугольного параллелепипеда
следовательно, он равен
Показать ответ и решение
Многогранник, объем которого необходимо найти, является прямоугольной
треугольной пирамидой, высота которой равна а основание представляет
собой прямоугольный треугольник Следовательно, этот объем равен
В прямоугольном параллелепипеде известно, что
Найдите длину диагонали
Показать ответ и решение
В прямоугольном параллелепипеде с измерениями
и
длина его диагонали
равна
Следовательно,
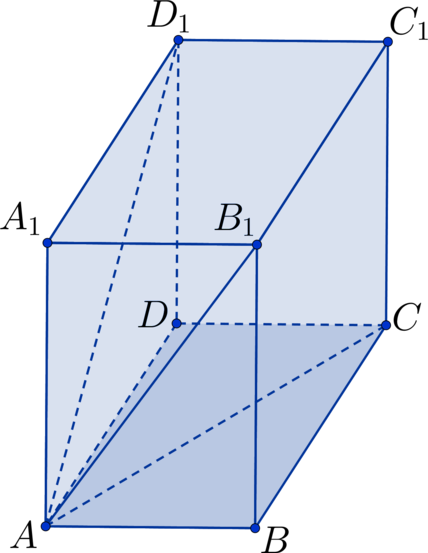
От прямоугольного параллелепипеда отсекли многогранник, вершинами которого являются точки
Найдите объём оставшейся части, если объём отсечённой части равен 8.
Показать ответ и решение
Запишем выражение для объёма пирамиды который по условию равен 8:
Заметим, что Найдём объём всего параллелепипеда:
Тогда объём оставшейся части равен
Показать ответ и решение
Способ 1.
Заметим, что объем многогранника, вершинами которого являются
точки в два раза меньше объема прямоугольного
параллилепипеда, поскольку это призма с основанием, в два раза меньше, чем у
параллелепипеда.
Тогда — искомый объём,
— объём параллелепипеда:
Способ 2.
Полученный многогранник представляет из себя прямую призму с основаниями
и
объём которой вычисляет ся по формуле
Дан прямоугольный параллелепипед . Во сколько раз объем пирамиды
меньше объема этого параллелепипеда?
Показать ответ и решение
Пусть ,
,
. Тогда объем параллелепипеда равен
Так
как (потому что по определению прямоугольного параллелепипеда в основании
лежит прямоугольник), то объем пирамиды
Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
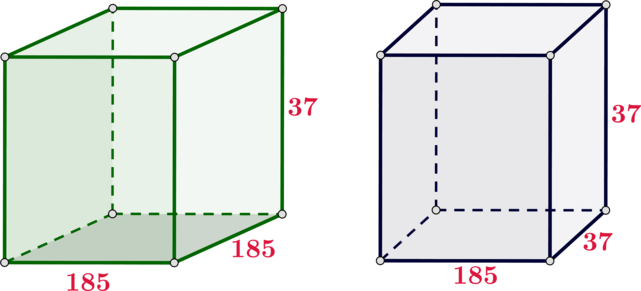
Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185, 37 и 37. Во сколько раз
объем первого параллелепипеда больше объема второго параллелепипеда?
Показать ответ и решение
Отношение их объемов равно:
В прямоугольном параллелепипеде :
,
,
. Чему равна
сумма всех ребер параллелепипеда?
Показать ответ и решение
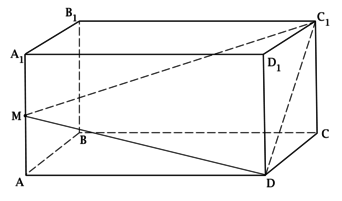
Так как – прямоугольный параллелепипед, то
– проекция
на
, тогда по теореме Пифагора
при
этом по теореме Пифагора
откуда
Так как – прямоугольный параллелепипед, то по теореме Пифагора
Аналогично по теореме Пифагора
Таким образом,
тогда
Показать ответ и решение
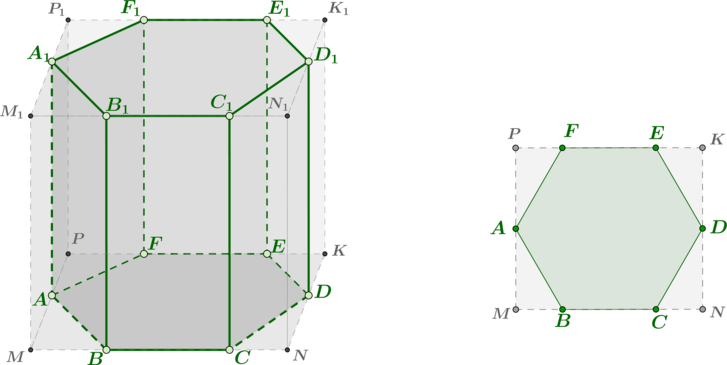
Рассмотрим картинку. Так как параллелепипед прямоугольный, то он прямой и в основании лежит
прямоугольник. Следовательно, его боковые ребра (например, ) параллельны боковым ребрам
призмы и равны, так как основания призмы вписаны в основания параллелепипеда (то есть лежат в
одних и тех же плоскостях). Отсюда следует, что высоты призмы и параллелепипеда одинаковы. Пусть
– длина их высоты.
Рассмотрим отдельно основание. По свойству правильного шестиугольника . Так как
– прямоугольник, то есть
, то
. Заметим также, что вообще говоря
, а
.
Пусть – сторона шестиугольника. Его угол равен
, следовательно, по теореме косинусов:
Заметим также, что , следовательно, в треугольнике
:
Следовательно, .
Значит, – прямоугольник со сторонами
и
.
Площадь правильного шестиугольника равна , следовательно, объем призмы
а
объем параллелепипеда
Следовательно,
Показать ответ и решение
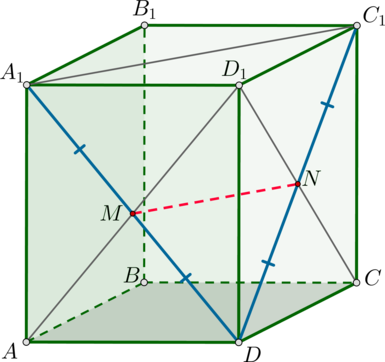
Так как , то грани
и
равны, следовательно, и их диагонали
равны, значит, . Так как диагонали прямоугольника точкой пересечения делятся
пополам, то . Рассмотрим
: в нем
является средней
линией, следовательно, она равна половине основания , которое в свою очередь является
диагональю квадрата , следовательно, равно
. Следовательно,
.
Показать ответ и решение
Площадь полной поверхности первого параллелепипеда
Площадь полной поверхности второго параллелепипеда
Следовательно,