Свойства тригонометрических функций
Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:
$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$
Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.
Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:
$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$
А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$
Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$
Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$
А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:
$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$
Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.
И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.
И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.
Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$
Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.
Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.
Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)
Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:
$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.
Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)
Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:
Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)
Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс — это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$
Ответ:(сtg(alpha)=pm2sqrt{2}).
Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.
Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.
Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.
Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:
Пример 2
По рисунку определить значение (sin(alpha)=?)
По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$
Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)
Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:
Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.
Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$
У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.
Ответ: (cos(alpha)=frac{1}{2}.)
Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).
Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$
А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$
Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)
Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.
Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$
Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли — выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$
Ответ: (AB=10;) (BC=5*sqrt{3}.)
Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.
Рассмотрим задачу посложнее.
Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).
Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим — сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:
$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$
Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.
Следующий важный момент, на который следует обратить внимание — это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$
Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!
Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!
А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$
В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.
Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.
С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$
Ответ: (AH=12,5.)
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
- Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
[ sin x=frac{a}{c} ; cos x=frac{b}{c} ; operatorname{tg} x=frac{sin x}{cos x} ; operatorname{ctg}=frac{1}{operatorname{tg} x}=frac{sin x}{cos x} ]
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1.синуса (sin):
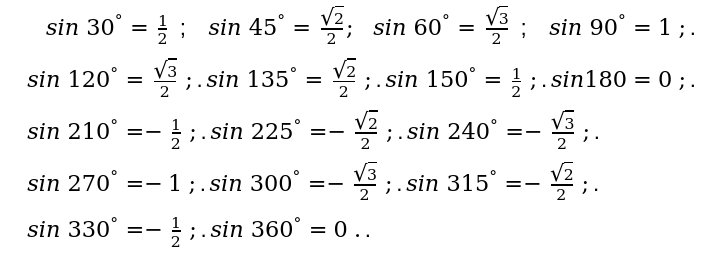
2. косинуса (cos):
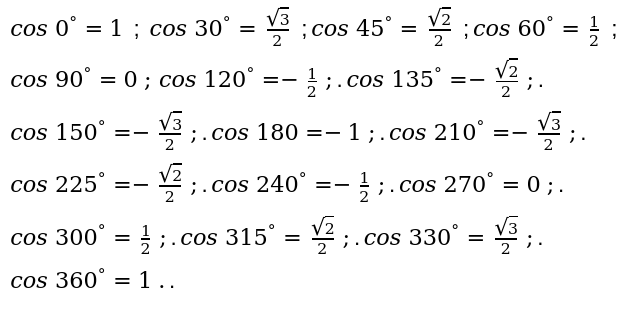
3. тангенса(tg):
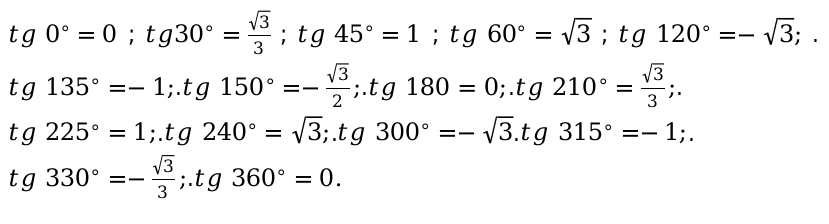
[ operatorname{tg} 90^{circ}, 270^{circ} ]
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.
4. котангенса (ctg)
[ operatorname{ctg} 0^{circ}, 180^{circ}, 360^{circ} ]
Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
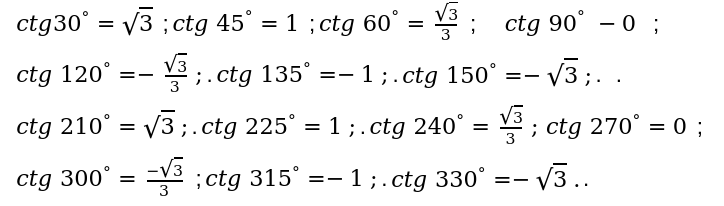
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
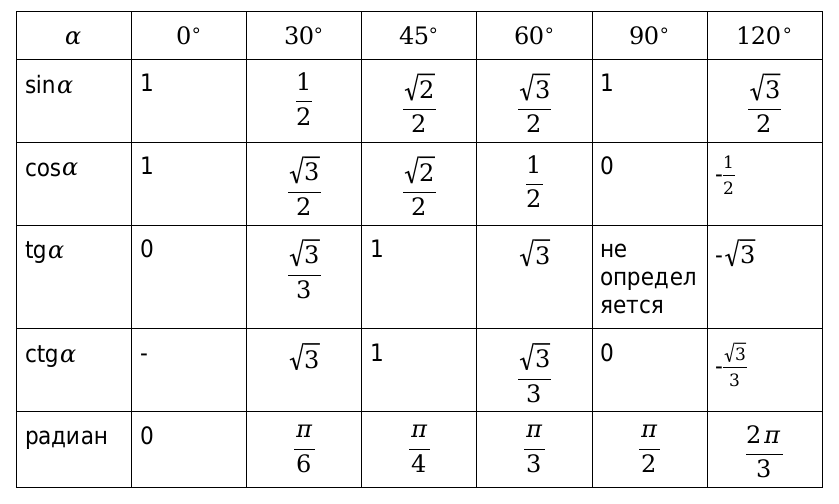
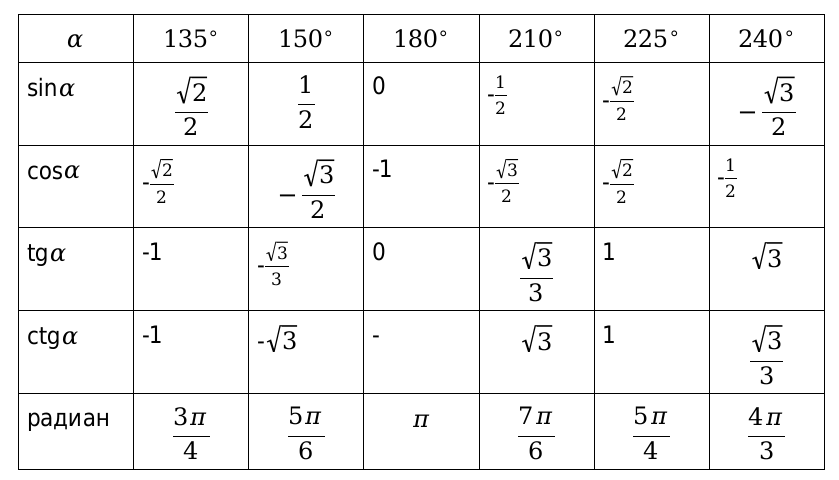
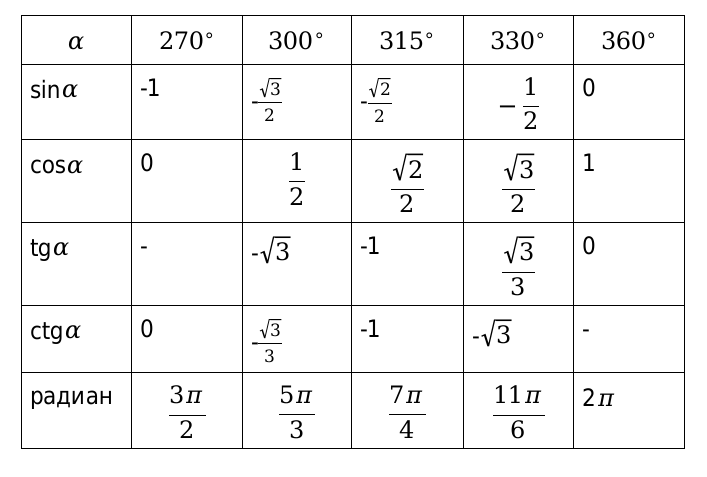
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
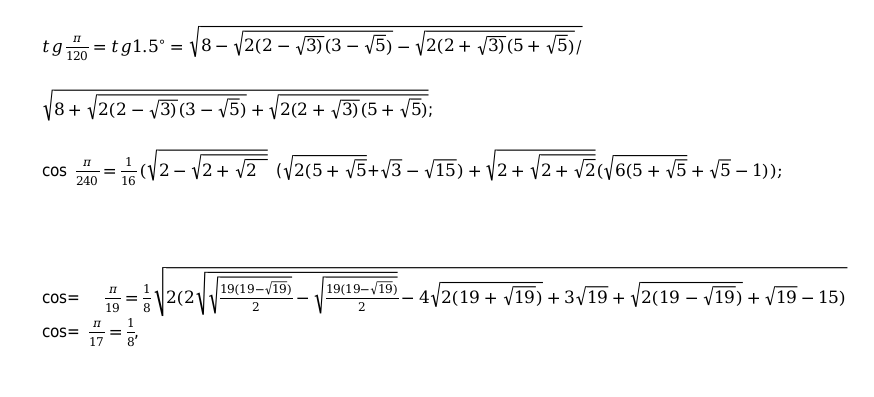
Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.
Пример №1. Необходимо определить чему равен [operatorname{tg} 300]
Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.
Следовательно:[operatorname{tg} 300^{circ}=-sqrt{3}].
Пример №2. Необходимо определить чему равен [cos frac{5 pi}{3}].
Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.
[text { Следовательно: } operatorname{tg} 300^{circ}=frac{1}{2} .]
Пример №3. Необходимо определить чему равен [cos frac{11 pi}{6}].
Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.
[text { Следовательно } cos =frac{sqrt{3}}{2}=330^{circ}.]
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут. Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0.6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 . 6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение [frac{sqrt{x}}{2}] и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя [frac{sqrt{x}}{2}] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении [frac{sqrt{x}}{2}] записываем значение угла.
Получаем следующую запись: [frac{sqrt{x}}{2}=frac{0}{2}=0]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
[ frac{sqrt{1}}{2}=frac{1}{2} ; frac{sqrt{2}}{2}=frac{(sqrt{2 cdot 2})}{(2 cdot sqrt{2})}=frac{2}{2 cdot sqrt{2}}=frac{1}{sqrt{2}} ; frac{sqrt{3}}{2} frac{sqrt{4}}{2}=frac{2}{2}=1 ]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.
4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. [operatorname{tg}=frac{sin }{cos }]. Выходим что искомое значение равно данному выражению. Если [operatorname{tg} 45^{circ}=frac{sin }{cos }=frac{sqrt{1}}{2} / frac{sqrt{3}}{2}=frac{1}{sqrt{3}} .]
Аналогично поступаем и далее.
5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.
[text { Так как, } operatorname{cosec}=frac{1}{sin } . text { Например, } sin 40^{circ}=frac{1}{2}, text { поэтому } operatorname{cosec} 40^{circ}=frac{1}{frac{1}{2}}=2]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
[text { Таким же методом заполняются оставшиеся строки таблицы. Так } text { как } operatorname{ctg}=frac{1}{t g}, text { в свою очередь } operatorname{ctg}=frac{cos }{sin }]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin[45^{circ}=frac{4}{6}=0,67]
Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится [operatorname{cosec}=frac{1}{sin }] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету [mathrm{sec}=frac{1}{cos }].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.
[ cos (alpha+360 cdot n)=sin alpha ;] [ sin (alpha+360 cdot n)=sin alpha / ]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
[ operatorname{tg} alpha=frac{sin alpha}{cos alpha} ; operatorname{ctg} alpha=frac{cos alpha}{sin alpha} ]
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
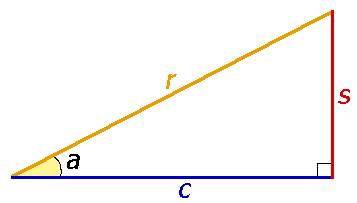
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| sin | 0 |
|
|
|
1 |
| cos | 1 |
|
|
|
0 |
| tg | 0 |
|
1 | √3 | – |
| ctg | – | √3 | 1 |
|
0 |
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π.
Например, для угла 90° будет
- 90°
- 180°
· π =
- 1
- 2
π
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
 |
Онлайн тренажер
|
Простые тригонометрические тождества
Используя вышеописанные формулы:
тангенс угла выражается через отношение синуса к косинусу:
tg(a) =
- s
- c
=
- sin(a) · r
- cos(a) · r
=
- sin(a)
- cos(a)
;
Соответственно котангенс выражается аналогично:
ctg(a) =
- c
- s
=
- cos(a) · r
- sin(a) · r
=
- cos(a)
- sin(a)
;
Также можно заметить, что произведение тангенса на котангес равно единице:
tg(a) · ctg(a) =
- sin(a)
- cos(a)
·
- cos(a)
- sin(a)
=
- sin(a) · cos(a)
- cos(a) · sin(a)
= 1
Иными словами, тангенс угла обратно пропорционален котангенсу угла и наоборот:
tg(a) · ctg(a) = 1
;
tg(a) =
- 1
- ctg(a)
;
сtg(a) =
- 1
- tg(a)
Используя теорему Пифагора в треугольнике, что сумма квадратов катетов равно квадрату гипотенузы
r2 = s2 + c2 = (sin(a) · r)2 + (cos(a) · r)2;
r2 · (sin(a)2 + cos(a)2) = r2
Сократим обе части на r2, получим:
sin2a + cos2a = 1
Разделив обе части на квадрат синуса или квадрат косинуса, получим еще два основных тригонометрических тождества:
1 + tg2a =
- 1
- cos2a
;
1 + ctg2a =
- 1
- sin2a
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023