Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
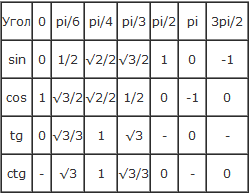
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
Summary :
The sin trigonometric function to calculate the sin of an angle in radians,
degrees or gradians.
sin online
Description :
Sine function
The calculator allows to use most of the trigonometric functions, it is possible to calculate the
sine,
the cosine
and the tangent
of an angle through the functions of the same name..
The trigonometric function sine noted sin,
allows to calculate
the sine of an angle online , it is possible to use different angular units :
degree, grade and radians wich is the angular unit by default.
- Calculation of the sine
- Special sine values table
- Main properties
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x)`
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x)`
- Derivative of sine
- Antiderivative of sine
- Properties of the sine function
- Equation with sine
Sine calculating an angle in radians
The sine calculator allows through the sin function to calculate
online the sine sine of an angle in radians, you must first
select the desired unit by clicking on the options button calculation module.
After that, you can start your calculations.
To calculate sine online of `pi/6`, enter
sin(`pi/6`), after calculation, the result
`1/2` is returned.
Note that the sine function is able to recognize some special angles and make the
calculations with special associated values in exact form.
Calculate the sine of an angle in degrees
To calculate the sine of an angle in degrees, you must first select the desired unit
by clicking on the options button calculation module. After that, you can start your calculus.
To calculate sine of 90, enter sin(90), after calculation, the
restults 1 is returned.
Calculate the sine of an angle in gradians
To calculate the sine of an angle in gradians, you must first select the desired unit
by clicking on the options button calculation module. After that, you can start your calculus.
To calculate sine of 50, enter sin(50), after computation,
the result `sqrt(2)/2` is returned.
Note that the sine function is able to recognize some special angles and do the
calculus with special associated exact values.
The sine admits some special values which the calculator is able to determine in exact forms. Here is a table of
the commonsine values:
| sin(`2*pi`) | `0` |
| sin(`pi`) | `0` |
| sin(`pi/2`) | `1` |
| sin(`pi/4`) | `sqrt(2)/2` |
| sin(`pi/3`) | `sqrt(3)/2` |
| sin(`pi/6`) | `1/2` |
| sin(`2*pi/3`) | `sqrt(3)/2` |
| sin(`3*pi/4`) | `sqrt(2)/2` |
| sin(`5*pi/6`) | `1/2` |
| sin(`0`) | `0` |
| sin(`-2*pi`) | `0` |
| sin(`-pi`) | `0` |
| sin(`pi/2`) | `-1` |
| sin(`-pi/4`) | `-sqrt(2)/2` |
| sin(`-pi/3`) | `-sqrt(3)/2` |
| sin(`-pi/6`) | `-1/2` |
| sin(`-2*pi/3`) | `-sqrt(3)/2` |
| sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x in RR, k in ZZ`,
The derivative of the sine is equal to cos(x).
The antiderivative of the sine is equal to -cos(x).
The sine function is an odd function, for every real x, `sin(-x)=-sin(x)`.
The consequence for the curve representative of the sine function is that it admits the origin of the reference point as point of symmetry.
The calculator has a solver which allows it to solve
equation with sine
of the form cos(x)=a.
The calculations to obtain the result are detailed, so it will be possible to solve equations like
`sin(x)=1/2`
or
`2*sin(x)=sqrt(2)`
with the calculation steps.
Syntax :
sin(x), where x is the measure of an angle in degrees, radians, or gradians.
Examples :
sin(`0`), returns 0
Derivative sine :
To differentiate function sine online, it is possible to use the derivative calculator which allows the calculation of the derivative of the sine function
The derivative of sin(x) is derivative(`sin(x)`)=`cos(x)`
Antiderivative sine :
Antiderivative calculator allows to calculate an antiderivative of sine function.
An antiderivative of sin(x) is antiderivative(`sin(x)`)=`-cos(x)`
Limit sine :
The limit calculator allows the calculation of limits of the sine function.
The limit of sin(x) is limit(`sin(x)`)
Inverse function sine :
The inverse function of sine is the arcsine function noted arcsin.
Graphic sine :
The graphing calculator is able to plot sine function in its definition interval.
Property of the function sine :
The sine function is an odd function.
Calculate online with sin (sine)
В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Но если Вам нужно рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″
или -1775° 15′ 22″ ), то можно воспользоваться тригонометрическим калькулятором.
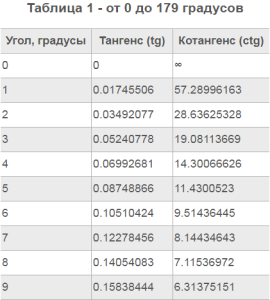
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | 0.8571673 | -0.51503807 |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
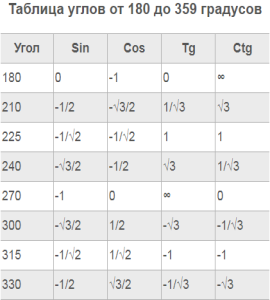
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Другие таблицы
Таблица синусов.
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — синус угла
sin(°) = 0
Калькулятор — арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-sinusov — uchim.org
Таблица синусов для 0°-180°
|
|
|
|
Таблица синусов для 181°-360°
|
|
|
|
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Как легко запомнить таблицу синусов (видео)
Таблицу важно всегда помнить на алгебре, чтобы найти синус.
Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)