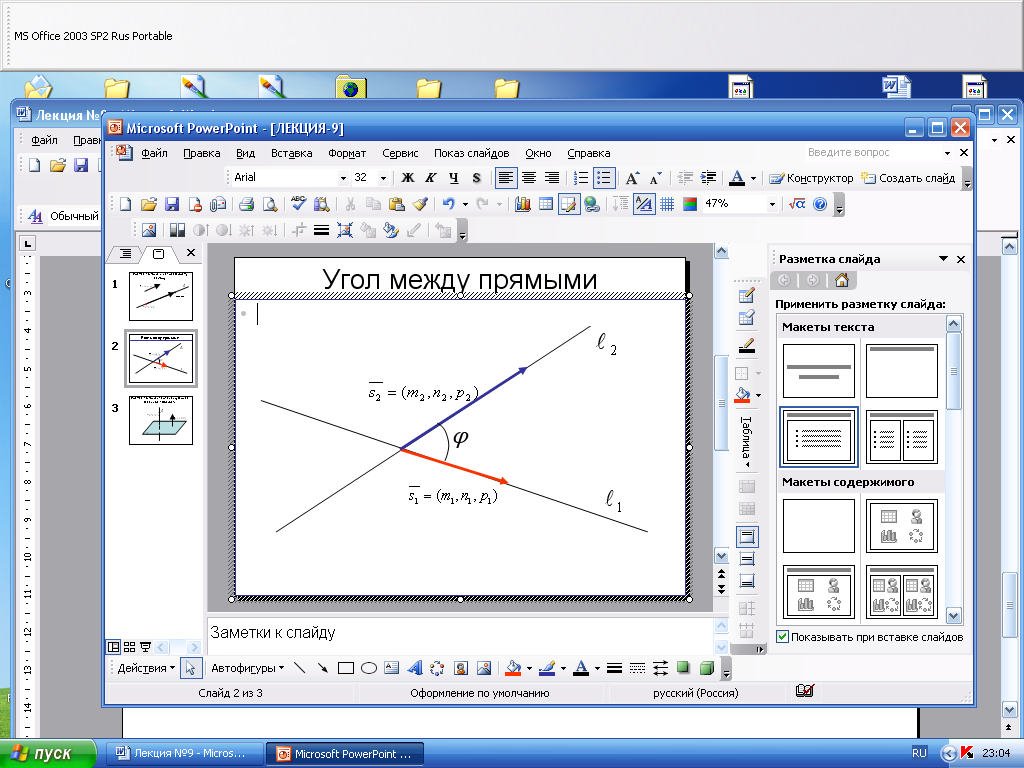
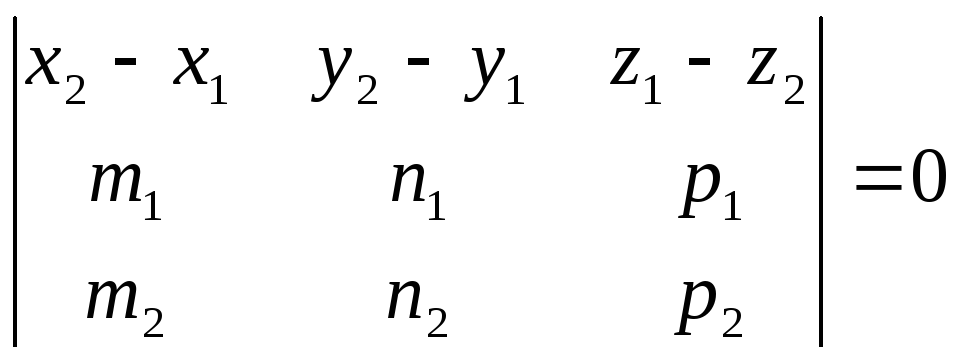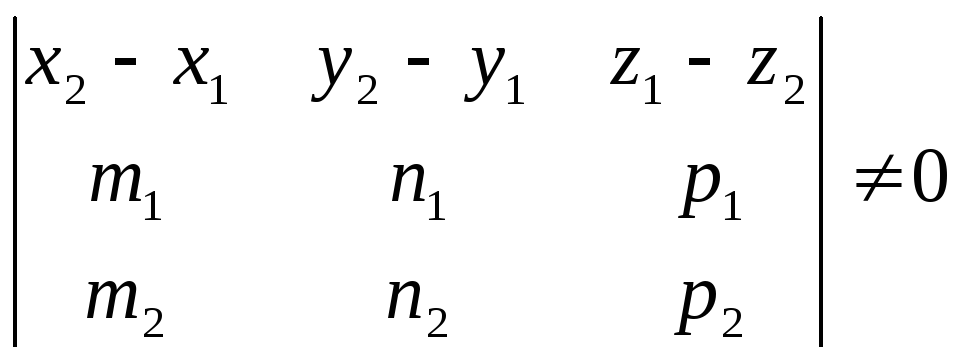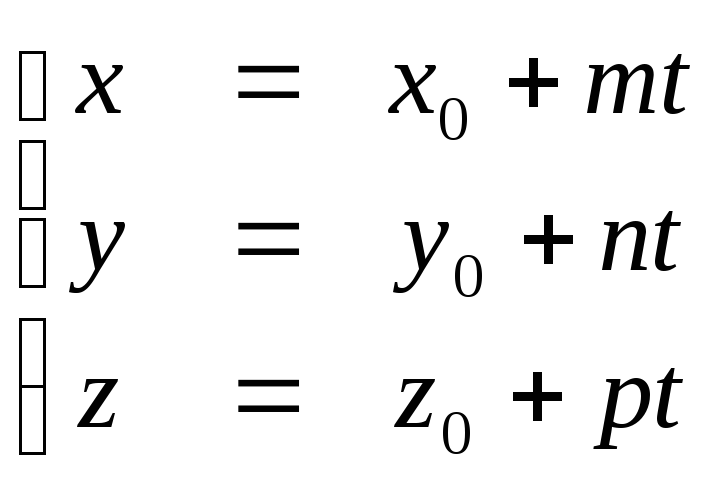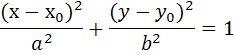Угол между прямыми в пространстве
Пусть
две прямые
и
заданы каноническими уравнениями:
:
и
:
.
Выпишем направляющие
векторы этих прямых:
,
.
Угол
между прямыми равен углу между их
направляющими векторами:
.
Для нахождения острого угла между
прямыми, числитель правой части следует
взять по модулю.
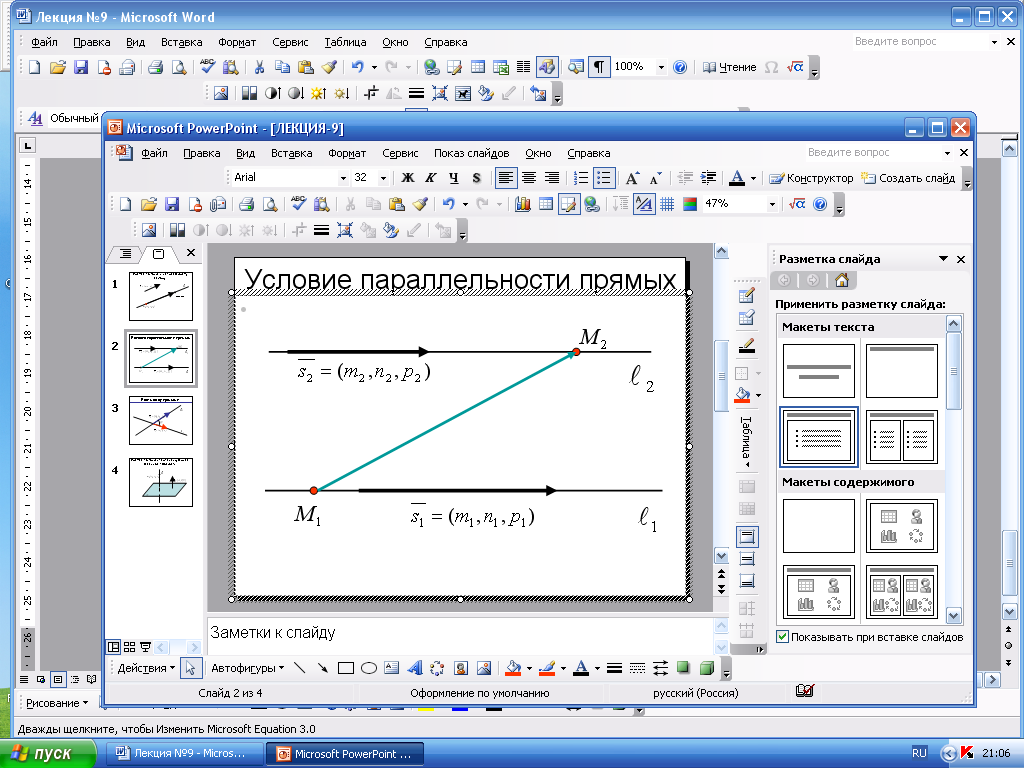
Взаимное расположение прямых в пространстве
Пусть две прямые
в пространстве заданы каноническими
уравнениями:
:
и
:
их направляющие векторы соответственно:
и
.
Точка
принадлежит
прямой
,
а точка
принадлежит
.Составим
вектор
.
По взаимному расположению векторов
можно
судить о взаимном расположении прямых:
Прямые
параллельны,
если
и
коллинеарны и
не
параллелен
Д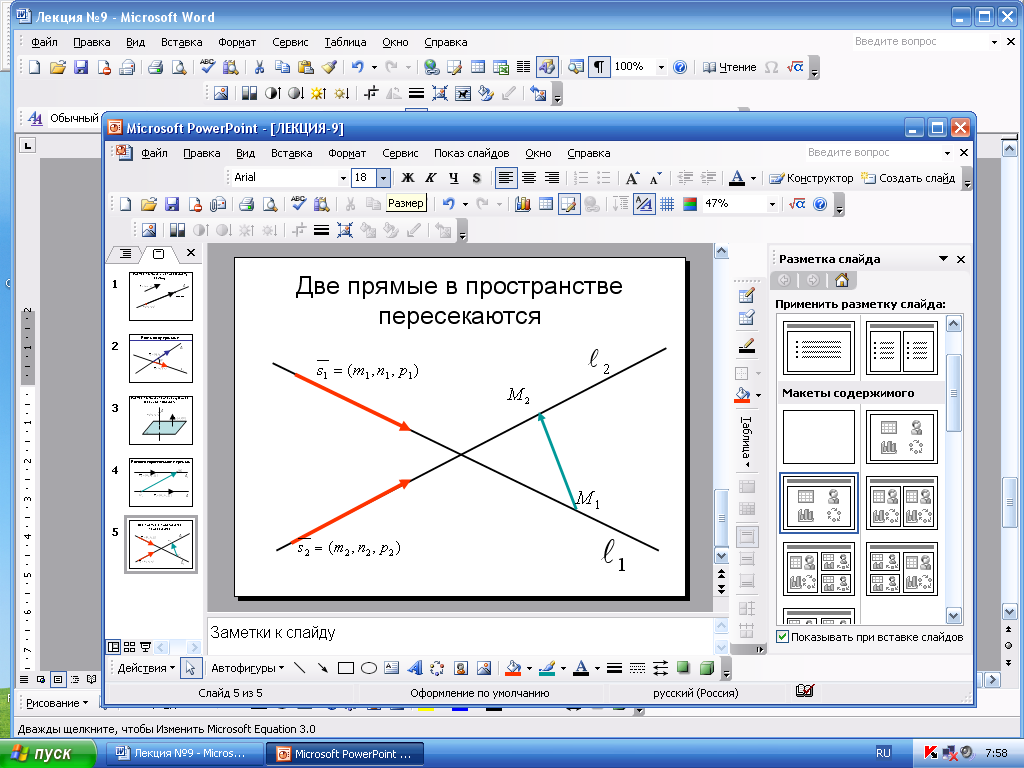
прямые пересекаются в пространстве,
если
и
не
коллинеарны, а векторы
,
и
компланарны., т.е. их смешанное произведение
равно нулю:
Д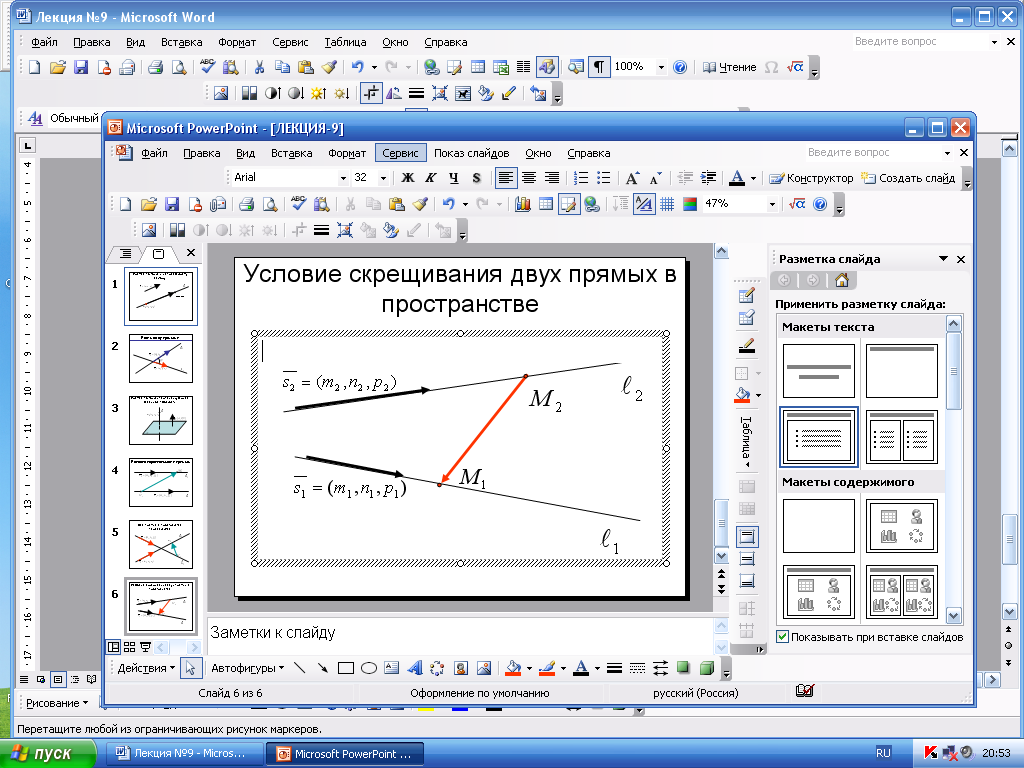
прямые скрещиваются,
если векторы
,
и
не компланарны, т.е. их смешанное
произведение не равно нулю.
Угол между прямой и плоскостью
Пусть
плоскость
задана своим общим уравнением:
Ax+By+Cz+D=0,
а прямая
в каноническом виде:
.
Углом между прямой и плоскостью называется
угол между прямой и ее проекцией на
плоскость.
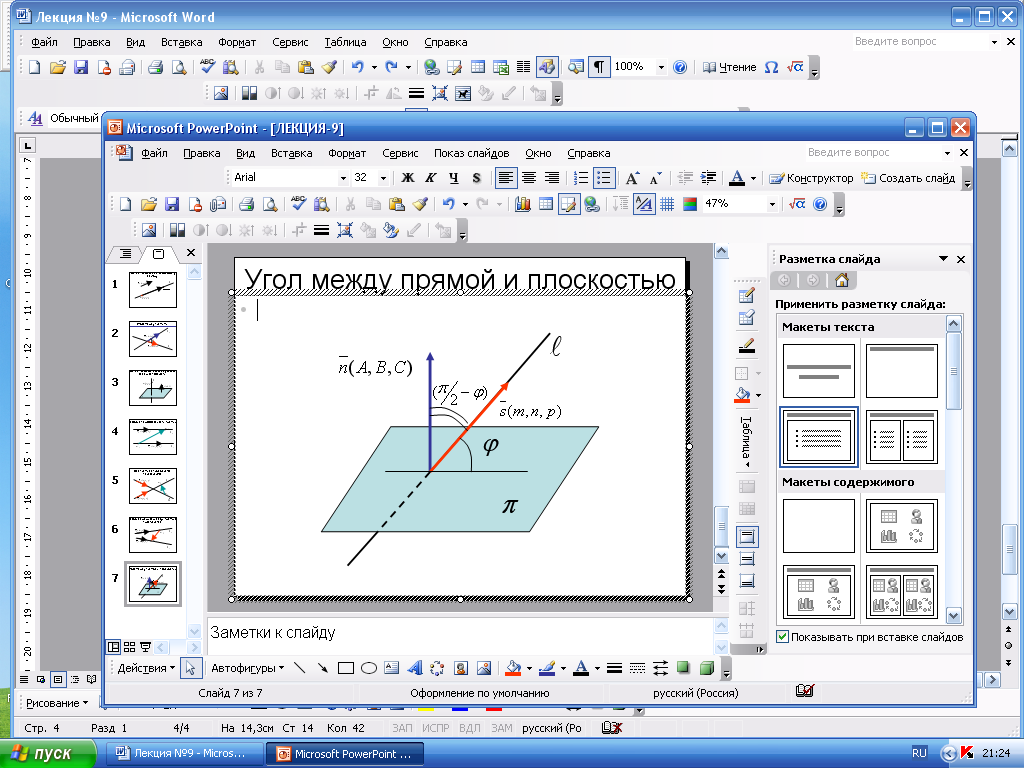
через
угол между прямой
и плоскостью
.
Тогда угол между нормалью к плоскости
вектором
и направляющим вектором прямой
будет равен
.
Тогда
sin=cos
.
Так как угол
,
то синус острого угла между прямой
и плоскостью
можно найти по формуле:
Условие
параллельности прямой
и плоскости
Е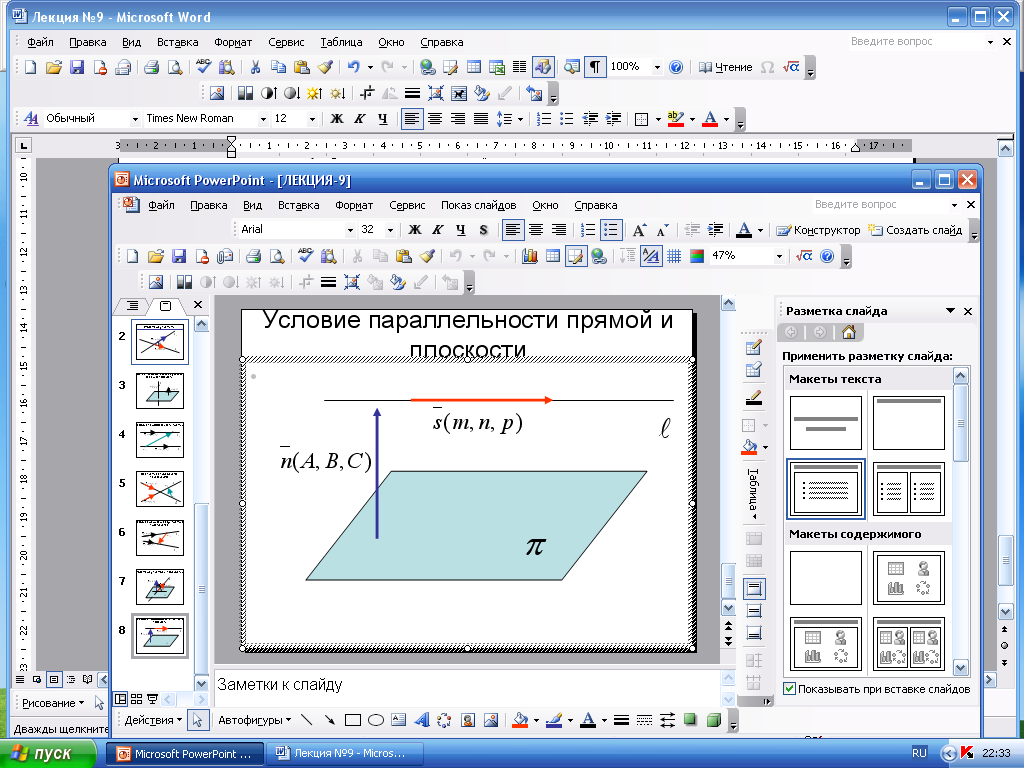
прямая
параллельна плоскости
,
то векторы
и
перпендикулярны, т.е. их скалярное
произведение равно 0.
,
т.е. в координатной форме: Am+Bn+Cp=0.
Условие
перпендикулярности прямой
и плоскости
Е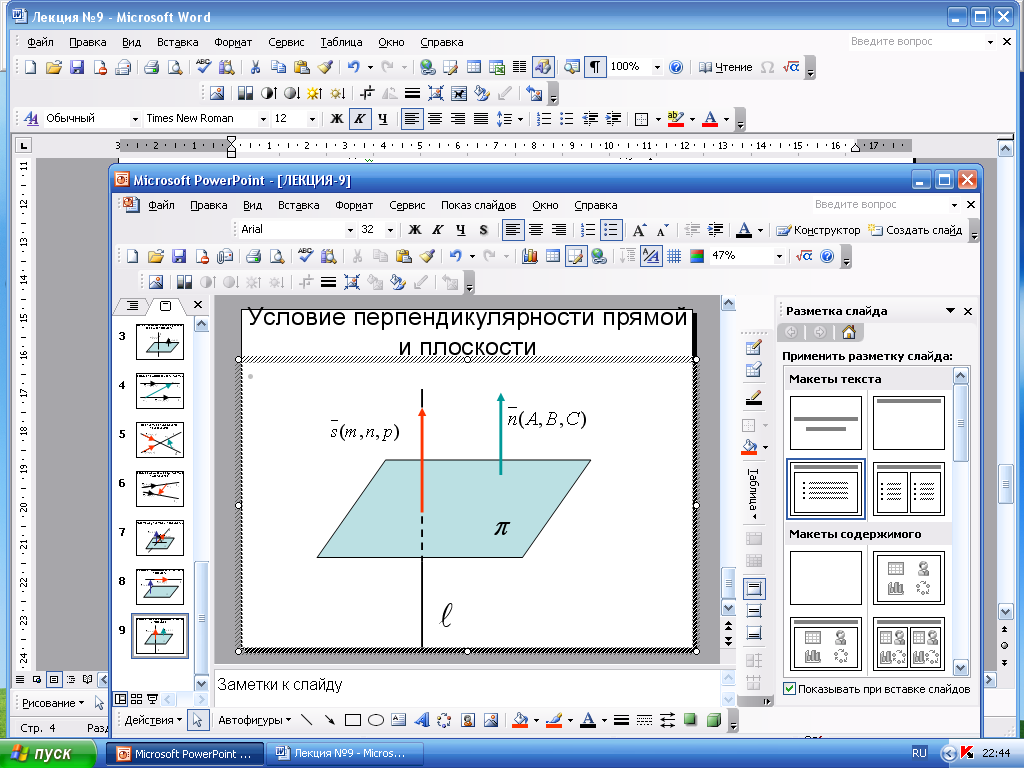
прямая
перпендикулярна
плоскости
,
то векторы
и
параллельны, т.е. должно быть выполнено
равенство:
Пересечение прямой и плоскости
Пусть
плоскость
задана своим общим уравнением:
Ax+By+Cz+D=0,
а прямая
в каноническом виде:
.
Для решения этой задачи проще всего:
прямую представить в параметрическом
виде:
где
Подставляя
выражения для x,y
и z
в уравнение плоскости:,
если:
-
данное
уравнение имеет единственное решение,
то прямая и плоскость пересекаются и
для нахождения точки пересечения,
необходимо найденное значение параметра
t
подставить в параметрическое уравнение
прямой -
если
уравнение решения не имеет, то прямая
параллельна плоскости -
если
решений множество, т.е. уравнение верно
при любом t,
то прямая принадлежит плоскости.
Кривые второго порядка
Алгебраическое
уравнение второго порядка на плоскости
описывает кривую второго порядка,
другими словами, любое уравнение вида
определяет либо одну из кривых: эллипс,
гипербола, парабола; либо распадается
на две прямые, ибо точек, удовлетворяющих
данному уравнению на плоскости нет.
Эллипс

уравнение эллипса, с центром в начале
координат:
Полуосями
этого эллипса являются по оси ОХ- отрезок
а, и по оси ОУ- отрезок b.
Таким образом, эллипс имеет две оси
симметрии: ось ОХ и ось ОУ. Четыре вершины:
точки с координатами (-а;0); (а;0); (0;-b);
(0;b).
Если величина а
b,
то .
На большей оси в точках с координатами
и (с,
0) находятся фокусы эллипса. Эксцентриситетом
эллипса называется
,т.е. отношение половины расстояния
между фокусами к большей полуоси. Для
эллипса
Характеристическое
свойство эллипса:
Эллипсом называется геометрическое
место точек, сумма расстояний от каждой
из которых до двух данных точек той же
плоскости, называемых фокусами, постоянна
и равна удвоенной большей полуоси.
-каноническое
уравнение эллипса,
центр
симметрии которого находится в точке
Q(,
полуоси
эллипса: по ОХ равна a,
по оси ОУ равна b.
Фокусы
находятся в точках:
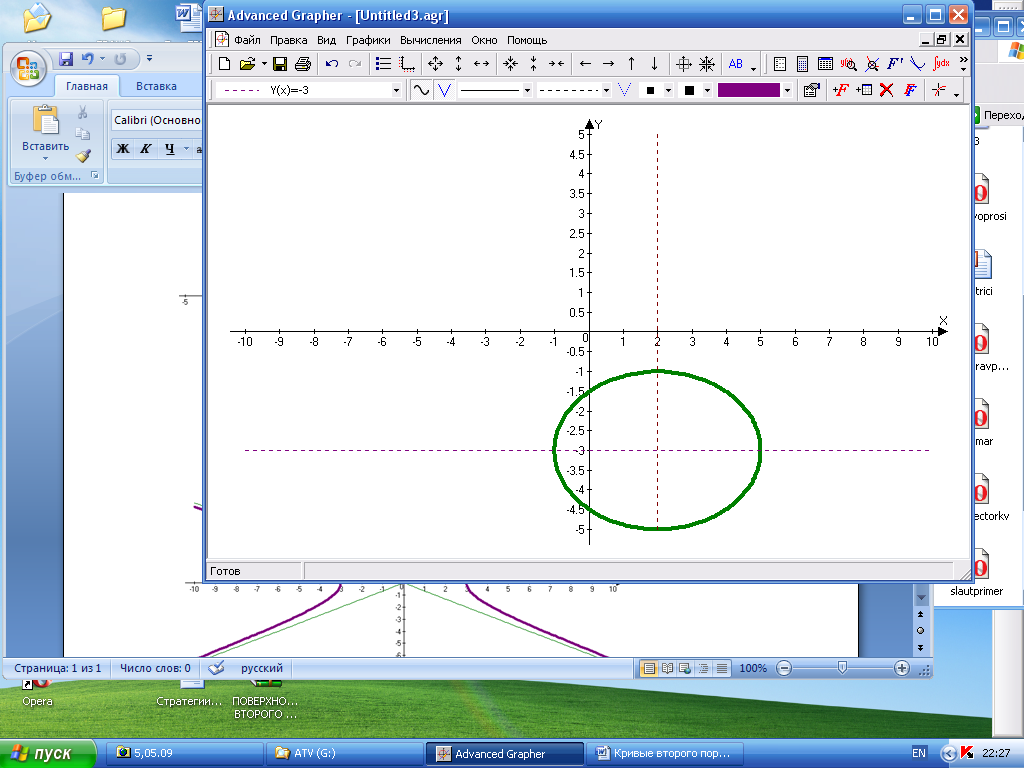
Пример: Построить
эллипс, каноническое уравнение которого:
,найти его фокусы и эксцентриситет.
Решение:
Центром симметрии эллипса является
точка Q(2;
-3), полуоси эллипса: а=3; b=2;
;
фокусы эллипса находятся в точках:
.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
- #
Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0 l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; —k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
-23 — 431 + (-23)·43
=
-631 — 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0 l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t — 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x — 23
=
y4
=
z — 35
и —
x — 22
= 1 — 3y =
3z — 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
—x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
Вы уже знакомы с понятиями угла между прямыми и угла
между векторами. А также знаете, что такое двугранный угол и угол между прямой
и плоскостью.
Сегодня мы научимся вычислять углы между прямыми, а
также между прямой и плоскостью.
Но для начала введём понятие направляющего вектора.
Определение:
Ненулевой вектор называется направляющим
вектором прямой а, если он лежит либо на прямой а, либо
на прямой, параллельной прямой а.
Понятно, что таких векторов бесконечно много и все
они коллинеарны.
Задача:
найти угол между прямыми, если известны координаты направляющих векторов этих
прямых.
Будем работать с прямыми а и b.
Для прямой a направляющим является
вектор p, а для прямой b
— вектор q.
Итак, возможны два случая.
Если угол между
направляющими векторами острый, то он равен углу между прямыми .
И если угол между
направляющими векторами тупой, то угол между
прямыми равен 180о – .
Так как в первом случае косинус угла между прямыми
равен косинусу угла между направляющими векторами, то мы можем вычислить его по
известной формуле косинуса угла между векторами.
Ну, а во втором случае записан косинус угла смежного
с углом .
Косинусы смежных углов противоположны по знаку, поэтому мы получим выражение
противоположное тому, которое было получено в первом случае.
Угол между прямыми всегда меньше либо равен 90о,
поэтому его косинус соответственно будет являться числом неотрицательным. Тогда
оба случая можно объединить в один и записать, что косинус угла между прямыми
равен частному модуля скалярного произведения направляющих векторов и
произведения их длин.
А сейчас найдём угол между прямой и плоскостью, если
известны координаты направляющего вектора к прямой и координаты ненулевого
вектора, перпендикулярного к плоскости.
Вам уже известно, что углом между прямой и
плоскостью является угол между прямой и её проекцией на эту плоскость.
Обозначим этот угол за .
А угол между направляющим вектором и вектором, перпендикулярным к плоскости
обозначим за .
Эти углы в сумме дают 90о (то есть углы и
являются
дополнительными). А нам известно, что синус угла равен косинусу дополнительного
угла. Это означает, что .
Ну, а между
векторами и
мы
без труда найдём по уже известной формуле:
Но ведь возможен и случай, когда угол между
векторами и
тупой.
Тогда углы и
являются
дополнительными, то есть их сумма равна .
Отсюда можно записать, что .
Ну, а формула косинуса угла между векторами нам уже
известна.
Чтобы объединить две полученных формулы в одну,
можно вспомнить, что синус угла от нуля до 180о является числом
неотрицательным. Тогда можно записать, что
Таким образом, мы получили формулы косинуса угла
между прямыми и синуса угла между прямой и плоскостью. Причём правые части эти
формул абсолютно совпадают.
Отличие лишь в том, что две прямые задают
направляющие векторы.
А прямую и плоскость — направляющий вектор прямой и
вектор, перпендикулярный к плоскости.
Такой вектор называют нормальным вектором к
плоскости.
Решим несколько задач.
Задача:
прямоугольный
параллелепипед, где . Найти
и
.
Решение:
ранее в таких случаях мы пытались по рисунку находить величины углов.
Но теперь мы владеем формулой косинуса угла между
прямыми.
Только для этого необходимо знать координаты
направляющих векторов прямых. В данном случае, для прямой направляющим
может является вектор ,
а для прямой
—
вектор .
Для удобства изобразим прямоугольную систему
координат так, чтобы точка совпадала
с точкой начала координат. Взяв длину рёбер и
за
единичные отрезки, можно утверждать, что длина отрезка равна
2.
Тогда не трудно определить координаты точек ,
,
и
.
Точка .
Точка .
Точка .
А точка .
Теперь не трудно найти координаты векторов и
как
разности соответствующих координат конца и начала вектора.
Получаем, что вектор .
А вектор .
Теперь можем воспользоваться формулой косинуса угла
между прямыми. Подставим координаты направляющих векторов.
А теперь, пользуясь фрагментом из таблицы Брадиса,
найдём величину данного угла, помня о том, что поправка для косинуса имеет знак
минус:
Итак, угол между прямыми .
Теперь найдём угол между прямыми и
.
В качестве направляющих векторов для данных прямых
удобно взять векторы и
.
Найдём координаты точек ,
и
.
Точка А имеет координаты .
Точка .
А точка .
Тогда вектор .
А вектор .
Подставим значения координат направляющих векторов в
формулу косинуса угла между прямыми.
В ходе вычислений получаем
Вычислив примерное значение этой дроби, можем
воспользоваться таблицей Брадиса:
Так получаем, что угол между прямыми .
Вот так по координатам направляющих векторов находят
величину угла между прямыми.
Задача:
тетраэдр.
.
,
а .
Вычислить синус угла между прямой, проходящей через
середины рёбер и
,
и плоскостью: а) ;
б) ;
в) .
Решение:
По условию рёбра ,
и
взаимно
перпендикулярны. Поэтому можно изобразить прямоугольную систему координат так,
чтобы точка совпадала
с точкой начала координат.
Тогда зная длины рёбер ,
и
не
трудно отметить единичные отрезки и определить координаты всех вершин.
Мы с вами будем находить синус угла между прямой и
каждой из данных плоскостей.
Сначала разберёмся с прямой. Она проходит через
середины рёбер и
,
пусть это будут точки и
.
И для вычисления синуса угла нужно знать координаты направляющего вектора. В
качестве направляющего вектора можно взять вектор .
Координаты точки найдём
как координаты середины отрезка .
Каждая из них равна полусумме соответствующих координат точек и
.
Так получаем,
,
.
Аналогично найдём координаты точки ,
как полусумму соответствующих координат точек и
.
Получаем ,
.
Теперь можем найти координаты вектора как
разности соответствующих координат.
Получаем, что направляющий вектор данной прямой
имеет координаты .
Также для вычисления синуса угла между прямой и
плоскостью необходимо знать координаты нормального вектора к плоскости, то есть
перпендикулярного к ней.
Задача:
Доказать, что угол между скрещивающимися прямыми, одна из которых содержит
диагональ куба, а другая — диагональ грани куба, равен .
Решение:
изобразим прямоугольную координатную плоскость так, чтобы координатные оси
совпадали с рёбрами куба.
Обозначим буквами вершины куба, через которые проходят
данные скрещивающиеся прямые. Найдём угол между прямыми .
Пусть длина единичных отрезков на осях равна длине
ребра куба.
Тогда в такой системе координат нетрудно найти
координаты точек О, О1, О2 и О3.
А теперь найдём координаты векторов ОО1 и
О2О3, которые являются направляющими для данных прямых.
Вектор .
А вектор .
Найдём косинус угла между данными прямыми, подставив
в формулу координаты направляющих векторов.
В ходе вычислений получаем, что
А значит, угол между прямыми .
Что и требовалось доказать.
Итоги:
На этом уроке мы получили формулу вычисления
косинуса угла между прямыми по координатам их направляющих векторов. А также
формулу вычисления синуса угла между прямой и плоскостью по координатам
направляющего вектора данной прямой и нормального вектора данной плоскости.