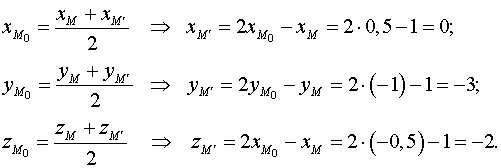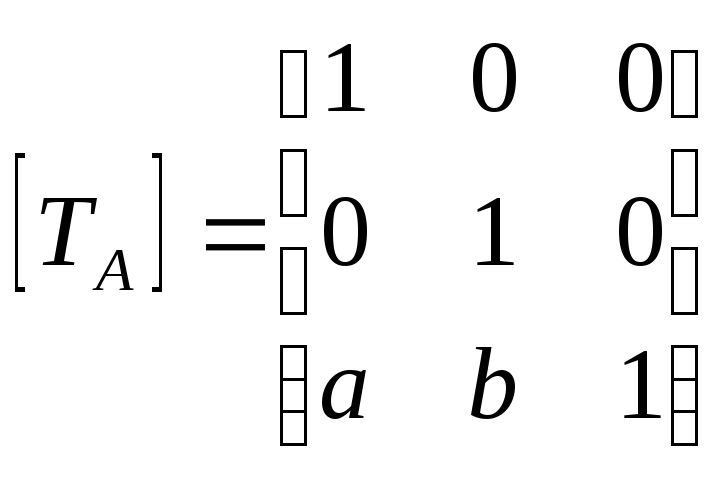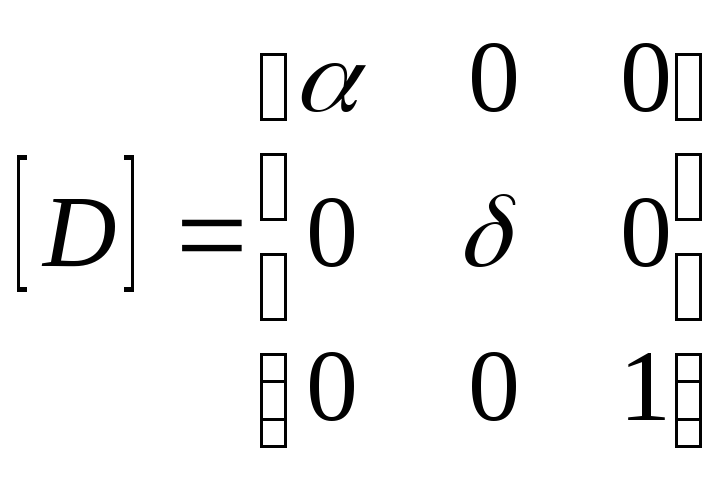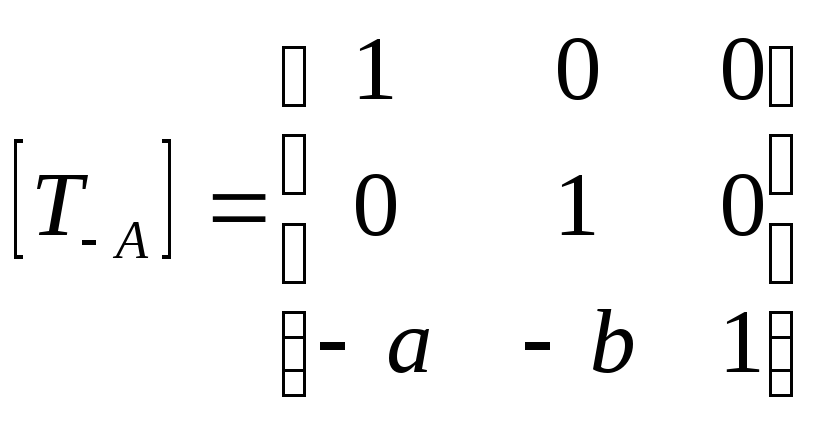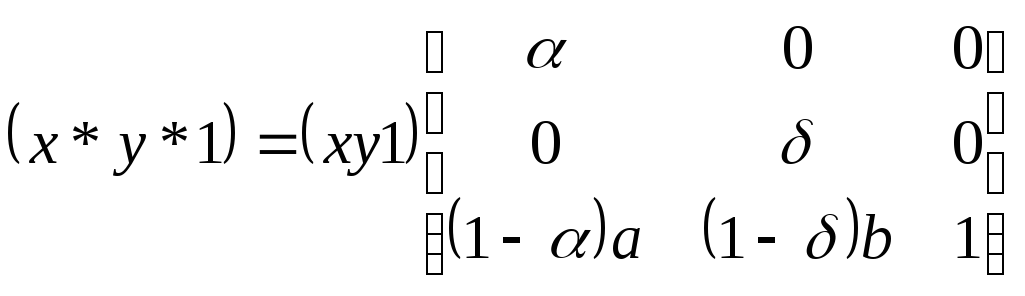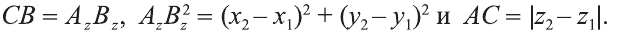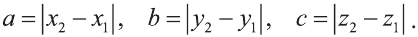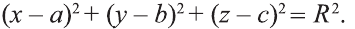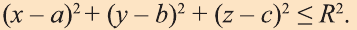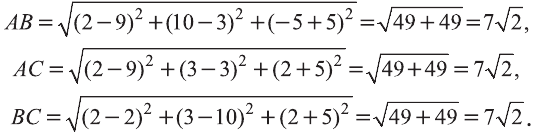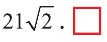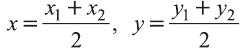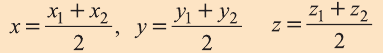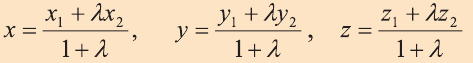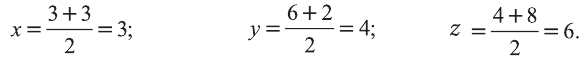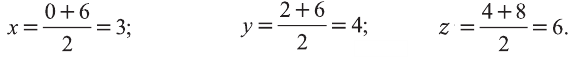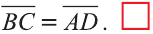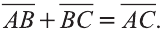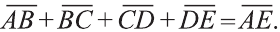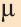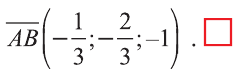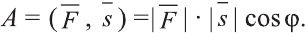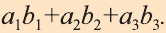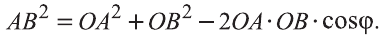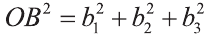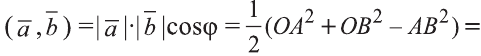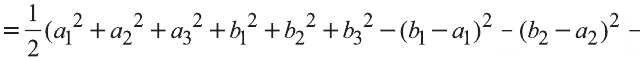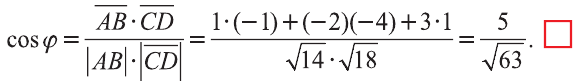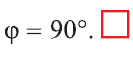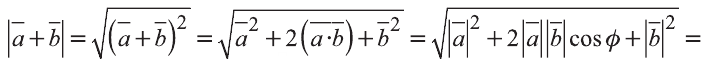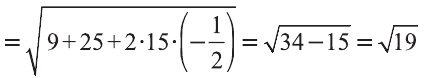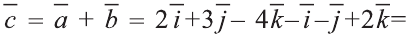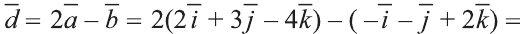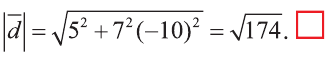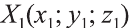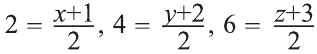Как найти симметричные точки относительно координатных плоскостей

Симметрия относительно плоскости

Постановка
задачи.
Найти координаты точки
,
симметричной точкеотносительно
плоскости.

План
решения.

1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.

.

Поэтому
уравнение прямой будет

.

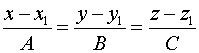
2.
Находим точку
пересечения
прямойи
плоскости(см.
задачу 13).

3.
Точка
является
серединой отрезка,
где точкаявляется
точкой симметричной точке,
поэтому

.

Задача
14.
Найти точку
,
симметричную точкеотносительно
плоскости.

Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

.

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.является
серединой отрезка,
поэтому

Т.е.
.

1. Однородные координаты плоскости.
   Аффинные преобразования на плоскости.

Пусть М
— произвольная точка плоскости с
координатами х
и у,
вычисленными относительно заданной
прямолинейной координатной системы.
Однородными координатами этой точки
называется любая тройка одновременно
неравных нулю чисел х₁,
х₂,
х₃,
связанных с заданными числами х и у
следующими соотношениями:

При решении задач
компьютерной графики однородные
координаты обычно вводятся так:
произвольной точке М
(х,
у)
плоскости ставится в соответствие точка
Мэ
(х,
у,
1) в пространстве (рис. 8).

Рис. 8

Заметим, что
произвольная точка на прямой, соединяющей
начало координат, точку 0(0, 0, 0), с точкой
Мэ
(х,
у,
1), может быть задана тройкой чисел вида
(hx,
hy,
h).

Будем считать, что
h 
0.

Вектор с координатами
hx,
hy, является направляющим вектором
прямой, соединяющей точки 0 (0, 0, 0) и Мэ
(х,
у,
1). Эта прямая пересекает плоскость z
= 1 в точке (х, у, 1), которая однозначно
определяет точку (х, у) координатной
плоскости ху.

Тем самым между
произвольной точкой с координатами (х,
у) и множеством троек чисел вида

(hx,
hy,
h),
h

0,

устанавливается
(взаимно однозначное) соответствие,
позволяющее считать числа hx,
hy,
h
новыми координатами этой точки.

Замечание

Широко используемые
в проективной геометрии однородные
координаты позволяют эффективно
описывать так называемые несобственные
элементы (по существу те, которыми
проективная плоскость отличается от
привычной нам евклидовой плоскости).
Более подробно о новых возможностях,
предоставляемых введенными однородными
координатами, говорится в четвертом
разделе этой главы.

В проективной
геометрии для однородных координат,
принято следующее обозначение:

х : у : 1 , или, более
обще, x₁
: х₂
: х₃

(напомним, что
здесь непременно требуется, чтобы числа
х₁,
х₂,
х₃
одновременно, в нуль не обращались).

Применение
однородных координат оказывается
удобным уже при решении простейших
задач.

Рассмотрим,
например, вопросы, связанные с изменением
масштаба. Если устройство отображения
работает только с целыми числами (или
если необходимо работать только с целыми
числами), то для произвольного значения
h
(например, h
= 1) точку с однородными координатами

(0.5 0.1 2.5)

представить нельзя.
Однако при разумном выборе h
можно добиться того, чтобы координаты
этой точки были целыми числами. В
частности, при h = 10 для рассматриваемого
примера имеем

(5, 1, 25).

Рассмотрим другой
случай. Чтобы результаты преобразования
не приводили к арифметическому
переполнению, для точки с координатами
(80000 40000 1000) можно взять, например, h=0,001.
В результате получим (80 40 1).

Приведенные примеры
показывают полезность использования
однородных координат при проведении
расчетов. Однако основной целью введения
однородных координат в компьютерной
графике является их несомненное удобство
в применении к геометрическим
преобразованиям.

При помощи троек
однородных координат и матриц третьего
порядка можно описать любое аффинное
преобразование плоскости.

В самом деле, считая
h
= 1, сравним две записи: помеченную
символом * и нижеследующую, матричную:

Нетрудно заметить,
что после перемножения выражений,
стоящих в правой части последнего
соотношения, мы получим обе формулы (*)
и верное числовое равенство 1=1.

Тем самым сравниваемые
записи можно считать равносильными.

Замечание

Иногда в литературе
используется другая запись – запись
по столбцам:

Такая запись
эквивалентна приведенной выше записи
по строкам (и получается из нее
транспонированием).

Элементы произвольной
матрицы аффинного преобразования не
несут в себе явно выраженного
геометрического смысла. Поэтому чтобы
реализовать то или иное отображение,
то есть найти элементы соответствующей
матрицы по заданному геометрическому
описанию, необходимы специальные приемы.
Обычно построение этой матрицы в
соответствии со сложностью рассматриваемой
задачи и с описанными выше частными
случаями разбивают на несколько этапов.

На каждом этапе
ищется матрица, соответствующая тому
или иному из выделенных выше случаев
А, Б, В или Г, обладающих хорошо выраженными
геометрическими свойствами.

Выпишем соответствующие
матрицы третьего порядка.

А. Матрица вращения,
(rotation)

Б. Матрица растяжения
(сжатия) (dilatation)
•

В. Матрица отражения
(reflection)

Г. Матрица переноса
(translation)

Рассмотрим примеры
аффинных преобразований плоскости.

Пример 1.

Построить матрицу
поворота вокруг точки А (а, b)
на угол 
(рис. 9).

Рис. 9.

1-й шаг.
Перенос на вектор – А (-а, -b)
для совмещения центра поворота с началом
координат;

матрица
соответствующего преобразования.

2-й шаг.
Поворот на угол 

матрица
соответствующего преобразования.

3-й шаг.
Перенос на вектор А(а,b)
для возвращения центра поворота в
прежнее положение;

матрица
соответствующего преобразования.

Перемножим матрицы
в том же порядке, как они выписаны:

В
результате получим, что искомое
преобразование (в матричной записи)
будет выглядеть следующим образом:

Элементы полученной
матрицы (особенно в последней строке)
не так легко запомнить. В то же время
каждая из трех перемножаемых матриц по
геометрическому описанию соответствующего
отображения легко строится.

Пример 3

Построить матрицу
растяжения с коэффициентами растяжения

вдоль оси абсцисс и 
вдоль оси ординат и с центром в точке
А(а, b).

1-й шаг.
Перенос на вектор -А(-а, -b) для совмещения
центра растяжения с началом координат;

матрица
соответствующего преобразования.

2-й шаг.
Растяжение вдоль координатных осей с
коэффициентами 
и 
соответственно; матрица преобразования
имеет вид

3-й шаг.
Перенос на вектор А(а, b) для возвращения
центра растяжения в прежнее положение;
матрица соответствующего преобразования
–

Перемножив .матрицы
в том же порядке

получим окончательно

Замечание

Рассуждая подобным
образом, то есть разбивая предложенное
преобразование на этапы, поддерживаемые
матрицами [R],[D],[M],[T],
можно построить
матрицу любого аффинного преобразования
по его геометрическому описанию.

Пусть М
— произвольная точка плоскости с
координатами х
и у,
вычисленными относительно заданной
прямолинейной координатной системы.
Однородными координатами этой точки
называется любая тройка одновременно
неравных нулю чисел х₁,
х₂,
х₃,
связанных с заданными числами х и у
следующими соотношениями:

При решении задач
компьютерной графики однородные
координаты обычно вводятся так:
произвольной точке М
(х,
у)
плоскости ставится в соответствие точка
Мэ
(х,
у,
1) в пространстве (рис. 8).

Рис. 8

Заметим, что
произвольная точка на прямой, соединяющей
начало координат, точку 0(0, 0, 0), с точкой
Мэ
(х,
у,
1), может быть задана тройкой чисел вида
(hx,
hy,
h).

Будем считать, что
h 
0.

Вектор с координатами
hx,
hy, является направляющим вектором
прямой, соединяющей точки 0 (0, 0, 0) и Мэ
(х,
у,
1). Эта прямая пересекает плоскость z
= 1 в точке (х, у, 1), которая однозначно
определяет точку (х, у) координатной
плоскости ху.

Тем самым между
произвольной точкой с координатами (х,
у) и множеством троек чисел вида

(hx,
hy,
h),
h

0,

устанавливается
(взаимно однозначное) соответствие,
позволяющее считать числа hx,
hy,
h
новыми координатами этой точки.

Замечание

Широко используемые
в проективной геометрии однородные
координаты позволяют эффективно
описывать так называемые несобственные
элементы (по существу те, которыми
проективная плоскость отличается от
привычной нам евклидовой плоскости).
Более подробно о новых возможностях,
предоставляемых введенными однородными
координатами, говорится в четвертом
разделе этой главы.

В проективной
геометрии для однородных координат,
принято следующее обозначение:

х : у : 1 , или, более
обще, x₁
: х₂
: х₃

(напомним, что
здесь непременно требуется, чтобы числа
х₁,
х₂,
х₃
одновременно, в нуль не обращались).

Применение
однородных координат оказывается
удобным уже при решении простейших
задач.

Рассмотрим,
например, вопросы, связанные с изменением
масштаба. Если устройство отображения
работает только с целыми числами (или
если необходимо работать только с целыми
числами), то для произвольного значения
h
(например, h
= 1) точку с однородными координатами

(0.5 0.1 2.5)

представить нельзя.
Однако при разумном выборе h
можно добиться того, чтобы координаты
этой точки были целыми числами. В
частности, при h = 10 для рассматриваемого
примера имеем

(5, 1, 25).

Рассмотрим другой
случай. Чтобы результаты преобразования
не приводили к арифметическому
переполнению, для точки с координатами
(80000 40000 1000) можно взять, например, h=0,001.
В результате получим (80 40 1).

Приведенные примеры
показывают полезность использования
однородных координат при проведении
расчетов. Однако основной целью введения
однородных координат в компьютерной
графике является их несомненное удобство
в применении к геометрическим
преобразованиям.

При помощи троек
однородных координат и матриц третьего
порядка можно описать любое аффинное
преобразование плоскости.

В самом деле, считая
h
= 1, сравним две записи: помеченную
символом * и нижеследующую, матричную:

Нетрудно заметить,
что после перемножения выражений,
стоящих в правой части последнего
соотношения, мы получим обе формулы (*)
и верное числовое равенство 1=1.

Тем самым сравниваемые
записи можно считать равносильными.

Замечание

Иногда в литературе
используется другая запись – запись
по столбцам:

Такая запись
эквивалентна приведенной выше записи
по строкам (и получается из нее
транспонированием).

Элементы произвольной
матрицы аффинного преобразования не
несут в себе явно выраженного
геометрического смысла. Поэтому чтобы
реализовать то или иное отображение,
то есть найти элементы соответствующей
матрицы по заданному геометрическому
описанию, необходимы специальные приемы.
Обычно построение этой матрицы в
соответствии со сложностью рассматриваемой
задачи и с описанными выше частными
случаями разбивают на несколько этапов.

На каждом этапе
ищется матрица, соответствующая тому
или иному из выделенных выше случаев
А, Б, В или Г, обладающих хорошо выраженными
геометрическими свойствами.

Выпишем соответствующие
матрицы третьего порядка.

А. Матрица вращения,
(rotation)

Б. Матрица растяжения
(сжатия) (dilatation)
•

В. Матрица отражения
(reflection)

Г. Матрица переноса
(translation)

Рассмотрим примеры
аффинных преобразований плоскости.

Пример 1.

Построить матрицу
поворота вокруг точки А (а, b)
на угол 
(рис. 9).

Рис. 9.

1-й шаг.
Перенос на вектор – А (-а, -b)
для совмещения центра поворота с началом
координат;

матрица
соответствующего преобразования.

2-й шаг.
Поворот на угол 

матрица
соответствующего преобразования.

3-й шаг.
Перенос на вектор А(а,b)
для возвращения центра поворота в
прежнее положение;

матрица
соответствующего преобразования.

Перемножим матрицы
в том же порядке, как они выписаны:

В
результате получим, что искомое
преобразование (в матричной записи)
будет выглядеть следующим образом:

Элементы полученной
матрицы (особенно в последней строке)
не так легко запомнить. В то же время
каждая из трех перемножаемых матриц по
геометрическому описанию соответствующего
отображения легко строится.

Пример 3

Построить матрицу
растяжения с коэффициентами растяжения

вдоль оси абсцисс и 
вдоль оси ординат и с центром в точке
А(а, b).

1-й шаг.
Перенос на вектор -А(-а, -b) для совмещения
центра растяжения с началом координат;

матрица
соответствующего преобразования.

2-й шаг.
Растяжение вдоль координатных осей с
коэффициентами 
и 
соответственно; матрица преобразования
имеет вид

3-й шаг.
Перенос на вектор А(а, b) для возвращения
центра растяжения в прежнее положение;
матрица соответствующего преобразования
–

Перемножив .матрицы
в том же порядке

получим окончательно

Замечание

Рассуждая подобным
образом, то есть разбивая предложенное
преобразование на этапы, поддерживаемые
матрицами [R],[D],[M],[T],
можно построить
матрицу любого аффинного преобразования
по его геометрическому описанию.

Сдвиг
реализуется сложением, а масштабирование
и поворот — умножением.

Преобразование
масштабирования
(дилатация) относительно начала координат
имеет вид:

или
в матричной форме:

где
Dx,
Dy
– коэффициенты
масштабирования по осям, а

—
матрица  масштабирования.

При
D
> 1-происходит расширение, при 0<=D<1-
сжатие

Преобразование
поворота
относительно начала координат имеет
вид:

или
в матричной форме:

где
φ – угол поворота, а

—
матрица поворота.

Замечание:
Столбцы
и строки матрицы поворота представляют
собой взаимно ортогональные единичные
векторы. В самом деле квадраты длин
векторов-строк равны единице:

cosφ·cosφ+sinφ·sinφ
= 1 и (-sinφ)
·(-sinφ)+cosφ·cosφ
= 1,

а
скалярное произведение векторов-строк
есть

cosφ·(-sinφ)
+ sinφ·cosφ=
0.

Так
как скалярное произведение векторов A
·B
= |A|
·|B|
·cosψ, где |A|
— длина вектора A,
|B|
— длина вектора B,
а ψ – наименьший положительный угол
между ними, то из равенства 0 скалярного
произведения двух векторов-строк длины
1 следует, что угол между ними равен 90^°.

Условие

Решение

Написать комментарий

Геометрия, 11 класс

Урок №5. Метод преобразований решения задач

Перечень вопросов, рассматриваемых в теме:

• симметрия относительно произвольной плоскости;
• понятие «метод движений» в пространстве.

Глоссарий по теме

Метод геометрических преобразований

Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.

Метод параллельного переноса

Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.

Метод симметрии

Применение симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой точки/оси/плоскости.

Метод поворота

Идея метода поворота состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл.: учеб. для общеобразоват. учреждений /– М.: Дрофа, 2009. – 235,: ил., ISBN 978–5–358–05346–5, сс. 178-196. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. учреждений– М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Метод геометрических преобразований

Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.

1.1. Метод параллельного переноса.

Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.

Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных.

1.2. Метод симметрии.

Применение осевой симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в некоторых случаях симметрия непосредственно даёт искомые точки.

Метод симметрии заключается в следующем. Предполагают задачу решённой и одну из данных точек (прямую или окружность) отражают в какой-нибудь известной оси; иногда эта ось проходит через известную точку. Тогда полученную симметричную точку (прямую или окружность) подчиняют тем же условиям, которым должна была удовлетворять заменённая точка (прямая или окружность). После этого получится новая задача, которую решают способами, уже нам известными. Обыкновенно, с решением этой новой задачи предложенная задача уже будет решена сама собой, и только в редких случаях придётся ещё переходить к первоначальным условиям задачи. Таким образом, метод симметрии приводит решение предложенной задачи к решению новой задачи.

1.3. Метод поворота.

Поворотом также пользуются как методом решения геометрических задач на построение. Идея метода вращения состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

2. Решение задач методом преобразований

2.1. Симметрия относительно произвольной плоскости

Постановка задачи. Найти координаты точки , симметричной точке , относительно плоскости Ax + By + Cz + D = 0.

План решения.

1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку . Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е. .

Поэтому уравнение прямой будет:

2. Находим точку пересечения прямой и плоскости Ax + By + Cz + D = 0.

Для этого обозначим и выразим x, y, z:

.

Подставим x, y, z в уравнение плоскости:

найдем значение t.

Затем найдем x, y, z. Найденные координаты будут являться координатами точки .

3. Точка является серединой отрезка , где точка является точкой симметричной точке , поэтому

, , .

Задача 1. Найти точку M’, симметричную точке M относительно плоскости.

M(1, 1, 1), x + 4y + 3z + 5 = 0.

Решение:

Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:

.

Найдем точку пересечения прямой и плоскости.

,

,

(1 + t) + 4(1 + 4t) + 3(1 + 3t) + 5 = 0,

t = -0,5.

Откуда – точка пересечения прямой и плоскости. является серединой отрезка MM’, поэтому

,

,

,

2.2. Задача 2

Даны плоскость α: x + 2y – z – 2 = 0 и две точки А(1, -2, -3) и В (-1, -1, -2). Найдите на этой плоскости точку С такую, чтобы ломаная АСВ имела наименьшую длину.

Решение:

Данная плоскость пересекает оси координат в точках

M (2, 0, 0) (ось OX)

N (0, 1, 0) (ось OY)

K (0, 0, 2) (ось OZ)

Две заданные точки лежат по одну сторону от данной плоскости.

Если бы две точки лежали по разные стороны от плоскости α, то очевидно, искомой точкой С была бы точка пересечения отрезка, концами которого являются данные точки, с плоскостью α, а ломаная выродилась бы в отрезок.

Сведем нашу задачу к описанной ситуации.

Для этого найдем точку, симметричную любой из заданных относительно данной плоскости α.

Например, точке А.

Используя решение задачи 1, получим следующую последовательность действий.

Уравнение прямой, которая проходит через точку А перпендикулярно заданной плоскости будет:

.

Найдем точку пересечения полученной прямой и плоскости α.

.

.

(1 + t) + 2(2t – 2) — (-t– 2) – 2 = 0

t = 0,5

Откуда точка пересечения прямой, перпендикулярной плоскости α и проходящей через точку А, с плоскость α . Точка пересечения прямой и плоскости. является серединой отрезка АА’, поэтому

,

,

,

A'(2; 0; -4)

Теперь найдем точку пересечения отрезка A’B с плоскостью α.

Прямая A’B имеет направляющий вектор .

Уравнение прямой A’B:

.

Найдем точку пересечения полученной прямой и плоскости α.

.

.

3t-1+2(t-2)-(-2t-2)-2=0

7t-5=0

.

Таким образом, координаты искомой точки .

Ответ: .

Примеры и разбор решения заданий тренировочного модуля

1. Напишите уравнение образа плоскости 2x + 5y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Решение:

Найдем координаты двух точек плоскости 2x + 5y – z – 5 = 0, лежащих в плоскости Oxz. Для этого найдем точки плоскости, принадлежащие осям координат.

OX: z = y = 0, x = 2,5 A(2,5; 0; 0)

OZ: x = y = 0, z = -5 B(0; 0; -5).

Эти точки принадлежат и образу плоскости 2x + 3y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Теперь найдем точку данной плоскости, принадлежащую оси ординат.

OY: z = x = 0, y = 2,5 С(0; 1; 0).

Точка, симметричная точке С относительно плоскости Oxz, имеет координаты С'(0; -1; 0).

Теперь напишем уравнение плоскости через три полученные точки.

Оно имеет вид:

— 5x + 12.5y + 2.5z + 12.5 = 0

2x — 5y — z — 5 = 0

Ответ: 2x — 5y — z — 5 = 0

§ 4.Симметрия относительно плоскости

4.1.Определение симметрии относительно плоскости

Определение. Точка m′ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ′ перпендикулярен этой плоскости и делится ею пополам. Любая точка плоскости α считается симметричной самой себе относительно этой плоскости (рис. 19).

Из определения следует, что если точка M′ симметрична точке M относительно плоскости α, то точка М симметрична точке М′ относительно той же плоскости α.

Зададим теперь следующее отображение пространства на себя. Каждой точке М пространства поставим в соответствие точку М′, симметричную ей относительно плоскости α. Аналогично центральной симметрии, можно доказать, что это отображение является преобразованием пространства. При этом каждая точка плоскости α отображается на себя.

Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется симметрией пространства относительно плоскости α. Плоскость α называется плоскостью симметрии.

Симметрия относительно плоскости α обозначается Sα. Если при этой симметрии точка М (фигура F) отображается на точку М′ (фигуру F′), то записывают Sα(М) = М′ (Sα(F) = F′). Это преобразование ещё называют «отражением в плоскости», или «зеркальной симметрией», или «зеркальным отражением от плоскости», проводя аналогию с «отражением в зеркале».

Из определения симметричных точек относительно плоскости α следует

Sα(M) = M′ ⇔ Sα(M′) = M.

Поэтому говорят, что точки М и М′ симметричны относительно плоскости α. С другой стороны, ранее было показано, что точка M′ отображается на свой прообраз — точку M — преобразованием, обратным данному. Значит,

Sα(M) = M′ ⇒ (M′) = M.

Получили

Таким образом, симметрия относительно плоскости есть преобразование пространства, совпадающее со своим обратным преобразованием.

Тогда для любой точки М пространства имеем

(Sα ∘ Sα)(M) = Sα(Sα (M)) = Sα(M′) = (M′) = M.

Но для тождественного преобразования E справедливо Е(М) = М. Так как точка М — любая, то преобразования Sα ∘ Sα и Е равны: Sα ∘ Sα = Е, т. е. композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование.

Если при симметрии относительно плоскости α фигура F отображается на себя (Sα(F) = F), то плоскость α называется плоскостью симметрии этой фигуры. При этом говорят, что фигура F симметрична относительно плоскости α (или плоскость α является плоскостью симметрии фигуры F).

Например, плоскость, проходящая через середины параллельных рёбер AD, ВС, B1C1 и A1D1 куба АВСDA1B1C1D1 (рис. 20), является плоскостью симметрии этого куба. Докажите это и найдите другие плоскости симметрии данного куба.

Симметрия относительно плоскости может быть задана парой соответственных (симметричных) точек А и A′ (почему?).

4.2.Симметрия относительно плоскости в координатной форме

Выведем формулы, которые позволяли бы по координатам произвольной точки М пространства находить координаты её образа — точки M′ = Sα(M).

Выберем прямоугольную систему координат Oхyz так, чтобы её координатная плоскость Оху совпадала с плоскостью симметрии α. Рассмотрим в этой системе координат произвольную точку M(x; y; z) и её образ М′(x′; y′; z′) при симметрии относительно плоскости Oxy (рис. 21).

По определению симметрии относительно плоскости имеем MM′ ⟂ (Оху), | M0M | = | M0M′ |, где M0 — точка пересечения прямой ММ′ с плоскостью Оху. Это означает, что точки М и M′ расположены в разных полупространствах относительно плоскости Oxy, одинаково удалены от неё, а прямая MM′ параллельна координатной оси Oz. Поэтому координаты этих точек связаны соотношениями

x′ = x, y′ = y, z′ = –z,

которые называются формулами npeoбразованuя симметрии относительно плоскости Oxy.

4.3.Симметрия относительно плоскости — движение пространства

Используя формулы симметрии в координатах, докажем, что симметрия относительно плоскости — движение пространства.

Пусть A(x1; y1; z1), C(x2; y2; z2) — данные точки, тогда A′(x1; y1; –z1), C′(x2; y2; –z2) — их образы при симметрии S(Oxy).

Находим:

т. е. рассматриваемая симметрия является движением, что и требовалось доказать. ▼

4.4. Свойства симметрии относительно плоскости

Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях зеркальной симметрии.

Неподвижной точкой симметрии относительно плоскости α является каждая точка плоскости α; других неподвижных точек при данной симметрии нет.

Неподвижные прямые симметрии Sα относительно плоскости α можно разделить на два вида:

—каждая прямая плоскости α; любая точка такой прямой является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на каждой из этих прямых тождественное преобразование Е;

—каждая прямая пространства, перпендикулярная плоскости α; на любой такой прямой индуцируется центральная симметрия относительно точки пересечения этой прямой с плоскостью α.

Неподвижные плоскости симметрии Sα можно разделить также на два вида:

—сама плоскость α; каждая её точка является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на этой плоскости тождественное преобразование E;

—каждая плоскость, перпендикулярная плоскости α; на любой такой плоскости индуцируется известная вам из планиметрии осевая симметрия относительнo прямой пересечения этой плоскости с плоскостью α.

Для исследования вопроса о том, меняет ли симметрия относительно плоскости ориентацию тетраэдра, выберем такую тройку единичных попарно взаимно перпендикулярных векторов , и , чтобы точки O, А и В лежали в плоскости α. Тогда при симметрии Sα тетраэдр ОАВС отобразится на такой тетраэдр ОАВC′, что ′ = – (рис. 22). Это означает, что ориентации тетраэдров ОАВС и ОАВC′ = Sα(OABC) различны, т. е. симметрия относительно плоскости меняет ориентацию тетраэдра, следовательно, является движением второго рода.

Интересно заметить, что если три плоскости α, β и γ попарно взаимно перпендикулярны, то композиция симметрий относительно этих трёх плоскостей является центральной симметрией относительно их общей точки (точки пересечения плоскостей α, β и γ), т. е. Sγ ∘ Sβ ∘ Sα = ZО, где О — общая точка этих трёх плоскостей. Попробуйте самостоятельно доказать это координатным методом.

Содержание:

Система координат в пространстве

Декартова система координат в пространстве

Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.

Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

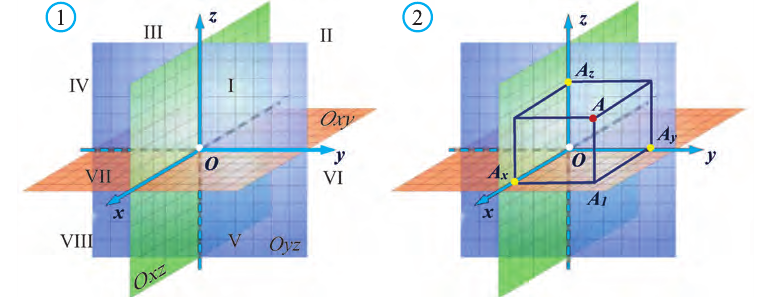
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.

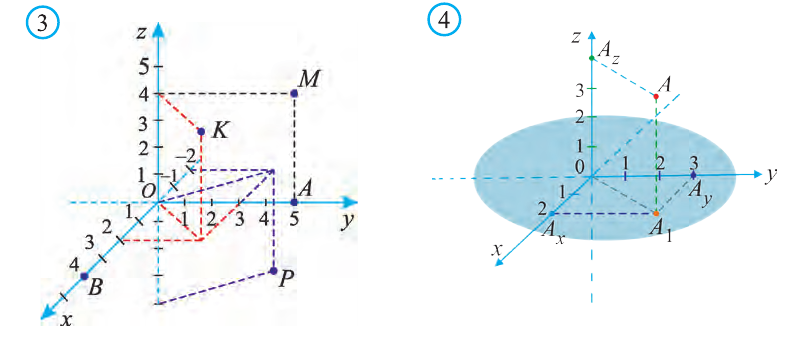
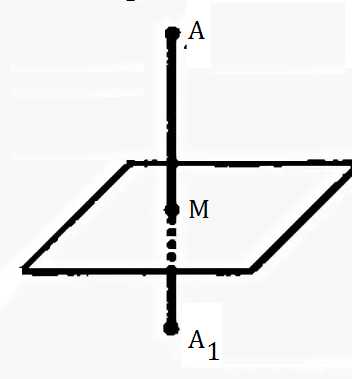
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).

Пример:

Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

Пусть заданы две точки А (х₁; у₁; z₁) и B (х₂; у₂; z₂).

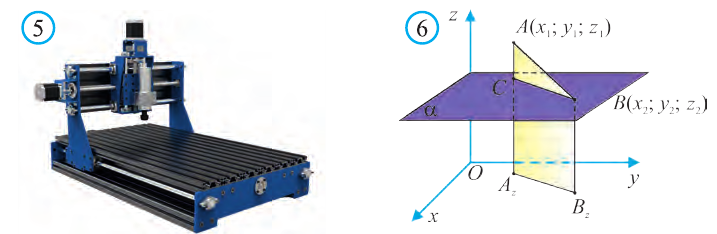
1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ² = АС² + СВ².

Однако

Поэтому

2.Пусть отрезок АВ параллелен оси Оz, тогда 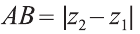и, так как

х₁= х₂ , у₁ = у₂ , мы опять приходим к вышеприведённой формуле.

Следовательно, расстояние между двумя точками А и В:

(1)

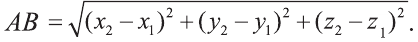
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны

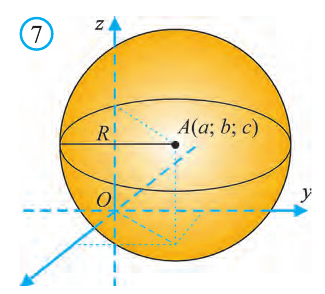
Уравнение сферы и шара

Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид:

Пример:

Найдите периметр треугольника ABC с вершинами в

точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 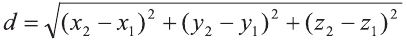расстояния между двумя точками, найдём длины сторон треугольника:

Следовательно, треугольник ABC равносторонний и его периметр .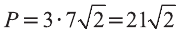

Ответ:

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).

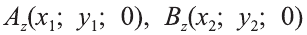
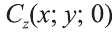
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках и . Тогда по теореме Фалеса точка С_z — середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

Аналогично, используя координаты концов A и B отрезка AB, по формулам

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

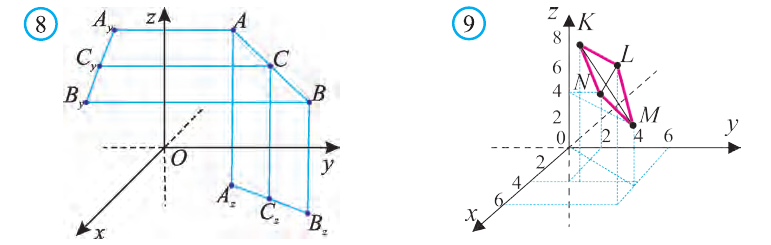
Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; — параллелограмм (рис. 9).

Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

Координаты середины отрезка NL:

Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

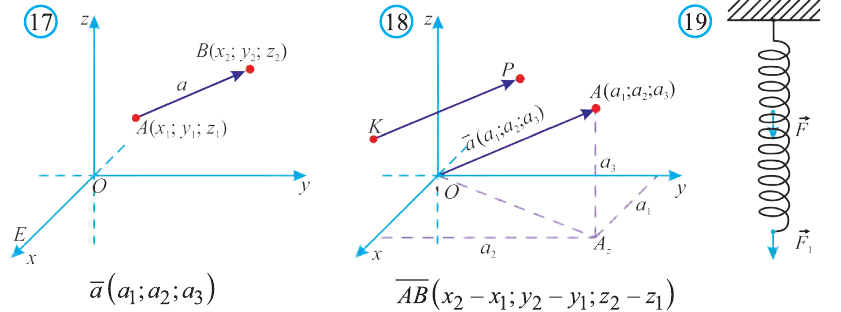
Векторы в пространстве и действия над ними

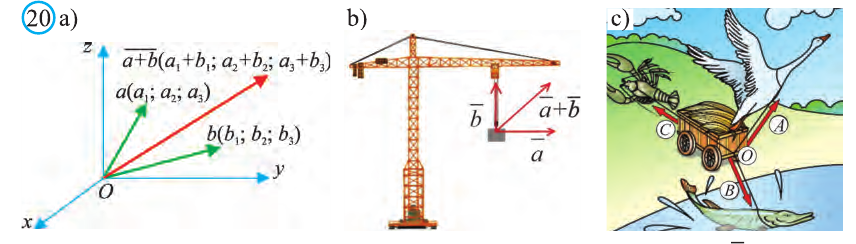
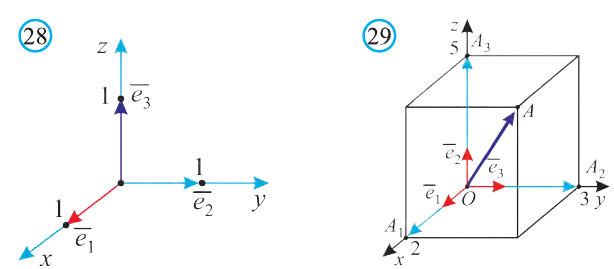
Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

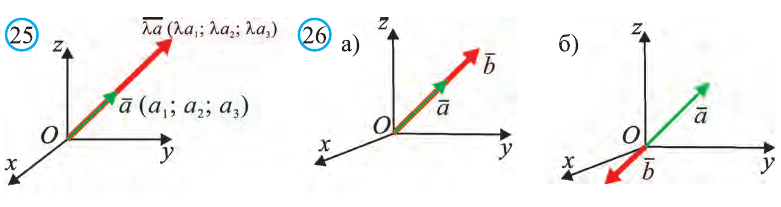
Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 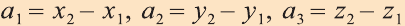, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

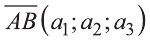
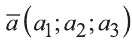
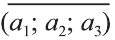
Hа основании этого вектор можно обозначить как или или кратко (рис. 18).

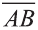
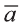
Вектор можно записать и без координат (или ). В этой записи

на первом месте начало вектора, а на втором — конец.

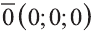
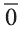
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают или , направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

а₂ и а₃ — координаты точки А, то есть А (а₁; а₂; а₃), то эти же числа будут

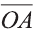
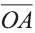
координатами вектора : (а₁; а₂; а₃).

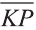
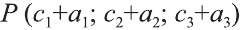
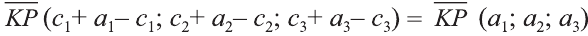
Однако вектор в пространстве с началом в точке К(с₁; с₂; с₃) и концом в точке будет иметь те же координаты: .

Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора 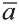записывают

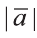
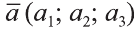
так. Длина вектора , заданного координатами,

вычисляется по формуле .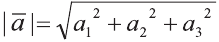

Пример:

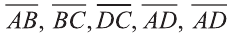
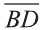
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов и равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

Следовательно, .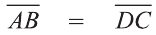

Докажите самостоятельно, что

Действия над векторами в пространстве

Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

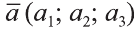
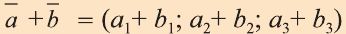
Суммой векторов и (b₁; b₂; b₃); называют вектор (рис. 20).

Пусть кран на рисунке 20.b движется вдоль вектора , а груз относительно крана вдоль вектора . В результате груз движется вдоль вектора . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

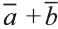
Свойства суммы векторов

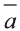
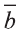
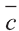
Для любых векторов , и имеют место следующие свойства:

a) — переместительный закон сложения векторов;

b) — распределительный закон сложения.

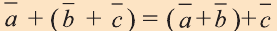
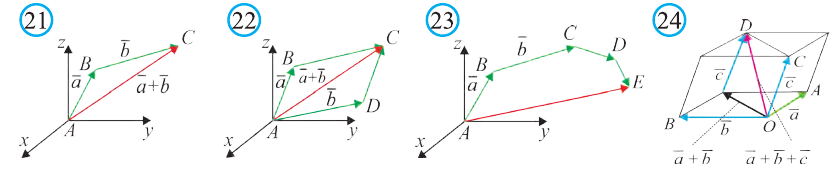
Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):

Правило параллелограмма сложения векторов

Если АВСD — параллелограмм (рис. 22), то

Правило многоугольника сложения векторов

Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то

Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

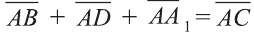
Вектор ​​​​​​= (a1; a₂; a₃) — называют умножением вектора

(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

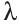
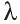
Для любых векторов и и чисел и

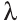
а);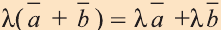

b);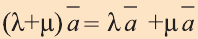

c)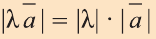 и направление вектора

совпадает с направлением вектора , если ,

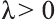
противоположно направлению вектора , если .

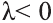
Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и . Если векторы

и сонаправлены или противоположно направлены,

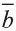
то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство , то они коллинеарны и наоборот.

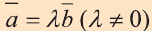
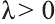
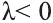
Если , то векторы и сонаправлены , если, то

противоположно направлены .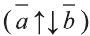

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

и наоборот.

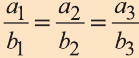
Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда (х — 1 ;у — 1; — 1).

По условию задачи векторы (х — 1 ;у — 1; — 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .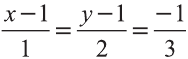

Откуда находим , .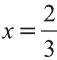

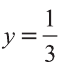
Итак,

Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).

Векторы (1; 0; 0), (0; 1; 0) и (0; 0; 1) называют ортами (рис. 28).

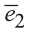
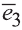
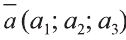
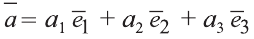
Любой вектор можно единственным образом разложить по ортам, то есть представить в виде (рис. 29).

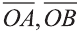
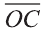
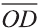
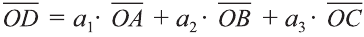
Точно также, если заданы три нeкомпланарных вектора и , то любой вектор можно единственным образом представить в виде:

.

Здесь 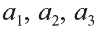некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и =, исходящих из точки О (рис. 30).

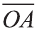
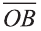
Угол между векторами и обозначают так .

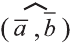
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

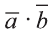
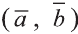
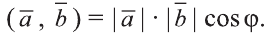
Скалярное произведение обозначают или . По определению (1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

В физике работа A, выполненная при движении тела на расстоянии , под воздействием силы (рис. 31), равна скалярному произведению силы на расстояние:

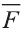
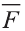
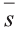
Свойство. Если 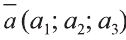и (b₁; b₂; b₃), то () =

Доказательство. Приложим векторы 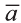и к началу

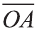
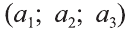
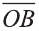
координат О (рис.32). Тогда = и = (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

Тогда .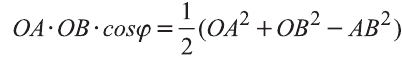

Однако, ,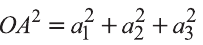

и .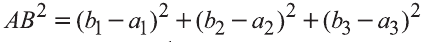

Следовательно,

.

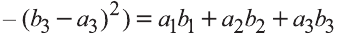
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 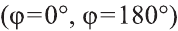, также выполняется

это равенство.

Свойства скалярного произведения векторов

1. — переместительное свойство.

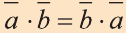
2. — распределительное свойство.

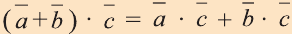
3. — сочетательное свойство.

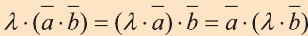
4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 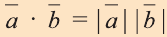, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 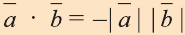, так как cos l80° = -1.

6. .

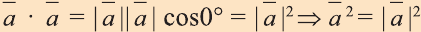
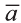
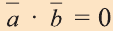
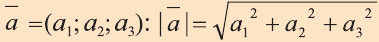
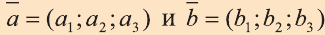
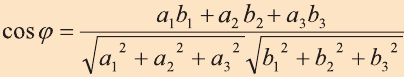
7. Если вектор перпендикулярен вектору , то . Следствия: а) Длина вектора ; (1) b) косинус угла между векторами

: ; (2)

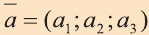
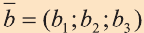
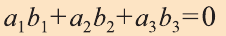
с) условие перпендикулярности векторов и

.

(3)

Пример:

— заданные точки. Найдите косинус угла между векторами .

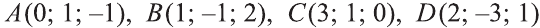
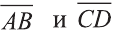
Решение:

Найдём длины векторов :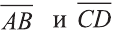

,

.

,

.

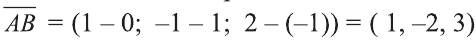
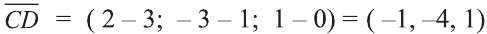
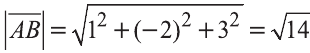
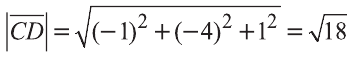
Следовательно,

Пример:

Найдите угол между векторами .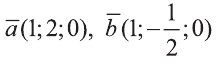

Решение:

Итак,

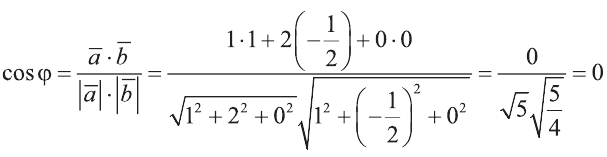
Пример:

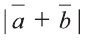
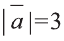
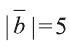
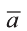
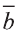
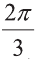
Найдите , если , и угол между векторамии равен .

Решение:

Пример:

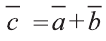
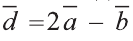
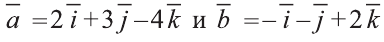
Найдите координаты и длины векторов 1); 2), если .

Решение:

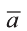
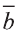
Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

. Следовательно,.

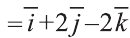
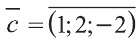
Тогда.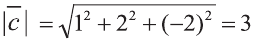

2)

.

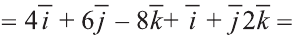
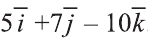
Следовательно, .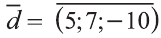

Тогда

• Заказать решение задач по высшей математике

Пример:

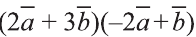
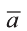
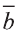
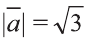
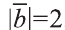
Найдите произведение, если угол между векторами и равен 30° и , .

Решение:

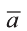
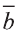
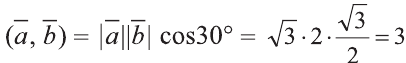
Сначала найдём поизведение векторов и :

.

Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

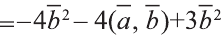
Учитывая, что ,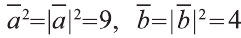

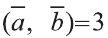
найдём искомое произведение

Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

Простейшим примером движения является параллельный перенос.

Пусть в пространстве даны вектор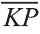 и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

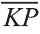
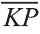
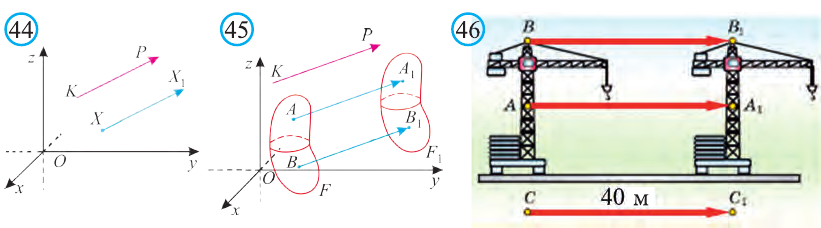
переносом на вектор , если выполняется условие . Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,

и т. д.

Пусть точка 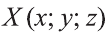фигуры F перешла в точку

фигуры F₁ при помощи параллельного переноса

на вектор .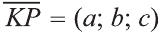

Тогда по определению получим:

или

.

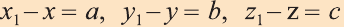
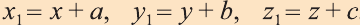
Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор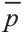 = (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .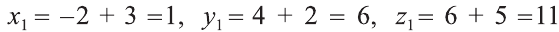

Ответ: .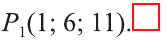

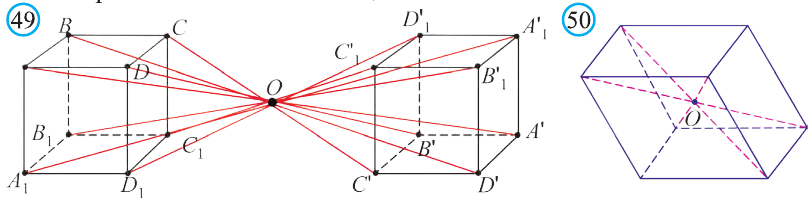
Центральная симметрия в пространстве

Если в пространстве 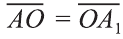, то есть точка О — середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) — искомая точка. По определению точка

О — середина отрезка АА₁. Следовательно,

Из этих уравнений получаем:

.

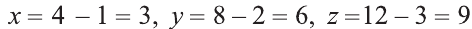
Ответ:

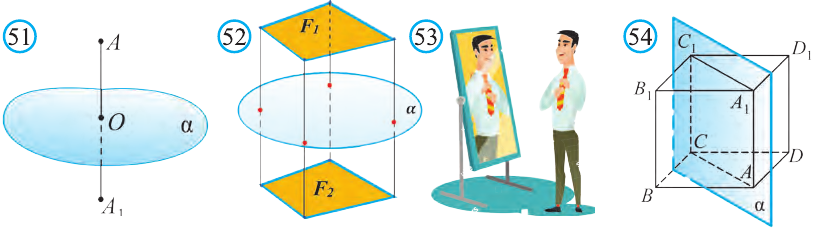
Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.

Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

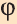
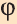
Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

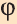
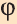
Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

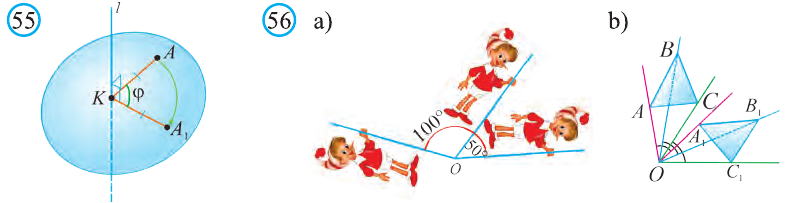
Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

Подобие пространственных фигур

Пусть 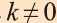и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 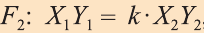, то это преобразование называют преобразованием подобия (рис. 59).

Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

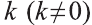
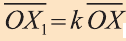
Пусть в пространстве задана фигура F, точка О и число к . Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию , называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость — в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.