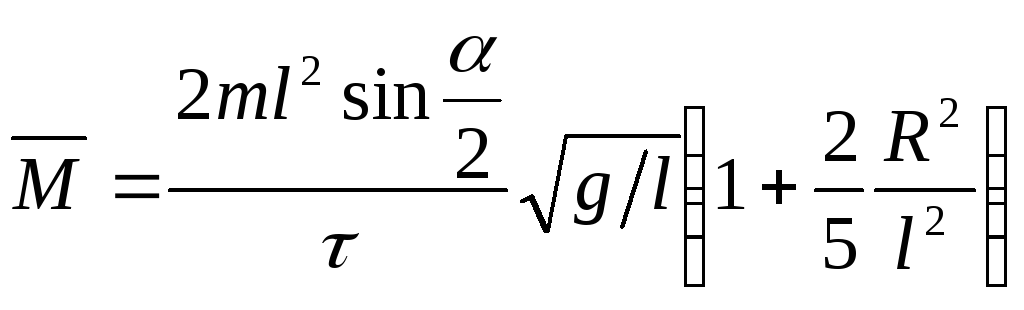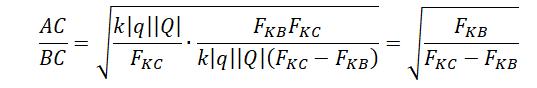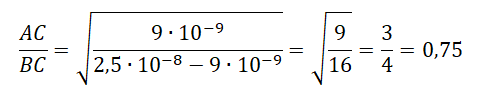Еще в древности было известно, что наэлектризованные тела взаимодействуют. Силу взаимодействия двух небольших заряженных шариков с помощью крутильных весов впервые измерил Шарль Кулон. Он сформулировал закон, который позже назвали его именем.
Так же, было выяснено, что сила, с которой два заряда притягиваются, или отталкиваются, зависит не только от самих зарядов, но и от вещества, в котором эти заряды находятся.
Опыт Кулона
Кулон нашел способ измерить взаимное действие двух зарядов. Для этого он использовал крутильные весы.
Ему не пришлось применять дополнительную особо чувствительную аппаратуру. Потому, что взаимное действие зарядов имело достаточную для наблюдения интенсивность.
Примечание: Опыт Кулона похож на опыт Кавендиша, который экспериментально определил гравитационную постоянную G.
Устройство крутильных весов
Такие весы (рис. 1) содержат перекладину — тонкий стеклянный стержень, расположенный горизонтально. Он подвешен на тонкой вертикально натянутой упругой проволоке.
На одном конце стержня находится небольшой металлический шарик. К другому концу прикреплен груз, который используется, как противовес.
Еще один металлический шарик, прикрепленный ко второй палочке из стекла, можно располагать неподалеку от первого шарика. Для этого в верхней крышке корпуса весов проделано отверстие.
Рис. 1. Устройство крутильных весов, использованных Кулоном для обнаружения силы взаимодействия зарядов
Если наэлектризовать шарики, они начнут взаимодействовать. А прикрепленная к проволоке перекладина, на которой находится один из шариков, будет поворачиваться на некоторый угол.
На корпусе весов на уровне палочки располагается шкала с делениями. Угол поворота связан с силой взаимного действия шариков. Чем больше угол поворота, тем больше сила, с которой шарики действуют друг на друга.
Чтобы сдвинувшийся шарик вернуть в первоначальное положение, нужно закрутить проволоку на некоторый угол. Так, чтобы сила упругости скомпенсировала силу взаимодействия шариков.
Для закручивания проволоки в верхней части весов есть рычажок. Рядом с ним расположен диск, а на нем – еще одна угловая шкала с делениями.
По нижней шкале определяют точку, в которую необходимо вернуть шарик. Верхней шкалой пользуются, чтобы установить угол, на который нужно рычажком закрутить проволоку.
С помощью крутильных весов Шарль Кулон выяснил, как именно сила взаимного действия зависит от величины зарядов и расстояния между зарядами.
В те годы единиц для измерения заряда не было. Поэтому ему пришлось изменять заряд одного шарика с помощью метода половинного деления.
Когда он касался заряженным шариком второго такого же шарика, заряды между ними распределялись поровну. Таким способом, можно было уменьшать заряд одного из шариков, участвующих в опыте, в 2, 4, 8, 16 и т. д. раз.
Так опытным путем Кулон получил закон, формула которого очень похожа на закон всемирного тяготения.
В память о его заслугах, силу взаимодействия зарядов называют Кулоновской силой.
Закон Кулона для зарядов в вакууме
Рассмотрим два точечных заряда, которые находятся в вакууме (рис. 2).
Рис. 2. Два положительных заряда q и Q, расположенных в вакууме на расстоянии r, отталкиваются. Силы отталкивания направлены вдоль прямой, соединяющей заряды
На рисунке 2 сила (large F_{Q} ) – это сила, с которой положительный заряд Q отталкивает второй положительный заряд q. А сила (large F_{q} ) принадлежит заряду q, с такой силой он отталкивает заряд Q.
Примечание: Точечный заряд – это заряженное тело, размером и формой которого можно пренебречь.
Силы взаимодействия зарядов, по третьему закону Ньютона, равны по величине и направлены противоположно. Поэтому, для удобства можно ввести обозначение:
[large F_{q} = F_{Q} = F]
Для силы взаимодействия зарядов в вакууме Шарль Кулон сформулировал закон так:
Два точечных заряда в вакууме,
взаимодействуют с силой
прямо пропорциональной
произведению величин зарядов
и обратно пропорциональной
квадрату расстояния между ними.
Формула для этого закона на языке математики запишется так:
[large boxed { F = k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;
(|q| left( text{Кл}right) ) – величина первого заряда;
(|Q| left( text{Кл}right) ) – величина второго заряда;
(r left( text{м}right) ) – расстояние между двумя точечными зарядами;
(k ) – постоянная величина, коэффициент в системе СИ;
Сила – это вектор. Две главные характеристики вектора – его длина и направление.
Формула позволяет найти одну из характеристик вектора F — модуль (длину) вектора.
Чтобы определить вторую характеристику вектора F – его направление, нужно воспользоваться правилом: Мысленно соединить два неподвижных точечных заряда прямой линией. Сила, с которой они взаимодействуют, будет направлена вдоль этой прямой линии.
Сила Кулона – это центральная сила, так как она направлена вдоль прямой, соединяющей центры тел.
Примечание: Еще один пример центральной силы — сила тяжести.
Что такое коэффициент k с точки зрения физики
Постоянная величина (k ), входящая в формулу силы взаимодействия зарядов, имеет такой физический смысл:
(k ) — это сила, с которой отталкиваются два положительных точечных заряда по 1 Кл каждый, когда расстояние между ними равно 1 метру.
Значение постоянной k равно девяти миллиардам!
[large boxed { k = 9cdot 10^{9} left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right) } ]
Это значит, что заряды взаимодействуют с большими силами.
Рис. 3. Коэффициент k в формуле взаимодействия зарядов
Константу k можно вычислить опытным путем, расположив два известных заряда (не обязательно по 1 Кулону каждый) на удобном для измерений расстоянии (не обязательно 1 метр) и измерив силу из взаимного действия.
Нужно подставить известные величины зарядов, расстояние между ними и измеренную силу в такую формулу:
[large boxed { k = frac {F cdot r^{2}}{|q| cdot |Q|} } ]
Величина k связана с электрической постоянной (varepsilon) такой формулой:
[large boxed { k = frac{1}{4pi cdot varepsilon_{0}} } ]
Поэтому дробь из правой части этой формулы можно встретить в различных справочниках физики, где она заменяет коэффициент k.
Закон Кулона для зарядов в веществе
Если два точечных заряда находятся в веществе, то сила их взаимного действия будет меньше, чем в вакууме. Для зарядов в веществе закон Кулона выглядит так:
[large boxed { F = frac{1}{varepsilon} cdot k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила взаимодействия зарядов в веществе;
(|q| ; |Q| left( text{Кл}right) ) – величины зарядов;
(r left( text{м}right) ) – расстояние между зарядами;
( k = 9cdot 10^{9} ) – постоянная величина;
( varepsilon ) – диэлектрическая проницаемость вещества, для разных веществ различается, ее можно найти в справочнике физики;
Рис. 4. Два заряда -q и +Q, расположенные в вакууме на расстоянии r, притягиваются сильнее, нежели те же заряды, расположенные на таком же расстоянии в диэлектрике
Силы, с которыми заряды действуют друг на друга в веществе, отличаются от сил взаимодействия в вакууме в ( varepsilon ) раз:
[large boxed { F_{text{(в диэлектрике)}} = frac{1}{varepsilon} cdot F_{text{(в вакууме)}} } ]
Примечание: Читайте отдельную статью, рассказывающую, что такое диэлектрическая проницаемость и электрическая постоянная.
В случае шаров равной массы m1 = m2 = m из (6) следуют простые соотношения v1 = v2,0 = 0; v2 = v1,0 = 0. Подставляя эти значения в (4), получаем: средние за
время удара значения сил взаимодействия между шарами:
F12
= -mv/t; F21
= mv/t(7)
Применим закон сохранения
механической энергии при движении правого шара до удара
(рис.1):
mgl(1 — cosa) =
mv2/2 (8)
Из
(7) и (8) находим
F12 =F21 = 2msin(a/2)Ögl/t(9)
Отметим, что реальный удар не является абсолютно
упругим, поэтому часть механической энергии системы перейдет в другие виды
энергии, например, в теплоту. Доля механической энергии, перешедшей в другие
виды энергии, может быть оценена по формуле
(Wнач -Wкон)/Wнах = (cosa’ — cosa)/1 — cosa(10)
Здесь a’ — угол
отклонения левого шара после удара.
3.
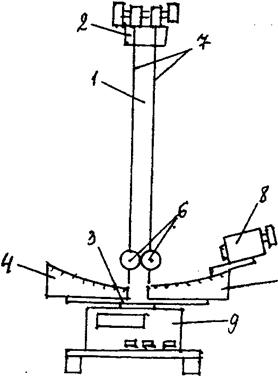
Описание экспериментальной установки.
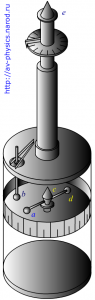
Экспериментальная
установка представлена на рис.2. На вертикальной стойке 1 закреплены верхний 2
и нижний 3 кронштейны. На нижнем кронштейне закреплены левая 4 и правая 5
шкалы. По правой шкале определяется начальный угол отклонения правого шара, по
левой — угол отклонения левого шара после соударения. Стальные шары 6 подвешены
с помощью токопроводящих подвесов 7 на штанге кронштейна 2. На правой шкале 5
смонтирован электромагнит 8. Электромагнит удерживает правый шар в выбранном
начальном положении. Миллисекундомер 9 предназначен для определения времени
соударения шаров контактным способом. В корпусе миллисекундомера смонтирован
также блок питания электромагнита.
Включение электромагнита происходит одновременно с
нажатием клавиши «Сеть» на панели миллисекундомера. При нажатии клавиши
«Пуск» электромагнит отключается от питания, шар освобождается. Счет
времени идет при наличии электрического контакта между шарами. Миллисекундомер
фиксирует только время первого соударения.
4. Порядок
выполнения работы.
1. Подключить установку к сети 220 В. Нажать на
клавишу «Сеть», при этом должны загореться лампочки цифровой
индикации на панели миллисекундомера.
2. Отклонить правый шар на угол a1 до соприкосновения с электромагнитом. Нажать клавишу
«Сброс». При этом лампы цифровой индикации на миллисекундомере
покажут нули.
3. Успокоив левый шар, нажать клавишу
«Пуск». При этом цепь электромагнита размыкается, правый шар
приходит в движение, происходит удар шаров. На индикаторе миллисекундомера
фиксируется время контакта (время соударения шаров). После удара необходимо
зафиксировать угол отклонения левого шара от положения равновесия. Значение a1’ этого угла и время соударения t1 записать в табл.1.
4. Пункты 2, 3 повторить не менее пяти раз. Результаты
записать в таблицу.
5. Пункты 2 — 4 повторить для другого значения
начального угла отклонения правого шара a2.
Углы a1 и a2 задает преподаватель. При проведении эксперимента
необходимо следить, чтобы шары двигались в одной вертикальной плоскости (удар
должен быть прямым).
5. Данные установки и таблица
результатов измерений.
Массы шаров m1 = m2 = m =
120 г
Длина подвеса шаров l1 = l2 = l =
50 см
Ускорение свободного падения
g = 9,8 м/с.
Погрешность установки углов a1 и a2 не более
Δa = 0,25 град х 0,5
Таблица результатов
измерений.
|
№ |
a1 = |
a2 = |
||
|
t1, мс |
a1’, град |
t2, мс |
a2’, град |
|
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
||||
|
Средн. |
6. Обработка
результатов измерений.
1. Рассчитать средние
значения t1, t2.
2. По формуле (9) рассчитать
средние значения сил взаимодействия F1 и F2 между
шарами для случаев a1 и a2.
3. Рассчитать значения Δt1, Δt2, dt1, dt2.
4. Считая погрешности dm, dl, dg малыми, рассчитать относительные погрешности dF1 и dF2 по
формуле
dF = Ö1/4*ctg2a/2*(Δa)2 + dt2
Значение Δa взять в радианах.
5. Рассчитать абсолютные погрешности ΔF1 и ΔF2.
6. Записать результат расчета сил взаимодействия с
учетом погрешности и с указанием на доверительную вероятность.
7. Используя формулу (10), оценить долю
механической энергии, перешедшей в другие виды энергии в результате соударения.
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
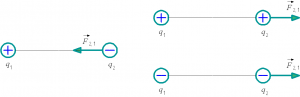
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Определение средней силы взаимодействия при ударе шаров равной массы
Постановка
задачи.
Определить среднюю силу взаимодействия
шаров равной массы m1=m2=m
при ударе. Угол начального отклонения
правого шара равен .
Длина подвесов l1=l2=l,
время соударения .
Указания
к решению.
Импульсы сил, действующих на шары, равны
(8.6)
Из
(8.6) при m1=m2=m,
1=2,0=0,
2=1,0=
получим
(8.7)
Здесь
F12
и F22
среднее за время удара значение сил
взаимодействия между шарами.
Применим
закон сохранения механической энергии
при движении правого шара до удара
(рис.8.1):
(8.8)
Из
(8.7) и (8.8) находим
(8.9)
О
тметим,
что реальный удар не является абсолютно
упругим, поэтому часть механической
энергии системыW
перейдет
в другие виды энергии (например, в
теплоту). Доля механической энергии,
перешедшей в другие виды энергии, может
быть оценена по формуле
(8.10)
Здесь
’
– угол отклонения левого шара после
удара.
Определение массы одного из шаров при их неупругом соударении
Постановка
задачи.
Два шара массами m1
и m2
подвешены на нитях так, что их центры
находятся на одном уровне. Правый шар
с известной массой m1
(рис.8.2) отклоняют на угол 1
и затем отпускают. При ударе шары
соединяются замком и движутся вместе
(осуществляется абсолютно неупругий
удар). Шары при этом отклоняются на угол
2.
Определить массу левого шара.
Указание
к решению. Применим
закон сохранения механической энергии
для определения скорости правого шара
в момент соударения:
(8.11)
Здесь
l
– длина подвеса. Так как проекция внешних
сил на ось 0х
равна нулю, можно воспользоваться
законом сохранения импульса в проекции
на ось 0х.
При неупругом ударе шаров получим
(8.12)
Здесь
U—
скорость обоих шаров после неупругого
удара.
Применим
закон сохранения механической энергии
при движении шаров после удара:
(8.13)
Решая систему
уравнений (8.11)-(8.13), получим соотношение
для определения массы левого шара
(8.14)
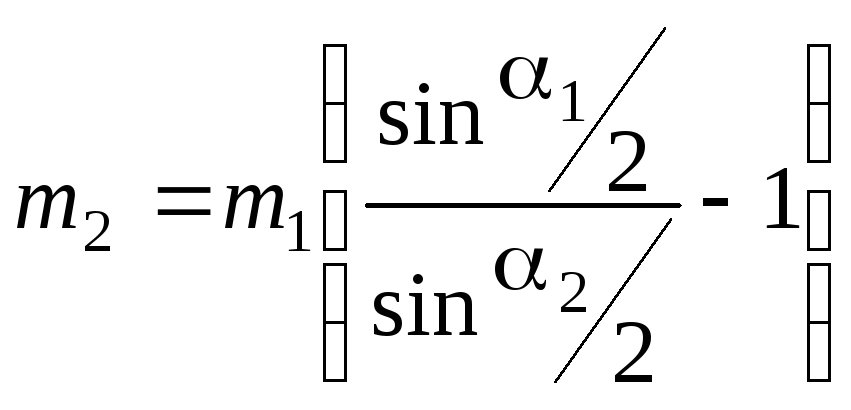
Определение среднего момента относительно точки подвеса, создаваемого силой, возникающей при взаимодействии упругих шаров
Постановка
задачи.
Определить средний момент сил, возникающий
при взаимодействии шаров равной массы
m1=m2=m,
равного радиуса R1=R2=R
при упругом ударе. Угол начального
отклонения правого шара равен ,
длины подвесов (до центров шаров) l1=l2=l
время соударения .
Указания
к решению. В
момент соударения правый шар обладал
моментом импульса относительно точки
подвеса, равным L=I,
где момент инерции I
согласно теореме Гюйгенса- Штейнера
равен
(2.15)
Используя
(2.8), найдем
(2.16)
Из
основного закона динамики вращательного
движения следует
(2.17)
Подставляя во
второе соотношение (2.17) соотношения
(2.15) и (2.16), получим среднее значение
момента силы
8.3. Схема абсолютно упругого удара 8.4. Область существенного смятия при абсолютно упругом ударе двух шаров
Определение средней силы взаимодействия соударяющихся шаров по радиусу площади их смятия в момент соударения
Постановка
задачи. Определить
среднюю длину взаимодействия шаров
равной массы m1=m2=m,
равного радиуса R1`=R2=R
при упругом ударе. Угол начального
отклонения правого шара равен ,
длины подвесов (до центра масс шаров)
l1=l2=l,
модули упругости материала шаров
E1=E2=E,
коэффициенты Пуассона 1=2=.
Указание
к решению. В
момент абсолютно упругого удара
происходит смятие шаров за счет
возникающих при ударе сил упругости
(рис.8.3). Здесь R—
радиус шаров, f-стрелка
смятия, u=2f
—
сближение центров шаров в момент удара,
2а—
диаметр площади смятия.
Из
геометрических соображений (см. рис.8.3)
(8.18)
Учитывая, что угол
мал, оставляем
лишь правые два члена в разложении
Из
малости
следует также
Отсюда
из (8.18) получим
(8.19)
Отметим,
что соотношение (8.19) имеет смысл лишь
при u<<R.
На
площади смятия вследствие действия
внешних сил возникает напряжение (сила,
действующая на единицу площади)
Отсюда,
используя известный закон Гука =
/ Е, получим выражение для относительной
деформации
(рис.8.4):
Точнее, с учетом
трехмерного обжатия со стороны
недеформированных частей шара
где -
коэффициент Пуассона. Стрелки смятия
f
a
. (8.20)
Используя выражение
(8.19) и (8.20),
определим размер радиуса смятия:
.
(8.21)
Заметим, что точное
выражение имеет вид
.
Отсюда можно
оценить среднюю силу взаимодействия
при ударе
Fa3
(8.22)
Указание: для
получения отпечатка площади смятия
между шарами следует вложить между ними
папиросную бумагу с копировальной.
Размеры отпечатка определяются с помощью
специального микроскопа.
Проверка
формулы Герца для соударяющихся упругих
шаров
Постановка
задачи. Применяя
закон сохранения энергии в процессе
соударения упругих шаров и учитывая
нелинейный характер задачи (силы
упругости растут с ростом радиуса смятия
и с увеличением сближения шаров, Генрих
Герц вывел соотношение (подробнее можно
познакомиться с задачей Герца в книге[8])
между временем соударения и скоростью
налетающего шара:
(1/)1/5.
Здесь —
время соударения; —
скорость налетающего шара.
Указания
к решению. Скорость
шара в момент начала соударения
определяется из рис. 8.1. Задача решается
с использованием закона сохранения
энергии. Пусть в первый момент
соприкосновения шаров механическая
энергия
.
Тогда по мере взаимодействия и сближения
шаров растет потенциальная энергия
взаимодействия, а кинетическая энергия
движущегося шара убывает. Из закона
сохранения механической энергии имеем
(8.23)
Зависимость
силы упругости от сближения шаров u
получаем из (2.21)
F(-u3/2).
Из
известного соотношения между потенциальной
энергией и силой упругости
получим
Wпотu5/2;
Wпот=ku5/2.
(8.24)
Здесь
коэффициент пропорциональности k
зависит от радиуса шаров и свойств
материала. Из (8.23)
и (8.24)
получим уравнение
(8.25)
Максимальное
сближение шаров достигается при du/dt0.
Решив уравнение (8.25), определим время
,
в течение которого длится соударение
(при этом u
меняется от 0 до umas
и обратно). Хотя уравнение (8.25) легко
решается разделением переменных, закон
Герца запишем без вывода
.
Здесь,
как и ранее, коэффициент пропорциональности
зависит от масс и размеров шаров, свойств
материала. Для проверки закона Герца
следует построить график, где по оси
абсцисс отложить 0,
а по оси ординат произведение 20.
Указание:
при малых углах
возможна замена sin.
Отметим, что
надо рассчитать в радианах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электризация и электрический заряд
Определения
Электростатика — раздел физики, изучающий неподвижные заряды.
Электризация — процесс, в результате которого тело приобретает электрический заряд. Если тело начиняет притягивать к себе другие тела, то говорят, что оно наэлектризовано, или приобрело электрический заряд.
Электрический заряд — физическая величина, определяющая способность тел участвовать в электромагнитных взаимодействиях.
Электрический заряд обозначается как q. Единица измерения — Кулон (Кл).
В природе существуют два вида зарядов, которые условно назвали положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются.
Закон сохранения зарядаАлгебраическая сумма зарядов в замкнутой системе сохраняется:
∑qi=const.
Замкнутая система в электростатике — такая система, которая не обменивается зарядами с окружающей средой.
Экспериментально доказано, что заряды можно делить, но до определенного предела. Носитель наименьшего электрического заряда — электрон. Он заряжен отрицательно.
Заряд электрона:
qe=−1,6·10−19 Кл
Масса электрона:
me=9,1·10−31 кг
Модуль любого заряда кратен заряду электрона:
q=Nqe
N — избыток электронов.
В процессе электризации от одного тела к другому передаются только электроны. Если у тела избыток электронов, то оно заряжено отрицательно, а если недостаток, то — положительно.
Внимание! Заряженные тела притягивают к себе нейтральные тела и тела с противоположным зарядом. Отталкивание наблюдается только между одноименно заряженными телами.
Пример №1. На двух одинаковых металлических шарах находятся положительный заряд 7 нКл и отрицательный заряд 1 нКл. Каким станет заряд на каждом шаре при соприкосновении шаров?
После того, как шары соприкоснутся, заряд на них выровняется. Так как большим зарядом обладает положительно заряженный шар, то оба шара в итоге будут заряжены положительно:
(7 – 1)/2 нКл = 3 нКл
Каждый шар будет иметь положительный заряд, равный 3 нКл.
Закон Кулона
Закон Кулона — основной закон электростатики, который был открыт экспериментально в 1785 году.
Закон Кулона
Два неподвижных точечных заряда в вакууме взаимодействуют друг с другом с силой, прямо пропорциональной квадрату расстояния между ними:
FK=k|q1||q2|r2
FK — сила, с которой взаимодействуют два точечных заряда (кулоновская сила, или сила Кулона). |q1| (Кл) и |q2| (Кл) — модули зарядов, r (м) — расстояние между зарядами, k — коэффициент пропорциональности, который численно равен силе взаимодействия между двумя точечными зарядами по 1 Кл, находящимися на расстоянии 1 м друг от друга:
k=14πε0=9·109 Н·м2/Кл2
ε0 — электрическая постоянная равная, 8,85∙10–12 Кл2/(Н∙м2).
Закон Кулона в среде
FK=k|q1||q2|εr2
ε — диэлектрическая проницаемость. Это табличная величина, которая показывает, во сколько раз электрическое взаимодействие в среде уменьшается по сравнению с вакуумом.
Направление силы Кулона
Направление силы Кулона зависит от знаков зарядов. На рисунке ее прикладывают к центру заряженного тела.
Подсказки к задачам
Подсказка №1
При соприкосновении одинаковых проводящих шариков, один из которых заряжен, заряд между шариками делится поровну:
q′
1=q′2=q2
Подсказка №2
При соприкосновении одинаковых проводящих шаров заряды складываются с учетом знаков и делятся поровну. Модули зарядом двух шариков:
q′1=q′2=|q1±q2|2
Пример №2. Два маленьких одинаковых металлических шарика заряжены положительными зарядами q и 5q и находятся на некотором расстоянии друг от друга. Шарики привели в соприкосновении и раздвинули на прежнее расстояние. Как изменилась сила взаимодействия шариков?
Изначально сила Кулона была равна:
FK1=kq5qr2=5kq2r2
Когда шарики коснулись, заряд каждого из них стал равен:
q′=5q+q2=3q
После того, как шарики раздвинули на прежнее расстояние, сила взаимодействия между ними стала равна:
FK2=k3q3qr2=9kq2r2
Поделим вторую силы на первую и получим:
FK2FK1=9kq2r2·r25kq2=95=1,8
Следовательно, после всех манипуляций сила взаимодействия между двумя заряженными шариками увеличилась в 1,8 раз.
Задание EF17493
Точечный отрицательный заряд q помещён слева от неподвижных положительно заряженных шариков (см. рисунок). Куда направлена равнодействующая кулоновских сил, действующих на заряд q?
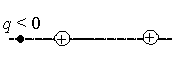
а) вверх
б) вниз
в) вправо
г) влево
Алгоритм решения
- Вспомнить, как взаимодействуют разноименные заряды.
- Установить взаимодействие заряда с каждым из шариков.
- Выяснить, куда будет направлена равнодействующая сила, действующая на заряд со стороны заряженных шариков.
Решение
Отрицательные и положительные заряды притягиваются. Следовательно, каждый из положительно заряженных шариков притягивает отрицательный заряд q к себе — каждая из сил (FK1 и FK2) будет направлена вправо. Поэтому их равнодействующая FK тоже будет направлена вправо.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17545
В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
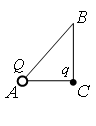
а) 0,36
б) 0,60
в) 0,75
г) 1,67
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона для данного случая.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину С: FKC = 2,5∙10–8 Н.
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину В: FKB = 9∙10–9 Н.
Запишем закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона для 1 и 2 случая:
FKC=k|q||Q|AC2
FKB=k|q||Q|AB2
По условию задачи нужно найти соотношение сторон треугольника АС к ВC. Для этого выразим известные стороны треугольника из формул выше:
AC=√k|q||Q|FKC
AB=√k|q||Q|FKB
Сторону ВС можно выразить с помощью теоремы Пифагора (АВС — прямоугольный треугольник, так как угол С является прямым):
BC=√AB2−AC2=√k|q||Q|FKB−k|q||Q|FKC=√k|q||Q|(FKC−FKB)FKBFKC
Отсюда:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17737
На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных знаков. Если их шары соединить проволокой, то показания обоих электрометров
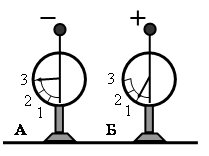
Ответ:
а) не изменятся
б) станут равными 1
в) станут равными 2
г) станут равными 0
Алгоритм решения
1.Записать показания электрометров.
2.Установить, что произойдет, если их соединить проволокой.
3.Вычислить показания электрометров после их соединения.
Решение
Запишем показания электрометров:
• Слева электрометр показывает отрицательный заряд q1, равный «3».
• Справа электрометр показывает положительный заряд q2, равный «1».
Когда электрометры соединятся проволокой, избыточный отрицательный заряд в виде электронов частично переместится из левого электрометра в правый электрометр так, что показания приборов выровняются. Они будут показывать:
q=|−q1+q2|2=22=1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.6k