Содержание
- 1 Магнитное поле планеты
- 2 Почему Марс потерял магнитное поле
- 3 Расчет марсианской гравитации
- 4 Почему на Марсе по другому
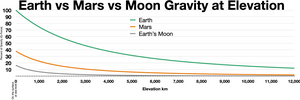
- 5 Сравнение с гравитацией Земли
После покорения Луны Марс стал главным объектом программ, нацеленных на достижение и освоение новых космических рубежей. Расположенный в «зоне жизни», где солнечной энергии достаточно для существования организмов земного типа, он — лучший из вариантов для колонизации. Но проблемы с гравитацией на Марсе и с отсутствием защиты от любых видов излучения заставляют откладывать воплощение уже готовых проектов.
Планета Марс. Credit: Zen
Магнитное поле планеты
Одним из непреодолимых пока препятствий становится отсутствие на Марсе планетарной магнитосферы. Остаточные явления магнетизма присутствуют и колеблются, по данным российских исследовательских станций, от 60 гамм на экваторе до 120 — на полюсах, но это более чем в 500 раз меньше напряженности земного аналога.
Задача магнитного поля любой планеты — защитить ее от атак солнечного ветра и космической радиации, с чем фрагментарные проявления справиться не в состоянии. Это свидетельствует о том, что железное ядро планеты находится в неподвижном состоянии по отношению к коре.
Вращение земного ядра создает в расплавленной магме конвекционные токи, которые генерируют магнитную напряженность (по принципу динамо-машины). На красной планете этот механизм не работает, что сначала привело к исчезновению почти всей марсианской атмосферы, а сейчас проявляется в постоянном уровне радиации в 220 рад в день на поверхности.
Это на 10% больше нормы, допустимой для космонавтов на МКС, и для возможных колонистов грозит необратимыми последствиями:
- повышенным риском онкологических заболеваний;
- изменениями на генетическом уровне;
- мутациями в последующих поколениях;
- острой лучевой болезнью и смертью.
Тем не менее существуют явные признаки, что когда-то магнитное поле Марса существовало и функционировало, но процесс этот прекратился в силу неизвестных обстоятельств около 3,2 млрд лет назад.
Почему Марс потерял магнитное поле
Из версий о причинах утраты магнитосферы наиболее убедительной считается гипотеза профессора Джафара Аркани-Хамеда из университета в Торонто. Проведя компьютерное моделирование, он доказал высокую вероятность того, что катастрофа связана со взаимодействием планет солнечной системы, в частности с влиянием Юпитера на пояс астероидов.
Под влиянием этого газового гиганта достаточно массивное тело, сопоставимое по размерам с малой планетой, было вытолкнуто со своей орбиты и, захваченное Марсом, сделалось его спутником с постоянно уменьшающимся радиусом обращения.
При снижении спутника до 50-75 тыс. км возникла конвекционная нестабильность марсианского ядра, что привело его в движение, создав эффект динамо. Возникло общепланетное магнитное поле, которое могло просуществовать до 400 млн лет, надежно прикрывая планету.
Однако сила притяжения Марса продолжала действовать на астероид, заставляя его снижаться до тех пор, пока на пределе Роша (2,44 радиуса планеты) он не разрушился и обломки его не рухнули на поверхность.
Две стороны планеты Марс. Credit: Rock-cafe
Марс получил из космоса удар такой силы, что деформировалась твердая кора планеты.
Астрономы находят этому подтверждение в наличии гигантского кратера в области Эллада (южное полушарие) и антиподной ей группе вулканов во главе с крупнейшей в солнечной системе горой Олимп (северное), поднимающейся над окружающей равниной на 26 км.
Утрата спутника повлекла за собой остановку вращения ядра и исчезновение планетарного поля. Остаточные магнитные явления неравномерно распределились по поверхности Марса и связаны, скорее всего, с особенностями геологических пород.
Расчет марсианской гравитации
Из-за слабого и неравномерного распределения магнетизма по поверхности планеты показатели его гравитации тоже крайне низки.
Сила тяжести на Марсе составляет 38% от земной, что легко рассчитывается по формуле Ньютона:
g = m / r².
Соотношение марсианской массы (6,4171 х 10²³ кг) к массе Земли = 0,107, то есть около 10%. Тот же показатель для радиусов планет (3389,5 и 6371 соответственно) = 0,532.
g = 0,107 / 0,532² = 0,376.
То есть тело, имеющее на Земле в состоянии покоя вес 100 кг, на Марсе будет весить 38. А это заставляет вспомнить о негативном воздействии на организм человека слабой гравитации. Космонавты за 4-6 месяцев пребывания на МКС теряли до 15% мышечной массы при интенсивных нагрузочных упражнениях.
Гравитация Марса и Земли. Credit: 24Warez
Разрешающая способность современных космических аппаратов позволяет достичь красной планеты только за 8 месяцев. Кроме того, длительное нахождение в подобных условиях пагубно воздействует на плотность костей, сохранность внутренних органов, проявляется в снижении зрения.
Почему на Марсе по другому
Тяготение Марса относительно Земли выражается в пропорциональной зависимости следующих характеристик:
- массы;
- расстояния до центра планеты;
- размера;
- плотности.
Земля, имеющая превосходство по всем показателям, оказывает большую силу притяжения, которая ослабляется лишь по мере удаления планет друг от друга. Эти же параметры определяют и воздействие на предметы, находящиеся на поверхности каждой из них.
Несмотря на отдельные совпадения и частичное сходство, проявляющиеся в наличии полярных шапок, примерно одинаковом наклоне оси вращения, климатических изменениях, различия между планетами гораздо существенней.
Сила тяжести Марса относительно Земли. Credit: Theguestion
Сравнение с гравитацией Земли
Имея высокие гравитационные показатели, обладая достаточно плотной и высокой атмосферой, защищенная магнитным полем Земля создает для жизни организмов всех уровней оптимальные условия. Тогда как на Марсе недостаточная сила тяготения не в состоянии удержать на поверхности ни одной жидкости. Вода существует там только в твердом или газообразном состоянии.
Разреженная атмосфера, засушливый и холодный климат (средние температуры колеблются от -143ºC зимой до 30ºC летом), низкая гравитация и магнитное поле не допускают возможности присутствия на планете сложных биоструктур.
Исключение могут составлять бактерии и микроорганизмы, приспособляемость которых к самым экстремальным условиям доказана на практике. Они выживают в открытом космосе, при сверхнизких температурах и в радиоактивной воде атомных реакторов. Но для высших форм жизни условия Марса пока неприемлемы.
The gravity of Mars is a natural phenomenon, due to the law of gravity, or gravitation, by which all things with mass around the planet Mars are brought towards it. It is weaker than Earth’s gravity due to the planet’s smaller mass. The average gravitational acceleration on Mars is 3.72076 ms−2 (about 38% of that of Earth) and it varies.[1] In general, topography-controlled isostasy drives the short wavelength free-air gravity anomalies.[2] At the same time, convective flow and finite strength of the mantle lead to long-wavelength planetary-scale free-air gravity anomalies over the entire planet.[3][4] Variation in crustal thickness, magmatic and volcanic activities, impact-induced Moho-uplift, seasonal variation of polar ice caps, atmospheric mass variation and variation of porosity of the crust could also correlate to the lateral variations.[5][6][7][8][9] Over the years models consisting of an increasing but limited number of spherical harmonics have been produced. Maps produced have included free-air gravity anomaly, Bouguer gravity anomaly, and crustal thickness. In some areas of Mars there is a correlation between gravity anomalies and topography. Given the known topography, higher resolution gravity field can be inferred. Tidal deformation of Mars by the Sun or Phobos can be measured by its gravity. This reveals how stiff the interior is, and shows that the core is partially liquid.
The study of surface gravity of Mars can therefore yield information about different features and provide beneficial information for future landings.
Measurement[edit]
Rotating spherical harmonic, with 

To understand the gravity of Mars, its gravitational field strength g and gravitational potential U are often measured. Simply, if Mars is assumed to be a static perfectly spherical body of radius RM, provided that there is only one satellite revolving around Mars in a circular orbit and such gravitation interaction is the only force acting in the system, the equation would be
where G is the universal constant of gravitation (commonly taken as G = 6.674 × 10−11 m3 kg−1 s−2),[10] M is the mass of Mars (most updated value: 6.41693 × 1023 kg),[11] m is the mass of the satellite, r is the distance between Mars and the satellite, and 

Therefore, 
However, as Mars is a generic, non-spherical planetary body and influenced by complex geological processes, more accurately, the gravitational potential is described with spherical harmonic functions, following convention in geodesy; see Geopotential model.
[12]
where 








and is the associated Legendre polynomial with 

The coefficient 

- The lower the degree
and order
, the longer wavelength of anomaly it represents. In turn, long-wavelength gravity anomaly is influenced by global geophysical structures.
- The higher the degree
and order
, the shorter wavelength of anomaly it represents. For degree over 50, it has been shown that those variations have high correlation with the topography.[13] Geophysical interpretation of surface features could further help deriving a more complete picture of the Martian gravity field, though misleading results could be produced.[13]
The oldest technique in determining the gravity of Mars is through Earth-based observation. Later with the arrival of uncrewed spacecraft, subsequent gravity models were developed from radio tracking data.
Scientists measured the perturbation of different spacecraft through Doppler and range tracking methods to develop different gravity models ever since the first arrival of the uncrewed space probe Mariner 9 in 1971. (Credit: NASA’s Scientific Visualization Studio)
Earth-based observation[edit]
Before the arrival of the Mariner 9 and Viking orbiter spacecraft at Mars, only an estimate of the Mars gravitational constant GM, i.e. the universal constant of gravitation times the mass of Mars, was available for deducing the properties of the Martian gravity field.[14] GM could be obtained through observations of the motions of the natural satellites of Mars (Phobos and Deimos) and spacecraft flybys of Mars (Mariner 4 and Mariner 6).[14]
Long term Earth-based observations of the motions of Phobos and Deimos provide physical parameters including semi-major axis, eccentricity, inclination angle to the Laplacian plane etc.,[15] which allow calculation of the ratio of solar mass to the mass of Mars, moment of inertia and coefficient of the gravitational potential of Mars, and give initial estimates of the gravity field of Mars.[15]
Inferred from radio tracking data[edit]
Three-way Doppler, with signal transmitter and receiver separated
Precise tracking of spacecraft is of prime importance for accurate gravity modeling, as gravity models are developed from observing tiny perturbation of spacecraft, i.e. small variation in velocity and altitude. The tracking is done basically by the antennae of the Deep Space Network (DSN), with one-way, two-way and three-way Doppler and range tracking applied.[16] One-way tracking means the data is transmitted in one way to the DSN from the spacecraft, while two-way and three-way involve transmitting signals from Earth to the spacecraft (uplink), and thereafter transponded coherently back to the Earth (downlink).[16] The difference between two-way and three-way tracking is, the former one has the same signal transmitter and receiver on Earth, while the latter one has the transmitter and receiver at different locations on Earth.[16] The use of these three types of tracking data enhances the coverage and quality of the data, as one could fill in the data gap of another.[16]
Doppler tracking is a common technique in tracking the spacecraft, utilizing radial velocity method, which involves detection of Doppler shifts.[13] As the spacecraft moves away from us along line of sight, there would be redshift of signal, while for the reverse, there would be blueshift of signal. Such technique has also been applied for observation of the motion of exoplanets.[17] While for the range tracking, it is done through measurement of round trip propagation time of the signal.[13] Combination of Doppler shift and range observation promotes higher tracking accuracy of the spacecraft.
The tracking data would then be converted to develop global gravity models using the spherical harmonic equation displayed above. However, further elimination of the effects due to affect of solid tide, various relativistic effects due to the Sun, Jupiter and Saturn, non-conservative forces (e.g. angular momentum desaturations (AMD), atmospheric drag and solar radiation pressure) have to be done,[13] otherwise, considerable errors result.
History[edit]
|
|
This section is missing information about alternative nomenclature such as GMM-3 as mgm1025, used in some NASA papers and in its planetary data system. Please expand the section to include this information. Further details may exist on the talk page. (January 2022) |
The latest gravity model for Mars is the Goddard Mars Model 3 (GMM-3), produced in 2016, with spherical harmonics solution up to degree and order 120.[13] This model is developed from 16 years of radio tracking data from Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO), as well as the MOLA topography model and provides a global resolution of 115 km.[13] A separate free-air gravity anomaly map, Bouguer gravity anomaly map and a map of crustal thickness were produced along with this model.[13] Compared with MRO110C and other previous models, major improvement of the estimation of the gravity field comes from more careful modeling of the non-conservative forces applied to the spacecraft.[13]
| Gravity solutions | Authors | Year | Degree (m) and order (l) of the spherical harmonic solution
[Surface resolution (km)] |
Data source |
|---|---|---|---|---|
| – | JP Gapcynski, RH Tolson and WH Michael Jr | 1977 | 6[18] | Tracking data of Mariner 9, Viking 1 and 2 spacecraft[18] |
| Geoide martien[19] | G Balmino, B Moynot and N Vales | 1982 | 18[19]
[¬600 km] |
Tracking data of Mariner 9, Viking 1 and 2 spacecraft[19] |
| GMM-1[20] | DE Smith, FJ Lerch, RS Nerem, MT Zuber, GB Patel, SK Fricke and FG Lemoine | 1993 | 50[20]
[200–300 km] |
Tracking data of Mariner 9, Viking 1 and 2 spacecraft[20] |
| Mars50c[21] | AS Konopliv, WL Sjogren | 1995 | 50[21] | Tracking data of Mariner 9, Viking 1 and 2 spacecraft[21] |
| GMM-2B[14] | FG Lemoine, DE Smith, DD Rowlands, MT Zuber, GA Neumann, DS Chinn, and DE Pavlis | 2001 | 80[14] | Tracking data of Mars Global Surveyor (MGS), and MOLA-derived topography data [14] |
| GGM1041C[22] | FG Lemoine | 2001 | 90[22] | Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data[22] |
| MGS95J[23] | AS Konopliv, CF Yoder, EM Standish, DN Yuan, WL Sjogren | 2006 | 95[23]
[~112 km] |
Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data [23] |
| MGGM08A[7] | JC Marty, G Balmino, J Duron, P Rosenblatt, S Le Maistre, A Rivoldini, V Dehant, T. Van Hoolst | 2009 | 95[7]
[~112 km] |
Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data[7] |
| MRO110B2[24] | AS Konopliv, SW Asmar, WM Folkner, Ö Karatekin, DC Nunes, SE Smrekar, CF Yoder, MT Zuber | 2011 | 110[24] | Tracking data of Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO), and MOLA-derived topography data[24] |
| MGM2011[1] | C Hirt, SJ Claessens, M Kuhn, WE Featherstone | 2012 | [3 km (equator) – 125 km][1] | Gravity solution MRO110B2, and MOLA-derived topography data[1] |
| GMM-3[13] | A Genova, S Goossens, FG Lemoine, E Mazarico, GA Neumann, DE Smith, MT Zuber | 2016 | 120[13]
[115 km] |
Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO)[13]
|
The techniques in tracking the spacecraft and geophysical interpretation of surface features can affect the resolution of the strength of gravity field. The better technique favors spherical harmonic solutions to higher degrees and orders. Independent analysis on Mariner 9 and Viking Orbiter tracking data yielded a degree and order of 6 spherical harmonic solution.,[18] Further combination of the two data sets, along with correlation of anomalies with volcanic features (positive anomaly) and deep-printed depression (negative anomaly) assisted by image data allows a degree and order of 18 spherical harmonic solution produced.[19] Further use of spatial a priori constraint method, which had taken the topography into account in solving the Kaula power law constraint, had favored model of up to degree 50 spherical harmonic solution in global resolution (Goddard Mars Model-1, or GMM-1)[20] then the subsequent models with higher completeness and degree and order up to 120 for the latest GMM-3.[13]
Mars free-air gravity map produced along with the GMM-3 gravity solution[13] (Red: gravity high; Blue: gravity low) (Credit: NASA’s Scientific Visualization Studio)
Therefore, gravity models nowadays are not directly produced through transfer of the measured gravity data to any spatial information system because there is difficulty in producing model with sufficiently high resolution. Topography data obtained from the MOLA instrument aboard the Mars Global Surveyor thus becomes a useful tool in producing a more detailed short-scale gravity model, utilizing the gravity-topography correlation in short-wavelength.[13] However, not all regions on Mars show such correlation, notably the northern lowland and the poles.[13] Misleading results could be easily produced, which could lead to wrong geophysics interpretation.[13]
The later modifications of gravity model include taking other non-conservative forces acting on spacecraft into account, including atmospheric drag, solar radiation pressure, Mars reflected solar radiation pressure, Mars thermal emission, and spacecraft thrusting which despins or desaturates the angular moment wheels.[14] In addition, Martian precession and third body attraction due to the Sun, Moon and planets, which could affect the spacecraft orbit, as well as relavistic effects on the measurements should also be corrected.[7] These factors could lead to offset of the true gravity field. Accurate modeling is thus required to eliminate the offset. Such work is still ongoing.
Static gravity field[edit]
Many researchers have outlined the correlation between short-wavelength (locally varying) free-air gravity anomalies and topography. For regions with higher correlation, free-air gravity anomalies could be expanded to higher degree strength through geophysical interpretation of surface features,[13] so that the gravity map could offer higher resolution. It has been found that the southern highland has high gravity/topography correlation but not for the northern lowland.[13] Therefore, the resolution of free-air gravity anomaly model typically has higher resolution for the southern hemisphere, as high as over 100 km.[13]
Free-air gravity anomalies are relatively easier to measure than the Bouguer anomalies as long as topography data is available because it does not need to eliminate the gravitational effect due to the effect of mass surplus or deficit of the terrain after the gravity is reduced to sea level. However, to interpret the crustal structure, further elimination of such gravitational effect is necessary so that the reduced gravity would only be the result of the core, mantle and crust below datum.[5] The product after elimination is the Bouguer anomalies. However, density of the material in building up the terrain would be the most important constraint in the calculation, which may vary laterally on the planet and is affected by porosity and geochemistry of the rock.[5][9] Relevant information could be obtained from Martian meteorites and in-situ analysis.
Local gravity anomalies[edit]
The crust-mantle boundary variation, intrusion, volcanism and topography can bring effect to the orbit of spacecraft, due to the higher density of mantle and volcanic material and lower density of the crust. (Not in scale) +ve: Positive anomaly; -ve: Negative anomaly
Since Bouguer gravity anomalies have strong links with depth of crust-mantle boundary, one with positive Bouguer anomalies may mean that it has a thinner crust composed of lower density material and is influenced more strongly by the denser mantle, and vice versa. However, it could also be contributed by the difference in density of the erupted volcanic load and sedimentary load, as well as subsurface intrusion and removal of material.[5][6][25] Many of these anomalies are associated with either geological or topographic features.[5] Few exception includes the 63°E, 71°N anomaly,[5] which may represent an extensive buried structure as large as over 600 km, predated the early-Noachian buried surface.[5]
Topography anomalies[edit]
Strong correlation between topography and short-wavelength free-air gravity anomalies has been shown for both study of the gravity field of the Earth and the Moon,[2] and it can be explained by the wide occurrence of isostasy.[2][26] High correlation is expected for degree over 50 (short-wavelength anomaly) on Mars.[13] And it could be as high as 0.9 for degrees between 70 and 85.[13] Such correlation could be explained by flexural compensation of topographic loads.[2][26] It is noted that older regions on Mars are isostatically compensated when the younger region are usually only partially compensated.[13]
Anomalies from volcanic constructs[edit]
Mars Bouguer gravity map, produced along with GMM-3 gravity solution in 2016[13](Red: gravity high; Blue: gravity low) (Credit: NASA’s Scientific Visualization Studio)
Different volcanic constructs could behave differently in terms of gravity anomalies. Volcanoes Olympus Mons and the Tharsis Montes produce the smallest positive free-air gravity anomalies in the solar system.[5] Alba Patera, also a volcanic rise, north of the Tharsis Montes, however, produces negative Bouguer anomaly, though its extension is similar to that of Olympus Mons.[5] And for the Elysium Mons, its center is found to have slight increase in Bouguer anomalies in an overall broad negative anomaly context in the Elysium rise.[5]
The knowledge of anomaly of volcanoes, along with density of the volcanic material, would be useful in determining the lithospheric composition and crustal evolution of different volcanic edifices.[27] It has been suggested that the extruded lava could range from andesite (low density) to basaltic (high density) and the composition could change during the construction of the volcanic shield, which contributes to the anomaly.[27] Another scenario is it is possible for high density material intruded beneath the volcano.[27][6] Such setting has already been observed over the famous Syrtis major, which has been inferred to have an extinct magma chamber with 3300 kg m3 underlying the volcano, evident from positive Bouguer anomaly.[6]
Anomalies from depressions[edit]
Different depressions also behave differently in Bouguer anomaly. Giant impact basins like Argyre, Isidis, Hellas and Utopia basins also exhibit very strong positive Bouguer anomalies in circular manner.[5] These basins have been debated for their impact crater origin. If they are, the positive anomalies may be due to uplift of Moho, crustal thinning and modification events by sedimentary and volcanic surface loads after impacting.[5][25]
But at the same time there are also some large basins that are not associated with such positive Bouguer anomaly, for example, Daedalia, northern Tharsis and Elysium, which are believed to be underlain by the northern lowland plain.[5]
In addition, certain portions of Coprates, Eos Chasma and Kasei Valles are also found to have positive Bouguer anomalies,[5] though they are topographic depressions. This may suggest that these depressions are underlain by shallow dense intrusion body.[5]
Global gravity anomalies[edit]
Global gravity anomalies, also termed as long-wavelength gravity anomalies, are the low-degree harmonics of the gravity field,[4] which cannot be attributed to local isostasy, but rather finite strength of the mantle and density differences in the convection current.[13][3][4] For Mars, the largest component of Bouguer anomaly is the degree one harmonic, which represents the mass deficit in the southern hemisphere and excess in the northern hemisphere.[5] The second largest component corresponds to the planet flattening and Tharsis bulge.[5]
Early study of the geoid in the 1950s and 1960s has focused on the low-degree harmonics of the Earth’s gravity field in order to understand its interior structure.[4] It has been suggested that such long-wavelength anomalies on Earth could be contributed by the sources located in deep mantle and not in the crust, for example, caused by the density differences in driving the convection current,[4][28] which has been evolving with time. The correlation between certain topography anomalies and long-wavelength gravity anomalies, for example, the mid-Atlantic ridge and Carlsberg ridge, which are topography high and gravity high on the ocean floor, thus became the argument for the convection current idea on Earth in the 1970s,[29][30] though such correlations are weak in the global picture.
Another possible explanation for the global scale anomalies is the finite strength of the mantle (in contrast to zero stress), which makes the gravity deviated from hydrostatic equilibrium.[3] For this theory, because of the finite strength, flow may not exist for most of the region that are understressed.[3] And the variations of density of the deep mantle could be the result of chemical inhomogeneities associated with continent separations,[3] and scars left on Earth after the torn away of the moon.[3] These are the cases suggested to work when slow flow is allowed to happen under certain circumstances.[3] However, it has been argued that the theory may not be physically feasible.[4]
Time-variable gravity field[edit]
Sublimation-condensation cycle occurs on Mars which results in carbon dioxide exchange between the cryosphere and the atmosphere. In turn, there is exchange in mass between the two spheres, which gives seasonal variation of gravity. (Courtesy NASA/JPL-Caltech)
Seasonal change of gravity field at the poles[edit]
The sublimation-condensation cycle of carbon dioxide on Mars between the atmosphere and cryosphere (polar ice cap) operates seasonally.[8] This cycle contributes as almost the only variable accounting for changes in gravity field on Mars.[8] The measured gravitational potential of Mars from orbiters could be generalized as the equation below,
[8]
In turn, when there is more mass in the seasonal caps due to the more condensation of carbon dioxide from the atmosphere, the mass of the atmosphere would drop. They have inverse relationship with each other. And the change in mass has direct effect towards the measured gravitational potential.
The seasonal mass exchange between the northern polar cap and southern polar cap exhibits long-wavelength gravity variation with time.[8][13] Long years of continuous observation has found that the determination of even zonal, normalized gravity coefficient Cl=2, m=0, and odd zonal, normalized gravity coefficient Cl=3, m=0 are crucial for outlining the time-variable gravity due to such mass exchange,[24][8][31][32] where 

If we regard the two poles as two distinct point masses, then, their masses are defined as,
[32]
[32]
Data has indicated that the maximum mass variation of the southern polar cap is approximately 8.4 × 1015 kg,[13] occurring near the autumnal equinox,[13] while for that of the northern polar is approximately 6.2 × 1015 kg,[13] occurring in between the winter solstice and spring equinox.[13]
In long term speaking, it has been found that the mass of ice stored in North Pole would increase by (1.4 ± 0.5) × 1011 kg,[8] while in South Pole it would decrease by (0.8 ± 0.6) × 1011 kg.[8] In addition, the atmosphere would have decrease in term of the mass of carbon dioxide by (0.6 ± 0.6) × 1011 kg in long term as well.[8] Due to existence of uncertainties, it is unclear whether migration of material from the South Pole to the North Pole is ongoing, though such a possibility cannot be ruled out.[8]
Tide[edit]
The two major tidal forces acting on Mars are the solar tide and Phobos tide.[13] Love number k2 is an important proportional dimensionless constant relating the tidal field acting to the body with the multipolar moment resulting from the mass distribution of the body. Usually k2 can tell quadrupolar deformation.[13] Finding k2 is helpful in understanding the interior structure on Mars.[13] The most updated k2 obtained by Genova’s team is 0.1697 ± 0.0009.[13] As if k2 is smaller than 0.10 a solid core would be indicated, this tells that at least the outer core is liquid on Mars,[31] and the predicted core radius is 1520–1840 km.[31]
However, current radio tracking data from MGS, ODY and MRO does not allow the effect of phase lag on the tides to be detected because it is too weak and needs more precise measurement on the perturbation of spacecraft in the future.[13]
Geophysical implications[edit]
Crustal thickness[edit]
Histogram of percentage area against crustal thickness of Mars: 32 km and 58 km are the two major peaks of the histogram.
No direct measurement of crustal thickness on Mars is currently available. Geochemical implications from SNC meteorites and orthopyroxenite meteorite ALH84001 suggested that mean crustal thickness of Mars is 100–250 km.[33] Viscous relaxation analysis suggested that the maximum thickness is 50–100 km. Such thickness is critical in maintaining hemispheric crustal variations and preventing channel flow.[34] Combination studies on geophysics and geochemistry suggested that average crustal thickness could be down to 50 ± 12 km.[35]
Measurement of gravity field by different orbiters allows higher-resolution global Bouguer potential model to be produced.[5] With local shallow density anomalies and effect of core flattening eliminated,[5] the residual Bouguer potential is produced, as indicated by the following equation:
[5]
The residual Bouguer potential is contributed by the mantle.[5] The undulation of the crust-mantle boundary, or the Moho surface, with mass of terrain corrected, should have resulted in varying residual anomaly.[5] In turn, if undulating boundary is observed, there should be changes in crustal thickness.
Global study of residual Bouguer anomaly data indicates that crustal thickness of Mars varies from 5.8 km to 102 km.[5] Two major peaks at 32 km and 58 km are identified from an equal-area histogram of crustal thickness.[5] These two peaks are linked to the crustal dichotomy of Mars.[5] Almost all the crust thicker than 60 km are contributed by the southern highland, with generally uniform thickness.[5] And the northern lowland in general has thinner crust. The crustal thickness of the Arabia Terra region and northern hemisphere are found to be latitude-dependent.[5] The more southward towards the Sinai Planum and Lunae Planum, the more thickened the crust is.[5]
Among all regions, the Thaumasia and Claritis contain the thickest portion of crust on Mars that account for the histogram > 70 km.[5] The Hellas and Argyre basins are observed to have crust thinner than 30 km,[5] which are the exceptionally thin area in the southern hemisphere.[5] Isidis and Utopia are also observed to have significant crustal thinning,[5] with the center of Isidis basins believed to have the thinnest crust on Mars.[5]
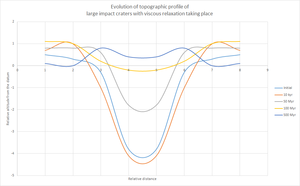
Crust redistribution by impacting and viscous relaxation[edit]
After the initial impact, high heat flux and high water content would have favored viscous relaxation to take place. The crust becomes more ductile. The basin topography of the craters is thus subjected to greater stress due to self-gravitation, which further drive crustal flow and decay of relief. However, this analysis may not work for giant impact craters such as Hellas, Utopia, Argyre and Isidis basins.[25]
Crustal thinning is believed to have taken place underneath almost all the major impact craters.[5] Crustal excavation, modification through emplacement of volcanic material and crustal flow taking place in the weak lithosphere are the possible causes.[5] With the pre-impact crust excavated, gravitational restoration would take place through central mantle uplift, so that the mass deficit of cavity could be compensated by the mass of the uplifted denser material.[5]
Giant impact basins Utopia, Hellas, Argyre and Isidis are some of the most prominent examples.[5] Utopia, an impact basin located in northern lowland, is filled by light and water-deposited sedimentary material and has slightly thickened crust at the center.[5] This is potentially due to large resurfacing process in the northern lowland.[5] While for Hellas, Argyre and Isidis basins, they have great Moho uplifted relief and exhibit annuli of diffuse thickened crust beyond the crustal rim.[5]
But on the contrary, almost all the Martian basins with diameter of 275 km < D < 1000 km are associated with low amplitude surface and low amplitude Moho relief.[25] Many are even found to have negative free air gravity anomaly, though evidence has shown that all of them should have experienced gravity high (positive free air gravity anomaly).[25] These have been suggested not caused by erosion and burial alone, as the adding of material into the basin would in fact increase the gravity strength rather than decrease it.[25] Thus viscous relaxation should have been taking place.[25] High heat flux and high water content in the early Martian crust favored viscous relaxation.[25] These two factors have made the crust more ductile. The basin topography of the craters would be subjected to greater stress due to self-gravitation. Such stress would drive crustal flow and therefore decay of relief. The giant impact basins are the exceptions that have not experienced viscous relaxation, as crustal thinning has made the crust too thin to sustain sub-solidus crustal flow.[5][25]
Low bulk crustal density[edit]
The most recent crustal density model RM1 developed in 2017 gives the bulk crustal density to be 2582 ± 209 kg m−3 for Mars,[9] which represents a global average value.[9] Lateral variation of the crustal density should exist.[9] For example, over the volcanic complexes, local density is expected to be as high as 3231 ± 95 kg m−3,[9] which matched the meteorite data and previous estimations. In addition, the density of the northern hemisphere is in general higher than that of the southern hemisphere,[9] which may imply that the latter is more porous than the former.
To achieve the bulk value, porosity could play an important role. If the mineral grain density is chosen to be 3100 kg m−3,[9] 10% to 23% porosity could give a 200 kg m−3 drop in the bulk density.[9] If the pore spaces are filled with water or ice, bulk density decrease is also expected.[9] A further drop in bulk density could be explained by increasing density with depth,[9] with the surface layer more porous than the deeper Mars, and the increase of density with depth also has geographical variation.[9]
Engineering and scientific applications[edit]
Areoid[edit]
The areoid is a planetary geoid that represents the gravitational and rotational equipotential figure of Mars, analogous to the concept of geoid («sea level») on Earth.[5][36][37] This has been set as the reference frame for developing the MOLA Mission Experiment Gridded Data Records (MEGDRs),[5][36] which is a global topography model. The topography model is important in mapping the geomorphological features and understanding different kinds of processes on Mars.
To derive the areoid, two parts of works are required. First, as gravity data is essential for identifying the position of the center of mass of the planet,[36] which is largely affected by the distribution of the mass of the interior, radio tracking data of spacecraft is necessary.[36] This was largely done by the Mars Global Surveyor (MGS).[5][36] Then, the MOLA 2 instrument aboard the MGS, which operates at 400-km elevation orbit, could measure the range (distance) between the spacecraft and the ground surface through counting the round-trip time of flight of the pulse from the instrument.[36] Combination of these two works allows the areoid as well as the MEGDRs to be constructed.
Based on the above, the areoid has taken the radius as the mean radius of the planet at the equator as 3396 km.[5][36]
The topography model MEDGRs was developed through range (distance) measurement done by MOLA 2 instrument and radio tracking data of the Mars Global Surveyor (MGS).[36] The highest point is located at the Olympus Mons while the deepest point is located within the Hellas Basin.[36](Brown-Red: Topography high; Green-Blue: Topography low) (Credit: NASA/JPL-Caltech)
Surface landing[edit]
As there is a large distance between Mars and Earth, immediate command to the lander is almost impossible and the landing relies highly on its autonomous system. It has been recognized that to avoid failure, precise understanding of the gravity field of Mars is essential for the landing projects, so that offsetting factors and uncertainties of gravitational effects could be minimized, allowing for a smooth landing progress.[38][39] The first ever man-made object landing on Mars, the Mars 2 lander, crashed for an unknown reason. Since the surface environment of Mars is complex, composed of laterally varying morphological patterns, in order to avoid rock hazard the landing progress should be further assisted by employment of LIDAR on site in determining the exact landing position and other protective measures.[38][39]
References[edit]
- ^ a b c d Hirt, C.; Claessens, S.J.; Kuhn, M.; Featherstone, W.E. (2012). «Kilometer-resolution gravity field of Mars: MGM2011». Planetary and Space Science. 67 (1): 147–154. Bibcode:2012P&SS…67..147H. doi:10.1016/j.pss.2012.02.006. hdl:20.500.11937/32270.
- ^ a b c d Watts, A. B.; Bodine, J. H.; Ribe, N. M. (1980-02-07). «Observations of flexure and the geological evolution of the Pacific Ocean basin». Nature. 283 (5747): 532–537. Bibcode:1980Natur.283..532W. doi:10.1038/283532a0. ISSN 1476-4687. S2CID 4333255.
- ^ a b c d e f g Jeffreys, H. (1959). The Earth 4th ed., 420.
- ^ a b c d e f Runcorn, S. K. (1965). «Changes in the Convection Pattern in the Earth’s Mantle and Continental Drift: Evidence for a Cold Origin of the Earth». Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 258 (1088): 228–251. Bibcode:1965RSPTA.258..228R. doi:10.1098/rsta.1965.0037. JSTOR 73348. S2CID 122307704.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as Neumann, G. A.; Zuber, M. T.; Wieczorek, M. A.; McGovern, P. J.; Lemoine, F. G.; Smith, D. E. (2004-08-01). «Crustal structure of Mars from gravity and topography» (PDF). Journal of Geophysical Research: Planets. 109 (E8): E08002. Bibcode:2004JGRE..109.8002N. doi:10.1029/2004je002262. ISSN 2156-2202.
- ^ a b c d Kiefer, Walter S. (2004-05-30). «Gravity evidence for an extinct magma chamber beneath Syrtis Major, Mars: a look at the magmatic plumbing system». Earth and Planetary Science Letters. 222 (2): 349–361. Bibcode:2004E&PSL.222..349K. doi:10.1016/j.epsl.2004.03.009.
- ^ a b c d e Marty, J.C.; Balmino, G.; Duron, J.; Rosenblatt, P.; Maistre, S. Le; Rivoldini, A.; Dehant, V.; Hoolst, T. Van (2009). «Martian gravity field model and its time variations from MGS and Odyssey data». Planetary and Space Science. 57 (3): 350–363. Bibcode:2009P&SS…57..350M. doi:10.1016/j.pss.2009.01.004.
- ^ a b c d e f g h i j Smith, David E.; Zuber, Maria T.; Torrence, Mark H.; Dunn, Peter J.; Neumann, Gregory A.; Lemoine, Frank G.; Fricke, Susan K. (2009-05-01). «Time variations of Mars’ gravitational field and seasonal changes in the masses of the polar ice caps». Journal of Geophysical Research: Planets. 114 (E5): E05002. Bibcode:2009JGRE..114.5002S. doi:10.1029/2008je003267. hdl:1721.1/74244. ISSN 2156-2202.
- ^ a b c d e f g h i j k l Goossens, Sander; Sabaka, Terence J.; Genova, Antonio; Mazarico, Erwan; Nicholas, Joseph B.; Neumann, Gregory A. (2017-08-16). «Evidence for a low bulk crustal density for Mars from gravity and topography». Geophysical Research Letters. 44 (15): 7686–7694. Bibcode:2017GeoRL..44.7686G. doi:10.1002/2017gl074172. ISSN 1944-8007. PMC 5619241. PMID 28966411.
- ^ «CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. Retrieved 2017-12-14. «2014 CODATA recommended values»
- ^ Jacobson, R. A. (2008). Ephemerides of the Martian Satellites—MAR080. JPL IOM 343R–08–006.
- ^ a b c d e Kaula, W. M. (1966-11-15). «Tests and combination of satellite determinations of the gravity field with gravimetry». Journal of Geophysical Research. 71 (22): 5303–5314. Bibcode:1966JGR….71.5303K. doi:10.1029/JZ071i022p05303. ISSN 2156-2202.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al Genova, Antonio; Goossens, Sander; Lemoine, Frank G.; Mazarico, Erwan; Neumann, Gregory A.; Smith, David E.; Zuber, Maria T. (2016). «Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science». Icarus. 272: 228–245. Bibcode:2016Icar..272..228G. doi:10.1016/j.icarus.2016.02.050.
- ^ a b c d e f Lemoine, F. G.; Smith, D. E.; Rowlands, D. D.; Zuber, M. T.; Neumann, G. A.; Chinn, D. S.; Pavlis, D. E. (2001-10-25). «An improved solution of the gravity field of Mars (GMM-2B) from Mars Global Surveyor». Journal of Geophysical Research: Planets. 106 (E10): 23359–23376. Bibcode:2001JGR…10623359L. doi:10.1029/2000je001426. ISSN 2156-2202.
- ^ a b Sinclair, A. T. (1971-12-01). «The Motions of the Satellites of Mars». Monthly Notices of the Royal Astronomical Society. 155 (2): 249–274. Bibcode:1971MNRAS.155..249S. doi:10.1093/mnras/155.2.249. ISSN 0035-8711.
- ^ a b c d Asmar, S. W.; Armstrong, J. W.; Iess, L.; Tortora, P. (2005-04-01). «Spacecraft Doppler tracking: Noise budget and accuracy achievable in precision radio science observations». Radio Science. 40 (2): RS2001. Bibcode:2005RaSc…40.2001A. doi:10.1029/2004RS003101. ISSN 1944-799X.
- ^ Mayor, Michel; Queloz, Didier (1995-11-23). «A Jupiter-mass companion to a solar-type star». Nature. 378 (6555): 355–359. Bibcode:1995Natur.378..355M. doi:10.1038/378355a0. ISSN 1476-4687. S2CID 4339201.
- ^ a b c Gapcynski, J. P.; Tolson, R. H.; Michael, W. H. (1977-09-30). «Mars gravity field: Combined Viking and Mariner 9 results». Journal of Geophysical Research. 82 (28): 4325–4327. Bibcode:1977JGR….82.4325G. doi:10.1029/js082i028p04325. ISSN 2156-2202.
- ^ a b c d Balmino, G.; Moynot, B.; Valès, N. (1982-01-01). «Gravity field model of mars in spherical harmonics up to degree and order eighteen». Journal of Geophysical Research: Solid Earth. 87 (B12): 9735–9746. Bibcode:1982JGR….87.9735B. doi:10.1029/jb087ib12p09735. ISSN 2156-2202.
- ^ a b c d Smith, D. E.; Lerch, F. J.; Nerem, R. S.; Zuber, M. T.; Patel, G. B.; Fricke, S. K.; Lemoine, F. G. (1993-11-25). «An improved gravity model for Mars: Goddard Mars model 1». Journal of Geophysical Research: Planets. 98 (E11): 20871–20889. Bibcode:1993JGR….9820871S. doi:10.1029/93JE01839. ISSN 2156-2202.
- ^ a b c Konopliv, Alexander S; Sjogren, William L (February 1, 1995). «The JPL Mars gravity field, Mars50c, based upon Viking and Mariner 9 Doppler tracking data». NASA Sti/Recon Technical Report N. 95: 30344. Bibcode:1995STIN…9530344K – via NASA Technical Report Server.
- ^ a b c Lemoine, F. G., 2009. NASA PDS. http://pdf-geosciences.wustl.edu/mro/mro-m-rss-5-sdp-v1/mrors_1xxx/data/shadr/ggmro_095a_sha.lbl.
- ^ a b c Konopliv, Alex S.; Yoder, Charles F.; Standish, E. Myles; Yuan, Dah-Ning; Sjogren, William L. (2006). «A global solution for the Mars static and seasonal gravity, Mars orientation, Phobos and Deimos masses, and Mars ephemeris». Icarus. 182 (1): 23–50. Bibcode:2006Icar..182…23K. doi:10.1016/j.icarus.2005.12.025.
- ^ a b c d Konopliv, Alex S.; Asmar, Sami W.; Folkner, William M.; Karatekin, Özgür; Nunes, Daniel C.; Smrekar, Suzanne E.; Yoder, Charles F.; Zuber, Maria T. (2011). «Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters». Icarus. 211 (1): 401–428. Bibcode:2011Icar..211..401K. doi:10.1016/j.icarus.2010.10.004.
- ^ a b c d e f g h i Mohit, P. Surdas; Phillips, Roger J. (2007-11-01). «Viscous relaxation on early Mars: A study of ancient impact basins». Geophysical Research Letters. 34 (21): L21204. Bibcode:2007GeoRL..3421204M. doi:10.1029/2007GL031252. ISSN 1944-8007.
- ^ a b Airy, G. B. (1855). «On the Computation of the Effect of the Attraction of Mountain-Masses, as Disturbing the Apparent Astronomical Latitude of Stations in Geodetic Surveys». Philosophical Transactions of the Royal Society of London. 145: 101–104. doi:10.1098/rstl.1855.0003. JSTOR 108511. S2CID 186210268.
- ^ a b c Beuthe, M.; Le Maistre, S.; Rosenblatt, P.; Pätzold, M.; Dehant, V. (2012-04-01). «Density and lithospheric thickness of the Tharsis Province from MEX MaRS and MRO gravity data». Journal of Geophysical Research: Planets. 117 (E4): E04002. Bibcode:2012JGRE..117.4002B. doi:10.1029/2011je003976. ISSN 2156-2202.
- ^ Runcorn, S. K. (1963). «Satellite gravity measurements and convection in the mantle». Nature. 200 (4907): 628–630. Bibcode:1963Natur.200..628R. doi:10.1038/200628a0. S2CID 4217054.
- ^ A B Watts; Daly, and S. F. (1981). «Long Wavelength Gravity and Topography Anomalies». Annual Review of Earth and Planetary Sciences. 9 (1): 415–448. Bibcode:1981AREPS…9..415W. doi:10.1146/annurev.ea.09.050181.002215.
- ^ McKenzie, Dan (1977-02-01). «Surface deformation, gravity anomalies and convection». Geophysical Journal of the Royal Astronomical Society. 48 (2): 211–238. Bibcode:1977GeoJ…48..211M. doi:10.1111/j.1365-246X.1977.tb01297.x. ISSN 1365-246X.
- ^ a b c Yoder, C. F.; Konopliv, A. S.; Yuan, D. N.; Standish, E. M.; Folkner, W. M. (2003-04-11). «Fluid Core Size of Mars from Detection of the Solar Tide». Science. 300 (5617): 299–303. Bibcode:2003Sci…300..299Y. CiteSeerX 10.1.1.473.6377. doi:10.1126/science.1079645. ISSN 0036-8075. PMID 12624177. S2CID 23637169.
- ^ a b c Karatekin, Ö.; Van Hoolst, T.; Dehant, V. (2006-06-01). «Martian global-scale CO2 exchange from time-variable gravity measurements». Journal of Geophysical Research: Planets. 111 (E6): E06003. Bibcode:2006JGRE..111.6003K. doi:10.1029/2005je002591. ISSN 2156-2202.
- ^ Sohl, Frank; Spohn, Tilman (1997-01-25). «The interior structure of Mars: Implications from SNC meteorites». Journal of Geophysical Research: Planets. 102 (E1): 1613–1635. Bibcode:1997JGR…102.1613S. CiteSeerX 10.1.1.456.2309. doi:10.1029/96JE03419. ISSN 2156-2202.
- ^ Nimmo, F.; Stevenson, D. J. (2001-03-25). «Estimates of Martian crustal thickness from viscous relaxation of topography» (PDF). Journal of Geophysical Research: Planets. 106 (E3): 5085–5098. Bibcode:2001JGR…106.5085N. doi:10.1029/2000JE001331. ISSN 2156-2202.
- ^ Wieczorek, Mark A.; Zuber, Maria T. (2004-01-01). «Thickness of the Martian crust: Improved constraints from geoid-to-topography ratios». Journal of Geophysical Research: Planets. 109 (E1): E01009. Bibcode:2004JGRE..109.1009W. doi:10.1029/2003JE002153. ISSN 2156-2202.
- ^ a b c d e f g h i Smith, David E.; Zuber, Maria T.; Frey, Herbert V.; Garvin, James B.; Head, James W.; Muhleman, Duane O.; Pettengill, Gordon H.; Phillips, Roger J.; Solomon, Sean C. (2001-10-25). «Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars» (PDF). Journal of Geophysical Research: Planets. 106 (E10): 23689–23722. Bibcode:2001JGR…10623689S. doi:10.1029/2000je001364. ISSN 2156-2202.
- ^ Ardalan, A. A.; Karimi, R.; Grafarend, E. W. (2009). «A New Reference Equipotential Surface, and Reference Ellipsoid for the Planet Mars». Earth, Moon, and Planets. 106 (1): 1–13. doi:10.1007/s11038-009-9342-7. ISSN 0167-9295. S2CID 119952798.
- ^ a b Balaram, J., Austin, R., Banerjee, P., Bentley, T., Henriquez, D., Martin, B., … & Sohl, G. (2002). Dsends-a high-fidelity dynamics and spacecraft simulator for entry, descent and surface landing. In Aerospace Conference Proceedings, 2002. IEEE (Vol. 7, pp. 7–7). IEEE.
- ^ a b Braun, R. D.; Manning, R. M. (2007). «Mars Exploration Entry, Descent, and Landing Challenges». Journal of Spacecraft and Rockets. 44 (2): 310–323. Bibcode:2007JSpRo..44..310B. CiteSeerX 10.1.1.463.8773. doi:10.2514/1.25116.
Каждый из нас когда-либо задумывался о жизни вне Земли, однако не каждый знает о том, какую роль в жизнеспособности тела играет его магнитное поле. Гипотеза ученых о том, что жизнь на Марсе возможна, имеет веские основания. Какие для этого необходимы условия, и какую роль в жизнеобеспечении играет магнитное поле, читаем ниже.
Магнитное поле Марса
Магнитное поле представляет собой некую защитную оболочку, отклоняющую все негативные воздействия ветра, электрических зарядов Солнца или других планет. Такое защитное поле имеет не каждая планета, оно продуцируется внутренними тепловыми и динамическими процессами, происходящими центре ядра космического тела. Частицы расплавленного металла, находясь в движении, создают электроток, наличие которого на планете участвует в создании защитного слоя.
Магнитное поле Марса однозначно существует, оно распределено очень слабо и неравномерно. Это объясняется неподвижностью остывшего ядра относительно поверхности. На планете есть места, где проявление поля в несколько раз превышает силу воздействия на других участках четвертой планеты. Магнитометром Mars Global Surveyor было установлено наличие наиболее сильного магнитного поля на южных участках, в то время как на северной стороне оно прибором практически не было установлено.
Магнитное поле у Марса ранее было достаточно сильным, оно имеет остаточный характер, сохраняя так называемый палеомагнетизм. Этого поля недостаточно для защиты от излучений Солнца или воздействия ветров. Таким образом, незащищенная поверхность не оставляет возможности задерживаться ни воде, ни другим частицам.
На вопрос было ли магнитное поле у Марса, и есть ли оно сейчас, можно уверенно дать положительный ответ. Наличие небольшого поля на соседней планете говорит о том, что оно существовало и ранее, имея большую, нежели сегодня силу.
Почему Марс потерял магнитное поле
Есть теория, согласно которой еще 4 млрд. лет назад магнитное поле красной планеты было достаточно сильным. Оно было схоже с земным и стабильно распределялось на поверхности его коры.
Столкновение с неким космическим телом больших размеров, или, как утверждают некоторые исследователи, несколькими крупными астероидами, повлияло на внутренние динамические процессы ядра. Ядро перестало продуцировать электротоки, вследствие чего, поле Марса ослабло, его распределение стало неоднородным: оно стало усилено на одних участках, другие остаются незащищенными. В этих местах воздействие излучения Солнца в два с половиной раза сильнее, чем на Земле.
Насколько сильна гравитация на Марсе?
В силу слабого и неравномерно распределенного магнитного поля, гравитация на Марсе имеет столь же низкие параметры. Если быть точнее, сравнительно с земной силой притяжения, она на 62% слабее. Поэтому все субъекты, находящиеся здесь в разы теряют свою истинную массу.
Сила притяжения на Марсе зависит от нескольких параметров: массы, радиуса, а также плотности. Несмотря на то, что площадь Марса приближается к показателям площади Земли, существуют большие различия плотности и диаметров планет, масса Марса на 89% меньше земной.
Имея данные двух схожих планет, учеными была вычислена сила притяжения Марса, которая достаточно отличается от земной. Сила гравитации на Марсе так же ослаблена, как и магнитное поле. Низкая гравитация перестраивает работу живого существа. Поэтому длительное пребывание человека на Красной плане может негативным образом сказаться на здоровье. Если будет найден путь преодоления последствий слабого притяжения на здоровье человека, время освоения других планет стремительно приблизится.
Помимо силы тяготения, на самой планете существует величина – гравитационная постоянная, показывает силу тяготения между планетами. Она вычисляется относительно двух планет, Марса и Земли, Марса и Солнца отдельно с учетом расстояния между ними. Эта величина является основополагающей, так как от силы тяготения планет зависит и расстояние между ними.
Расчет марсианской гравитации
Чтобы найти силу гравитации на Марсе, нужно применить формулу:
G = m(земли) • m(Марса) /r2
Здесь – это гравитационная постоянная, r – это расстояние от центров Земли и Марса.
Подставив значения, получим
5.97 • 1024 • 0.63345 • 6.67 • 10-11 /3.488=3.4738849055214
Таким образом, значение марсианской гравитации равно 3.4738849055214 Н.
Почему на Марсе по-другому
Сила тяжести Марса относительно Земли зависит от размера планет, массы и расстояния между их центрами. Планета с большей массой оказывает наибольшую степень гравитационного притяжения. Таким образом, Земля, имея наибольшую массу, оказывает наибольшую силу притяжения относительно Марса. По мере увеличения расстояния между планетами, сила гравитации между ними уменьшается.
Гравитация Земли, имея высокие показатели, способна с большей силой, нежели на Марсе притягивать объекты. Таким образом, земная гравитация, по сравнению с марсианской, позволяет сохранять жизнедеятельность и жизнеспособность на Земле. В то время как на Марсе низкая сила тяготения не удерживает на поверхности планеты даже воду.
Сравнительный анализ характера силы притяжения на Марсе относительно силы тяготения Земли, позволяет ответить на вопрос, почему на Марсе нет такого магнитного поля, как на Земле.
Несмотря на схожесть двух планет: площади, наличие полярных шапок, схожего наклона оси вращения и климатических изменений, Марс и Земля имеют весомые различия. Показатель давления на Марсе на 99 992.5 миллибар ниже давления на Земле. Сезонная температура Марса во много раз ниже, чем на Земле. Так, зимой был зарегистрирован минимальный показатель -143 градуса, летом поверхность разогревается до 35 градусов тепла.
Ученые заняты рассмотрением условий, при которых жизнь на четвертой от Солнца будет возможна. На данный момент исследований Красной планеты недостаточно, чтобы собрать данные жизни на Марсе, так как низкое магнитное поле и сила гравитации усложняют пребывание человека на планете, точнее подвергают его организм нежелательным изменениям, что вряд ли совместимо с жизнью.
Пригодилась информация? Плюсани в социалки!
- 30 Новейших, известных и спорных фактов о планете Марс
- Атмосфера Марса — химический состав, погодные условия и климат в прошлом
- Марс в разрезе: внутреннее строение, геологическая эволюция и состав
Гравитация Марса — это естественное явление из-за закона всемирного тяготения, или гравитация, с помощью которых все объекты с массой вокруг планеты Марс притягиваются к ней. Он слабее, чем земное притяжение из-за меньшей массы планеты. Среднее ускорение свободного падения на Марсе составляет 3,72076 мс (примерно 38% от земного ), и оно изменяется в поперечном направлении. В общем, контролируемая топографией изостазия вызывает коротковолновые аномалии силы тяжести в открытом воздухе . В то же время конвективный поток и конечная прочность мантии приводят к длинноволновым гравитационным аномалиям в воздухе планетарного масштаба над всей планетой. Изменение толщины земной коры, магматическая и вулканическая деятельность, вызванный ударом Мохо -подъем, сезонные колебания полярных ледяных шапок, изменение массы атмосферы и изменение пористости коры также могут быть связаны с боковыми вариациями. За прошедшие годы были произведены модели, состоящие из увеличивающегося, но ограниченного числа сферических гармоник. Созданные карты включают аномалию силы тяжести в открытом воздухе, аномалию силы тяжести Бугера и толщину земной коры. В некоторых областях Марса существует корреляция между гравитационными аномалиями и топографией. Учитывая известную топографию, можно сделать вывод о гравитационном поле с более высоким разрешением. Приливную деформацию Марса Солнцем или Фобосом можно измерить по его гравитации. Это показывает, насколько жестка внутренняя часть, и показывает, что ядро частично жидкое. Таким образом, изучением поверхностной гравитации Марса может дать информацию о различных особенностях и предоставить полезную информацию для будущих проектов посадки.
Содержание
- 1 Измерение
- 1.1 Наблюдения с Земли
- 1.2 На основе данных радиосопровождения
- 2 История
- 3 Статическое гравитационное поле
- 3.1 Локальные гравитационные аномалии
- 3.1. 1 Аномалии топографии
- 3.1.2 Аномалии от вулканических построек
- 3.1.3 Аномалии от депрессий
- 3.2 Глобальные гравитационные аномалии
- 3.1 Локальные гравитационные аномалии
- 4 Гравитационное поле, изменяющееся во времени
- 4.1 Сезонное изменение гравитационного поля на полюсах
- 5 Прилив
- 6 Геофизические последствия
- 6.1 Толщина земной коры
- 6.2 Перераспределение коры за счет ударной и вязкой релаксации
- 6.3 Низкая объемная плотность земной коры
- 7 Технические и научные приложения
- 7.1 Ареоид
- 7.2 Посадка на поверхность
- 8 Справочная информация
Измерение

l { displaystyle l}

м { displaystyle m}

Чтобы понять гравитацию Марса, часто измеряют его напряженность гравитационного поля g и гравитационный потенциал U. Проще говоря, если предположить, что Марс является статическим идеально сферическим телом радиусом R M, при
GM mr 2 = mr ω 2 { displaystyle { frac {GMm}), что есть только один спутник, вращающийся вокруг Марса по круговой орбите, и такое гравитационное взаимодействие является единственной силой, действующей в системе, уравнение будет вид
{r ^ {2}}} = mr omega ^ {2}}
где G — универсальная гравитационная постоянная (обычно принимаемая как G = 6,674 x 10 м кг · с), M — масса Марса (наиболее актуальное значение: 6,41693 x 10 кг), m — масса спутника, r — расстояние между Марсом и спутником, а ω { displaystyle omega}

Следовательно, g = GMRM 2 = r 3 ω 2 RM 2 = 4 r 3 π 2 T 2 RM 2 { displaystyle g = { frac {GM} {R_ {M} ^ { 2}}} = { frac {r ^ {3} omega ^ {2}} {R_ {M} ^ {2}}} = { frac {4r ^ {3} pi ^ {2}} { T ^ {2} R_ {M} ^ {2}}}}
Однако, поскольку Марс является обычным несферическим планетным телом и находится под сложными геологическими процессами, гравитационный потенциал точно описывается с помощью сферических гармонических функций, следуя соглашению в геодезии, см. Геопотенциальная_модель.
U (r, λ, ψ) = — GM r (1 + ∑ l = 2 l = L (R r) l (C l 0 P l 0 (sin ψ) + ∑ ì знак равно 1 + l (C лм соз м λ + S лм грех м λ) п лм ( ψ))) { displaystyle U (r, lambda, psi) = — { frac {GM} { r}} left (1+ textstyle sum _ {l = 2} ^ {l = L} displaystyle left ({ frac {R} {r}} right) ^ {l} left (C_ {l0} P_ {l} ^ {0} ( sin psi) + sum _ {m = 1} ^ {+ l} (C_ {lm} cos m lambda + S_ {lm} sin m lambda) P_ {l} ^ {m} ( sin psi) right) right)}
где r, ψ, λ { displaystyle r, psi, lambda}













- Меньшая степень l { displaystyle l}
и порядок m { displaystyle m}
, чем большую длину волны аномалии он представляет. гравитационная аномалия находится под глобальных геофизических структур.
- Чем выше степень l { displaystyle l}
и порядок m { displaystyle m}
, чем короче длина волны аномалии, которую он представляет. Для степени выше 50 было показано, что эти вариации имеют корреляцию с топографией. Геофизическая интерпретация поверхности могла бы помочь получить более полную картину гравитационного поля Марса, хотя могут быть получены вводящие в заблуждение результаты.
Самый старый метод определения силы тяжести Марса — это наблюдение с Земли. Позже, с появлением беспилотных космических аппаратов, на основе данных радиотрекинга были разработаны последующие гравитационные модели.

Наблюдения с Земли
Перед прибытием Mariner 9 и Орбитальный аппарат «Викинг» на Марсе, только оценка постоянной марсианской гравитационной GM, то есть универсальная гравитационная постоянная, умноженная на массу Марса, доступная для вывода свойств марси гравитации. поле. GM может быть получен посредством наблюдений за движением естественных спутников Марса (Фобос и Деймос ) и пролетов космических кораблей Марса (Mariner 4 и Mariner 6 ).
Долгосрочные наземные наблюдения за движением Фобоса и Деймоса позволяют получить физические параметры, включая большую полуось, эксцентриситет, угол наклона к лапласианской плоскости и т. Д., Которые позволяют вычислить отношение массы Солнца к массе Марса, момента инерции, и коэффициента гравитационного потенциала Марса, а также дают начальные оценки гравитационного поля Марса.
На основе данных радиослежения
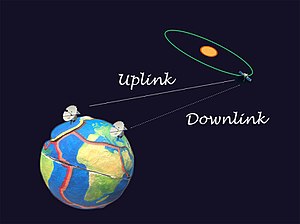
Точное отслеживание космического корабля имеет первостепенное значение для моделирования гравитации, поскольку гравитационные модели разрабатываются на основе наблюдения крошечных возмущений космического корабля, то есть небольшое изме. нение скорости и высоты. Отслеживание осуществляется в основном с помощью антенны отсутствует в сети Deep Space Network (DSN), с применением одностороннего, двустороннего и трехстороннего доплеровского режима и системы дальности. Одностороннее слежение означает, что данные передаются односторонним образом в DSN с космического корабля, в то время как двустороннее и трехстороннее включает передачу сигналов с Земли на космический корабль (восходящая линия связи), а когерентно ретранслируются обратно на Землю (нисходящая линия связи).. Разница между двухсторонним и трехсторонним слежением состоит в том, что у первого из них один и тот же передатчик и приемник сигнала на Земле, а у второго — передатчик и приемник в разных местах на Земле. Использование трех типов данных слежения увеличивает количество данных, поскольку один может заполнить пробел в данных другого.
Доплеровское слежение — это распространенный метод слежения за космическим кораблем с использованием метода радиальной скорости, включает обнаружение доплеровских сдвигов. По мере того, как космический корабль удаляется от нас по линии видимости, сигнал будет смещаться в красную область, а в обратном направлении — в синюю. Такой метод также применяется для наблюдения за движением экзопланет. Выполните измерение времени распространения сигнала туда и обратно. Комбинация доплеровского сдвига и наблюдения за дальностью обеспечивает высокую точность установки космического корабля.
Также данные будут преобразованы для разработки глобальных гравитационных моделей с использованием уравнения сферической гармоники, показанного выше. Однако дальнейшее устранение эффектов из-за воздействия твердого прилива, различных релятивистских эффектов из-за воздействия Солнца, Юпитера и Сатурна, неконсервативных сил (например, (AMD), атмосферное сопротивление и давление солнечного излучения ), возникают данные ошибки.
История
Последней гравитационной модели для Марса модель Годдарда Марса 3 (GMM-3), выпущенная в 2016 году, с решением сферических гармоник до степени и порядка 120. Эта модель добавлена на основе данных радиослежения за 16 лет, полученные от Mars Global Surveyor (MGS), Mars Odyssey и Mars Reconnaissance Orbiter (MRO), а также топографической модели MOLA и обеспечивает глобальное разрешение 115 км. Вместе с этой моделью были созданы отдельная карта гравитационных аномалий в свободном воздухе, карта гравитационных аномалий Бугера и карта толщины земной коры. По сравнению с MRO110C и другими предыдущими моделями, значительное улучшение оценки гравитационного поля происходит благодаря более тщательному моделированию неконсервативных сил, действующих на космический корабль.
| Гравитационные решения | Авторы | Год | Степень (м) и порядок (l) решения сферической гармоники
[Разрешение поверхности (км)] |
Источник данных |
|---|---|---|---|---|
| – | JP Gapcynski, RH Tolson и WH Michael Jr | 1977 | 6 | Данные слежения за космическими кораблями Mariner 9, Viking 1 и 2 |
| Geoide martien | Г. Балмино, Б. Мойнот и Н. Валес | 1982 | 18
[¬600 км] |
Данные слежения за космическими кораблями Mariner 9, Viking 1 и 2 |
| GMM-1 | DE Smith, FJ Lerch, RS Нерем, М.Т. Зубер, Г.Б. Патель, С.К. Фрике и Ф.Г. Лемуан | 1993 | 50
[200–300 км] |
Данные слежения за космическими кораблями Mariner 9, Viking 1 и 2 |
| Mars50c | А.С. Коноплив, В.Л. Шегрен | 1995 | 50 | Данные слежения за космическими кораблями Mariner 9, Viking 1 и 2 |
| GMM-2B | FG Lemoine, DE Smith, DD Rowlands, MT Z uber, GA Neumann, DS Chinn и DE Pavlis | 2001 | 80 | Данные предоставлены Mars Global Surveyor (MGS) и данные топографии, полученные с помощью MOLA |
| GGM1041C | FG Lemoine | 2001 | 90 | Данные предоставлены Mars Global Surveyor (MGS) и Mars Odyssey, а также данные топографии, полученные из MOLA |
| MGS95J | AS Konopliv, CF Yoder, EM Standish, DN Yuan, WL Sjogren | 2006 | 95
[~ 112 км] |
Данные представлены Mars Global Surveyor (MGS) и Mars Odyssey, а также данные топографии, полученные с помощью MOLA |
| MGGM08A | JC Марти, Дж. Бальмино, Дж. Дюрон, П. Розенблатт, С. Ле Местр, А. Ривольдини, В. Дехан, Т. Ван Хулст | 2009 | 95
[~ 112 км] |
Данные данныео Mars Global Surveyor (MGS) и Mars Odyssey, а также данные топографии, полученные с помощью MOLA |
| MRO110B2 | А.С. Коноплив, С.В. Асмар, В.М. Фолкнер, Ö Каратекин, Д.К. Нунес, С.Е. Смрекар, К.Ф. Йодер, М.Т.>2011 | 110 | Данные предоставлены Mars Global Surveyor (MGS), Mars Odyssey и Mars Reconnaissance Orbiter), а также MOLA-der Полученные данные топографии | |
| MGM2011 | C Hirt, SJ Claessens, M. Kuhn, WE Featherstone | 2012 | [3 км (экватор) — 125 км] | Гравитационное решение MRO110B2 и данные топографии на На основе MOLA |
| GMM-3 | A Genova, S. Goossens, FG Lemoine, E. Mazarico, GA Neumann, DE Smith, MT Zuber | 2016 | 120
[115 км] |
Mars Global Surveyor (MGS), Mars Odyssey и Mars Reconnaissance Orbiter (MRO)
|
Методы слежения за космическим кораблем и геофизическая интерпретация поверхности влиять на разрешение сила гравитационного поля. Лучшая методика отдает предпочтение сферическим гармоническим решениям более высоких степеней и порядков. Независимый анализ данных слежения за Mariner 9 и Viking Orbiter далекое решение по сферической гармонике степени и порядка 6. Дальнейшее объединение двух наборов данных вместе с корреляцией аномалий с вулканическими особенностями (положительная аномалия) отпечатанная впадина (отрицательная аномалия) с помощью данных изображения позволяет получить решение со степенью и порядком 18 сферических гармоник. Дальнейшее использование метода пространственных априорных ограничений, учитывающего топографию при решении степенного закона Каулы, привело к модели решения сферической гармоники до 50 степени с глобальным разрешением (или GMM-1), а последующим моделям с более высокой полнота и степень и порядок до 120 для последней модели GMM-3.

Таким образом, в настоящее гравитационные модели не представляют Посредством передачи данных гравитационных данных в какую-либо пространственную информационную систему. Данные топографии, полученные с помощью прибора MOLA на борту Mars Global Surveyor, таким образом, получены инструменты для создания более подробной мелкомасштабной гравитационной модели с использованием корреляции гравитационной топографии в коротковолновой области.. Однако не все регионы Марса демонстрируют такую корреляцию, особенно северная низменность и полюса. Можно легко получить вводящие в заблуждение результаты, которые могут привести к неправильной геофизической интерпретации.
Более поздние модификации гравитационной модели, включая сопротивление атмосферы, давление солнечного излучения, отраженное Марсом давление солнечного излучения, тепловое излучение Марса и толчок космического корабля, который ослабляет или обесцвечивает. Кроме того, марсианская прецессия и притяжение третьего тела из-за Солнца, Луны и планет, которые могут повлиять на орбиту космического корабля, а также на измерениях тоже надо поправить. Эти факторы могут привести к смещению истинного гравитационного поля. Таким образом, для устранения ущерба требуется точное моделирование. Такая работа все еще продолжается.
Статическое гравитационное поле
Многие исследователи отметили корреляцию между коротковолновыми (локально изменяемыми) гравитационными аномалиями в свободном воздухе и топографией. Для регионов с более высокой степенью аномалии силы тяжести в более высокой степени могут быть расширены до более высокой степени за счет геофизической интерпретации поверхностных элементов. Было обнаружено, что южное нагорье имеет силу тяжести / топографии, но не северную низменность. Следовательно, разрешение модели аномалии силы тяжести в свободном воздухе обычно имеет более высокое разрешение для южного полушария, достигающее более 100 км.
Аномалии силы тяжести в свободном воздухе легче измерить, чем аномалии Бугера. при условии, что данные топографии доступны, потому что не требуется устранять гравитационный эффект из-за эффекта избытка массы или дефицита местности после того, как сила тяжести снижается до уровня моря. Чтобы интерпретировать изменение положения земной коры, необходимо дальнейшее устранение такого гравитационного эффекта, чтобы уменьшенная гравитация была результатом ядра, мантии и коры ниже точки отсчета. Продукт после устранения — аномалии Буге. Однако плотность материала при построении местности будет наиболее ограниченным в расчетах, которое может изменяться по горизонтали на планете и зависит от пористости и геохимии породы. Соответствующая информация может быть получена из марсианских метеоритов и анализа на месте.
Локальные гравитационные аномалии
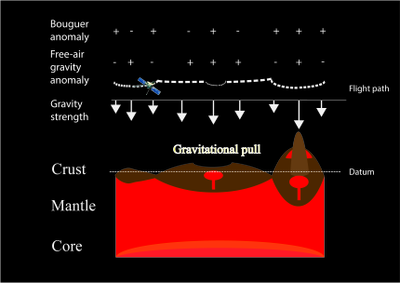
Поскольку гравитационные аномалии Буге имеют сильную связь с глубиной границы кора-мантия, одна с положительными аномалиями Буге может означать, что она имеет более тонкую кору, состоящую из материала с более низкой плотностью, и на нее сильнее влияет более плотная мантия., наоборот. Однако этому также может способствовать разница в плотности извергнутой вулканической нагрузки и осадочной нагрузки, а также подземное проникновение и удаление материала. Многие из этих аномалий связаны либо с геологическими, либо с топографическими особенностями. Немногие исключения включают аномалию 63 ° в.д., 71 ° с.ш., которая может представлять собой обширную погребенную структуру размером более 600 км, предшествовавшую раннему захоронению поверхности в эпоху Ноя.
Аномалии топографии
Сильные Корреляция между топографией и коротковолновыми гравитационными аномалиями в свободном воздухе была показана как при исследовании гравитационного поля Земли, так и Луны, и ее можно объяснить широким распространением изостазии. Высокая корреляция ожидается для степени выше 50 (коротковолновая аномалия) на Марсе. И оно может достигать 0,9 для градусов между 70 и 85. Такое соотношение можно объяснить компенсацией изгиба топографических нагрузок. Отмечено, что более старые области на Марсе изостатически компенсируются, тогда как более молодые области обычно компенсируются только частично.
Аномалии от вулканических построек

Различные вулканические конструкции могут вести себя по-разному с точки зрения гравитационных аномалий. Большие вулканы Olympus Mons и Tharsis Montes самые большие положительные аномалии силы тяжести в открытом воздухе в солнечной системе. Альба-Патера, также вулканическое поднятие, к северу от Тарсис Монтес, однако производит отрицательную аномалию Буге, хотя ее расширение аналогично таковой у Олимпа Монс. А для Элизиум Монс обнаружено, что в его центре наблюдается небольшое аномалий в общем целом отрицательных аномалий в подъеме Элизиума.
Знание об аномалии вулканов, наряду с плотностью вулканического материала, будет полезна для определения состава литосферы и эволюции земной коры различных вулканических построек. Было предположено предположение, что экструдированная лава может изменяться от андезита (низкая плотность) до базальта (высокая плотность), и состав может измениться во время строительства вулканического щита, что аномалия. Другой сценарий — это возможно для материала высокой плотности, проникшего под вулкан. Такая обстановка уже наблюдалась над знаменитым Syrtis major, который, как предполагалось, имел потухший магматический очаг глубиной 3300 кг м под вулканом, что очевидно из положительной аномалии Буге.
Аномалии от депрессии
Различные депрессии также по-разному ведут себя при аномалии Буге. Гигантские ударные бассейны, такие как бассейны Аргир, Исидис, Эллада и Утопия, также демонстрируют очень сильные положительные аномалии Буге в форме круга. Эти бассейны обсуждались из-за их происхождения от ударных кратеров. Если да, то положительные аномалии связаны с поднятием Мохо, утонением земной коры и модификациями из-за осадочных и вулканических поверхностных нагрузок после удара.
Но в то же время есть и некоторые крупные бассейны, которые не связаны с такой положительной аномалией Буге, например, Дедалия, северная Фарсида и Элизиум, которые, как полагают, подстилаются северной низменностью равниной.
Кроме того, на некоторых участках Coprates, Eos Chasma и Kasei Valles также обнаружены положительные аномалии Буге, хотя они представляют собой топографические депрессии. Это может свидетельствовать о том, что эти депрессии подстилаются неглубоким плотным теломжения.
Глобальные гравитационные аномалии
Глобальные гравитационные аномалии, также называемые волновыми гравитационными аномалиями, являются гармониками низкой степени гравитационного поля, которое не может быть объяснено локальной изостазией, а скорее конечной силой мантии и перепадами плотности конвективного течения. Для Марсашим индексом аномалии Бугера представляет собой гармоника первой степени, которая представляет собой дефицит массы в южном полушарии и превышток в северном полушарии. Второй по величине компонент соответствует выпуклости и Тарсис.
Ранние исследования геоида в 1950-х и 1960-х годах были сосредоточены на низкоуровневых гармониках гравита поля Земли, чтобы понять его внутреннюю структуру. Было высказано предположение, что такие длинноволновые аномалии на Земле могут быть вызваны источниками, расположенными в глубокой мантии, а не в коре, например, вызванными разницей плотности в движущем конвекционном токе, который развивается со временем. Корреляция между некоторыми аномалиями топографией и расширениями аномалиями силы тяжести, например, срединно-Атлантическим хребтом и хребтом Карлсберг, которые имеют повышенную гравитацию на территории океана, таким образом современные идеи конвекции на Земле в 1970-х годах, хотя такие корреляции слабы в глобальной картине.
Другим возможным объяснением аномалий глобального глобального мантийного (отличие от нулевого напряжения), которое вызывает отклонение силы тяжести от гидростатического равновесия. Согласно теории, из-за конечной прочности, поток может не существовать для большей части недонагруженных областей. Произошедшие химические неоднородности, связанные с разделением континентов, и шрамов, оставшихся на Земле после того, как Луна оторвалась. Это те случаи, которые, рекомендуются для работы, когда обстоятельства непредвиденный медленный поток. Однако утверждалось, что эта теория может быть физически невыполнимой.
Гравитационное поле, изменяющееся во время

Сезонное изменение гравитационного поля на полюсах
Цикл сублимация — конденсация углекислого газа на Марсе между атмосферой и криосферой (полярная ледяная шапка) работает сезонно. Этот цикл вносит свой вклад как почти единственная переменная, учитывающая изменения гравитационного поля на Марсе. Измеренный гравитационный потенциал Марса с орбитальных аппаратов можно обобщить следующим образом:
V (M ars) = V (S olidplanet) + V (S easonalcaps + Атмосфера) { displaystyle V (Mars) = V ({Solid , planet}) + V (Seasonal , caps + Atmosphere)}
В свою очередь, когда в сезонных ограничениях больше массы из-за большей конденсации углекислого газа из атмосферы, массы атмосферы будет падение. У них обратные отношения друг с другом. И изменение массы имеет прямое влияние на измеренный гравитационный потенциал.
Сезонный массообмен между северной полярной шапкой и южной полярной шапкой демонстрирует длинноволновое изменение силы тяжести со временем. Долгие непрерывных наблюдений показали, что определение четного зонального нормированного коэффициента гравитации C l = 2, m = 0 и нечетного зонального нормированного коэффициента гравитации C l = 3, m = 0 имеют решающее значение для определения изменяющейся во времени гравитации из-за такого массообмена, где l { displaystyle l}

Если мы рассматриваем два полюса как две точечные массы, то их массы определяют как,
MNP = C 20 + C 30 2 MM ars { displaystyle M_ {NP} = { frac {C_ { 20} + C_ {30}} {2}} , M_ {Mars}}
MSP = C 20 — C 30 2 мм арс { displaystyle M_ {SP} = { frac {C_ {20} -C_ {30}} {2}} , M_ {Марс}}
Показано, что максимальное изменение массы южной полярной шапки составляет примерно 8,4 x 10 кг, что около осеннего равноденствия, в то время как для северного полюса составляет примерно 6,2 x 10 кг, что происходит в период между зимним солнцестоянием и весенним равноденствием.
В долгосрочной перспективе было обнаружено, что масса льда, хранящегося на Северном полюсе, увеличится на (1,4 ± 0,5) x 10 кг, а на Южном полюсе — на (0,8 ± 0,6) x 10 кг. Кроме того, в долгосрочной перспективе масса углекислого газа в атмосфере уменьшится на (0,6 ± 0,6) х 10 кг. Из-за наличия неопределенностей неясно, продолжается миграция материала с Южного полюса на Северный, хотя такую возможность исключать нельзя.
Прилив
Два основных действующие на Марс приливные силы — это солнечный прилив и прилив Фобоса. Число Лява k2- важная пропорциональная безразмерная константа, связывающая приливное поле, действующее на тело, с мультиполярным моментом в результате массового распределения тела. Обычно k 2 может указывать на квадрупольную деформацию. Нахождение k 2 помогает понять внутреннюю структуру Марса. Наиболее актуальное значение k 2, полученное командой Генуи, составляет 0,1697 ± 0,0009. Если k 2 меньше 0,10, указано твердое ядро, это говорит о том, что, по крайней мере, внешнее ядро на Марсе жидкое, и прогнозируемый ядро ядра составляет 1520–1840 км.
Однако текущие данные радиотрекинга от MGS, ODY и MRO не позволяют эффект запаздывания фазы на приливы, поскольку он слишком слаб и требует более точных измерений возмущений космических аппаратов в будущем.
Геофизические последствия
Толщина земной коры
В настоящее время нет прямых измерений толщины земной коры на Марсе. Геохимические последствия от метеоритов SNC и ортопироксенита метеорита ALH84001 предполагают, что средняя толщина земной коры Марса составляет 100–250 км. Анализ вязкой релаксации показал, что максимальная толщина составляет 50–100 км. Такая толщина имеет решающее значение для поддержания изменений земной коры полушария и предотвращения руслового потока. Комбинированные исследования геофизики и геохимии показали, что средняя толщина земной коры может быть до 50 ± 12 км.
Измерение гравитационного поля различными орбитальными аппаратами позволяет создать глобальную модель с более высоким разрешением. При локальных аномалиях мелкой плотности и устранении эффекта создается остаточный потенциал конструкции, как показано в следующем уравнении:
URB = UB — U core — U local { displaystyle U_ {RB} = U_ {B} -U_ {core} — U_ {local}}

Остаточный потенциал Буг вносит за счет мантии. Волнистость границы кора-мантия или поверхности Мохо с поправкой массы на местности должна быть к остаточным аномалиям. В свою очередь, если наблюдается волнистая граница, должны быть изменения толщины земной коры.
Глобальное исследование данных об остаточной аномалии Буге показывает, что толщина коры Марса изменяется от 5,8 км до 102 км. Два основных пика на 32 км и 58 км идентифицируются по гистограмме толщины земной коры с равной площадью. Эти два пика связаны с дихотомией земной коры Марса. Почти вся кора толщиной более 60 км представлена южным нагорьем, в целом однородной по мощности. А северная низменность вообще имеет более тонкую корку. Установлено, что мощность земной коры региона Arabia Terra и северного полушария зависит от широты. Чем дальше на юг в сторону Sinai Planum и Lunae Planum, тем более утолщена кора.

Среди всех регионов Таумазия и Кларитис содержат самую толстую часть коры на Марсе, которая составляет гистограмму>70 км. В бассейнех Эллада и Аргир кора тоньше 30 км, что является исключительно тонкой областью в южном полушарии. Исид и Утопия также значительное истончение коры, причем в центре бассейнов Исидиса, как полагают, самая тонкая кора на Марсе.
Перераспределение коры за счет ударов и вязкой релаксации

Предполагается, что утонение произошло под почти всеми ударными кратерами. Возможными причинами являются выемка земной коры, модификация за счет внедрения вулканического материала и течения земной коры в слабой литосфере. После выкопки коры до удара гравитационное восстановление будет происходить за счет поднятия центральной мантии, так что дефицит массы полости может быть компенсирован массой поднятого более плотного материала.
Гигантские ударные бассейны Утопия, Эллада, Аргире и Исидис — одни из самых ярких примеров. Утопия, ударный бассейн, расположенный в северной низменности, заполнен легкими и водными осадочными отложениями и имеет слегка утолщенную корку в центре. Это возможно из-за большого процесса шлифовки в северной низменности. В то время как для бассейнов Эллада, Аргир и Исидис они имеют большой приподнятый рельеф Мохо и обнаруживают кольца диффузной утолщенной коры за краем земной коры.
Но напротив, почти все марсианские бассейны диаметром 275 км аномалию силы тяжести в свободном воздухе, хотя данные показывают, что все они должны были испытывать сильную гравитацию (положительная аномалия силы тяжести в свободном воздухе). Было высказано предположение, что это вызвано не только эрозией и захоронением, поскольку добавление материала в бассейн на самом деле увеличило бы силу тяжести, а не уменьшило бы ее. Так должно было произойти. Высокий тепловой поток и высокое содержание воды в ранней марсианской коре способствовали вязкой релаксации. Эти два фактора сделали корку более пластичной. Топография бассейна кратеров будет подвергаться большему напряжению из-за самогравитации. Такое напряжение привело бы к течению земной коры и, следовательно, к распаду рельефа. Исключение составляют гигантские ударные бассейны, которые не испытали вязкой релаксации, поскольку истончение коры сделало ее слишком тонкой для поддержания субсолидусного потока коры.
Низкая объемная плотность коры
Самый последний Модель RM1, разработанная в 2017 году, дает для Марса 2582 ± 209 кг · м, что представляет собой среднемировое значение. Боковое изменение плотности земной коры должно существовать. Например, над вулканическими комплексами ожидается, что местная плотность достигнет 3231 ± 95 кг · м, что соответствует метеоритным данным и предыдущим оценкам. Вдобавок плотность северного полушария в целом выше, чем плотность южного полушария, что может означать, что последний пористый, чем первый.
Для достижения объемного значения пористость может сыграть роль роли. Если плотность минерального зерна выбрана равной 3100 кг / м, пористость от 10% до 23% может привести к падению насыпной плотности на 200 кг / м. Если поровые пространства заполнены водой или льдом, также ожидается уменьшение объемной плотности. Дальнейшее падение плотности плотности может быть увеличено, при этом поверхностный слой более пористый, чем более глубокий Марс, а объем плотности с глубиной также имеет географические вариации.
Технические и научные приложения
Ареоид

ареоид представляет гравитационную и вращательную эквипотенциальную фигуру Марса, аналогично концепции геоида («уровень моря ») на Земле. Это было установлено в качестве основы для разработки MOLA (MEGDRs), которая является глобальной топографической моделью. Модель топографии важна для картирования геоморфологических особенностей и понимания различных процессов на Марсе.
Для получения ареоида требуются две части работы. Во-первых, данные о гравитации важны для определения положения центра планеты, которое в степени влияет на распределение массы внутри, необходимы данные радиосопровождения космических аппаратов. Этим в основном занимался Mars Global Сюрвейер (MGS). Затем прибор MOLA 2 на борту MGS, который работает на орбите возвышения 400 км, мог бы измерить расстояние между космическим кораблем и поверхностью земли путем подсчета времени полета и полета обратно. пульс от прибора. Комбинация этих двух работ позволяет построить ареоид, а также MEGDR. Исходя из вышеизложенного, радиус ареоида был принят за средний радиус планеты на экваторе, равный 3396 км.
Посадка на поверхности
Так как между Марсом и Землей большое расстояние, Немедленное управление посадочным модулем практически невозможно, и посадка во многом зависит от его автономной системы. Это было признано, что во избежание неудач точное понимание гравитационного поля Марса для проектов посадки, так что компенсирующие факторы и неопределенности эффектов могут быть минимизированы, плавный посадки. Первый в истории искусственный объект, приземлившийся на Марс, посадочный модуль Mars 2 потерпел крушение по неизвестной причине. Использование трехмерной среды в трехмерной среде. Использование трехмерных изображений. Лидар на месте для определения точного положения приземления и других защитных средств. меры.
Ссылки
Солнечная система > Система Марс > Планета Марс > Гравитация на Марсе
Земля и Марс во многом похожи. Они практически сходятся по площади поверхности, обладают полярными шапками, осевым наклоном и сезонной изменчивостью. К тому же обе показывают, что прошли сквозь климатические перемены.
Но они и отличаются. И одним из важнейших факторов выступает гравитация. Поверьте, если вы собираетесь колонизировать чужой мир, то этот момент сыграет важную роль.
Эта анимация наглядно показывает, на какую высоту смог бы подпрыгнуть человек, находясь на Марсе
Сравнение гравитации на Марсе и Земле
Мы знаем, что земные условия помогли сформироваться жизни, поэтому используем их в качестве ориентира при поиске чужой. Атмосферное давление на Марсе – 7.5 миллибар против 1000 земного. Средний показатель температуры поверхности опускается к -63°C, а у нас – 14°C. На фото отобразили строение Марса.
Художественная интерпретация марсианского интерьера
Если длина марсианского дня почти сходится с земным (24 часа и 37 минут), то год охватывает целых 687 дней. Марсианская гравитация на 62% ниже земного показателя, то есть 100 кг там переходят в 38 кг.
На подобное отличие влияют масса, радиус и плотность. Несмотря на схожесть в площади поверхности, Марс охватывает лишь половину земного диаметра, 15% от объема и 11% массивности. А что с силой тяжести Марса?
Вычисление гравитации Марса
Для определения марсианской гравитации исследователи использовали теорию Ньютона: гравитация выступает пропорциональной массе. Мы сталкиваемся со сферическим телом, поэтому гравитация будет обратно пропорциональная квадрату радиуса. Ниже представлена карта гравитации Марса.
Гравитационная карта Марса
Пропорции выражаются формулой g = m/r2, где g – поверхностная гравитация (кратная земной = 9.8 м/с²), m – масса (кратная земной = 5.976 · 1024 кг), а r – радиус (кратный земному = 6371 км).
Марсианская масса – 6.4171 х 1023 кг, что в 0.107 раза больше нашей. Средний радиус – 3389.5 км = 0.532 земного. Математически: 0.107/0.532² = 0.376.
Хотите получить индивидуальный расклад?
Опытный таролог ответит на вопросы:
Что ждёт Вас в будущем? Как сложатся отношения? Какое решение — верное?
Мы не знаем, что случится с человеком, если его окунуть в подобные условия на длительный срок. Но изучение воздействия микрогравитации показывает потерю мышечной массы, плотности костей, удары по органам и снижение зрения.
Прежде чем отправляться на планету, мы должны детально изучить ее гравитацию, иначе колония обречена на гибель.
Художественное видение марсианского астронавта
Уже есть проекты, которые занимаются этим моментом. Так Марс-1 разрабатывает программы по улучшению мускулатуры. Пребывание на МКС дольше 4-6 месяц показывает потерю мышечной массы на 15%.
Но марсианская займет намного больше времени на сам полет, где корабль атакуется космическими лучами, и пребывание на планете, где также нет защитного магнитного слоя. Экипажные миссии 2030-х гг. все ближе, поэтому мы должны поставить решение этих вопросов в приоритет. Теперь вы знаете, как выглядит гравитация на Марсе.
Читайте также:
- Интересные факты о Марсе;
- Колонизация Марса;
- Марс и Земля;
- Есть ли жизнь на Марсе;
- Терраформирование Марса
- Когда мы отправим людей на Марс?
- Сравнение Марса и Земли
- Как Земля выглядит с Марса?
- Что такое марсианское проклятие?
- Когда открыли Марс?
Положение и движение Марса
- Орбита Марса;
- Сезоны на Марсе
- Как далеко Марс от Солнца?
- Сближение Марса
- Как далеко находится Марс?
- Сколько лететь до Марса;
- День на Марсе;
- Год на Марсе;
Строение Марса
- Размеры Марса;
- Кольца Марса;
- Состав Марса;
- Атмосфера Марса;
- Воздух на Марсе;
- Масса Марса;
Поверхность Марса
- Поверхность Марса;
- Лед на Марсе
- Радиация на Марсе
- Вода на Марсе;
- Температура на Марсе;
- Гравитация на Марсе;
- Цвет Марса;
- Почему Марс красный;
- Насколько холодный Марс;
- Вулканы на Марсе;
- Вулкан Олимп;
- Долина Маринер;
- Лицо на Марсе;
- Пирамида на Марсе;