Magnets exert forces and torques on each other due to the rules of electromagnetism. The forces of attraction field of magnets are due to microscopic currents of electrically charged electrons orbiting nuclei and the intrinsic magnetism of fundamental particles (such as electrons) that make up the material. Both of these are modeled quite well as tiny loops of current called magnetic dipoles that produce their own magnetic field and are affected by external magnetic fields. The most elementary force between magnets is the magnetic dipole–dipole interaction. If all of the magnetic dipoles that make up two magnets are known then the net force on both magnets can be determined by summing up all these interactions between the dipoles of the first magnet and that of the second.
It is often more convenient to model the force between two magnets as being due to forces between magnetic poles having magnetic charges spread over them. Positive and negative magnetic charge is always connected by a string of magnetized material; isolated magnetic charge does not exist. This model works well in predicting the forces between simple magnets where good models of how the magnetic charge is distributed are available.
Magnetic poles vs. atomic currents[edit]
Magnetic-charge model for H and Ampère’s model for B yield the identical field outside of a magnet. Inside they are very different.
The field of a magnet is the sum of fields from all magnetized volume elements, which consist of small magnetic dipoles on an atomic level. The direct summation of all those dipole fields would require three-dimensional integration just to obtain the field of one magnet, which may be intricate.
In case of a homogeneous magnetization, the problem can be simplified at least in two different ways, using Stokes’ theorem. Upon integration along the direction of magnetization, all dipoles along the line of integration cancel each other, except at the magnet’s end surface. The field then emerges only from those (mathematical) magnetic charges spread over the magnet’s end facets. On the contrary, when integrating over a magnetized area orthogonal to the direction of magnetization, the dipoles within this area cancel each other, except at the magnet’s outer surface, where they (mathematically) sum up to a ring current. This is called Ampère model. In both models, only two-dimensional distributions over the magnet’s surface have to be considered, which is simpler than the original three-dimensional problem.
Magnetic-charge model: In the magnetic-charge model, the pole surfaces of a permanent magnet are imagined to be covered with so-called magnetic charge, north pole particles on the north pole and south pole particles’ on the south pole, that are the source of the magnetic field lines. The field due to magnetic charges is obtained through Coulomb’s law with magnetic instead of electric charges. If the magnetic pole distribution is known, then the pole model gives the exact distribution of the magnetic field intensity H both inside and outside the magnet. The surface charge distribution is uniform, if the magnet is homogeneously magnetized and has flat end facets (such as a cylinder or prism).
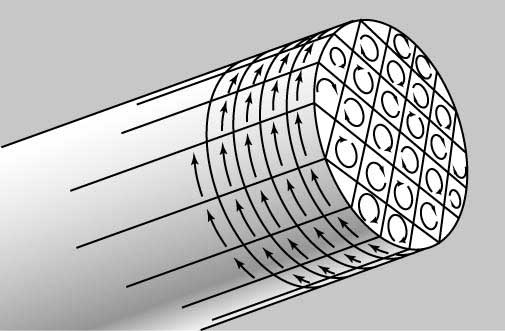
Ampère model: In the Ampère model, all magnetization is due to the effect of microscopic, or atomic, circular bound currents, also called Ampèrian currents throughout the material. The net effect of these microscopic bound currents is to make the magnet behave as if there is a macroscopic electric current flowing in loops in the magnet with the magnetic field normal to the loops. The field due to such currents is then obtained through the Biot–Savart law. The Ampère model gives the correct magnetic flux density B both inside and outside the magnet. It is sometimes difficult to calculate the Ampèrian currents on the surface of a magnet.
Magnetic dipole moment[edit]
Far away from a magnet, its magnetic field is almost always described (to a good approximation) by a dipole field characterized by its total magnetic dipole moment, m. This is true regardless of the shape of the magnet, so long as the magnetic moment is non-zero. One characteristic of a dipole field is that the strength of the field falls off inversely with the cube of the distance from the magnet’s center.
The magnetic moment of a magnet is therefore a measure of its strength and orientation. A loop of electric current, a bar magnet, an electron, a molecule, and a planet all have magnetic moments. More precisely, the term magnetic moment normally refers to a system’s magnetic dipole moment, which produces the first term in the multipole expansion[note 1] of a general magnetic field.
Both the torque and force exerted on a magnet by an external magnetic field are proportional to that magnet’s magnetic moment. The magnetic moment is a vector: it has both a magnitude and direction. The direction of the magnetic moment points from the south to north pole of a magnet (inside the magnet). For example, the direction of the magnetic moment of a bar magnet, such as the one in a compass is the direction that the north poles points toward.
In the physically correct Ampère model, magnetic dipole moments are due to infinitesimally small loops of current. For a sufficiently small loop of current, I, and area, A, the magnetic dipole moment is:
where the direction of m is normal to the area in a direction determined using the current and the right-hand rule. As such, the SI unit of magnetic dipole moment is ampere meter2. More precisely, to account for solenoids with many turns the unit of magnetic dipole moment is ampere–turn meter2.
In the magnetic-charge model, the magnetic dipole moment is due to two equal and opposite magnetic charges that are separated by a distance, d. In this model, m is similar to the electric dipole moment p due to electrical charges:
where qm is the ‘magnetic charge’. The direction of the magnetic dipole moment points from the negative south pole to the positive north pole of this tiny magnet.
Magnetic force due to non-uniform magnetic field[edit]
Top: 
, the force on magnetic north-poles.
Bottom: 
, the force on aligned dipoles, such as iron particles.
Magnets are drawn along the magnetic field gradient. The simplest example of this is the attraction of opposite poles of two magnets. Every magnet produces a magnetic field that is stronger near its poles. If opposite poles of two separate magnets are facing each other, each of the magnets is drawn into the stronger magnetic field near the pole of the other. If like poles are facing each other, though, they are repulsed from the larger magnetic field.
The magnetic-charge model predicts a correct mathematical form for this force and is easier to understand qualitatively. For if a magnet is placed in a uniform magnetic field then both poles will feel the same magnetic force but in opposite directions, since they have opposite magnetic charge. But, when a magnet is placed in the non-uniform field, such as that due to another magnet, the pole experiencing the large magnetic field will experience the large force and there will be a net force on the magnet. If the magnet is aligned with the magnetic field, corresponding to two magnets oriented in the same direction near the poles, then it will be drawn into the larger magnetic field. If it is oppositely aligned, such as the case of two magnets with like poles facing each other, then the magnet will be repelled from the region of higher magnetic field.
In the Ampère model, there is also a force on a magnetic dipole due to a non-uniform magnetic field, but this is due to Lorentz forces on the current loop that makes up the magnetic dipole. The force obtained in the case of a current loop model is
where the gradient ∇ is the change of the quantity m · B per unit distance, and the direction is that of maximum increase of m · B. To understand this equation, note that the dot product m · B = mB cos(θ), where m and B represent the magnitude of the m and B vectors and θ is the angle between them. If m is in the same direction as B then the dot product is positive and the gradient points ‘uphill’ pulling the magnet into regions of higher B-field (more strictly larger m · B). B represents the strength and direction of the magnetic field. This equation is strictly only valid for magnets of zero size, but is often a good approximation for not too large magnets. The magnetic force on larger magnets is determined by dividing them into smaller regions having their own m then summing up the forces on each of these regions.
Magnetic-charge model[edit]
The magnetic-charge model assumes that the magnetic forces between magnets are due to magnetic charges near the poles. This model works even close to the magnet when the magnetic field becomes more complicated, and more dependent on the detailed shape and magnetization of the magnet than just the magnetic dipole contribution. Formally, the field can be expressed as a multipole expansion: A dipole field, plus a quadrupole field, plus an octopole field, etc. in the Ampère model, but this can be very cumbersome mathematically.
Calculating the magnetic force[edit]
Calculating the attractive or repulsive force between two magnets is, in the general case, a very complex operation, as it depends on the shape, magnetization, orientation and separation of the magnets. The magnetic-charge model does depend on some knowledge of how the ‘magnetic charge’ is distributed over the magnetic poles. It is only truly useful for simple configurations even then. Fortunately, this restriction covers many useful cases.
Force between two magnetic poles[edit]
If both poles are small enough to be represented as single points then they can be considered to be point magnetic charges. Classically, the force between two magnetic poles is given by:[1]
where
- F is force (SI unit: newton)
- qm1 and qm2 are the magnitudes of magnetic charge on magnetic poles (SI unit: ampere-meter)
- μ is the permeability of the intervening medium (SI unit: tesla meter per ampere, henry per meter or newton per ampere squared)
- r is the separation (SI unit: meter).
The pole description is useful to practicing magneticians who design real-world magnets, but real magnets have a pole distribution more complex than a single north and south. Therefore, implementation of the pole idea is not simple. In some cases, one of the more complex formulas given below will be more useful.
Force between two nearby magnetized surfaces of area A[edit]
The mechanical force between two nearby magnetized surfaces can be calculated with the following equation. The equation is valid only for cases in which the effect of fringing is negligible and the volume of the air gap is much smaller than that of the magnetized material, the force for each magnetized surface is:[2][3][4]
where:
- A is the area of each surface, in m2
- H is their magnetizing field, in A/m.
- μ0 is the permeability of space, which equals 4π×10−7 T·m/A
- B is the flux density, in T
The derivation of this equation is analogous to the force between two nearby electrically charged surfaces,[5] which assumes that the field in between the plates is uniform.
Force between two bar magnets[edit]
Field of two attracting cylindrical bar magnets
Field of two repelling cylindrical bar magnets
The force between two identical cylindrical bar magnets placed end to end at great distance 
is approximately:[2]
![{displaystyle Fsimeq left[{frac {B_{0}^{2}A^{2}left(L^{2}+R^{2}right)}{pi mu _{0}L^{2}}}right]left[{frac {1}{x^{2}}}+{frac {1}{(x+2L)^{2}}}-{frac {2}{(x+L)^{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc92f379ff8aae485e69ac2ec29922683f34f5bc)
where
- B0 is the flux density very close to each pole, in T,
- A is the area of each pole, in m2,
- L is the length of each magnet, in m,
- R is the radius of each magnet, in m, and
- x is the separation between the two magnets, in m
relates the flux density at the pole to the magnetization of the magnet.
Note that these formulations assume point-like magnetic-charge distributions instead of a uniform distribution over the end facets, which is a good approximation only at relatively great distances. For intermediate distances, numerical methods must be used.
Force between two cylindrical magnets[edit]
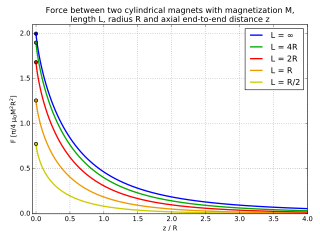
Exact force between two coaxial cylindrical bar magnets for several aspect ratios.
For two cylindrical magnets with radius 
, and length 
, with their magnetic dipole aligned, the force can be computed analytically using elliptic integrals.[6] In the limit , the force can be approximated by,[7]
![{displaystyle F(x)simeq {frac {pi mu _{0}}{4}}M^{2}R^{4}left[{frac {1}{x^{2}}}+{frac {1}{(x+2L)^{2}}}-{frac {2}{(x+L)^{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d5e14e711ed8016824a1b162737b7c17e2b4ecd)
Where 
is the magnetization of the magnets and 
is the distance between them. For small values of , the results are erroneous as the force becomes large for close-to-zero distance.
If the magnet is long (
), a measurement of the magnetic flux density very close to the magnet 
is roughly related to by the formula
The effective magnetic dipole moment can be written as
where 
is the volume of the magnet. For a cylinder this is 
, and is the magnetisation field of the dipole.
When 
the point dipole approximation is obtained,
Which matches the expression of the force between two magnetic dipoles.
Ampère model[edit]
French scientist André Marie Ampère found that the magnetism produced by permanent magnets and the magnetism produced by electromagnets are the same kind of magnetism. Because of that, the strength of a permanent magnet can be expressed in the same terms as that of an electromagnet.
The strength of magnetism of an electromagnet that is a flat loop of wire through which a current flows, measured at a distance that is great compared to the size of the loop, is proportional to that current and is proportional to the surface area of that loop.
For purpose of expressing the strength of a permanent magnet in same terms as that of an electromagnet, a permanent magnet is thought of as if it contains small current-loops throughout its volume, and then the magnetic strength of that magnet is found to be proportional to the current of each loop (in amperes), and proportional to the surface of each loop (in square meters), and proportional to the density of current-loops in the material (in units per cubic meter), so the dimension of strength of magnetism of a permanent magnet is amperes times square meters per cubic meter, is amperes per meter.
That is why ampere per meter is the correct unit of magnetism, even though these small current loops are not really present in a permanent magnet.
The validity of Ampère’s model means that it is allowable to think of the magnetic material as if it consists of current-loops, and the total effect is the sum of the effect of each current-loop, and so the magnetic effect of a real magnet can be computed as the sum of magnetic effects of tiny pieces of magnetic material that are at a distance that is great compared to the size of each piece.
This is very useful for computing magnetic force-field of a real magnet; It involves summing a large amount of small forces and you should not do that by hand, but let your computer do that for you; All that the computer program needs to know is the force between small magnets that are at great distance from each other.
In such computations it is often assumed that each (same-size) small piece of magnetic material has an equally strong magnetism, but this is not always true: a magnet that is placed near another magnet can change the magnetization of that other magnet. For permanent magnets this is usually only a small change, but if you have an electromagnet that consists of a wire wound round an iron core, and you bring a permanent magnet near to that core, then the magnetization of that core can change drastically (for example, if there is no current in the wire, the electromagnet would not be magnetic, but when the permanent magnet is brought near, the core of the electromagnet becomes magnetic).
Thus the Ampère model is suitable for computing the magnetic force-field of a permanent magnet, but for electromagnets it can be better to use a magnetic-circuit approach.
Magnetic dipole–dipole interaction[edit]
If two or more magnets are small enough or sufficiently distant that their shape and size is not important then both magnets can be modeled as being magnetic dipoles having a magnetic moments m1 and m2. In case of uniformly magnetized spherical magnets this model is precise even at finite size and distance, as the outside field of such magnets is exactly a dipole field.[8]
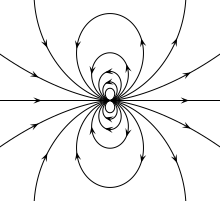
Magnetic field of an ideal dipole.
The magnetic field of a magnetic dipole in vector notation is:
where
- B is the field
- r is the vector from the position of the dipole to the position where the field is being measured
- r is the absolute value of r: the distance from the dipole
is the unit vector parallel to r;- m is the (vector) dipole moment
- μ0 is the permeability of free space
- δ3 is the three-dimensional delta function.[note 2]
This is exactly the field of a point dipole, exactly the dipole term in the multipole expansion of an arbitrary field, and approximately the field of any dipole-like configuration at large distances.
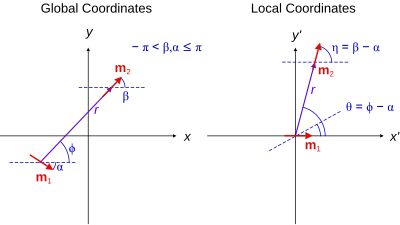
Frames of reference for calculating the forces between two dipoles
Force between coaxial cylinder magnets. According to the dipole approximation, the force drops proportional to 
for large distance z, resulting in slopes of −4 in the log–log plot.
If the coordinate system is shifted to center it on m1 and rotated such that the x-axis points in the direction of m1 then the previous equation simplifies to[9]
where the variables r and θ are measured in a frame of reference with origin in m1 and oriented such that m1 is at the origin pointing in the x-direction. This frame is called Local coordinates and is shown in the Figure on the right.
The force of one magnetic dipole on another is determined by using the magnetic field of the first dipole given above and determining the force due to the magnetic field on the second dipole using the force equation given above. Using vector notation, the force of a magnetic dipole m1 on the magnetic dipole m2 is:
![{displaystyle mathbf {F} (mathbf {r} ,mathbf {m} _{1},mathbf {m} _{2})={frac {3mu _{0}}{4pi r^{5}}}left[(mathbf {m} _{1}cdot mathbf {r} )mathbf {m} _{2}+(mathbf {m} _{2}cdot mathbf {r} )mathbf {m} _{1}+(mathbf {m} _{1}cdot mathbf {m} _{2})mathbf {r} -{frac {5(mathbf {m} _{1}cdot mathbf {r} )(mathbf {m} _{2}cdot mathbf {r} )}{r^{2}}}mathbf {r} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78b7d23c669207fabcaa1f93182cccc27f189839)
where r is the distance-vector from dipole moment m1 to dipole moment m2, with r = ‖r‖. The force acting on m1 is in opposite direction. As an example the magnetic force for two magnets pointing in the z-direction and aligned on the z-axis and separated by the distance z is:
- , z-direction.
The final formulas are shown next. They are expressed in the global coordinate system,
![{displaystyle {begin{aligned}F_{r}(mathbf {r} ,alpha ,beta )&=-{frac {3mu _{0}}{4pi }}{frac {m_{2}m_{1}}{r^{4}}}left[2cos(phi -alpha )cos(phi -beta )-sin(phi -alpha )sin(phi -beta )right]\F_{phi }(mathbf {r} ,alpha ,beta )&=-{frac {3mu _{0}}{4pi }}{frac {m_{2}m_{1}}{r^{4}}}sin(2phi -alpha -beta )end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44fa313e3fcd5fa92d555d5a7f90fc91616916c4)
Notes[edit]
- ^ The magnetic dipole portion of the magnetic field can be understood as being due to one pair of north/south poles. Higher order terms such as the quadrupole can be considered as due to 2 or more north/south poles ordered such that they have no lower order contribution. For example the quadrupole configuration has no net dipole moment.
- ^ δ3(r) = 0 except at r = (0, 0, 0), so this term is ignored in multipole expansion.
References[edit]
- ^ «Basic Relationships». Geophysics.ou.edu. Archived from the original on 2010-07-09. Retrieved 2009-10-19.
- ^ a b «Magnetic Fields and Forces». Archived from the original on February 20, 2012. Retrieved 2009-12-24.
- ^ «The force produced by a magnetic field». Retrieved 2013-11-07.
- ^ «Tutorial: Theory and applications of the Maxwell stress tenso» (PDF). Retrieved 2018-11-28.
- ^ «Force Acting on Capacitor Plates — Collection of Solved Problems». physicstasks.eu. Retrieved 2020-01-20.
- ^ Ravaud, R; Lemarquand, G; Babic, S; Lemarquand, V; Akyel, C (2010). «Cylindrical magnets and coils: Fields, forces, and inductances». IEEE Transactions on Magnetics. 46 (9): 3585–3590. Bibcode:2010ITM….46.3585R. doi:10.1109/TMAG.2010.2049026. S2CID 25586523.
- ^ Vokoun, David; Beleggia, Marco; Heller, Ludek; Sittner, Petr (2009). «Magnetostatic interactions and forces between cylindrical permanent magnets». Journal of Magnetism and Magnetic Materials. 321 (22): 3758–3763. Bibcode:2009JMMM..321.3758V. doi:10.1016/j.jmmm.2009.07.030.
- ^ Lehner, Günther (2008). Electromagnetic Field Theory for Engineers and Physicists. p. 309. doi:10.1007/978-3-540-76306-2. ISBN 978-3-540-76305-5. S2CID 117970017.
- ^
Schill, R. A. (2003). «General relation for the vector magnetic field of a circular current loop: A closer look». IEEE Transactions on Magnetics. 39 (2): 961–967. Bibcode:2003ITM….39..961S. doi:10.1109/TMAG.2003.808597.
See also[edit]
- Magnetic motor
Главная >> Применение >> Типовые примеры >>
Притяжение цилиндрических постоянных магнитов
магнит, магнитное поле, сила, притяжение, моделирование магнитного поля магнита, расчет силы магнита, моделирование притяжения магнита
Два одинаковых постоянных магнита притягиваются друг к другу.
Тип задачи
Осесимметричная задача магнитостатики
Геометрия
Притяжение цилиндрических постоянных магнитов
Два одинаковых постоянных магнита притягиваются друг к другу
Постоянный магнит
δ
l
D
D = 2″ (50.8 мм) диаметр магнитов;
l = 0.65″ (16.51 мм) — толщина магнитов;
δ=0.5″ (12.7 мм) — расстояние между магнитами;
Дано
Два магнита марки N35, Hc = 954930 А/м, Br = 1.26 Тл;
Задание
Рассчитать силу притяжения двух постоянных магнитов.
Решение
Для расчета пондеромоторной силы необходимо окружить контуром интегрирования один из магнитов.
Результат
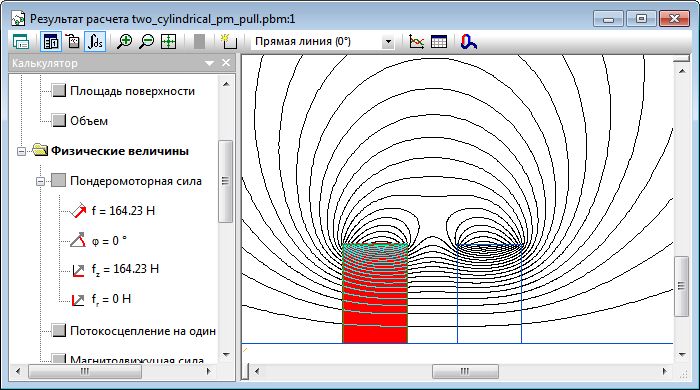
Сила притяжения двух постоянных магнитов: f = 164 Н
Значение, приводимое фирмой-изготовителем www.kjmagnetics.com: f = 153 Н (33.77 фунта, 1 фунт = 4.54 Н)
- Видео: Притяжение цилиндрических постоянных магнитов
- Смотреть на YouTube.
- Скачать файлы задачи
Немного истории
Происхождение слова «магнит» покрыто тайной. Ученые склоняются к версии названия, произошедшего от имени греческого пастуха Магнеса, пастух нашел минерал и был удивлен его свойствам. Другая неподтвержденная гипотеза: минерал назван так в честь региона Магнесия, находившегося в Малой Азии. В этом районе были открыты залежи магнетита.
Почему магниты имеют свойство притягиваться и отталкиваться
Магнетизм, как научное явление, вызывается перемещением электронов. Вещества и предметы состоят из мельчайших атомов, эта физическая единица представляет собой ядро и движущиеся вокруг него электроны. Поскольку электроны имеют отрицательные заряды, то создают магнитные поля. Вращение электрона по часовой стрелке направляет магнитное поле наверх, а вращение против часовой стрелки – вниз.
Если количество разнонаправленных полей совпадает, то магнитные поля отсутствуют. Если баланс нарушается, и электроны начинают вращение в одном направлении, возникает магнитное поле большой силы. Именно этот процесс и происходит в минерале под названием магнетит.
У магнита два полюса: северный и южный. Если два магнита расположить вблизи, они начинают направлять магнитные поля строго в одном направлении, другими словами, усиливать друг друга. Южный полюс первого магнита стремится к северному полюсу второго. Если вблизи оказываются пара северных или пара южных полюсов магнитов, их магнитные поля направляются в разные стороны, и магниты отталкиваются.
В структуре железа происходят приблизительно такие же процессы, электроны производят вращение в одну сторону. Если рядом появляется магнит, железо воспринимает его как близкий по структуре материал и стремится соединить свои магнитные поля с полями минерала. Железо само становится магнитом, находясь рядом с минералом. Пока железо и магнит притянуты друг к другу, их магнитные поля остаются в параллельном направлении. Как только они разъединяются, магнитные свойства железа исчезают.
Определение притяжения и отталкивания магнетизма
Если иметь в виду направление векторовv1, v2, а такжер, вы можете определить, является ли сила между ними притягивающей или отталкивающей. Например, если у вас есть частица, движущаяся вперед в направлении x со скоростьюv, то это значение должно быть положительным. Если он движется в другом направлении, то значение v должно быть отрицательным.
Эти две частицы отталкиваются друг от друга, если магнитные силы, определяемые их соответствующими магнитными полями между ними, нейтрализуют друг друга, указывая в разных направлениях друг от друга. Если две силы направлены в разные стороны друг к другу, магнитная сила притягивает. Магнитная сила вызвана этими движениями частиц.
Вы можете использовать эти идеи, чтобы показать, как магнетизм работает с повседневными предметами. Например, если вы поместите неодимовый магнит рядом со стальной отверткой и переместите его вверх, вниз по валу, а затем удалите магнит, отвертка может сохранить в нем некоторый магнетизм. Это происходит из-за взаимодействующих магнитных полей между двумя объектами, которые создают силу притяжения, когда они нейтрализуют друг друга.
Это определение «отталкивать и притягивать» справедливо во всех случаях использования магнитов и магнитных полей. Следите за тем, какие направления соответствуют отталкиванию и притяжению.
Отталкивающая сила магнита
Противоположности притягиваются. Чтобы объяснить, почему магниты отталкиваются друг от друга, северный конец одного магнита будет притягиваться к югу от другого магнита. Северный и северный концы двух магнитов, а также южный и южный концы двух магнитов будут отталкивать друг друга. Магнитная сила является основой электродвигателей и привлекательных магнитов для использования в медицине, промышленности и исследованиях.
Чтобы понять, как работает эта сила отталкивания, и объяснить, почему магниты отталкивают друг друга и притягивают электричество, важно изучить природу магнитной силы и множество форм, которые она принимает в различных явлениях в физика.
Расчет магнитных свойств
Магнитная индукция поля Земли составляет 0,5Ч10–4 Тл, тогда как поле между полюсами сильного электромагнита – порядка 2 Тл и более.
Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био – Савара – Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю.
Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называетсямагнитной восприимчивостью и обозначается греческой буквой c; c– безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma – абсолютная, а m – относительная проницаемости,
В ферромагнитных веществах величина c может иметь очень большие значения –до 104ё106. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных – немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3).
Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
Магнитная сила между проводами
Для токов, которые перемещают заряды по проводам, магнитная сила может быть определена как притягивающая или отталкивающий, основанный на расположении проводов относительно друг друга и направлении тока движется. Для токов в круглых проводах вы можете использовать правую руку, чтобы определить, как возникают магнитные поля.
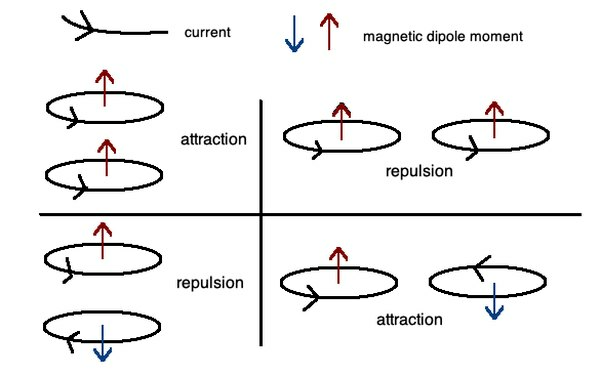
Правило правой руки для токов в петлях из проводов означает, что если вы поместите пальцы правой руки, согнутые в направлении проволочной петли, вы можете определить направление результирующего магнитного поля и магнитный момент, как показано на схеме выше. Это позволяет определить, насколько петли привлекательны или отталкивают друг друга.
Правило правой руки также позволяет определить направление магнитного поля, которое излучает ток в прямом проводе. В этом случае вы указываете большим пальцем правой руки в направлении тока через электрический провод. Направление сгибания пальцев правой руки определяет направление магнитного поля?
Из этих примеров магнитного поля, индуцированного токами, вы можете определить магнитную силу между двумя проводами в результате формирования этих силовых линий магнитного поля.
Определение притяжения и отталкивания электричества
Магнитные поля между витками токоведущих проводов являются либо притягивающими, либо отталкивающими, в зависимости от направления электрического тока и направления возникающих из них магнитных полей. Магнитный дипольный момент – это сила и ориентация магнита, создающего магнитное поле. На приведенной выше диаграмме результирующее притяжение или отталкивание показывает эту зависимость.
Вы можете представить себе силовые линии магнитного поля, излучаемые этими электрическими токами, как вьющиеся вокруг каждой части токовой петли. Если направления петли между двумя проводами противоположны друг другу, провода будут притягиваться друг к другу. Если они находятся в противоположных направлениях друг от друга, петли будут отталкивать друг друга.
Магнитная проницаемость и ее роль в магнетизме
Магнитная проницаемость m – это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями – от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля.
На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1–3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов – таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.
Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой – сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Почему сила магнита действует по-разному?
В других материалах электроны движутся в разных направлениях, поэтому не могут создать сильное магнитное поле, не способны притягивать магниты.
Магнит притягивается с разной силой к различным металлам. К примеру, к никелю, железу и другим сплавам магнит притягивается очень прочно. Подавляющая часть металлов не взаимодействует с магнитами с такой силой, взаимодействие иногда невозможно заметить в домашних условиях, а только в лабораториях, во время проведения опытов. Строение и связь атомов у других металлов отличны от строения и связей железа, поэтому притяжение столь малозаметно.
По какой причине не все материалы способны магнититься
Магнит взаимодействует с широким перечнем веществ. Вид взаимодействия не ограничивается притяжением или отталкиванием. Отдельные металлы и сплавы обладают специфическим строением, что дает возможность притягиваться к магниту с определенной мощностью.
Другие материалы также обладают данным свойством, но в меньших масштабах. Чтобы зафиксировать притяжение в таких условиях, необходимо создание очень сильного магнитного поля. Это невыполнимо в домашних условиях. Почему свойство притяжения есть у всех материалов, а магнититься доступно для восприятия только металл? Разгадка заключается в особом внешнем строении атомов.
Окружающие нас вещи состоят из атомов, связанных между собой. Тип связи между ними определяет материал. Атомы в большинстве веществ плохо сгруппированы, поэтому связь с магнитом формируется слабая. В металле атомы хорошо скоординированы, все атомы синхронно ощущают магнитное поле и тянутся к нему.
Предыдущая
ИнверторыЧто такое преобразователь напряжения
Содержание книги
Предыдующая страница
§13. Взаимодействие магнитного поля с веществом
13.5 Взаимодействие постоянных магнитов.
Знание формы и намагниченности постоянного магнита позволяет для расчетов заменить его эквивалентной системой электрических токов намагничивания. Такая замена возможна как при расчете характеристик магнитного поля, так и при расчетах сил, действующих на магнит со стороны внешнего поля.
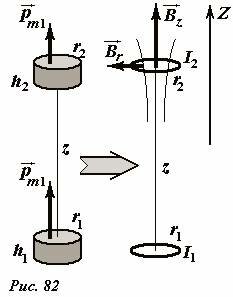
Для примера проведем расчет силы взаимодействия двух постоянных магнитов. Пусть магниты имеют форму тонкого цилиндра, их радиусы обозначим r1 и r2, толщины h1, h2 , оси магнитов совпадают, расстояние между магнитами обозначим z, будем считать, что оно значительно больше размеров магнитов (Рис. 82).
Возникновение силы взаимодействия между магнитами объясняется традиционным способом: один магнит создает магнитное поле, которое воздействует на второй магнит. Для расчета силы взаимодействия мысленно заменим магниты с однородной намагниченностью J1 и J2 круговыми токами, текущими по боковой поверхности цилиндров. Силы этих токов выразим через намагниченности магнитов
(~I_{1,2} = J_{1,2} h_{1,2}) , (1)
а их радиусы будем считать равными радиусам магнитов. Разложим вектор индукции (~vec B) магнитного поля, создаваемого первым магнитом в месте расположения второго на две составляющие: осевую (~vec B_z) , направленную вдоль оси магнита, и радиальную (~vec B_r) — перпендикулярную ей. Для вычисления суммарной силы, действующей на кольцо, необходимо мысленно разбить его на малые элементы IΔl и просуммировать силы Ампера, действующие на каждые такой элемент. Используя правило левой руки, легко показать, что осевая составляющая магнитного поля приводит к появлению сил Ампера, стремящихся растянуть (или сжать) кольцо – векторная сумма этих сил равна нулю. Наличие радиальной составляющей поля приводит к возникновению сил Ампера, направленных вдоль оси магнитов, то есть к их притяжению или отталкиванию.
Задание для самостоятельной работы.
- Убедитесь, что магниты притягиваются, если электрические токи текут в одном направлении, и отталкиваются, если токи текут в противоположных направлениях. Свяжите направления токов намагничивания с полюсами магнитов (северным и южным) и убедитесь, что разноименные полюса притягиваются, а одноименные отталкиваются.
Так как рассматриваемая система обладает осевой симметрией, то модуль радиальной составляющей постоянен во всех точках кольцевого тока второго магнита. Следовательно, проекция силы, действующей на второй магнит, с учетом правила левой руки, определяется формулой
(~F = -I_2 B_r l = -I_2 B_r 2 pi r_2) . (2)
Положительное направление силы соответствует притяжению магнитов, положительное направление тока традиционно – против часовой стрелки.
Магнитное поле, создаваемое первым магнитом, эквивалентно полю кругового тока (см. §12.7.1). В рамках сделанных приближений (z >> r,h), осевая составляющая поля определяется формулой
(~B_z = frac{mu_0 p_{m1}}{2 pi z^3}) , (3)
где (p_{m1} = I_1 S_1 = J_1 h_1 pi r^2_1 = J_1 V_1) — магнитный момент первого магнита (V1 — его объем).
Радиальную составляющую поля мы нашли с помощью о магнитном потоке, в месте расположения второго кругового контура она равна (см. §12.12)
(~B_r = -frac{r_2}{2} cdot frac{Delta B_z}{Delta z} = frac{3 mu_0 p_{m1}}{4 pi z^4} r_2) . (4)
Уменьшение осевой составляющей поля приводит к появлению положительной (направленной от оси) составляющей поля.
Важно подчеркнуть, что сила взаимодействия между магнитами определяется скоростью изменения[1] осевой составляющей поля (~frac{Delta B_z}{Delta z}), если бы поле, создаваемое первым магнитом было однородным, то сила, действующая на второй магнит, была бы равна нулю.
Этот вывод можно обобщить на случай произвольного контура с током (следовательно, и на любой постоянный магнит). Действительно, сила Ампера, действующая на элемент тока (~I Delta vec l_k) равна (~Delta vec F_k = I Delta vec l_k times vec B), для вычисления силы, действующей на контур необходимо просуммировать эти выражения по всем элементам контура
(~vec F = sum_k Delta vec F_k = sum_k I Delta vec l_k times vec B = I (sum_k Delta vec l_k) times vec B = vec 0)
При выводе учтено, что в однородном поле вектор индукции постоянен, поэтому его можно вынести за знак суммы, а сумма элементов контура равна нулю, так как все эти векторы выстроены в замкнутую линию – конец последнего совпадает с началом первого. Следовательно, сила действующая на любой постоянный магнит, находящийся во внешнем однородном поле равна нулю. Аналогично, сила, действующая на электрический диполь со стороны однородного электрического поля также равна нулю, а в неоднородном поле эта сила пропорциональна скорости изменения поля (~frac{Delta E}{Delta z}).
Подставляя выражение для радиальной составляющей поля, получим формулу, для вычисления силы взаимодействия двух магнитов в рассматриваемом случае
(~F = -I_2 cdot 2 pi r_2 cdot B_r = -I_2 cdot 2 pi r_2 cdot frac{3 mu_0 p_{m1}}{4 pi z^4} r_2 = I_2 cdot pi r^2_2 cdot frac{3 mu_0 p_{m1}}{2 pi z^4} = frac{3 mu_0 p_{m1} p_{m2}}{2 pi z^4}) . (5)
где (p_{m2} = I_2 S_2 = J_2 h_2 pi r^2_2 = J_2 V_2) — магнитный момент второго магнита. Так, например для двух одинаковых магнитов с размерами h = r = 1 см с намагниченностью J ≈ 4·105 А , находящихся на расстоянии z = 5 см сила взаимодействия приблизительно равна 0,15 Н.
Обратим внимание, что в формулу (5) в качестве характеристик магнитов входят только их магнитные моменты, поэтому эта формула может применяться для магнитов любой формы, важно только чтобы расстояние между ними превышало их размеры, и их магнитные моменты были параллельны. Также следует заметить, что сила взаимодействия между магнитами обратно пропорциональна четвертой степени расстояния между ними, что является следствием диполь-дипольного характера взаимодействия (для несуществующих точечных магнитных зарядов эта сила была бы, как обычно, обратно пропорциональна квадрату расстояния).
Примечания
- ↑ имеется ввиду скорость изменения величины поля в пространстве, а не с течением времени.
Следующая страница
Набери «Слободянюк А. И. Физика 10.13.5» там расчет для взаимодействия двух цилиндрических магнитов и пример.
Характерные поля постоянных магнитов — до 1 Тл (10 кг•с) .
Например для двух одинаковых магнитов с размерами h = r = 1 см с намагниченностью J ≈ 4•10^5 А, находящихся на расстоянии z = 5 см сила взаимодействия приблизительно равна 0,15 Н.
[ссылка заблокирована по решению администрации проекта]
F = — 3*Pm1*Pm2/(2*Pi*z^4) ( магнитные моменты)