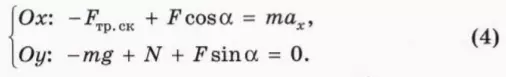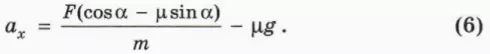Как найти силу приложенную под углом - AvtoShod.ru

Рассмотрим несколько задач на тему «вращательный момент» с пояснениями. Будем осуществлять расчет перпендикулярных частей сил и плеч сил в случаях, когда углы между силой и рычагом отличаются от прямого.

Это вторая часть статьи о моменте силы. Первая часть находится тут (откроется в новой вкладке).

Угол между силой и рычагом отличается от прямого

Рассмотрим рисунок 1. На рисунке 1а сила приложена к рукоятке ключа под прямым углом. На рисунках 1б и 1в углы между силой и рукояткой (рычагом) отличаются от прямого.

Рис. 1. Несколько способов приложения силы к рычагу под различными углами

Длина рычага является расстоянием между точкой приложения силы и осью вращения. Когда угол отличается от прямого, для вычисления момента силы нужно раскладывать на проекции либо силу, либо длину рычага (рукоятки).

Раскладываем силу

Разложим приложенную силу ( F ) на части. Одна часть будет располагаться перпендикулярно рукоятке, а другая – параллельно (см. рис. 2).

Рис. 2. Способ разложения силы, приложенной к рычагу под тупым (а) и острым (б) углами

Рукоятку вращает только перпендикулярная часть силы. На рисунке 2 она обозначена, как ( F_{1} ).

Параллельная рукоятке часть обозначена ( F_{2} ). Она не вращает рукоятку, а сдвигает ключ либо от гайки (рис. 2а), либо в сторону гайки (рис 2б).

Рукоятка ключа – это плечо для перпендикулярной части силы.

Момент силы для рисунка 2 считаем по формуле:

[ M = F_{1} cdot d ]

Наиболее выгодно прикладывать силу перпендикулярно рукоятке (см. рис 1а). В этом случае вращательный момент силы будет наибольшим.

В остальных случаях вращать рукоятку будет не вся сила целиком, а только лишь ее перпендикулярная часть.

Помним! Между силой и ее плечом угол прямой.

Задача 1

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить часть вектора силы, вращающего гаечный ключ. С помощью этой части вектора силы рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Рисунок.

Рис. 3. Раскладываем на проекции силу, приложенную к рычагу под острым углом

Решение:

Проведем перпендикулярную ( F_{1} ) часть и параллельную рычагу ( F_{2} ) часть силы (рис. 3).

Примечание:

Чтобы разложить вектор силы на части, нужно нарисовать прямоугольник. Так, чтобы вектор, который мы раскладываем, оказался диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны рукоятке, а другие две – перпендикулярны ей.

Тогда стороны прямоугольника обозначат проекции – перпендикулярную и продольную (параллельную).

Вычислим перпендикулярную ( F_{1} ) часть силы:

[ F_{1} = F cdot sin(alpha)]

( sin(30^{o})=0,5)

( F_{1} = 20 cdot 0,5)

( F_{1} = 10 left(Hright))

Рассчитаем теперь вращательный момент M этой силы:

[ M = F_{1} cdot d ]

( M = 10 cdot 0,2 )

( M = 2 left( H cdot text{м} right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )

Раскладываем расстояние

Для подсчета вращательного момента, на проекции можно раскладывать не только силу.

На части можно разложить длину рукоятки, так, чтобы одна часть оказалась продольной силе, а другая – параллельной (рис. 4).

После выбираем часть длины, перпендикулярную силе. Эта сторона является плечом силы.

Рис. 4. Раскладываем на проекции длину рычага для приложенных под тупым (а) или острым (б) углом сил

На рисунке 4а перпендикулярно силе располагается ( d_{1} ), для этого случая момент силы считаем так:

[ M = Fcdot d_{1} ]

Из рисунка 4б выбираем перпендикулярную силе величину ( d_{2} ). Момент силы вычисляем, пользуясь формулой:

[ M = Fcdot d_{2} ]

Задача 2

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить плечо вектора приложенной силы. С помощью этого плеча рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Рис. 5. Для приложенной под острым углом силы раскладываем на проекции длину рычага

Решение:

Проведем параллельную ( d_{1} ) и перпендикулярную силе ( d_{2} ) часть рычага (рис. 5).

Примечание:

Снова рисуем прямоугольник. Но теперь не сила, а рукоятка должна оказаться диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны силе, а другие две – перпендикулярны ей.

В прямоугольнике выбираем сторону, перпендикулярную силе. Эта сторона является плечом силы.

О формулах разложения векторов на проекции подробно написано тут (откроется в новой вкладке).

Вычислим перпендикулярную силе F часть длины ( d_{2} ) рычага – плечо силы F:

[ d_{2} = d cdot sin(alpha)]

( sin(30^{o})=0,5)

( d_{2} = 0,2 cdot 0,5)

( d_{2} = 0,1 left( text{м} right))

Рассчитаем теперь с помощью найденного плеча ( d_{2} ) силы F вращательный момент M:

[ M = F cdot d_{2} ]

( M = 20 cdot 0,1 )

( M = 2 left( H cdot text{м} right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )

Расчет момента силы с помощью формулы, содержащей угол между силой и рычагом

Вращательный момент можно рассчитать без прямого указания плеча силы, зная угол между силой и рычагом. Подробнее в первой части статьи (откроется в новом окне)

Задача 3

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Не рассчитывая плеча силы найти вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Рис. 6. Рассчитаем момент приложенной под острым углом силы без разложения на проекции

Решение:

Воспользуемся формулой для вычисления вращательного момента:

[ M = F cdot d cdot sin(alpha)]

( sin(30^{o})=0,5)

( M = 20 cdot 0,2 cdot 0,5)

( M = 2 left( H cdot text{м} right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )

Как видно из задач 1 — 3, все три способа вычисления вращательного момента дают аналогичные результаты.

Источник

1. Движение по горизонтали

Сила направлена горизонтально

Пусть к бруску массой m, находящемуся на столе, приложена горизонтально направленная сила , а начальная скорость бруска ₀ направлена в ту же сторону, что и сила (рис. 20.1). Коэффициент трения между бруском и поверхностью обозначим μ.

(Здесь и далее будем подразумевать горизонтальный стол.)

(Чтобы выбрать правильное соотношение сил на чертеже, учтите, что значение коэффициента трения заключено обычно в пределах 0,2-0,5. Поэтому модуль силы трения в несколько раз меньше модуля силы нормальной реакции.)

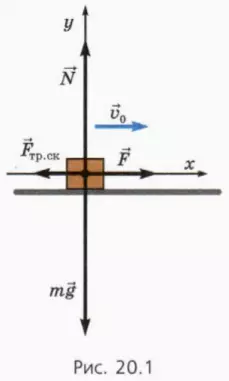
Если тело движется относительно поверхности, с которой оно соприкасается, то на него действует сила трения скольжения.

Направим оси координат, как показано на рисунке 20.1.

1. Объясните, почему справедливо уравнение

ax = F/m – μg. (1)

2. Объясните, почему из уравнения (1) следует, что:
— при F > μmg скорость тела увеличивается;
— при F < μmg скорость тела уменьшается;
— при F = μmg скорость тела не изменяется;

? 3. К бруску массой 2 кг, движущемуся по столу с начальной скоростью 3 м/с, прикладывают горизонтальную силу, равную по модулю 4 Н и направленную так же, как начальная скорость бруска. Коэффициент трения между бруском и столом равен 0,3. Какой путь пройдет брусок за 4 с?

Рассмотрим теперь случай, когда начальная скорость бруска равна нулю.

Если начальная скорость тела равна нулю, то надо выяснить, сдвинется ли оно с места. Если тело не сдвинется, то на него будет действовать сила трения искал, для которой нельзя пользоваться равенством F = μN.

? 4. Объясните, почему брусок не сдвинется с места, если

F ≤ μmg. (2)

? 5. Объясните, почему действующая на неподвижный брусок сила трения равна

F_тр = F. (3)

? 6. На столе покоится брусок массой 400 г. Коэффициент трения между бруском и столом равен 0,3. Чему будут равны ускорение бруска и действующая на него сила трения, если тянуть брусок горизонтальной силой, равной по модулю 1 Н? 2 Н?

Сила направлена вверх под углом к горизонту

К бруску приложена сила , направленная вверх под углом α к горизонту (рис. 20.2). Начальная скорость бруска равна ₀.

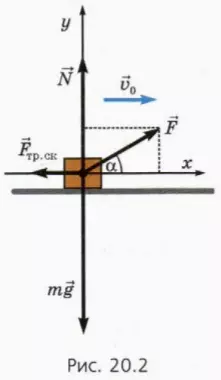
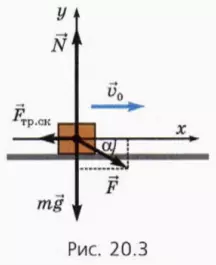
? 7. Используя рисунок 20.2, объясните смысл следующих уравнений:

? 8. К движущемуся по столу бруску массой 0,5 кг приложена сила, равная по модулю 2 Н. Коэффициент трения между бруском и столом равен 0,3. Чему равна проекция ускорения бруска на ось x, направленную по скорости бруска, если сила направлена вверх под углом к горизонту, равным:
а) 30º? б) 70º?

? 9. Чему равны модуль силы нормальной реакции N и модуль силы F при равномерном перемещении по столу бруска массой 2 кг, если коэффициент трения между бруском и столом равен 0,5, а сила направлена:
а) горизонтально?
б) вверх под углом к горизонту, равным 30º?
в) вверх под углом к горизонту, равным 70º?

Итак, когда сила направлена горизонтально, N = mg и F = μmg. Если же направлена вверх под углом к горизонту, то N < mg (сила приподнимает груз), поэтому сила трения уменьшается. Казалось бы, что по этой причине всегда выполняется условие F < μmg. Однако это не так (случай в. предыдущего задания). Ведь при увеличении угла, который составляет сила с горизонтом, уменьшается горизонтальная проекция силы.

Пусть теперь сила приложена к покоящемуся бруску.

? 10. Объясните, почему брусок сдвинется с места только при условии, что

F(cos α + μ sin α) > μmg. (5)

? 11. К покоящемуся бруску массой 2 кг приложена сила, равная по модулю 10 Н. Коэффициент трения между бруском и столом равен 0,5. Чему равно ускорение бруска, если сила направлена вверх под углом к горизонту, равным:
а) 30º? б) 60º?

? 12. Груз массой 10 кг покоится на столе. Коэффициент трения между грузом и столом равен 0,4. Чему будут равны ускорение бруска и действующая на него со стороны стола сила трения, если тянуть брусок силой, равной по модулю 40 Н и направленной вверх под углом 30º к горизонту? под углом 60º к горизонту?

Сила направлена вниз под углом к горизонту

Рассмотрим теперь случаи, когда сила направлена вниз под углом к горизонту, то есть когда брусок не тянут, а толкают.
Пусть начальная скорость бруска равна ₀ (рис. 20.3).

? 13. Объясните, почему в данном случае

Заметим, что в случае, когда

tg α ≥ 1/μ, (7)

полученное выражение для проекции ускорения будет отрицательным при любом значении F. Это означает, что при любом значении F скорость бруска будет уменьшаться. Дело в том, что чем больше сила , тем сильнее брусок прижимается к столу – а при этом увеличивается сила трения. И если выполнено неравенство (7), то сила трения растет с увеличением модуля силы быстрее, чем горизонтальная проекция этой силы.

? 14. Груз перемещают равномерно, прикладывая к нему силу 100 Н, направленную вверх под углом 45º к горизонту. Какую силу надо прикладывать, чтобы равномерно перемещать это тело силой, направленной вниз под углом 45º к горизонту? Коэффициент трения равен 0,5.

Рассмотрим теперь случай, когда брусок вначале покоился.

? 15. Объясните, почему брусок не сдвинется с места, если

F(cos α – μ sin α) ≤ mg.

Обратите внимание: в этом случае брусок невозможно сдвинуть с места, как бы велика ни была приложенная сила! В таких случаях говорят, что брусок заклинивает.

? 16. К грузу массой 10 кг, находящемуся на горизонтальной поверхности, прикладывают силу 3 кН, направленную вниз под углом 80º к горизонту. Коэффициент трения равен 0,3. Чему равна действующая на тело сила трения?
Подсказка. Проверьте, заклинит ли груз.

? 17. Груз массой 10 кг покоится на столе. Коэффициент трения между грузом и столом равен 0,2. Чему будут равны ускорение бруска и действующая на него со стороны стола сила трения, если тянуть брусок силой, равной по модулю 40 Н и направленной вниз под углом к горизонту, равным: а) 30º? б) 60º?

2. Движение по вертикали

Пусть брусок массой m прижимают к стене силой , направленной под углом α к вертикали (рис. 20.4). Коэффициент трения между бруском и стеной равен μ.

(Здесь и далее будем подразумевать вертикальную стену.)

Если начальная скорость бруска равна нулю, то есть три возможности: брусок может
— начать двигаться вверх;
— начать двигаться вниз;
— остаться в покое.

Если брусок начнет двигаться, то на него будет действовать сила трения скольжения, а если он останется в покое, то на на него будет действовать сила трения покоя.

? 18. Объясните, почему брусок будет двигаться вверх, если

F(cos α – μ sin α) > mg.

Подсказка. В таком случае на брусок действует сила трения скольжения, направленная вниз.

? 19. Объясните, почему брусок будет двигаться вниз, если

F(cos α + μ sin α) < mg.

? 20. Объясните, почему брусок останется в покое, если выполнены одновременно два неравенства:

F(cos α – μ sin α) ≤ mg и F(cos α + μ sin α) ≥ mg.

? 21.Брусок массой 1 кг прижимают к стене силой, равной по модулю 30 Н. Коэффициент трения между бруском и стеной равен 0,25. Чему равно ускорение бруска и как оно направлено, если сила направлена вверх под углом 30º к вертикали? 70º к вертикали? 80º к вертикали? 90º к вертикали (горизонтально)?
Подсказка. Выясните, начнет ли брусок двигаться. И если начнет, то в каком направлении.

Дополнительные вопросы и задания

22. Чтобы равномерно перемещать груз по столу, можно прикладывать либо силу 12 Н, направленную горизонтально, либо силу 11 Н, направленную вверх под углом 30º к горизонту.
а) Чему равны: коэффициент трения между грузом и столом? масса груза?
б) Чему равна сила нормальной реакции опоры, когда сила направлена вверх под углом 30º к горизонту?

23. Дед Мороз тянет санки массой 10 кг, на которых лежит мешок с подарками массой 20 кг. Веревка, привязанная ‘ к санкам, составляет угол 20º с горизонтом. Коэффициент трения между санками и снегом 0,2. Санки движутся равномерно со скоростью 1 м/с.
а) С какой силой Дед Мороз тянет веревку?
б) С какой силой санки давят на снег?
в) Чему равна действующая на санки сила трения?
г) С каким ускорением будут двигаться санки, если мешок с подарками упадет с ннх, а Дед Мороз будет продолжать тянуть веревку с той же силой?

24. Чтобы равномерно перемещать тело по горизонтальной поверхности, прикладывая силу, направленную вниз под углом 60º к горизонту, надо, чтобы сила была в 14 раз больше силы, направленной вверх под тем же углом к горизонту. Чему равен коэффициент трения?

25. Брусок массой 3 кг прижимают к стене силой 40 Н, направленной под углом 30º к вертикали. В начальный момент брусок покоится.
а) В каком направлении будет двигаться брусок?
б) Чему будет равно ускорение бруска, если коэффициент трения между бруском и стеной равен 0,4? 0,15?

26. С какой наименьшей горизонтальной силой надо прижимать книгу массой 400 г ладонью к стене, чтобы книга покоилась? Коэффициент трения между книгой и стеной равен 0,2, а между книгой и ладонью равен 0,3.
Подсказка. Книга не начнет скользить по стене, пока каждая из сил трения покоя, действующих на книгу (со стороны стены и ладони), не достигнет своего максимально возможного значения.

Источник

Вектор силы под углом

1. Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.

2. Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.

3. Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.

Краткая теория:

Ввиду того, что сила — вектор, вычитание сил проводится по правилам, принятым для векторов. Пусть надо вычесть силу F2 из силы F1.

Параллельным переносом начало силы F2 совмещаем с началом силы F1.

Из конца вектора F2 проводим вектор в конец вектора F1. Направление — от F2 к F1. Это и есть разность.

Разложение силы на составляющие по направлениям — операция, обратная нахождению равнодействующей. Технически она выполняется переносом направлений. Сумма составляющих должна давать исходный вектор.

Пусть задан вектор силы F. Надо разложить его на составляющие по заданным направлениям A и B.

Перенесем линии направлений A и B так, чтобы они прошли через конец вектора F. В полученной фигуре мы легко узнаем параллелограмм сил, построенный на составляющих FA и FB.

Проекции сил на оси координат можно считать частным случаем разложения на заданные направления. Оси координат, как правило, мы выбираем прямоугольными, что облегчает задачу. Проекции получают опусканием перпендикуляров на заданные оси координат. Проекции — скалярные величины, то есть они не имеют направления. Но каждой проекции приписывается знак «+» или «-«, в зависимости от направления исходного вектора относительно выбранных направлений осей.

Задан вектор силы F. Надо найти его проекции на выбранные оси прямоугольной системы координат.

Опускаем перпендикуляры на оси. Получаем проекции.

Формулы для решения:

где «альфа» — угол между вектором F и осью X.

Где «альфа» — угол между векторами

Алгоритм решения типовой задачи:

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

6. Записываем ответ.

Примеры решения:

Задача 1.

Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.

1. Кратко записываем условие задачи. Отметим, что в условии не сказано, какой вектор — уменьшаемое, а какой — вычитаемое. Поэтому разберем оба случая

а) Из первого вектора вычитается второй.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

Направление — от второго вектора к первому.

б) Из второго вектора вычитается первый

2. Изображаем условие графически.

3. Проводим графическое построение.

4,5. Проведение аналитического расчета и вычислений такое же, как и выше, но направление вектора разности — противоположное.

6. Ответ: Вектор разности в обоих случаях имеет величину 9,45 Н, направление в первом случае от второго вектора к первому, во втором случае — наоборот.

Задача 2.

Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение. Равнодействующая двух сил «T» должна уравновешивать силу «F».

4. Проводим аналитический расчет. Треугольники, на которые разделился параллелограмм сил — равносторонние, так как они равнобедренные по построению, а вектор «F» делит угол пополам, то есть угол при основании равен 60 градусам. Таким образом, каждая из сил «T» равна силе «F».

5. Подставляем величины в общее решение, вычисляем.

T=60 кг. Переводим в систему СИ. В одном килограмме 9,8 ньютона. Поэтому:

6. Ответ: Сила натяжения троса 60 кг или 591 ньютон.

Задача 3.

Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

6. Ответ: Проекция на ось абсцисс равна 129,5 ньютона, проекция на ось ординат равна 75 ньютонов.

Вращательный момент, примеры расчетов

Это вторая часть статьи о моменте силы. Первая часть находится тут (откроется в новой вкладке).

Угол между силой и рычагом отличается от прямого

Раскладываем силу

Рукоятку вращает только перпендикулярная часть силы. На рисунке 2 она обозначена, как ( F_ <1>).

Параллельная рукоятке часть обозначена ( F_ <2>). Она не вращает рукоятку, а сдвигает ключ либо от гайки (рис. 2а), либо в сторону гайки (рис 2б).

Рукоятка ключа – это плечо для перпендикулярной части силы.

Момент силы для рисунка 2 считаем по формуле:

В остальных случаях вращать рукоятку будет не вся сила целиком, а только лишь ее перпендикулярная часть.

Помним! Между силой и ее плечом угол прямой.

Задача 1

Решение:

Проведем перпендикулярную ( F_ <1>) часть и параллельную рычагу ( F_ <2>) часть силы (рис. 3).

Примечание:

Тогда стороны прямоугольника обозначат проекции – перпендикулярную и продольную (параллельную).

Вычислим перпендикулярную ( F_ <1>) часть силы:

[ F_ <1>= F cdot sin(alpha)]

( F_ <1>= 10 left(Hright))

Рассчитаем теперь вращательный момент M этой силы:

( M = 2 left( H cdot text <м>right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )

Раскладываем расстояние

Для подсчета вращательного момента, на проекции можно раскладывать не только силу.

После выбираем часть длины, перпендикулярную силе. Эта сторона является плечом силы.

На рисунке 4а перпендикулярно силе располагается ( d_ <1>), для этого случая момент силы считаем так:

Из рисунка 4б выбираем перпендикулярную силе величину ( d_ <2>). Момент силы вычисляем, пользуясь формулой:

Задача 2

Решение:

Проведем параллельную ( d_ <1>) и перпендикулярную силе ( d_ <2>) часть рычага (рис. 5).

Примечание:

В прямоугольнике выбираем сторону, перпендикулярную силе. Эта сторона является плечом силы.

О формулах разложения векторов на проекции подробно написано тут (откроется в новой вкладке).

Вычислим перпендикулярную силе F часть длины ( d_ <2>) рычага – плечо силы F:

[ d_ <2>= d cdot sin(alpha)]

( d_ <2>= 0,1 left( text <м>right))

Рассчитаем теперь с помощью найденного плеча ( d_ <2>) силы F вращательный момент M:

( M = 2 left( H cdot text <м>right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )

Расчет момента силы с помощью формулы, содержащей угол между силой и рычагом

Задача 3

Решение:

Воспользуемся формулой для вычисления вращательного момента:

[ M = F cdot d cdot sin(alpha)]

( M = 20 cdot 0,2 cdot 0,5)

( M = 2 left( H cdot text <м>right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text <м>right) )

Как видно из задач 1 — 3, все три способа вычисления вращательного момента дают аналогичные результаты.

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

направления 2 -х составляющих сил;
модуль и направление одной из составляющих сил;
модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

источники:

Вращательный момент, примеры расчетов

http://zaochnik.com/spravochnik/fizika/elementy-statiki/zakony-slozhenija-sil-v-mehanike/

Источник

2010-03-23 20:42

Решение задачи о сложении нескольких сил, направленных под углом друг к другу, начнем со случая, когда на тело действуют только две силы, не лежащие на одной прямой. В этом случае, как показывает опыт, равновесие тела невозможно; значит, равнодействующая таких сил не может равняться нулю. Например, на тело, подвешенное на нити, действует вертикально сила тяжести, и если нить (а значит, и сила натяжения нити) расположена наклонно к вертикали, то тело не остается в покое. На этом основано устройство отвеса.

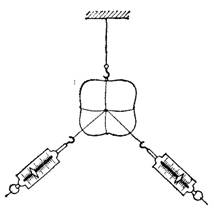
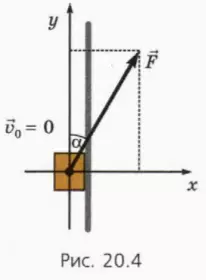
Рис. 64. Если динамометры растянуты, то равновесие груза при вертикальном положении нити невозможно

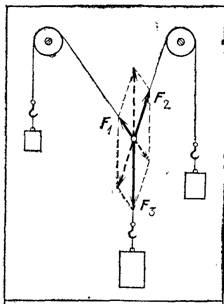
Рис. 65. Условия равновесия трех сил, действующих под углом друг к другу

Другой пример: к телу, подвешенному на нити, прикрепим два динамометра, расположенных горизонтально под углом друг к другу (рис. 64). Легко проверить на опыте, что и в этом случае тело не останется в покое и нить не будет вертикальной ни при каком растяжении динамометров.

Найдем равнодействующую двух сил, направленных под углом друг к другу. Так как равнодействующая равна по модулю и противоположна по направлению уравновешивающей силе (§ 39), то для решения задачи достаточно найти условия равновесия тела под действием трех сил (двух данных и третьей уравновешивающей). Для нахождения этих условий поставим опыт, в котором модули и направления всех сил легко определить. Свяжем три нити, привяжем к ним разные грузы и перекинем две из нитей через блоки (рис. 65). Если масса каждого из грузов меньше суммы масс двух других, то узел займет некоторое положение и будет оставаться в покое; значит, это положение будет положением равновесия. При этом все нити расположатся в одной вертикальной плоскости. На узел действуют силы, и, равные по модулю силам тяжести, действующим на грузы, и направленные вдоль нитей. Каждая из этих сил уравновешивает две остальные. Изобразим силы, приложенные к узлу, отрезками, отложенными от узла, направленными вдоль нитей и равными, в выбранном масштабе, модулям сил. Оказывается, что при равновесии отрезок, изображающий любую из этих сил, совпадает с диагональю параллелограмма, построенного на отрезках, изображающих две другие силы. Эти параллелограммы показаны на рисунке штриховыми линиями. Значит, диагональ параллелограмма изображает равнодействующую двух сил, изображаемых его сторонами, причем равнодействующая направлена в сторону, противоположную третьей силе. Таким образом, силы складываются (как и перемещения) по правилу параллелограмма, т. е. по правилу векторного сложения.

Из правила параллелограмма сил следует, что модуль равнодействующей силы зависит не только от модулей слагаемых сил, но также и от угла между их направлениями. При изменении угла модель равнодействующей изменяется в пределах от суммы модулей сил (если угол равен нулю) до разности модулей большей и меньшей сил (если угол равен 180°).
В частном случае сложения двух равных по модулю сил можно, в зависимости от угла между силами, получить любое значение модуля равнодействующей в пределах от удвоенного модуля одной из сил до нуля.

Вместо правила параллелограмма можно применять правило треугольника, как мы это делали для перемещений. При сложении более чем двух сил можно либо прибавлять их векторно одну за другой, либо строить из векторов ломаную; тогда равнодействующая изобразится звеном, замыкающим ломаную. При равновесии ломаная замкнется: равнодействующая будет равна нулю. Например, ломаная из трех уравновешивающихся сил образует треугольник.

Источник

Трение: воздействуем с силой, направленной под углом

В этой статье силу, с которой воздействуют на тело, раскладывают на проекции по координатным осям. Выбирать направления осей удобно так, чтобы раскладывать приходилось одну-две силы, то есть чтобы большинство векторов сил были бы коллинеарны осям.

Задача 1.

Коэффициент трения скольжения ящика массой 100 кг о пол равен 0,2. Ящик тянут за веревку, проходящую через его центр тяжести. Веревка образует угол с горизонтом. Какую силу надо прикладывать, чтобы ящик двигался равномерно? Какова при этом сила трения скольжения?

Введем систему координат: ось направим горизонтально, а ось — вертикально вверх. Запишем уравнения по осям по второму закону:

По оси :

Из второго уравнения найдем силу реакции опоры:

Сила трения равна

С другой стороны,

Приравняв, можем найти силу :

Определим силу трения:

Ответ: Н, Н.

Задача 2.

Тело массой 10 кг тянут по горизонтальной поверхности, прикладывая силу 50 Н, направленную под углом к горизонту. Ускорение тела равно 3,5 м/с. Найдите коэффициент трения между телом и поверхностью.

По оси :

Из второго уравнения найдем силу реакции опоры:

Сила трения равна

С другой стороны,

Приравняв, можем найти силу коэффициент трения:

Ответ: .

Задача 3.

Тело массой прижимают к потолку с силой , направленной под углом к горизонту. При этом тело неподвижно. Чему равен коэффициент трения между телом и потолком?