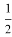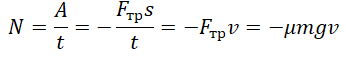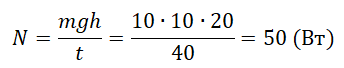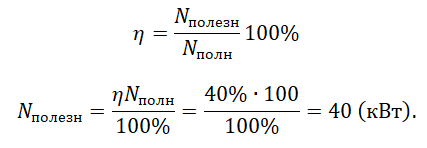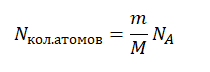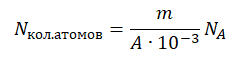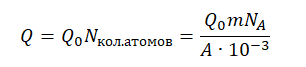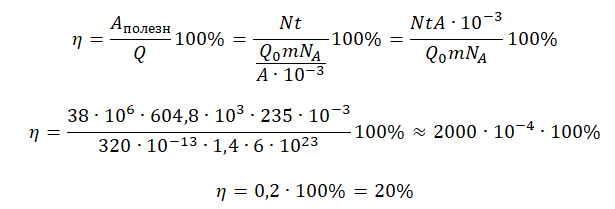Как найти силу для поднятия груза - AvtoShod.ru - решение различных проблем

На все тела в воздухе, как и в жидкости, действует выталкивающая, или архимедова сила.

Чтобы найти архимедову (выталкивающую) силу, действующую на тело в газе, надо плотность газа умножить на ускорение свободного падения ((g =) (9,8) Н/кг) и на объём тела, находящегося в газе:

FА=ρгаза⋅g⋅Vтела

Обрати внимание!

Для того чтобы летательный аппарат поднялся в воздух, необходимо, чтобы архимедова сила, действующая на шар, была больше силы тяжести.

На этом основано воздухоплавание.

Подъёмная сила воздушного шара зависит от разности архимедовой силы и силы тяжести всей конструкции.

Подъёмная сила увеличивается при увеличении архимедовой силы и уменьшении силы тяжести:
(F=F_A-F_{тяж}).

Плотность газа прямо пропорциональна силе тяжести и обратно пропорциональна подъёмной силе.

Поэтому для увеличения подъёмной силы нужно использовать газы с малой плотностью (меньшей, чем у воздуха). Одним из таких газов является водород. Однако водород взрывоопасен, поэтому его для этой цели не используют. Гелий также имеет небольшую плотность, но, в отличие от водорода, он не горюч. Это способствует тому, что многие аэростаты заполняют именно гелием.

Теплый воздух также имеет меньшую плотность, чем холодный. Поэтому и его можно использовать для создания подъёмной силы.

Чтобы управлять плотностью воздуха, используют газовые горелки. При увеличении пламени газ нагревается сильнее, его плотность уменьшается и шар поднимается выше — подъёмная сила увеличивается. Чтобы снизить высоту воздушного шара, фитиль горелки убавляют, уменьшая скорость нагрева. Воздух внутри шара охлаждается, подъёмная сила уменьшается, шар начинает опускаться вниз.

Таким образом, можно управлять высотой подъёма шара и добиться равенства силы тяжести и силы Архимеда. В этом состоянии шар повисает на одной высоте и будет перемещаться горизонтальными потоками воздуха (ветром).

Плотность атмосферного воздуха изменяется с увеличением высоты. Нагревать газ внутри шара можно до определённого значения. Поэтому при равенстве архимедовой силы и силы тяжести подъём аппарата останавливается.

Единственный выход — уменьшить силу тяжести: уменьшить массу груза. Для этого на воздушные шары берут мешки с песком, которые можно выкинуть или отсыпать часть. При уменьшении массы шара уменьшается сила тяжести, что приводит к продолжению подъёма аэростата.

Если необходимо опустить на меньшую высоту, уменьшают архимедову силу за счёт уменьшения объёма шара. Для этого открывают клапан, и часть газа из шара выходит.

Источник

Библиографическое описание:

Шумейко, А. В. Силы, действующие в простом механизме блок / А. В. Шумейко, О. Г. Веташенко. — Текст : непосредственный // Юный ученый. — 2020. — № 2 (32). — С. 38-42. — URL: https://moluch.ru/young/archive/32/1875/ (дата обращения: 25.05.2023).

В учебниках физики для 7 класса при изложении материала о подъёме груза простым механизмом блок авторы учебников рассматривают разное количество сил, действующих на блок или трос. Для выяснения, что за силы и на какие предметы они действуют в простом механизме блок при подъёме груза, и написана эта статья.

Ключевые слова:

неподвижный блок, подвижный блок, сила упругости троса, сила трения.

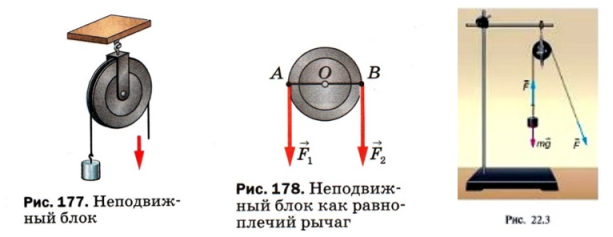
В учебнике физики для 7 класса автора А. В. Пёрышкина на рис.177 нарисован подъём груза простым механизмом неподвижный блок и на рис.178 силы

F

₁

и

F

₂

действуют на блок в точках

А

и

В

, а в учебнике О. Ф. Кабардина на рис.22.3 нарисован неподвижный блок, с тросом и сила

F

действует на трос, а сила тяжести

mg

действует на груз.

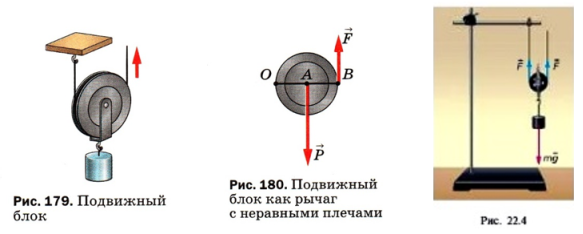
То же самое происходит и в изложении материала о подвижном блоке: в учебнике А. В. Пёрышкина рис.179, на блок действуют две силы

Р

и

F

рис.180, а в учебнике О. Ф. Кабардина на том же самом подвижном блоке три силы: сила тяжести

mg

на грузе и две силы

F

натяжения троса рис.22.4.

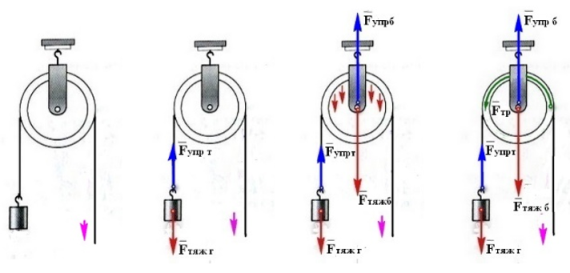
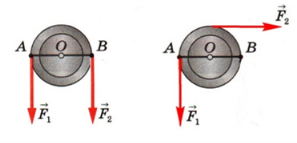
Выяснение сил, действующих в простом механизме блок, начнём с неподвижного блока, изображенного на рис.1. Груз висит на одном из концов троса, далее трос огибает верхнюю полуокружность блока и за второй конец троса происходит подъём груза. На груз действует сила притяжения Земли

F

_{тяж г}

, которая направлена вертикально вниз. Под действием силы тяжести груза в тросу возникает сила упругости

F

_{упр т}

, направленная по тросу и одинаковая по всей длине троса рис.2.

Рис.1. Рис.2. Рис.3. Рис.4.

На рис.3 трос огибает верхнюю полуокружность блока и по всей длине этой полуокружности действуют силы тяжести: груза и троса, а также сила необходимая для подъёма груза. При сложении всех этих параллельных сил равнодействующая сила тяжести

F

_{тяж б}

приложена к центру блока и направлена вертикально вниз, одновременно создавая силу упругости обоймы блока

F

_{упр б}

,

направленную по обойме блока вверх. На рис.4, при подъёме груза, трос движется по верхней полуокружности вращая блок и создавая силу трения скольжения

F

_тр

между тросом и блоком.

На рис.5 для определения силы, необходимой для поднятия груза, уберём силу тяжести блока

F

_{тяж б}

и силу упругости блока

F

_{упр б}

, так как они не влияют на величину силы поднятия груза

.

Остались три силы: сила тяжести груза

F

_{тяж г}

, сила упругости троса

F

_{упр т}

и сила трения

F

_тр

. Вспомним, что в покое или при равномерном подъёме сила упругости троса равна силе тяжести груза

F

_{упр т}

=

F

_{тяж г}

, а сила трения

F

_тр

препятствует подъёму. Поэтому для равномерного подъёма груза необходима сила

F

_п,

равная сумме сил упругости троса и силы трения

F

_п

=

F

_{упр т}

+

F

_тр

. Это равенство справедливо для поднятия груза

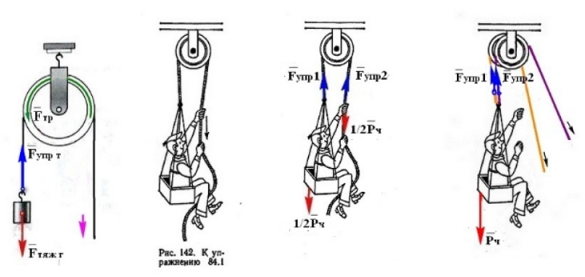
полной силой

, а на рис.142 в Элементарном учебнике физики под редакцией академика Л. Г. Ландсберга маляры и альпинисты поднимают себя

половинной силой

.

Рис. 5.Рис. 142Рис. 6Рис. 7

На рис.142 человек сидит на сидении, которое прикреплено к тросу, огибающему верхнюю часть неподвижного блока, за второй конец троса человек руками поднимает себя. На рис.6 нарисуем действующие силы подъёма человека. Земля притягивает человека, поэтому на сидение действует половина веса тела человека

Р

_ч,

вторая половина веса приходится на руки, которые производят подъём человека. Под действием деления веса человека в тросу возникают силы упругости

F

_упр

1

и

F

_упр

2

, каждая из которых будет в 2 раза меньше веса человека

F

_упр

=

Р

_ч.

Наглядно это можно представить как на рис.7, груз поднимают за два независимых троса, и вес груза разделится между тросами, и сила упругости каждого троса будет в два раза меньше веса груза.

F

_упр

=

Р

_г

.

Подведём итог по силам, действующим на неподвижном блоке:

Сила необходимая для подъёма груза на неподвижном блоке равна сумме силы упругости троса и силе трения

F

_п

=

F

_упр

+

F

_тр

.
Величина силы упругости троса зависит от способа крепления поднимаемого груза. Если груз закреплён за один из концов троса (за одну ветвь троса) то сила упругости равна весу груза

F

_упр

= Р

_г

, а если груз закреплён за оба конца троса (за две ветви троса) то сила упругости равна половине веса груза

F

_упр

=

Р

_г

. Выигрыш в

силе в 2 раза при подъёме груза

половинной силой

с

помощью неподвижного блока даёт трос, а

не неподвижный блок.
На рис.178 неподвижный блок нельзя рассматривать как равноплечий рычаг из-за того, что при изменении направления действия силы

F

₂

меняется длина рычага

ОВ

на рис.8 (видоизменённом рис.178).

Рис. 178.Рис. 8.

Рассмотрим силы, действующие на подвижный блок рис.9. Груз висит на подвижном блоке, который своей нижней полуокружностью висит на тросу, один конец этого троса закреплён, а подъём подвижного блока с грузом происходит за второй конец троса. На рис.10 обозначим действующие силы на подвижный блок: Земля притягивает груз висящий на подвижном блоке и поэтому в центре подвижного блока действует сила веса груза

Р

_г,

а на концах троса силы упругости

F

_упр

1

и

F

_упр

2

, каждая из которых в 2 раза меньше веса груза из-за того, что вес груза распределился поровну между концами (ветвями) троса, как будто груз висит на двух отдельных тросах рис.11.

Рис. 9.Рис.10.Рис.11.Рис.12.

При подъёме груза блок будет вращаться и создавать силу трения скольжения между подвижным блоком и тросом рис.12, из которого видно, что поднимая груз за один конец троса мы прикладываем силу упругости (которая в 2 раза меньше веса груза) и силу трения

F

_п

=

F

_упр

2 +

F

_тр

. Выигрыш в

силе в 2 раза даёт трос, а

не подвижный блок

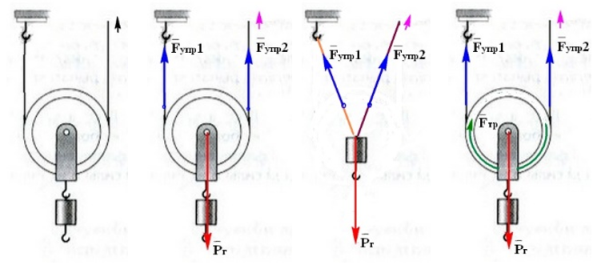
и это можно проверить с помощью рис.181 из учебника А. В. Пёрышкина, на котором нарисован неподвижный блок, который не даёт выигрыша в силе и подвижный блок — дающий выигрыш в силе в 2 раза.

Общий выигрыш в

силе этой

комбинации блоков при подъёме груза 2 раза.

Рис.181. Выигрыш в силе 2 разаРис.13 (изменённый рис.181). Выигрыш в силе 3 раза.

Если в этот рисунок добавить еще один неподвижный блок (не дающий выигрыш в силе) и закрепить конец троса за груз рис.13 (изменённый рис.181),

то выигрыш в

силе данной комбинации блоков при подъёме груза будет равен трем, потому что вес груза разделится на три части, так как висит на трёх частях (ветвях) троса.

Отсюда следует, что доказательство в учебнике А. В. Пёрышкина о том, что неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе является ошибочным, так как

выигрыш в

силе при подъёме груза на простом механизме блок даёт сила упругости троса (верёвки, цепи), а

модуль выигрыша равен количеству частей (ветвей) троса, на которых висит груз, так как вес груза делится на их количество.

Литература:

Кабардин О. Ф. Физика. 7 класс: учеб. для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1.
Ландсберг Г. С.(ред). Элементарный учебник физики, том 1. Механика. Теплота. Молекулярная физика. М. Наука 1985 г.
Пёрышкин А. В. Физика 7 кл.; учебник / А. В. Пёрышкин, — 9-е изд., пер. — М.: Дрофа, 2019, — 224 с.: ил. ISВN 978–5–358–09796–4.

Основные термины (генерируются автоматически): неподвижный блок, подъем груза, сила, вес груза, трос, конец троса, подвижной блок, подвижный блок, сила трения, сила упругости.

Источник

Простые механизмы.

Рычаг.
Неподвижный блок.
Подвижный блок.
Наклонная плоскость.
Золотое правило механики.
КПД механизма.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.

Механизм — это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.

Рычаг.

Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы $vec F_{1}$ и $vec F_{2}$ . Плечи этих сил равны соответственно $l_{1}$ и $l_{2}$ .

Условие равновесия рычага даётся правилом моментов: $F_{1} l_{1}=F_{2} l_{2}$ , откуда

$frac{displaystyle F_{displaystyle 1}}{displaystyle F_{displaystyle 2}}=frac{displaystyle l_{displaystyle 2}}{displaystyle l_{displaystyle 1}}$ .

Рис. 1. Рычаг

Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.

Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).

Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).

к оглавлению ▴

Неподвижный блок.

Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.

На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).

На правом конце нити в точке закреплён груз весом vec P . Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес vec P прило жен к точке , в которой груз крепится к нити.

К левому концу нити в точке приложена сила vec F .

Плечо силы vec F равно OA=r , где — радиус блока. Плечо веса vec P равно OB=r . Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство F=P , а во-вторых, в процессе движении груза и нити перемещение точки равно перемещению груза.

Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.

к оглавлению ▴

Подвижный блок.

На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой vec F , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити .

В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).

Вес груза vec P приложен в точке крепления груза к нити. Плечо силы vec P равно AO=r .

А вот плечо силы vec F , с которой мы тянем за нить, оказывается в два раза больше: оно равно AB=2r . Соответственно, условием равновесия груза является равенство F=P/2 (что мы и видим на рис. 3: вектор vec F в два раза короче вектора vec P ).

Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).

У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.

На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором vec F .

Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.

к оглавлению ▴

Наклонная плоскость.

Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.

В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом alpha к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом alpha «.

Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом alpha . Эта сила vec F , разумеется, направлена вдоль наклонной плоскости (рис. 5).

Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:

Проектируем на ось :

откуда

Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.

Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что F < mg , поскольку . Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол alpha .

Широко применяемыми разновидностями наклонной плоскости являются клин и винт.

к оглавлению ▴

Золотое правило механики.

Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.

Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу P/2 . Но для поднятия груза на высоту большее плечо придётся опустить на , и совершённая работа будет равна:

$A=frac{displaystyle P}{displaystyle 2}cdot 2h=Ph,$

т. е. той же величине, что и без использования рычага.

В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту над начальным положением, нам нужно пройти путь вдоль наклонной плоскости. При этом мы совершаем работу

$A=mg sin alpha frac{displaystyle h}{displaystyle sin alpha }=mgh,$

т. е. ту же самую, что и при вертикальном поднятии груза.

Данные факты служат проявлениями так называемого золотого правила механики.

Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.

Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.

к оглавлению ▴

КПД механизма.

На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.

Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.

Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.

Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:

eta =Aполезн/Аполн.

КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.

Вычислим КПД наклонной плоскости с углом alpha при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен .

Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы vec F из точки в точку на высоту (рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения vec f .

Ускорения нет, поэтому силы, действующие на груз, уравновешены:

Проектируем на ось X:

. (1)

Проектируем на ось Y:

. (2)

Кроме того,

f= mu N , (3)

Из (2) имеем:

Тогда из (3):

Подставляя это в (1), получаем:

Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:

Aполн= $F cdot PQ==mg(sin alpha+cos alpha) frac{displaystyle h}{displaystyle sin alpha}= mgh(1+ mu ctg alpha)$ .

Полезная работа, очевидно, равна:

Аполезн= mgh .

Для искомого КПД получаем:

$eta =frac{displaystyle mgh}{displaystyle mgh(1+ mu ctg alpha)}=frac{displaystyle 1}{displaystyle mu ctg alpha}.$

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Простые механизмы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Составление выражения для решения задачи

Для решения задачи необходимо воспользоваться формулой для поиска силы тяжести.

В буквенной форме ее можно записать следующим образом:

F = m * g,

Где:

F — сила тяжести объекта на поверхность Земли;
m — масса объекта (по условию задачи 20 кг);
g — постоянная гравитации или ускорение свободного падения (9,8 м/с^2).

Если подставим все известные значения в основную формулу, получим:

F = 20 * 9,8 = 196 Н.

Пренебрегая точностью значения постоянной гравитации получим 200 Ньютон.

Ответ:

Для того, чтобы поднять груз массой 20 кг понадобиться приложить силу в 200 Н.

Решение аналогичных задач

Задача №1.

Масса ребенка равна 30 кг. Какую силу должен приложить отец, чтобы поднять его на высоту 1 метр.

Решение:

Для данной задачи необходимо прибавить значение высоты.

Тогда получим:

F = 30 * 9,8 * 1 = 294 Н.

Если пренебречь значением гравитации, получим 300 Н.

Задача №2.

Определите вес груза, который давит на поверхность земли с силой 490 Н.

Решение:

Выразим значение массы из основной формулы:

m = F / g.

Получим:

m = 490 / 9,8 = 50 кг.

Источник

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

Работа силы

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Важно!

Механическая работа совершается, если:

На тело действует сила.
Под действием этой силы тело перемещается.
Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Работа силы тяжести

Модуль силы тяжести: F_тяж = mg

Работа силы тяжести: A = mgs cosα

Работа силы трения скольжения

Модуль силы трения скольжения: F_тр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Работа силы упругости

Модуль силы упругости: F_упр = kx

Работа силы упругости:

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

s = x₁ – x₂

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

Если α = 0^о, то cosα = 1.
Если 0^о < α < 90^o, то cosα > 0.
Если α = 90^о, то cosα = 0.
Если 90^о < α < 180^o, то cosα < 0.
Если α = 180^о, то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180^о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0^о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Графическое определение

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

A = S_фиг

Мощность

Определение

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела	Работа при равномерном прямолинейном движении определяется формулой: A = F_тs F_т — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
Мощность при равномерном подъеме груза	Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
Мгновенная мощность при неравномерном движении	Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
Мощность силы трения при равномерном движении по горизонтали	Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180^о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

Определения:

Работа затраченная — полная работа силы, совершенной над телом (или телом).
Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

A = Nt

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

КПД

Неподвижный блок, рычаг

A_полезн = mgh

А_{соверш.}

Наклонная плоскость

A_полезн = mgh

А_{соверш.}= Fl

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

Задание EF17557

Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?

Ответ:

а) 916 Вт

б) 3300 Вт

в) 82500 Вт

г) 297000 Вт

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать формулу для расчета мощности.

3.Выполнить общее решение задачи.

4.Подставить известные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Сила тяги, перемещающая прицеп, равна: F_т = 16,5 кН.

• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.

Переведем единицы измерения в СИ:

16,5 кН = 16,5∙10³ Н

18 км/ч = 18000/3600 м/с = 5 м/с

Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:

N=At

Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:

A = Fs

Тогда мощность равна:

N=Fst=Fv=16,5·103·5=82500 (Вт)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17574

С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Время движения	Ускорение	Модуль работы силы трения

Алгоритм решения

1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.

2.Вывести формулу для модуля работы силы трения.

3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.

Решение

При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:

x=xo+v0xt+axt22

y=yo+v0yt+ayt22

Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.

Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:

F_тр = μmg

Известно, что работа определяется формулой:

A = Fs cosα

Тогда работа силы трения равна:

A = μmgs cosα

Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:

A = μmgs

Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.

Поэтому правильная последовательность цифр в ответе: 332.

Ответ: 332

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18646

В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.

Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?

Для каждой величины определите соответствующий характер её изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Сила натяжения нити	Коэффициент трения

Алгоритм решения

Определить, какая величина изменилась во второй серии опытов.
Определить, как зависит от этой величины сила натяжения нити.
Определить, как зависит от этой величины коэффициент трения.

Решение

Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:

T = mg

Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.

Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.

Верная последовательность цифр в ответе: 13.

Ответ: 13

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18271

Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.

Алгоритм решения

1.Записать исходные данные и перевести их в СИ.

2.Записать формулу для определения КПД атомной электростанции.

3.Решить задачу в общем виде.

4.Подставить известные данные и вычислить искомую величину.

5.Массовое число: A = 235.

6.Зарядовое число: Z = 92.

Решение

Запишем исходные данные:

• Энергия, выделяемая при делении одного ядра урана-235: Q₀ = 200 МэВ.

• Масса урана-235: m = 1,4 кг.

• Время, в течение которого происходит деление: t = 1 неделя.

• Мощность атомной электростанции: N = 38 МВт.

Переведем все единицы измерения в СИ:

1 эВ = 1,6∙10^–19 Дж

200 МэВ = 200∙10⁶∙1,6∙10^–19 Дж = 320∙10^–13 Дж

1 неделя = 7∙24∙60∙60 с = 604,8∙10³с

38 МВт = 38∙10⁶ Вт

КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:

η=AполезнQ100%

Полезную работу мы можем вычислить по формуле:

A=Nt

Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.

Количество атомов равно произведению количество молей на постоянную Авогадро:

N_{кол.атомов} = νN_A

Количество молей равно отношения массы вещества к его молярной массе, следовательно:

Молярная масса численно равна массовому числу в граммах на моль. Следовательно:

M = A (г/моль) = A∙10^–3 (кг/моль)

Отсюда количество атомов равно:

Энергия, выделенная всеми атомами, равна:

Теперь можем вычислить КПД:

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 12k

Источник

Библиографическое описание:

Простые механизмы.

Рычаг.

Неподвижный блок.

Подвижный блок.

Наклонная плоскость.

Золотое правило механики.

КПД механизма.

Составление выражения для решения задачи

Решение аналогичных задач

Работа различных сил

Работа силы упругости

Работы силы трения покоя

Знак работы силы

Геометрический смысл работы

Мощность

Мощность при равномерном прямолинейном движении тела

Мощность при равномерном подъеме груза

Мгновенная мощность при неравномерном движении

Мощность силы трения при равномерном движении по горизонтали

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" width="344" height="68" src="https://spadilo.ru/wp-content/uploads/2020/08/image15-4.png" />

Коэффициент полезного действия

Устройство

Работа полезная и полная

КПД

Не пропустите также: