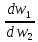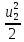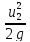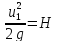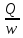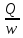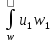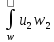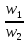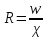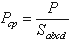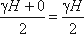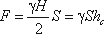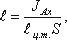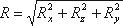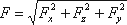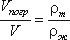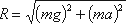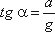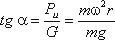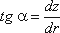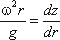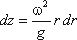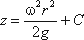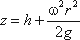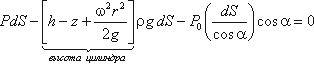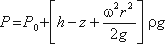Давление жидкости на плоскую наклонную стенку
Пусть
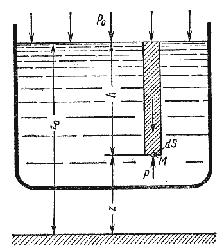
мы имеем резервуар с наклонной правой
стенкой, заполненный жидкостью с удельным
весом γ. Ширина стенки в направлении,
перпендикулярном плоскости чертежа
(от читателя), равна b
Стенка условно показана развернутой
относительно оси АВ
и заштрихована на рисунке. Построим
график изменения избыточного
гидростатического давления на стенку
АВ.
Так
как избыточное гидростатическое давление
изменяется по линейному закон P=γgh, то
для построения графика, называемого
эпюрой давления, достаточно найти
давление в двух точках, например А
и B.
Избыточное
гидростатическое давление в точке А
будет равно
PA
= γh
= γ·0 = 0
Соответственно
давление в точке В:
PB
= γh
= γH
где
H
— глубина жидкости в резервуаре.
Согласно
первому свойству гидростатического
давления, оно всегда направлено по
нормали к ограждающей поверхности.
Следовательно, гидростатическое давление
в точке В,
величина которого равна γH, надо направлять
перпендикулярно к стенке АВ.
Соединив точку А
с концом отрезка γH, получим треугольную
эпюру распределения давления АВС
с прямым углом в точке В.
Среднее
значение давления будет равно
Если
площадь наклонной стенки S=bL,
то равнодействующая гидростатического
давления равна
где
hc
= Н/2
— глубина погружения центра тяжести
плоской поверхности под уровень жидкости.
Однако
точка приложения равнодействующей
гидростатического давления ц.д. не
всегда будет совпадать с центром тяжести
плоской поверхности. Эта точка находится
на расстоянии l
от центра тяжести и равна отношению
момента инерции площадки относительно
центральной оси к статическому моменту
этой же площадки.
где
JАx
— момент инерции площади S
относительно центральной оси, параллельной
Аx.
-
Определение
силы гидростатического давления на
произвольную криволинейную поверхность.
Пусть
жидкость заполняет резервуар, правая
стенка которого представляет собой
цилиндрическую криволинейную поверхность
АВС
(рис.2.2), простирающуюся в направлении
читателя на ширину b.
Восстановим из точки А перпендикуляр
АО
к свободной поверхности жидкости. Объем
жидкости в отсеке АОСВ
находится в равновесии. Это значит, что
силы, действующие на поверхности
выделенного объема V,
и силы веса взаимно уравновешиваются.
P=
Где
Рх
–
горизонтальная составляющая, которая
равна силе давления жидкости на плоскую
вертикальную проекцию криволинейной
поверхности.
Рх=
Рc*w=(Р0+γhc)*wz
Если
P0=Pатм.,
то Pх=
γhc*wz
Рc=
Р0+γhc
–
давление
в центре тяжести вертикальной проекции.
wz
–
площадь
вертикальной проекции.(если криволинейная
поверхность цилиндрическая, то
вертикальная проекция прямоугольник;
если сферическая, то –круг или его
часть)
Рz
–
вертикальная
составляющая, которая равна весу жидкости
в объеме тела давления.
Рz
=γ*Wт.д.
Wт.д.
–
объем тела давления
Тело
давления
— фигура, ограничивающая криволинейной
поверхности вертикальную образующую,
проведенную из концов криволинейной
поверхности до уровня жидкости или его
продолжения и уровня жидкости.
Линия
действия силы Рz
всегда проходит через центр тяжести
тела давления, а вектор Рz
направлен вниз, если в теле давления
есть жидкость (т.е. «мокрое» +), Рz
направлено вверх, если в теле давления
жидкости нет (т.е. «сухое» -)
Линия
действия силы P
проходит под углом α=arttg
к горизонту через центр вращения круговой
поверхности.
-
Закон
Архимеда.
На
тело погруженное в жидкость действует
выталкивающая сила, направленная
вертикально вверх и равная весу жидкости,
в объеме погруженного в жидкость тела.
РА
=γ*W
-
Если
РА
>G,
то тело плавает на поверхности жидкости -
Если
РА
=G,
то тело плавает, в полностью или частично
погруженном состоянии. -
Если
РА
<G,
то тело тонет.
Способность
плавающего тела, выведенного из состояния
равновесия, вновь возвращаться в это
состояние называется устойчивостью.
Вес
жидкости, взятой в объеме погруженной
части судна называют водоизмещением,
а точку приложения равнодействующей
давления (т.е. центр давления) — центром
водоизмещения.
При нормальном положении судна центр
тяжести С
и центр водоизмещения d
лежат на одной вертикальной прямой
O’-O»,
представляющей ось симметрии судна и
называемой осью плавания .
Пусть
под влиянием внешних сил судно наклонилось
на некоторый угол α, часть судна KLM
вышла из жидкости, а часть K’L’M’,
наоборот, погрузилось в нее. При этом
получили новое положении центра
водоизмещения d’.
Приложим к точке d’
подъемную силу R
и линию ее действия продолжим до
пересечения с осью симметрии O’-O».
Полученная точка m
называется метацентром,
а отрезок mC
= h
называется метацентрической
высотой.
Будем считать h
положительным, если точка m
лежит выше точки C,
и отрицательным — в противном случае.
Теперь
рассмотрим условия равновесия судна:
1)
если (С выше М) h
> 0, то судно возвращается в первоначальное
положение;
2) если (С совпадает с М) h
= 0, то это случай безразличного
равновесия;
3) если (С ниже М) h<0,
то это случай неостойчивого равновесия,
при котором продолжается дальнейшее
опрокидывание судна.
Следовательно,
чем ниже расположен центр тяжести и,
чем больше метацентрическая высота,
тем больше будет остойчивость судна.
-
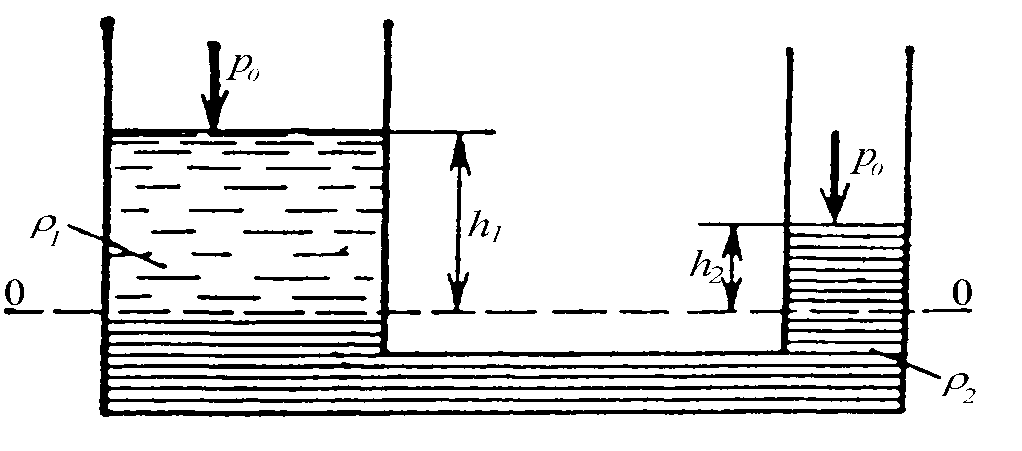
Равновесие
жидкости в сообщающихся сосудах.
Рассмотрим
равновесие жидкости в сообщающихся
сосудах. Пусть на свободной поверхности
в обоих сосудах одинаковое внешнее
давление p0. В общем
случае в сосудах разные жидкости с
плотностями р1и р2. Поверхность
раздела жидкости 0-0 является поверхностью
равного давления (z=const в однородной
жидкости). Уравнение равновесия
относительно горизонтальной плоскости
0-0 запишется в виде
При
одинаковых давлениях на свободной
поверхности высоты двух разнородных
жидкостей над плоскостью раздела обратно
пропорциональны их плотностям.
Если
в сообщающихся сосудах жидкость
однородная, то свободная поверхность
в них устанавливается на одном уровне
(h1 = h2).
-
Объяснить
следующие понятия: установившиеся и
неустановившиеся движение; траектория
и линия тока; напорное и безнапорное
движение; равномерное движение.
Виды
движения:
-
Установившиеся
— такое движение, когда скорость и
давление жидкости в точках пространства,
заполненного жидкостью -
Неустановившиеся.
U=f1(x,y,z,t)
P=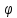
Траектория
–
путь отдельных частиц жидкости в
пространстве. Траектории могут
пересекаться, но только при неустановившемся
движении.
Линия
тока
– кривая в каждой точке, которой
направлена касательная, совпадает с
направлением вектора скорости частицы,
находящийся в данный момент времени в
этой точке. Линии тока никогда не
пересекаются!
Если
движение установившиеся, то траектория
и линии тока совпадают.
Если
сечение трубы полностью заполнено
жидкостью, то такое движение называется
напорным
движением.
Если
сечение трубы неполностью заполнено
жидкостью, т.е. есть свободная поверхность,
то такое движение называется безнапорным
движением.
Равномерное
движение —движение,
при котором тело за любые равные отрезки
времени проходит одинаковое расстояние.
Равномерное движение материальной
точки — это движение, при котором
скорость точки остаётся неизменной.
-
Вывести
уравнение неразрывности для струи.
Элементарная
струйка имеет ряд свойств:
-
Форма
элементарной струйки с течением времени
не меняется, т.к. не меняется положение
линии тока и ее образующая. -
Жидкость
из элементарной струйки не попадает в
окружающей поток и из окружающего
потока в струйку.
При
установившимся движение элементарный
расход – величина постоянная для любого
сечения трубки.
dQ=const
Предположим:
-
dQ1>
dQ2
– неверно основании 2 свойства -
dQ1<
dQ2
–
неверно на основании 2 свойства -
dQ1=
dQ2
=>
=
u1dw1=u2dw2
-
Вывод
уравнения Бернулли для элементарной
струйки жидкости.
Теорема
механики об изменение кинетической
энергии:
∆Екин=∑А
∆Екин=Екин2—
Екин1
Екин1=dm*
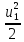
=
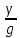
Екин1=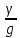
dw=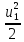
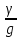
∆Екин=
γ*dw*(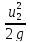
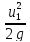
Работа
сил тяжести, давления, трения.
Ав
=dG*(Z1-Z2)=
γ*dw*(Z1-Z2)
(сила
тяжести)
Ар=dP1*dl1
– dP2*dl2=P1dw*dl1—
P2dw*dl2
=dw*(P1-P2)
(сила
давления)
dw1*dl1=dW
= γ*dw*(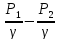
dw1*dl2=dW
В
итоге:
γ*dw*(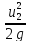
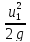
+ γ*dw*(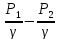
Z1+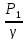
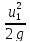
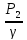
где:
Z1-удельная
потенциальная энергия положения
(геодезический напор)
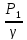
удельная
потенциальная энергия давления
(пьезометрический напор)
Z1+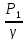
–
удельная
потенциальная энергия (гидростатический
напор)
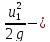
кинетическая энергия (скоростной напор)
Z1+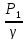
– полная
удельная энергия (гидродинамический
напор)
-
Расход
и средняя скорость по сечению потока.
Вывод уравнения неразрывности для
потока. Дать понятие смоченного периметра
и гидравлического радиуса.
Расход
потока (Q)
– объем
жидкости, протекающий через живое
сечение в единицу времени.
Q=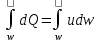
потока
Средняя
скорость(υ)—фиктивная
скорость, одинаковая для всех точек
живого сечения, при которой расход
остается тем же самым, что при истинных
скоростях.
Q=υ*w
υ=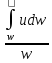
υ=
Вывод
уравнения неразрывности для потока.
u1dw1=u2dw2
Q1=Q2=const
=
u1*w1=u2*w2
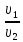
Смоченный
периметр (χ)
– периметр потока, по которому происходит
трение жидкости о стенки трубы.
Гидравлический
радиус
– отношение площади живого сечения к
смоченному периметру.
-
Вывод
уравнения Бернулли для установившегося,
плавноизменяющегося потока жидкости.
Виды существующих потерь напора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 4 мин Просмотров 12.9к.
Эта статья описывает, как правильно строить эпюру гидростатического давления. Этот материал полезен в первую очередь студентам, изучающим курс механики жидкости и газа (гидравлики).
Эпюра давления — это графическое изображение распределения гидростатического давления по стенке или по длине какого-либо контура
Содержание
- Постановка задачи
- Эпюра давления жидкости на вертикальную стенку
- Эпюра давления на наклонную стенку
- Эпюра давления на наклонную стенку + на поверхности жидкости есть избыточное давление
- Эпюра давления на криволинейную поверхность
- Эпюра двухстороннего давления, с двух сторон щита одинаковая жидкость
- Эпюра двухстороннего давления, когда с двух сторон щита находятся жидкости с разными плотностями
- Эпюра давления жидкости на стенку сложной формы, содержащую вогнутую область
Постановка задачи
Как правило, эпюру давления строят от избыточного гидростатического давления. О видах давления подробно можно прочитать в статье сайта Проводу.рф.
Построение эпюры давления заключается в расчете давления в различных точках контура (стенки), на который давит жидкость, в и откладывании этой величины давления в виде отрезка перпендикулярно контуру в определенном масштабе.
Расчет давления выполняют по формуле (основное уравнение гидростатики):
Здесь Px — избыточное давление (превышение над атмосферным), Па; ρ — плотность жидкости, кг/м3 ; g — ускорение свободного падения, g = 9,81 м/с2 ; h — глубина (высота столба жидкости над точной), м.
Далее рассмотрим различные случаи, связанные с построением эпюры гидростатического давления — от самого простого к наиболее трудному.
Эпюра давления жидкости на вертикальную стенку
Когда мы имеем дело с вертикальной плоской стенкой, нам бессмысленно считать давление в каждой точке, достаточно всего в двух: сверху в месте, где находится свободная поверхность (уровень) жидкости — точка 1, и снизу на дне, точка 2.
В данном случае избыточное давление в точке 1: p1 = 0 Па,
Избыточное давление в точке 2: p2 = ρ g H.
Эпюра давления на наклонную стенку
Практически ничем не отличается случай, когда рассматривается давление на наклонную стенку. Значение давления, рассчитанное по основному уравнению гидростатики, откладывается перпендикулярно стенке. Опять же достаточно определить давление в двух точках — сверху и снизу. Сверху, если резервуар открытый, до давление будет равно 0 Па. Снизу на дне — ρ g h.
Эпюра давления на наклонную стенку + на поверхности жидкости есть избыточное давление
Если на поверхности жидкости есть избыточное давление p0, то его величина, согласно основному уравнению гидростатики, будет добавлена во всех точках наклонной стенки. Тогда к эпюре-треугольнику добавится еще прямоугольник, ширина которого равна p0 .
Итоговая эпюра будет иметь форму трапеции.
Эпюра давления на криволинейную поверхность
Построение эпюры давления на криволинейную поверхность требует вычисления давления во многих точках этой поверхности, а значения давления откладываются по нормали к соответствующим точкам. То есть нужно выбрать несколько точек ( сколько — зависит от масштаба схемы, но чтобы была возможность изобразить по этим точкам именно криволинейную, а не ломанную линию), и вычислить в них давление по основному уравнению гидростатики.
Эпюра двухстороннего давления, с двух сторон щита одинаковая жидкость
При наличии жидкости с двух сторон щита, необходимо строить отдельно две эпюры гидростатического давления (два треугольника — слева и справа). После этого эпюра справа вычитается из большой эпюры слева, и остается трапеция, которая учитывает давление и слева, и справа.
Т.е. наличие уровня жидкости справа частично компенсирует то давление, которое создает жидкость слева.
Эпюра двухстороннего давления, когда с двух сторон щита находятся жидкости с разными плотностями
Здесь синим цветом показана эпюра для жидкости справа, которая «вырезается» из эпюры для жидкости слева. Т.е. во всех точках щита в той части, где вода находится с двух сторон, вычисляется разница давлений слева и справа. Эта разница и позволит построить результирующую эпюру давления (показана черным цветом).
Эпюра давления жидкости на стенку сложной формы, содержащую вогнутую область
Принципиально данная задача ничем не отличается от предыдущих: в каждой точке контура мы вычисляем давление и в масштабе откладываем его значение по нормали к контуру.
С точки зрения графического построения, здесь возможно поступить следующим образом:
- Сначала построить эпюру-треугольник. Он показывает, как увеличивается давление с глубиной. При этом он позволяет нам в виде отрезка получить давление в каждой точке.
- И дальше останется только перенести эти отрезки в соответствующие точки нашего контура.
- С верхней и нижней стенками при этом не должно возникнуть проблем.
- Эпюру для вогнутой области строим по принципу случая 4.
Удобнее всего будет наметить несколько точек на этом вогнутом контуре, затем провести к ним касательные линии, и отложить значение давления, посчитанное заранее или взятое из треугольника в виде отрезка, перпендикулярно этим касательным. Эффект достигнут.
2.6. Сила давления жидкости па плоскую поверхность, погружённую в жидкость
Согласно основному закону гидростатики величина давления р определяется глубиной погружения точки под уровень свободной поверхности h жидкости и величиной
плотности жидкости р.
Для горизонтальной поверхности величина давления одинакова во всех точках этой поверхности, т.к.:

Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосуда) равно произведению площади этой поверхности на величину давления на глубине погружения этой поверхности. На рисунке показан так называемый «гидравлический парадокс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов одинаковы, одинаковы и величины давлений.
Сила давления на наклонную поверхность, погруженную в жидкость. Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав-
нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ направим вдоль пересечения плоскости свободной поверхности жидкости с наклонной стенкой, а ось OZ направим вдоль этой стенки перпендикулярно оси ОХ. Тогда в качестве координатной плоскости XOZ будет выступать сама наклонная стенка. На плоскости стенки выделим малую площадку
Рекомендуемые материалы
Резервуары А и В с постоянными и одинаковыми уровнями воды соединены системой труб, приведенные длины которых L1, L2, L3, L4, а диаметры соответственно d1, d2, d3, d4. Определить: При каком избыточном давлении Р над поверхностью воды в резервуаре А р
От пункта А проложена водопроводная сеть: с последовательным и параллельным соединениями стальных, бывших в эксплуатации, трубопроводов, к двум водоемам на разных отметках и постоянной разницей уровней Н. Вода подается из одного водоема в другой поср
Для накопления энергии используется грузовой гидравлический аккумулятор (Рисунок 1), имеющий диаметр плунжера d=100мм. Определить общую массу груза от, необходимую для создания давления в цилиндре рм=2МПа а также запасаемую аккумулятором энергию при
Определить отрывающее и сдвигающее усилия и полную силу давления жидкости на полусферическую крышку радиуса R, если заданы пьезометрический напор воды Н над центром крышки и угол наклона стенки бака к горизонту (рис. 1).
На какую высоту h может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, если по нему протекает расход Q=0,004 м3/с? Диаметры d1=0,06 м, d2=0,025 м, избыточное давление в первом сечении p1=0,018 МПа. Потери нап
где: h — глубина погружения площадки относительно свободной поверхности жидкости (по вертикали).



Для определения силы давления
на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это уравнение по всей смоченной части площади стенки S .
Интеграл
оси ОХ. Он, как известно, равен произведению этой площади на координату её центра тяжести zc. Тогда окончательно:
Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тяжести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром давления.
Центр давления силы атмосферного давления p0S будет находиться в центре тяжести площадки, поскольку атмосферное давление передаётся на все точки жидкости одинаково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей
В лекции «4. Критерии основных типов ядерного наследования» также много полезной информации.
силы относительно оси ОХ будет равен сумме моментов составляющих сил относительно этой же оси.
откуда:
где:- положение центра избыточного давления на вертикальной оси,

Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по величине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления.
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 2. ОСНОВЫ ГИДРОСТАТИКИ
Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным
разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости
и их практическое применение.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.
Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних
слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
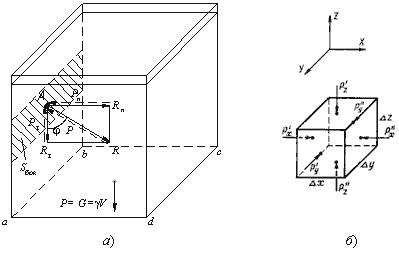
Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно
резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.
Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое
давление, действующее на дно резервуара.
Гидростатическое давление обладает свойствами.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке
касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара
площадку Sбок (заштриховано). Гидростатическое давление действует на эту площадку в виде
распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим,
что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке
А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со
стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но
противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на
два составляющих вектора: нормальный Rn (перпендикулярный к заштрихованной площадке) и
касательный Rτ к стенке.
Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления
а — первое свойство; б — второе свойство
Сила нормального давления Rn вызывает в жидкости напряжения сжатия. Этим напряжениям
жидкость легко противостоит. Сила Rτ действующая на жидкость вдоль
стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы
перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая
Rτ отсутствует. Отсюда можно сделать вывод первого свойства
гидростатического давления.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами
Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет
давить сила гидростатического давления, равная произведению соответствующего давления Px,
Py , Pz на элементарные площади. Обозначим вектора давлений,
действующие в положительном направлении (согласно указанным координатам) как P’x,
P’y, P’z, а вектора давлений, действующие в обратном направлении
соответственно P»x, P»y, P»z. Поскольку кубик
находится в равновесии, то можно записать равенства
P’xΔyΔz=P»xΔyΔz
P’yΔxΔz = P»yΔxΔz
P’zΔxΔy + γΔx, Δy, Δz = P»zΔxΔy
где γ — удельный вес жидкости;
Δx, Δy, Δz — объем кубика.
Сократив полученные равенства, найдем, что
P’x = P»x; P’y = P»y; P’z + γΔz = P»z
Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’z
и P»z, можно пренебречь и тогда окончательно
P’x = P»x; P’y = P»y; P’z=P»z
Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что
давления по различным осям одинаковы, т.е.
P’x = P»x = P’y = P»y = P’z=P»z
Это доказывает второй свойство гидростатического давления.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки
давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического
давления может быть записано в виде
P=f(x, y, z)
Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила —
сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке
рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P0
. Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на
глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на
ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного
объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь
будет внешним и направлено по нормали внутрь объема, т.е. вверх.
Рис. 2.2. Схема для вывода основного уравнения гидростатики
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS — P0 dS — ρghdS = 0
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре
объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они
перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на
dS и перегруппировав члены, найдем
P = P0 + ρgh = P0 + hγ
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой
точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления
P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев
жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее
всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами
давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем
направлениям одинаково. Это положение известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим
в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.
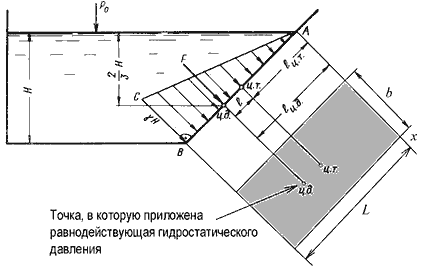
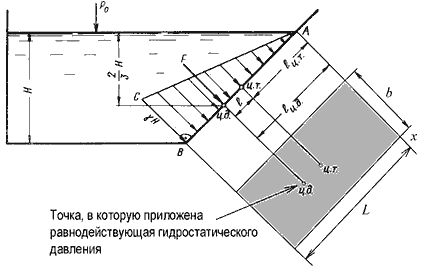
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина
стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим
график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh,
то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например
А и B.
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую
поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H — глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей
поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH,
надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом
отрезка γH, получим треугольную эпюру распределения давления АВС с прямым
углом в точке В. Среднее значение давления будет равно
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать
с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна
отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
где JАx — момент инерции площади S относительно центральной оси, параллельной
Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит
на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.
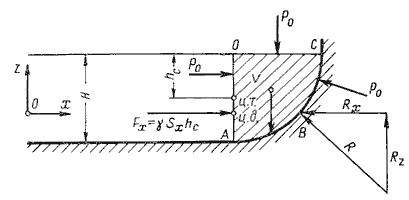
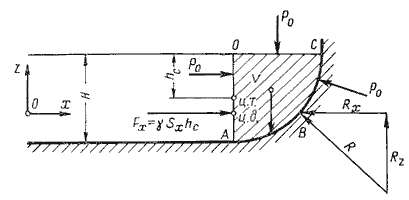
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную
поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из
точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ
находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и
силы веса взаимно уравновешиваются.
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на
цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и
жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная
стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на
плоскость yOz.
Cила гидростатического давления на площадь Sx равна Fx = γ
Sxhc.
С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка
приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на
две составляющие Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности
Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково
со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx — Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx — G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F,
то делаем вывод, что
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление,
направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
где: V — объем плавающего тела;
ρm — плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь
гидравлической сущности этой теории.
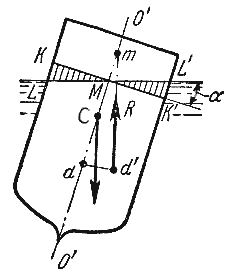
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние
называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют
водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром
водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат
на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания
(рис.2.5).
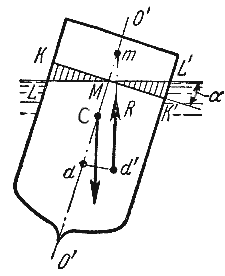
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое
положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее
действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется
метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h
положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее
опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше
будет остойчивость судна.
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью
уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы
жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость
принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
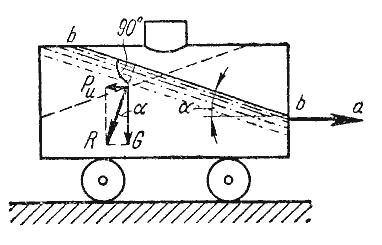
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна
движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила
инерции Pu, равная по величине ma. Равнодействующая
этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной
равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную,
составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от
ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в
цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту
под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным,
направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону
(см. рис.2.6, пунктир).
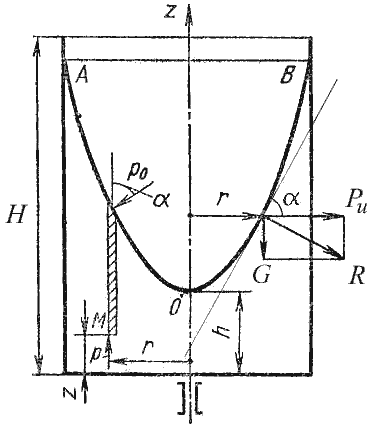
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости
во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом
случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила
тяжести G = mg и центробежная сила Pu = mω2r, где r
— расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и
представит собой параболоид вращения. Из чертежа находим
С другой стороны:
где z — координата рассматриваемой точки. Таким образом, получаем:
откуда
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем
иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму
имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим
вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS
(точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в
вертикальном направлении. С учетом уравнения (2.11) будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально
высоте z.
Проверить себя ( Тест )
Наверх страницы
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,660 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,971 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

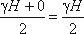
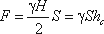
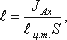
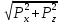

 =
=