Как найти сидерический период обращения планеты - AvtoShod.ru

Синодическим периодом обращения(S) планеты называется промежуток времени
между ее двумя последовательными
одноименными конфигурациями.

Сидерическим или звездным периодом
обращения(Т) планеты называется
промежуток времени, в течение которого
планета совершает один полный оборот
вокруг Солнца по своей орбите.

Сидерический период обращения Земли
называется звездным годом (Т_☺).
Между этими тремя периодами можно
установить простую математическую
зависимость из следующих рассуждений.
Угловое перемещение по орбите за сутки
у планеты равно,
а у Земли.
Разность суточных угловых перемещений
планеты и Земли (или Земли и планеты)
есть видимое смещение планеты за сутки,
т.е..
Отсюда для нижних планет

(2.1)

для верхних планет

(2.2)

Эти равенства называются уравнениями
синодического движения.

Непосредственно из наблюдений могут
быть определены только синодические
периоды обращений планет S и сидерический
период обращения Земли, т.е. звездный
год Т_☺. Сидерические же периоды
обращений планет Т вычисляются по
соответствующему уравнению синодического
движения.

Продолжительность звездного года равна
365,26… средних солнечных суток.

7.4. Законы Кеплера

Кеплер был сторонником учения Коперника
и поставил перед собой задачу
усовершенствовать его систему по
наблюдениям Марса, которые на протяжении
двадцати лет производил датский астроном
Тихо Браге (1546-1601) и в течение нескольких
лет — сам Кеплер.

Вначале Кеплер разделял традиционное
убеждение, что небесные тела могут
двигаться только по кругам, и поэтому
он потратил много времени на то, чтобы
подобрать для Марса круговую орбиту.

После многолетних и очень трудоемких
вычислений, отказавшись от общего
заблуждения о кругообразности движений,
Кеплер открыл три закона планетных
движений, которые в настоящее время
формулируются следующим образом:

1. Все планеты движутся по эллипсам, в
одном из фокусов которых (общем для всех
планет) находится Солнце.

2. Радиус-вектор планеты в равные
промежутки времени описывает равновеликие
площади.

3. Квадраты сидерических периодов
обращений планет вокруг Солнца
пропорциональны кубам больших полуосей
их эллиптических орбит.

Как известно, у эллипса сумма расстояний
от какой-либо его точки до двух неподвижных
точек f₁и f₂, лежащих на его
оси АП и называемых фокусами, есть
величина постоянная, равная большой
оси АП (рис. 27). Расстояние ПО (или ОA), где
О — центр эллипса, называется большой
полуосью,
а отношение— эксцентриситетом эллипса. Последний
характеризует отклонение эллипса от
окружности, у которой е = 0.

Орбиты планет мало отличаются от
окружностей, т.е. их эксцентриситеты
невелики. Наименьший эксцентриситет
имеет орбита Венеры (е = 0,007), наибольший
— орбита Плутона (е = 0,247). Эксцентриситет
земной орбиты
е = 0,017.

Согласно первому закону Кеплера Солнце
находится в одном из фокусов эллиптической
орбиты планеты. Пусть на рис. 27,а это
будет фокус f₁(С — Солнце). Тогда
наиболее близкая к Солнцу точка орбиты
П называетсяперигелием, а наиболее
удаленная от Солнца точка A —афелием.
Большая ось орбиты АП называетсялинией
апсид, а линия f₂P, соединяющая
Солнце и планету Р на ее орбите, —радиусом-вектором планеты.

Расстояние планеты от Солнца в перигелии

q = а (1 — е), (2.3)

в афелии

Q = a (l + e). (2.4)

За среднее расстояние планеты от Солнца
принимается большая полуось орбиты

Согласно второму закону Кеплера площадь
СР₁Р₂, описанная радиусом-вектором
планеты за времяt
вблизи перигелия, равна площади СР₃Р₄, описанной им за то же времяt
вблизи афелия (рис. 27, б). Так как дуга
Р₁Р₂больше дуги Р₃Р₄, то, следовательно, планета вблизи
перигелия имеет скорость большую, чем
вблизи афелия. Иными словами, ее движение
вокруг Солнца неравномерно.

Скорость движения планеты в перигелии

(2.5)

в афелии

(2.6)

где v_c— средняя или круговая
скорость планеты при r = а. Круговая
скорость Земли равна 29,78 км/сек = 29,8
км/сек.

Третий закон Кеплера записывается так:

(2.7)

где Т₁и T₂— сидерические
периоды обращений планет, а₁и a₂— большие полуоси их орбит.

Если большие полуоси орбит планет
выражать в единицах среднего расстояния
Земли от Солнца (в астрономических
единицах), а периоды обращений планет
—
в годах, то для Земли а =1 и Т = 1 и
период обращения вокруг Солнца любой
планеты

(2.8)

Соседние файлы в папке Лекции

Источник

«Небесная механика», как было принято называть науку о звездах во времена Исаака Ньютона, подчиняется классическим законам движения тел. Одними из важных характеристик этого движения являются различные периоды обращения космических объектов по своим орбитам. В статье пойдет речь о сидерическом и синодическом периодах обращения звезд, планет и их естественных спутников.

Понятие о синодическом и сидерическом временных периодах

Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.

Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.

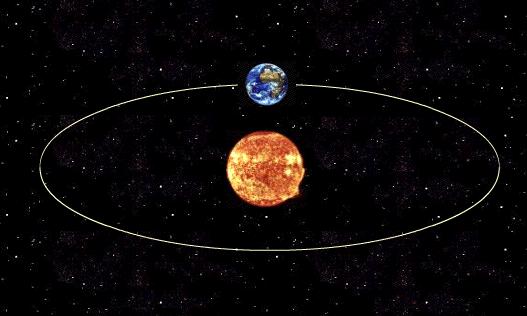
Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.

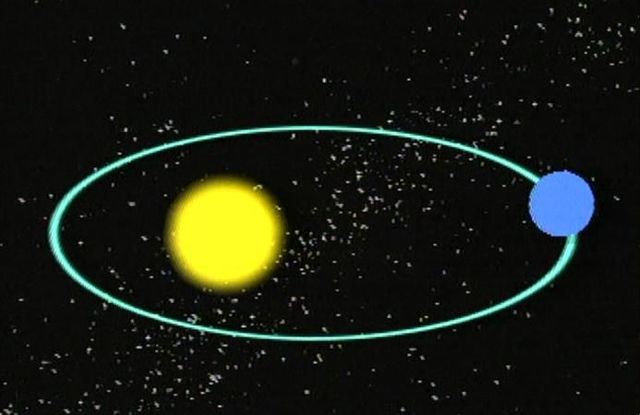
Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.

Главное отличие между сидерическим и синодическим периодами

Как уже было сказано, сидерический — это реальный период обращения, а синодический — это кажущийся, однако в чем же главная разница между этими понятиями?

Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие «сидерический период» принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период — это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.

Формула расчета сидерического периода

Для определения реального периода обращения планеты вокруг своей звезды или естественного спутника вокруг своей планеты, необходимо воспользоваться третьим законом Кеплера, который устанавливает взаимосвязь между реальным орбитальным периодом объекта и полудлиной его большой оси. В общем случае форма орбиты любого космического тела представляет собой эллипс.

Формула для определения сидерического периода имеет вид: T = 2*pi*√(a3/(G*M)), где pi = 3,14 — число пи, a — полудлина большой оси эллипса, G = 6,674*10-11 м3/(кг*с2) — универсальная гравитационная постоянная, M — масса объекта, вокруг которого осуществляется вращение.

Таким образом, зная параметры орбиты любого объекта, а также массу звезды, можно легко вычислить значение реального периода обращения этого объекта по своей орбите.

Расчет синодического временного периода

Как вычислить? Синодический период планеты или ее естественного спутника можно рассчитать, если знать значение реального ее периода обращения вокруг рассматриваемого объекта и реального периода обращения этого объекта вокруг своей звезды.

Формула, которая позволяет провести подобный расчет, имеет вид: 1/P = 1/T ± 1/S, здесь P — реальный период обращения рассматриваемого объекта, T — реальный период обращения объекта, относительно которого рассматривается движение, вокруг своей звезды, S — неизвестный синодический временной период.

Знаком «±» в формуле следует пользоваться так: если T > S, тогда формула используется со знаком «+», если же T < S, тогда нужно подставить знак «-«.

Использование формулы на примере Луны

Чтобы показать, как правильно пользоваться приведенным выражением, возьмем для примера вращение Луны вокруг Земли и синодический период обращения Луны рассчитаем.

Известно, что наша планета имеет реальный период обращения по орбите вокруг Солнца, равный T = 365,256363 дней. В свою очередь, из наблюдений можно установить, что на небосводе Луна появляется в рассматриваемой точке через каждые S = 29,530556 дня, то есть это ее синодический период. Поскольку S < T, то формулу, связывающую разные периоды, следует брать со знаком «+», получаем: 1/P = 1/365,256363 + 1/29,530556 = 0,0366, откуда P = 27,3216 дней. Как можно видеть, Луна на 2 дня быстрее совершает свой оборот вокруг Земли, чем земной наблюдатель снова может ее увидеть в отмеченном месте на небосводе.

Источник

Дисциплина
«Астрономия»

Специальность 08.02.01 «Строительство и
эксплуатация зданий и сооружений»

курс
III группа: 1с1,
2с1, 3с1, 4с1

Преподаватель:
Жданова Наталия Владимировна

ЛЕКЦИЯ
6. Конфигурации планет. (2 часа)

План
лекции:

1.
Конфигурации планет

2.
Сидерический и синодический периоды обращения планет

3.
Законы Кеплера

Конфигурациями
планет называют
характерные взаимные положения планет относительно Земли и Солнца

Конфигурации планет определяют расположение планет относительно
Земли и Солнца и обусловливают их видимость на небе. Все планеты светятся
отраженным солнечным светом, поэтому лучше всего видна та планета, которая
находится ближе к Земле, при условии, если к нам повернуто ее дневное,
освещенное Солнцем полушарие.

На рис. 4.1 изображено противостояние (ПС) Марса (М1), то есть
такая конфигурация, когда Земля находится на одной прямой между Марсом и
Солнцем. В противостоянии яркость планеты самая большая, потому что к Земле
обращено все ее дневное полушарие.

Орбиты двух планет, Меркурия и Венеры, расположены ближе к Солнцу,
чем Земля, поэтому в противостоянии они не бывают. В положении, когда Венера
или Меркурий находятся ближе всего к Земле, их не видно, потому что к нам
повернуто ночное полушарие планеты (рис. 4.1). Такая конфигурация называется
нижним соединением с Солнцем В верхнем соединении планету тоже не видно, потому
что между ней и Землей находится яркое Солнце.

Рис. 4.1. Конфигурации Венеры и Марса. Противостояние Марса —
планета находится ближе всего к Земле, ее видно всю ночь в противоположном от
Солнца направлении. Венеру лучше всего видно вечером в восточную элонгацию
слева от Солнца В₁ и утром во время западной элонгации справа
от Солнца В₂

Противостояние —
планета видна с Земли целую ночь в противоположном от Солнца направлении

Элонгация — видимое с поверхности Земли
угловое расстояние между планетой и Солнцем

Лучшие условия для наблюдения Венеры и Меркурия бывают в
конфигурациях, называемых элонгациями. Восточная элонгация — это положение,
когда планета видна вечером В₁ слева от Солнца. Западная
элонгация Венеры наблюдается утром, когда планета видна справа от Солнца в
восточной части небосклона B₂.

Условные обозначения: противостояние, планета видна всю ночь;
сообщение с Солнцем, планета не видна; восточная элонгация, планета видна
вечером в западной части горизонта; западная элонгация, планета видна утром в
восточной части небосклона.

Сидерический и синодический периоды обращения планет

Сидерический период
обращения определяет движение тел относительно звезд. Это время, за которое
планета, двигаясь по орбите, совершает полный оборот вокруг Солнца (рис. 4.2).

Рис. 4.2. Путь, соответствующий сидерическому периоду обращения
Марса вокруг Солнца, изображен пунктиром синего цвета, синодическому —
пунктиром красного цвета

Синодический период обращения
определяет движение тел относительно Земли и Солнца. Это промежуток времени, за
который наблюдаются одни и те же последовательные конфигурации планет
(противостояние, соединение, элонгация). На рис. 4.2 положения С—З₁—М₁ и
С—3₂—М₂ — два последовательных противостояния Марса.
Между синодическим S и сидерическим Т периодами обращения планеты существует
следующее соотношение: (4.1)

Законы Кеплера

Иоганн
Кеплер (рис. 4.3) определил, что Марс движется вокруг Солнца по эллипсу, а
потом было доказано, что и другие планеты имеют эллиптические орбиты.

Первый
закон Кеплера. Все планеты
обращаются вокруг Солнца по эллипсам, а Солнце находится в одном из фокусов
этих эллипсов (рис. 4.4, 4.5).

Рис. 4.4. Планеты обращаются вокруг Солнца по эллипсам. AF₁=F_min —
в перигелии; BF₁=F_max — в афелии

Главное следствие из первого закона Кеплера: расстояние между
планетой и Солнцем не остается постоянным и изменяется в пределах: r_max ≤
r ≥ r_min

Точка А орбиты, где планета приближается на наименьшее расстояние
к Солнцу, называется перигелием (греч. peri — вблизи helios — Солнце), а самую
отдаленную от центра Солнца точку В орбиты планеты назвали афелием (от греч.
аро — вдали). Сумма расстояний в перигелии и афелии равна большой оси АВ
эллипса: r_max + r_min = 2a. Большая полуось
земной орбиты (ОА или ОВ) называется астрономической единицей. 1 а. е. =
149,6×10⁶ км.

Земля
в перигелии 3—4 января приближается к Солнцу на наименьшее расстояние 147 млн
км

Земля в афелии 3—4 июля удаляется от
Солнца на самое большое расстояние 153 млн км

Второй закон Кеплера. Радиус-вектор планеты за равные промежутки времени
описывает равные площади.

Главное
следствие второго закона Кеплера состоит в том, что во время движения планеты
по орбите со временем меняется не только расстояние планеты до Солнца, но и ее
линейная и угловая скорости.

Самую
большую скорость планета имеет в перигелии, когда расстояние до Солнца
наименьшее, а самую маленькую — в афелии, когда расстояние наибольшее.

Второй
закон Кеплера фактически определяет известный физический закон сохранения
энергии: сумма кинетической и потенциальной энергии в замкнутой системе
является величиной постоянной. Кинетическая энергия определяется скоростью
планеты, а потенциальная — расстоянием между планетой и Солнцем, поэтому при
приближении к Солнцу скорость планеты возрастает (рис. 4.6).

Рис. 4.6. При приближении к Солнцу скорость планеты растет, а
при удалении — уменьшается.

Если
первый закон Кеплера проверить в условиях школы довольно трудно, ибо для этого
нужно измерить расстояние от Земли до Солнца зимой и летом, то второй закон
Кеплера может проверить любой ученик. Для этого надо убедиться, что скорость
Земли в течение года меняется. Для проверки можно использовать обычный
календарь и посчитать длительность полугодия от весеннего до осеннего
равноденствия (21.03—23.09) и, наоборот, от 23.09 до 21.03. Если бы Земля
вращалась вокруг Солнца с постоянной скоростью, то количество дней в этих
полугодиях было бы одинаковым. Но согласно второму закону Кеплера, зимой
скорость Земли больше, а летом — меньше, поэтому лето в Северном полушарии
длится чуть больше, чем зима, а в Южном полушарии, наоборот, зима немного
длиннее лета.

Максимальную
скорость Земля
имеет зимой -30,38 км/с.

Минимальную
скорость Земля
имеет летом — 29,36 км/с.

В июле Земля движется медленнее,
поэтому продолжительность лета в Северном полушарии больше, чем в Южном. Этим
объясняется, что среднегодовая температура Северного полушария Земли выше, чем
Южного

Третий закон Кеплера. Квадраты сидерических периодов обращения планет вокруг
Солнца относятся как кубы больших полуосей их орбит.

где Т₁ и
Т₂ — сидерический период обращения любых планет, и — большие
полуоси орбит этих планет.

Если
определить большую полуось орбиты какой-либо планеты или астероида, то,
согласно третьему закону Кеплера, можно вычислить период обращения этого тела,
не дожидаясь, пока оно сделает полный оборот вокруг Солнца. Например, в 1930 г.
была открыта новая планета Солнечной системы — Плутон, которая имеет большую
полуось орбиты 40 а. е., и сразу же был определен период обращения этой планеты
вокруг Солнца — 248 лет. Правда, в 2006 г., согласно постановлению съезда
Международного Астрономического Союза, Плутон перевели в статус
планет-карликов, ибо его орбита пересекает орбиту Нептуна.

Рис. 4.7. Из наблюдений была определена большая полуось
орбиты Плутона. Учитывая параметры орбиты Земли согласно 4.2, имеем Т₂ =
248 л.

Третий
закон Кеплера используется также и в космонавтике, если нужно определить период
обращения вокруг Земли спутников или космических кораблей.

Закон всемирного тяготения

Великий английский физик
и математик Исаак Ньютон доказал, что физической основой законов Кеплера
является фундаментальный закон всемирного тяготения, который не только
обусловливает движение планет в Солнечной системе, но и определяет
взаимодействие звезд в Галактике. В 1687 г. Ньютон сформулировал этот закон
так: любые два тела с массами Мum притягиваются с силой, величина которой прямо
пропорциональна произведению их масс и обратно пропорциональна квадрату
расстояния между ними (рис. 4.8):

где G — гравитационная постоянная; R — расстояние между этими
телами.

Рис. 4.8. Закон всемирного тяготения

Следует
обратить внимание, что формула (4.3) справедлива только для двух материальных
точек. Если тело имеет сферическую форму и плотность внутри распределена
симметрично относительно центра, то массу такого тела можно считать
материальной точкой, которая находится в центре сферы. Например, если
космический корабль обращается вокруг Земли, то для определения силы, с которой
корабль притягивается к Земле, принимают расстояние до центра Земли (рис. 4.9).

Рис. 4.9. Сила притяжения, действующая на космический
корабль, зависит от расстояния R+H между кораблем и центром Земли

При
помощи формулы (4.3) можно определить вес космонавтов на любой планете, если
известен ее радиус R и масса М (рис. 4.10). Закон всемирного тяготения
утверждает, что не только планета притягивается к Солнцу, но и Солнце
притягивается с такой же силой к планете, поэтому движение двух тел в
гравитационном поле происходит вокруг общего центра масс данной системы. То
есть планета не падает на Солнце, потому что она движется с определенной
скоростью по орбите, а Солнце не падает на планету под действием той же силы
тяжести, ибо оно тоже обращается вокруг общего центра масс.

Вес космонавтов зависит от массы планеты и ее радиуса. На
астероидах космонавты должны привязываться, чтобы не улететь в космическое
пространство

В
реальных условиях ни одна планета не движется по эллиптической орбите, ведь
законы Кеплера справедливы только для двух тел, обращающихся вокруг общего
центра масс. Известно, что в Солнечной системе обращаются вокруг Солнца большие
планеты и множество малых тел, поэтому каждую планету притягивает не только
Солнце — одновременно притягиваются между собой все эти тела. В результате
такого взаимодействия разных по величине и направлению сил движение каждой
планеты становится достаточно сложным. Такое движение называют возмущением.
Орбита, по которой движется при возмущенном движении планета, не является
эллипсом.

Благодаря
исследованиям возмущения орбиты планеты Уран астрономы теоретически предсказали
существование неизвестной планеты, которую в 1846 г. И. Галле обнаружил в
рассчитанном месте. Планету назвали Нептуном.

Особенность закона
всемирного тяготения заключается в том, что мы не знаем, каким образом
передается на огромное расстояние притяжение между телами. Со времени открытия
этого закона ученые придумали десятки гипотез о сути гравитационного
взаимодействия, но наши знания сегодня ненамного больше, чем во времена
Ньютона. Правда, физики открыли еще три удивительных взаимодействия между
материальными телами, которые передаются на расстоянии: электромагнитное
взаимодействие, сильное и слабое взаимодействие между элементарными частицами в
атомном ядре. Среди этих видов взаимодействия гравитационные силы являются
самыми слабыми. Например, по сравнению с электромагнитными силами
гравитационное притяжение в 10³⁹ раз слабее, но только
гравитация управляет движением планет, а также влияет на эволюцию Вселенной.
Это можно объяснить тем, что электрические заряды имеют разный знак («+» и
«-»), поэтому тела большой массы являются в основном нейтральными, и на большом
расстоянии электромагнитное взаимодействие между ними довольно слабое.

Выводы

Все
космические тела от планет до галактик движутся по закону всемирного тяготения,
который был открыт Ньютоном. Законы Кеплера определяют форму орбиты, скорость
движения планет Солнечной системы и их периоды обращения вокруг Солнца.

Тесты

Как
называется расположение планет в космическом пространстве относительно
Земли и Солнца?

А.
Конфигурация.
Б. Противостояние.

В.
Космогония.
Г. Вознесение.
Д. Перемещение.

В
противостоянии могут наблюдаться такие планеты:

А. Сатурн.
Б. Венера.
В. Меркурий.
Г. Юпитер.

В
соединении с Солнцем могут находиться такие планеты:

А. Сатурн.
Б. Венера.
В. Меркурий.
Г. Юпитер.

В
каком созвездии можно увидеть Марс во время противостояния, которое
происходит 23 сентября?

А. Лев.
Б. Козерог.
В. Орион.
Г. Рыбы.
Д. Водолей.

Как
называется точка орбиты, в которой планета находится ближе всего к Солнцу?

А. Перигелий.
Б. Перигей.
В. Апогей.
Г. Афелий.
Д. Апекс.

Когда
Марс виден на небе всю ночь?
Можно
ли увидеть Венеру в то время, когда она находится ближе всего к Земле?
В
какое время года орбитальная скорость Земли самая большая?
Почему
Меркурий трудно увидеть на небе, хотя он бывает ярче Сириуса?
Можно
ли с поверхности Марса увидеть Землю во время противостояния Марса?
Астероид
обращается вокруг Солнца с периодом 3 года. Может ли этот астероид столкнуться
с Землей, если в афелии его расстояние равно 3 а. е. от Солнца?
Может
ли существовать в Солнечной системе комета, если она в афелии проходит
возле Нептуна и обращается вокруг Солнца с периодом 100 лет?
Выведите
формулу для определения веса космонавтов на любой планете, если известны
ее радиус и масса.

Задания для наблюдений

Определите при помощи астрономического календаря, какая планета
Солнечной системы находится ближе всего к Земле в день вашего рождения в
текущем году. В каком созвездии ее можно увидеть сегодня ночью?

Ключевые понятия и термины:

Афелий,
элонгация, конфигурации планет, параллакс, перигелий, противостояние,
сидерический и синодический период.

Список
литературы:

1. Астрономия.
Базовый уровень. 11 класс: учебник / Б. А. Воронцов-Вельяминов,
Е. К. Страут. – 5-е изд., пересмотр. – М.: Дрофа, 2018.

2. Астрономия.
11 класс. Методическое пособие к учебнику Б. А. Воронцова-Вельяминова,
Е. К. Страута «Астрономия. Базовый уровень. 11 класс»/
М. А. Кунаш. — М.: Дрофа, 2018.

3.
Н.Н. Гомулина. Открытая
астрономия/ Под ред. В.Г. Сурдина. – Электронный образовательный ресурс. http://www.college.ru/astronomy/course/content/index.htm

4.
В.Г. Сурдин. Астрономические
задачи с решениями/ Издательство ЛКИ, 2017 г.

5.
Вселенная в вопросах и ответах.
Задачи и тесты по астрономии и космонавтике. В.Г. Сурдин. 2017

6. http://www.astronet.ru/

7.
https://v-kosmose.com/

Источник

Сидерический и синодический периоды обращения объектов по своим орбитам

Понятие о синодическом и сидерическом временных периодах

Главное отличие между сидерическим и синодическим периодами

Формула расчета сидерического периода

Расчет синодического временного периода

Знаком «±» в формуле следует пользоваться так: если T > S, тогда формула используется со знаком «+», если же T 19 августа, 2018

Уравнение сидерического движения для верхних планет

§ 11. К онфигурация планет. С инодический период

1. Конфигурация планет и условия их видимости

У словия видимости планет Подробные сведения о положении планет и условиях их видимости даются в «Школьном астрономическом календаре» на каждый учебный год. Эту информацию можно найти и в Интернете. меняются по-разному: если Меркурий и Венеру можно видеть только утром или вечером, то остальные — Марс, Юпитер и Сатурн — бывают видны также и ночью. По временам одна или несколько планет могут быть вовсе не видны, поскольку они располагаются на небе поблизости от Солнца. В этом случае говорят, что планета находится в соединении с Солнцем. Если же планета располагается на небе вблизи точки, диаметрально противоположной Солнцу, то она находится в противостоянии . В этом случае планета появляется над горизонтом в то время, когда Солнце заходит, а заходит она одновременно с восходом Солнца. Следовательно, всю ночь планета находится над горизонтом.

Соединение и противостояние, а также другие характерные расположения планеты относительно Солнца называются конфигурациями . Внутренние планеты (Меркурий и Венера), которые всегда находятся внутри земной орбиты, и внешние, которые движутся вне её (все остальные планеты), меняют свои конфигурации по-разному. Названия различных конфигураций внутренних и внешних планет, которые характеризуют расположение планеты относительно Солнца на небе, приведены в таблице и на рисунке 3.4.

Рис. 3.4. Конфигурации внутренней и внешней планеты

Конфигурации планет, расстояния до тел и их размеры

УРОК 7. КОНФИГУРАЦИИ ПЛАНЕТ,

РАССТОЯНИЯ ДО ТЕЛ И ИХ РАЗМЕРЫ.

1. Основные конфигурации нижних и верхних планет.

2. Сидерический и синодический периоды планет.

3. Определение размеров Земли

4. Определение расстояний до тел.

5. Определение размеров тел.

1. Основные конфигурации внутренних и внешних планет.

Сложное видимое движение планет на небесной сфере обусловлено обращением планет Солнечной системы вокруг Солнца. Само слово «планета» в переводе с древнегреческого означает «блуждающая» или «бродяга». Траектория движения небесного тела называется его орбитой.

По отношению к орбите Земли планеты разделяются на внутренние (нижние) — Меркурий, Венера, их орбиты расположены внутри земной орбиты, и внешние (верхние) — Марс, Юпитер, Сатурн, Уран, Нептун их орбиты расположены вне орбиты Земли. Внешние планеты всегда повернуты к Земле стороной, освещаемой Солнцем. Внутренние планеты меняют свои фазы подобно Луне. Плоскости орбит всех планет Солнечной системы лежат вблизи плоскости эклиптики, отклоняясь от нее менее, чем на 7°. Скорости движения планет по орбитам различны и убывают с удалением планет от Солнца. Земля движется медленнее Меркурия и Венеры, но быстрее всех остальных планет. Из-за различия скоростей движения планет в определенные моменты времени возникают различные взаимные расположения Солнца и планет.

Особые, геометрически правильные, взаимные расположения Солнца, Земли и планет называются конфигурациями. Одинаковые конфигурации планет происходят в разных точках их орбит, напротив разных созвездий, в разное время года. Конфигурации, которые создаются нижними и верхними планетами различны.

У нижних планет это соединения V1 и V3 (верхнее и нижнее) и элонгации V2 и V4 (восточная и западная). У верхних планет это – квадратуры M2 и М4 (восточная и западная), соединение M1 и противостояние M3.

Что же стоит за этими страшными названиями. Соединения — это расположение Солнца, Земли и планеты на одной прямой, при этом планета находится либо между Солнцем и Землей (нижнее соединение), либо прячется от Земли за Солнцем (верхнее соединение). Единственной конфигурацией, в которой может находиться любая, и нижняя, и верхняя планета, является верхнее соединение, при этом планету естественно нельзя наблюдать. Нижнее соединение присуще только нижним планетам, при этом, хотя и достаточно редко, мы можем наблюдать прохождение Меркурия и Венеры ( в виде черного кружка) на фоне диска Солнца.

Видимое движение нижних планет напоминает колебательное движение около Солнца. Максимальное угловое удаление нижних планет от Солнца называется элонгацией. В случае элонгации Земля планета и Солнце образуют прямоугольный треугольник, при этом в вершине прямого угла находится планета. Наибольшая элонгация Меркурия — 28˚, Венеры — 48˚. С Земли в это время видно не все освещенное Солнцем полушарие планеты, а только его часть, называемая фазой. При восточной элонгации планета видна на западе вскоре после захода Солнца, при западной – на востоке незадолго перед восходом Солнца.

Наиболее удобный момент наблюдения верхних планет – это противостояние. Все три небесных тела, как и при соединении, находятся на одной линии, но Земля в этом случае расположена между Солнцем и планетой и все полушарие планеты освещено Солнцем. Внешняя планета может находиться на любом угловом расстоянии от Солнца от 0˚ до 180˚. Когда угловое расстояние между Солнцем и верхней планетой составляет 90˚, то говорят, что планета находится в квадратуре ( квадратура – угловая четверть круга), соответственно в восточной или западной, как и при элонгации. В этом случае Земля, Солнце и планета так же образуют прямоугольный треугольник, но в вершине прямого угла находится Земля.

Система Земля — Луна — Солнце особая, в ней имеется нижнее соединение, как у внутренних планет, при этом происходит новолуние (Луна между Солнцем и Землей), и противостояние, как у внешних планет, во время полнолуния.

2. Сидерический и синодический периоды планет.

Промежуток времени, в течение которого планета совершает полный оборот вокруг Солнца по орбите, называется сидерическим (или звездным) периодом обращения планеты (Т), а промежуток времени между двумя одинаковыми конфигурациями планеты – синодическим периодом (S). Планеты движутся вокруг Солнца в одном направлении, и каждая из них через промежуток времени, равный ее сидерическому периоду, совершает один полный оборот вокруг Солнца. Пусть планеты находились в определенной конфигурации. За промежуток времени равный сидерическому периоду Земли любая нижняя планета сделает больше одного оборота вокруг Солнца и обгонит Землю, а любая верхняя — меньше полного оборота, и отстанет от Земли. Следовательно, через земной год конфигурация планет не повторится, т. е. синодический период не равен сидерическому. Однако между периодами существует зависимость, которую легко установить. Эта зависимость называется уравнением синодического движения.

Составим уравнение для нижней планеты. За земные сутки планета смещается на угол где Т – сидерический период планеты, а Земля на угол , где — сидерический период Земли. Разность этих углов даст угол опережения α, , на который нижняя планета за сутки опередит Землю. Когда за S суток накопится опережение в 360º (α·S=360º) конфигурация планет повторится. S — в данном случае — синодический период. Окончательно уравнение для нижней планеты выглядит так:

или или

Поскольку верхние планеты движутся медленнее, чем Земля, то для них уравнение принимает вид: или или

Задача. Определите период обращения Марса вокруг Солнца, зная, что противостояния Марса происходят каждые 780 суток?

;

3. Определение размеров Земли.

Представление о Земле как о шаре, который свободно без всякой опоры висит в пространстве, безусловно, является одним из величайших достижений науки древнего мира. И первое точное определение земных размеров было сделано Эратосфеном из Египта. Проделанный им эксперимент относится к одному из десяти самых красивых физических экспериментов, придуманных человечеством. Он решил измерить длину небольшой дуги земного меридиана не в градусах, а в единицах длины, и далее определить, какую часть в градусах полной окружности она составляет. Зная часть, найти длину всей окружности. Затем по длине окружности определить величину радиуса, который и является радиусом земного шара.

Очевидно, что длина дуги меридиана в градусах равна разности географических широт двух пунктов, находящихся на одном меридиане: Δφ=φв – φА. Для того чтобы определить эту разность, Эратосфен сравнил высоту Солнца в кульминации в один и тот же день в пунктах А и В ( Александрия и Асуан). В Асуане в этот день Солнце освещало дно самых глубоких колодцев, т. е. было в зените, а в Александрии отстояло от зенита на 7,2˚, Из простых геометрических построений следовало, разность широт этих городов Δφ=7,2˚. В древних единицах измерения расстояние между Александрией и Асуаном составляло 5000 греческих стадий, современное – 800 км. Обозначив длину меридиана Земли через L, имеем следующую пропорцию: откуда получаем длину меридиана равную 40000 км. Зная длину окружности, легко находим радиус Земли — 6366 км, что отличается от среднего радиуса всего на 5 км.

В какой степени форма Земли отличается от шара, выяснилось только в конце XVIII века в результате работы двух экспедиций в Южной Америке в Перу и в Скандинавии вблизи Северного полярного круга. Измерения показали, что длина в 1˚ дуги меридиана на севере и на юге больше, чем на экваторе. Это означало, что Земля сплюснута у полюсов. Ее полярный радиус на 21 км короче экваториального. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения Земли. И уже в ХХ веке выяснилось, что земной экватор также нельзя считать окружностью. Его сплюснутость в 100 раз меньше сплюснутости меридиана, но она все же существует. Точнее всего форму нашей планеты передает фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.

4. Определение расстояний до тел.

Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними, чему могут мешать естественные препятствия. Поэтому используется способ, основанный на явлении параллактического смещения. Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя. Сначала точно вычисляют длину удобно расположенного отрезка ВС, называемого базисом и двух углов В и С в треугольнике АВС. Далее по теореме синусов легко находятся значения АС и АВ. Аналогичным методом пользуются и при определении расстояния до небесных тел. Измерить расстояние от Земли до Солнца впервые удалось лишь в XVIII веке, когда был определен горизонтальный параллакс Солнца. Горизонтальным параллаксом (р) называется угол, под которым со светила, находящегося на горизонте, виден радиус Земли, перпендикулярный лучу зрения. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является радиус Земли. Единственное отличие в том, что треугольник строится прямоугольный, что упрощает вычисления.

Из треугольника OAS можно выразить величину расстояния SО=D: где RÅ – радиус Земли. Конечно, со светила никто не наблюдает радиус Земли, а горизонтальный параллакс определяют по измерениям высоты светила в момент верхней кульминации из двух точек Земли, находящихся на одном меридиане и имеющих известные широты, по аналогии с методом Эратосфена. Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны (р =57΄02΄΄), параллакс Солнца р=8,79′′. Такому значению параллакса соответствует расстояние до Солнца равное км. Это расстояние принимается за одну астрономическую единицу (1а. е.) и используется при измерении расстояний между телами Солнечной системы.

Для малых углов sinp≈p, при этом р выражен в радианах. Если р выразить в секундах, то формула примет вид: Å, так как в одном радиане 206265′′.

Методом горизонтального параллакса определяли расстояние до объектов вплоть до второй половине 20 века, когда появились новые методы определения расстояний в Солнечной системе — радиолокация и лазерная локация. С помощью этих методов были уточнены расстояния до многих тел с точностью до километра, а лазерная локация Луны позволяет определять расстояния с точностью до сантиметров.

Задача. На каком расстоянии от Земли находится Сатурн, когда его параллакс равен 0,9’’?

5. Определение размеров тел.

Зная расстояние до светила D, можно определить его линейные размеры, если измерить угловой радиус ρ. Угловой радиус это угол, под которым с Земли виден радиус тела. , Подставляя D имеем:Å, а так как углы ρ и р0 малы, то Если расстояние D известно, то , где ρ измеряется в секундах.

Задача. Чему равен диаметр Луны, если она видна с расстояния 400000 км под углом 30′? Переводим 30′ в 1800″. D =D·ρ= .

Д. з. §7. п.2,3. задачи 8,9 стр.35, § 11. задачи 1, 5, 6 стр.52.

Вопросы экспресс опроса

1. Можно ли наблюдать Меркурий по вечерам на востоке?

2. Что такое соединение?

3. Можно ли наблюдать Венеру утром на востоке, а вечером на западе?

4.Угловое расстояние планеты от Солнца равно 55°.Какая это планета, верх или ниж?

5. Что такое конфигурация?

6. Какие планеты могут пройти на фоне диска Солнца?

7. Во время каких конфигураций хорошо видны нижние планеты?

8. Во время каких конфигураций хорошо видны верхние планеты?

9. Что такое сидерический период планеты?

10. Что такое синодический период?

11. Что такое горизонтальный параллакс?

12. Что называется параллактическим смещением?

13. Когда верхняя планета находится в квадратуре?

14. Что такое элонгация?

15. При каком соединении можно наблюдать внутреннюю планету?

источники:

http://reader.lecta.rosuchebnik.ru/demo/7934-65/data/chapters/Chapter11/index.xhtml

http://pandia.ru/text/77/481/17199.php

Источник

Сегодня речь пойдет о конфигурации планет.

Конфигурация — характерное взаимное положение Солнца, планет, других небесных тел Солнечной системы на небесной сфере.

Будем называть планеты нижними, если они расположены ближе к Солнцу, чем Земля. Остальные планеты будут верхними – они расположены дальше нашей планеты от Солнца.

Планета может расположиться так, что Земля, Солнце и указанная планета находятся на одной линии. При этом может оказаться, что Солнце расположилось между Землей и рассматриваемой планетой. Такое расположение будем называть верхним соединением. Если же планета оказалась между Землей и Солнцем – то это уже нижнее соединение. Также может быть, что Земля находится между верхней планетой и Солнцем – тогда речь пойдет о противостоянии, или оппозиции.

Элонгация — одна из конфигураций планет, такое положение планеты, при котором её угловое расстояние от Солнца максимально для земного наблюдателя. Различают восточную и западную элонгацию (планета находится, соответственно, к востоку и к западу от Солнца). Об элонгации имеет смысл говорить только для Венеры и Меркурия; наилучшие условия для наблюдения этих планет наступают именно вблизи элонгаций. Из-за того, что орбиты планет не вполне круговые, угловое расстояние от Солнца в момент элонгации может быть разным, для Меркурия — от до , для Венеры — около .

Квадратура — в астрономии такая конфигурация Луны или верхней планеты (то есть планеты, более удалённой от Солнца, чем Земля) относительно Земли и Солнца, когда угол планета-Земля-Солнце равен . Если светило при этом находится к востоку от Солнца, конфигурация называется восточной квадратурой, к западу — западной квадратурой.

Сидерический период — это время совершения полного оборота какого-либо тела (планеты, кометы, астероида или искусственного спутника) вокруг главного тела (Солнца или др. планеты для спутника планеты) относительно неподвижных звёзд. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п.

Синодический же период — это время наблюдения с Земли совершения полного оборота планеты вокруг Солнца или Луны (искусственного спутника) вокруг Земли относительно Солнца ; промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.

Будем помнить также и о том, что орбиты планет не круговые. Это эллипсы, причем Солнце находится в одном из главных фокусов орбиты планеты.

Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.

Антонимом перигелия является афелий (апогелий) — наиболее удалённая от Солнца точка орбиты. Воображаемую линию между афелием и перигелием называют линией апсид.

Названия апоцентров меняются: эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:

Задача 9.

Центральное тело	Греческое название	Наименование перицентра	Наименование апоцентра
Солнце	Гелиос	перигелий	афелий
Земля	Гея	перигей	апогей
Венера	Геспер	перигесперий	апогесперий
Марс	Арес	периарий	апоарий
Сатурн	Кронос	перикроний	апокроний
Луна	Селена	периселений	апоселений

Теперь обратимся к математике и разберемся, что же такое эксцентрисистет. Будем говорить об эксцентриситете эллипса, поскольку нас пока больше интересуют орбиты планет.

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой , получаем:

Так как , то , т. е. эксцентриситет каждого эллипса меньше единицы. Заметим, что , поэтому

Или

Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение ; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности и .

Радиус перигелия рассчитывается по формуле:

где:

— большая полуось;

— эксцентриситет орбиты.

Скорость в перигелии рассчитывается по формуле:

где:

— гравитационная постоянная;

— масса Солнца;

— большая полуось;

— эксцентриситет орбиты.

Афелийное расстояние рассчитывается по формуле

Следовательно, большая полуось орбиты планеты является средним ее расстоянием от Солнца

Cидерические периоды обращения и двух планет связаны с их средними расстояниями и от Солнца третьим законом Кеплера

Если дается в годах и — в астрономических единицах, то, принимая для Земли год и а. е., получим для любой планеты

Средняя орбитальная, или круговая, скорость планеты

всегда выражается в км/с. Так как обычно задается в астрономических единицах (1 а. е.= км) и T— в годах (1 год= с), то

Подставляя , получим:

Где скорость планеты теперь выражена в км/с.

Средняя продолжительность синодического периода обращения планеты связана с сидерическим периодом уравнением синодического движения: для верхних планет

для нижних планет

где — сидерический период обращения Земли, равный 1 звездному году.

Задача 1.

Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144.

Перигельное расстояние, а.е.

афелийное расстояние, а.е.

Сидерический период обращения

а так как а. е., то планета верхняя и поэтому ее синодический период обращения вычисляется по формуле

при году:

Круговая скорость, км/с:

Задача 2.

Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е., а эксцентриситеты орбит— 0,054 и 0,008.

Перигельное расстояние Сатурна, а.е.

афелийное расстояние Сатурна, а.е.

Перигельное расстояние Нептуна, а.е.

афелийное расстояние Нептуна, а.е.

Ответ: а.е., а.е., а.е., а.е.

Задача 3.

Какая из двух планет — Нептун (а = 30,07 а.е., ) или Плутон (а = 39,52 а. е., ) — подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты планеты.

Нужно сравнить перигельные расстояния, причем для Нептуна мы его уже вычислили: а.е. Вычислим для Плутона:

Таким образом, Плутон ближе подходит к Солнцу.

Задача 4.

Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу.

Опять определим перигельные расстояния. Наибольшие расстояния от Солнца нам известны – афелийные. Тогда для Марса

Следовательно, перигельное расстояние Марса равно

Для Адониса

Следовательно, перигельное расстояние Адониса равно

Таким образом, Адонис подходит ближе к Солнцу.

Ответ: , а.е. , , а.е.

Задача 5.

На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно?

Так как афелийное расстояние у Симеизы больше, то радиус-вектор ее длиннее (абсолютно). Но, так как , то относительно радиус-вектор Икара больше изменяется.

Задача 6.

Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е.

Сидерический период Венеры равен:

Или 224,5 суток.

Сидерический период астероида Европы равен:

Ответ: сидерический период Венеры равен 0,615 года или 224,5 суток, а у Европы 5,458 года.

Задача 7.

Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно.

Определим большие полуоси орбит Аполлона и кометы Икейи:

Тогда сидерический период Аполлона

Тогда сидерический период Икейи

Ответ: года, лет.

Задача 8.

Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км?

Для спутников справедлив закон Кеплера. Применим его для Европы:

Период 42ч28м= ч.

А теперь то же самое для Ганимеда:

Ответ: Период Европы 85,23 ч, или 3^д 55, период Ганимеда 171,59 ч, или 7^д15

Задача 9.

Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4^д,518. Самый крупный спутник планеты — Титан, обращается за 15^д,945 по орбите с большой полуосью в 1221 тыс. км.

Переведем периоды в часы: период Мимаса 22,62 ч, период Реи 108,43 ч, период Титана 382, 68 ч.

Применяем закон Кеплера для Титана и Мимаса:

То же для Реи:

Ответ: большая полуось Мимаса 185,27 тыс. км, Реи 526,7 тыс. км.

Источник

7.4. Законы Кеплера

Понятие о синодическом и сидерическом временных периодах

Главное отличие между сидерическим и синодическим периодами

Формула расчета сидерического периода

Расчет синодического временного периода

Использование формулы на примере Луны

Сидерический и синодический периоды обращения планет

Законы Кеплера

Закон всемирного тяготения

Выводы

Тесты

Сидерический и синодический периоды обращения объектов по своим орбитам

Понятие о синодическом и сидерическом временных периодах

Главное отличие между сидерическим и синодическим периодами

Формула расчета сидерического периода

Расчет синодического временного периода

Уравнение сидерического движения для верхних планет

Конфигурации планет, расстояния до тел и их размеры

Не пропустите также: