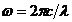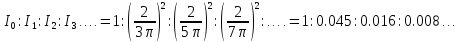В сегодняшней статье традиционно разбираем решение задач по физике. Тема: дифракция света.
Подпишитесь на наш телеграм, чтобы регулярно получать интересные новости. А если хотите поучаствовать в акции или оформить заказ со скидкой, обязательно загляните на наш второй канал для клиентов.
Дифракция: решение задач
Глупо начинать решать задачи на дифракцию, не зная, что это такое. Поэтому, сначала почитайте теорию, а уже потом приступайте к практике. Рекомендуем держать под рукой полезные формулы и руководствоваться универсальной памяткой по решению физических задач.
Кстати, дифракцию многие путают с дисперсией. Чтобы такого не случилось с вами, читайте отдельный материал в нашем блоге.
Задача на дифракцию №1
Условие
Найти расстояние между кристаллографическими плоскостями кристалла, дифракционный максимум первого порядка от которых в рентгеновских лучах с длиной волны λ = 1,5 нм наблюдается под углом 30°.
Решение
Дифракция в кристалле описывается формулой Брэгга-Вульфа:
2dsinθ=kλ
Отсюда находим искомое расстояние:
d=λ2sinθ
Вычислим:
d=1,5·10-92sin30=1,5·10-9 м
Ответ: 1.5 нм.
Задача на дифракцию №2
Условие
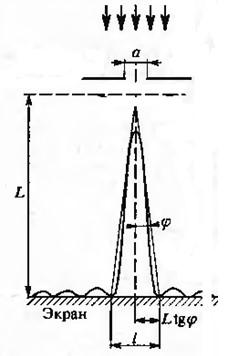
На узкую щель шириной a=2·10-4 cм падает по нормали плоская монохроматическая волна (λ=0,66 мкм). Определите ширину центрального дифракционного максимума на экране, если расстояние от щели до экрана равно L=1 м.
Решение
Ширина центрального максимума равна расстоянию между минимумами первого порядка. Эти минимумы наблюдаются под углами, которые находятся из соотношения:
asinφ=±λ
Расстояние между минимумами равно (для малых углов):
l=2Ltgφ≈2Lsinφ
Получим:
l=2Lλa
Найдем:
l=2·0,66·10-62·10-6=0,66 м
Ответ: 0.66 м.
Задача на дифракцию №3
Условие
На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки, чтобы в направлении φ=41° совпадали максимумы двух линий: λ1 = 6563 А ̇ и λ2 = 4102 А ̇?
Решение
Направление главных максимумов дифракционной решётки:
csinφ=mλ, (m=1,2,3…)
Запишем это условие для заданных длин волн и приравняем правые части:
csinφ=m1λ1csinφ=m2λ2m1λ1=m2λ2 ⇒ m2=m1λ1λ2=m165634102=1,6m1
Так как m1 и m2 целые числа, то последнее равенство справедливо при m1=5 и m2=8. Подставив m1=5 в самую первую формулу, получим:
сsinφ=5λ1c=5λ1sinφ
Произведём вычисления:
c=5·6563sin41°=50018 A≈500 нм
Ответ: c=500 нм
Задача на дифракцию №4
Условие
На экран с отверстием диаметром 2 мм падает нормально плоская волна (0,5·10-6 м). Определить, на каком расстоянии от центра отверстия находится самый дальний дифракционный минимум.
Решение
Самый дальний минимум будет наблюдаться, когда будет открыто две зоны Френеля: k=2
Для параллельного пучка света имеем:
rk=kbλ
Так как rk=d2, то:
d24=kbλb=d24kλ
Получаем:
b=2·10-324·2·5·10-7=1 м
Ответ: b=1 м.
Задача на дифракцию №5
Условие
На дифракционную решётку падает нормально свет с длиной волны 590 нм. Найти угол, под которым наблюдается максимум 6-го порядка. Период решётки 37мкм. Ответ получить в градусах.
Решение
Направление на главный максимум m-го порядка определяется выражением:
dsinφ=mλ
Отсюда:
φ=arcsinmλd
Здесь m – порядок дифракции, λ – длина волны света, d – период решетки.
Получаем:
φ=arcsin6·590·10-937·10-6=5,49°
Ответ: φ=5,49°
Нужно больше задач? Не проблема! Вот вам задачи на интерференцию света с решениями.
Вопросы на тему «Дифракция света»
Вопрос 1. Что такое дифракция?
Ответ. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д.
Вопрос 2. Приведите пример проявления дифракции из жизни.
Ответ. Звук за углом дома хорошо слышен, это потому что звуковая волна огибает дом. Это ни что иное, как проявление дифракции.
Вопрос 3. Какие есть типы дифракции?
Ответ. В зависимости от дифракционной картины различают дифракцию Фраунгофера и дифракцию Френеля.
- тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если экран и источник находятся в бесконечности. Практически применяются две линзы: в фокусе одной – источник света, а в фокусе другой – экран.
- Если преграда, на которой происходит дифракция, находится вблизи от экрана или от источника света, на котором проистекает наблюдение, то фронт дифрагированных или падающих волн имеет криволинейную поверхность (в частности, сферическую). Этот случай называется дифракцией Френеля.
Вопрос 4. Что такое дифракционная решетка?
Ответ. Дифракционная решётка представляет собой оптический прибор, действие которого основано на применении явления дифракции света. Это совокупность большого числа регулярно расположенных штрихов (выступов, щелей), нанесённых на некоторую поверхность.
При падении на решетку плоской монохроматической волны в фокальной плоскости линзы наблюдается дифракционная картина. Она является результатом двух процессов: дифракции света от каждой щели и интерференции пучков света, дифрагированных от всех щелей.
Вопрос 5. Каким проявлением природы света является дифракция?
Ответ. Дифракция – проявление волновой природы света.
Нужна помощь в решении задач и других студенческих заданий? Обращайтесь за ней в специальный студенческий сервис в любое время суток.
|
16:01 Найти ширину дифракционного максимума |
Задача по оптике. На щель шириной 0.1мм падает нормально пучок света параллельных лучей белого света (0,36-0,76) мкм. На экране отстоящем от щели на расстоянии 1 м, наблюдается дифракционная картина. Найти ширину дифракционного максимума второго порядка.
Решение задачи:Центральный максимум интенсивности света занимает область между ближайшими от него справа и слева минимумами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (рис.1) Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием
|
Категория: Решение задач по физике | Просмотров: 7509 | | Теги: ширина дифракционного максимума, минимумы интенсивности света, максимумы интенсивности света, центральный максимум, дифракция света | Рейтинг: 1.0/2 |
| Всего комментариев: 1 | |
|
Порядок вывода комментариев: |
|
Распределение интенсивности в дифракционной картине
Интенсивность
побочных max
(m=
1,2,3,…)
будет меньше интенсивности центрального
max.
Это видно из того, что с увеличением
φ ширина зоны Френеля
уменьшается, следовательно , с
увеличением угла φ
уменьшается и поток энергии в данном
направлении.
Задача
об интенсивностях в максимумах при
дифракции Фраун-гофера от одной щели
может быть решена методом графического
сложения амплитуд. Разобьем открытую
часть волновой поверхности падающей
волны на одинаковые по величине очень
узкие зоны
dx,
Амплитуда
колебаний
dE
от каждой зоны
dx
одинаковы и колебание данной зоны
отстает по фазе от колебания предыдущей
зоны на одну и ту же величину δ , зависящую
от угла φ
. При φ = 0 разность фаз соседних зон равна
0 и векторная диаграмма имеет вид,
показанный на рис.2а. Амплитуда
результирующего колебания E
равна алгебраической сумме амплитуд
складываемых колебаний. Если разность
фаз колебаний, соответствующих краям
щели равна π (что соответствует Z=1),
векторы dЕ
располагаются вдоль полуокружности
(рис.2б) длиной Е0.
Следовательно, для результирующей
амплитуды Е получаются значения
откуда
(6)
В
случае, когда bSinφ=λ
(Z=2),
колебания от краев щели отличаются
по Фазе на
2π.
Соответствующая
диаграмма изображена на рис.2в. Векторы
dE0
располагаются вдоль окружности
длиной
E0.
Результирующая амплитуда равна нулю,
т.е. имеет место первый минимум. Первый
побочный max(Z=3)
наблюдается при условии bSinφ=3λ/2.
В этом случае колебания от краев щели
отличаются по фазе на 3π.
Строя последовательно векторы dЕ
, мы обойдем полтора раза окружность
диаметром
(рис
2г). Таким образом, амплитуда Ei
первого максимума составит
2/3π
от
амплитуды E0
нулевого максимума. Учитывая, что
интенсивности света пропорциональны
квадратам амплитуд электрического
поля волны, получим:
(7)
То
есть интенсивность побочных максимумов
по сравнению с интенсивностью нулевого
максимума убывает очень быстро.
Таким
образом, центральный максимум значительно
превосходит по интенсивности остальные
максимумы; в нем сосредоточена основная
доля светового потока, прошедшего через
щель.
График
интенсивности дифракционной картины
от одной щели (без соблюдения масштаба
по вертикали) изображен на рис.3.
Ширина центрального максимума при дифракции на одной щели
Определим
ширину центрального максимума. Значения
угла φ, соответствующие краям центрального
максимума, удовлетворяют условию
первого максимума:
bSinφ1=±λ (8)
Следовательно,
угловые размеры его равны:
Δφ=2φ1=2arcSin
λ/b (9)
Линейные
размеры центрального максимума в
фокальной плоскости линзы L
определяются из условия
(10)
Подставляя
значение Sinφ1
из условия первого минимума (8) получим:
(11)
Как
видно из формулы (11), с уменьшением ширины
щели ширина центрального максимума
увеличивается и, при b→λ,
h→(бесконечность)
т.е. центральный максимум захватывает
весь экран, а освещенность экрана
спадает от центра к краям, приближаясь
к нулю.
При
увеличении ширины щели положение первых
минимумов приближается к центру картины.
Центральный максимум становится резче
и резче. При этом увеличивается его
интенсивность. При широкой щели
(b>>λ)
в центре получится ее резкое изображение.
Общее
число m
максимумов для данной щели по одну
сторону от нулевого максимума
определится из условия:
(12)
Дифракционная
решетка. Дифракция от многих щелей
Дифракционной
решеткой называется совокупность
большого числа параллельных щелей,
отстоящих друг от друга на одинаковых
расстояниях (рис. 4)
к
Суммарная
ширина темного и светлого промежутка
называется постоянной или периодом
решетки (С).
Выясним
характер дифракционной картины,
получающейся на экране при падении на
решетку перпендикулярно к ней плоской
световой волны. Каждая из щелей даст на
экране картину описываемую графиком,
изображенном на рис.3. Параллельные лучи
от всех щелей придут в одно и то же место
экрана (независимо от положения
решетки центральный максимум лежит
против центра линзы). Если бы волны,
приходящие в т. Fφ
от разных щелей, были некогерентны,
результирующая картина от N
щелей отличалась бы от картины, создаваемой
одной щелью, лишь тем, что интенсивности
всех максимумов возросли бы в N
раз. Однако, волны, идущие от различных
щелей
являются
когерентными, поэтому для нахождения
результирующей интенсивности нужно
найти фазовые соотношения между световыми
пучками, идущими от разных щелей.
Для
учета результата интерференции лучей,
идущий от разных щелей, также, как и в
случае с одной щелью, разобьем открываемую
щелями часть волновой поверхности на
узкие зоны. Амплитудное значение
напряженности электрического поля,
создаваемого в т.
Fφ
экрана
i-й
зоной, обозначим∆ Fiφ.
Тогда вектор амплитуды результирующей
волны, можно представить следующим
образом:
(13)
где
—
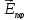
вектор напряженности электрического
поля, создаваемого в т. Fφ
n-й
щелью. Модули этих векторов одинаковы
и зависят от угла φ. Каждый следующий
вектор
повернут относительно предыдущего
—
на один и тот же угол, равный разности
фаз волн, возбуждаемых соседними щелями.
Для направлений, удовлетворяющих
условию:
∆=bsinφ=±kλ,
(k=1,
2, 3,….) (14)
все
равны
нулю. Амплитуда результирующей волны
так же будет равна нулю. Таким образом,
условие минимума для одной щели является
условием минимума и для решетки.
Если
разность хода соответственных лучей
от двух соседних щелей ∆=СSinφ
удовлетворяет условию
∆=csinφ=±mλ,
(m=1,
2, 3,….) (15)
что
соответствует разности фаз ±2πm
δ=2π=2π/λ
csinφ=±2πm
(16)
то
волны, идущие от соседних щелей взаимно
усиливают друг друга вследствие чего
амплитуда колебаний в точке экрана Fφ
будет
равна Emax=NEnφ
(17)
Формула
(15) определяет положения максимумов
интенсивности называемых главными.
Число
m
определяет порядок главного максимума.
Поскольку интенсивность пропорциональна
квадрату амплитуды волны, на основании
формулы (17).будем иметь:
Imax=N2Iφ
(18)
где
Iφ
— интенсивность в максимуме, создаваемая
лучами, идущими
под углом φ от одной щели Кроме
максимумов, определяемых условием
(15),
в промежутках между соседними главными
максимумами имеется (N-
1) вторичных минимумов, между которыми
располагаются вторичные максимумы. Эти
минимумы возникают в тех направлениях,
для которых волны идущие от соседних
щелей, гасят друг друга.
Можно
показать,
что
направление
вторичных минимумов определяется
условием:
(19)
(Здесь
К’ принимает любые целочисленные значения
кроме
0, N,
2N,…т.е.
кроме тех. при которых условие вторичных.
минимумов (19) переходит в условие
максимума (15)) Таким образом, дифракционная
картона, получающая от решетки (без
соблюдения масштаба по вертикали) имеет
вид:
Из
формулы (14)
и (15) следует, что главный максимум m-го
порядка придется на к-й. минимум, если
будет выполнено равенство:
Это
возможно, если
равно отношению целых чисел m
и k.
Тогда главный максимум m-го
порядка наложится на к-й минимум от
одной щели, максимум 2m-го
порядка на 2к-й минимум и т.д. в результате
чего главные максимумы порядков m,
2m,3m
и т.д. будут
отсутствовать.
Обычно,
отношение
.
В этом случае будут
отсутствовать все четные главные
максимумы.
Наивысший
порядок главных максимумов может быть
определен из соотношения сsinφ=mλ
при sinφ=1.
Таким образом, m≤c/λ
Ширина
центрального максимума при дифракции
на решетке
Найдем
угловую ширину δφ0
и линейные размеры h
центрального max
при дифракции от многих щелей. Положение
примыкающих к нему дополнительных
минимумов определяется условием:
(21)
Угловые
размеры центрального максимума
(22)
Линейные
размеры центрального максимума в
фокальной плоскости линзы будут равны:
то
(23)
Произведение
CN=L
есть длина дифракционной решетки.
Следовательно, угловая ширина главных
max
уменьшается с увеличением длины
решетки.
Положение
главных максимумов зависит от длины
волны λ . При освещении решетки белым
светом все максимумы, кроме центрального,
разложатся в спектр, Фиолетовый конец
которого обращен к центру дифракционной
картины, красный — наружу.
Расстояние
l
между серединой центрального максимума
и m-ным
максимумом, наблюдаемом под углом φ
, определится выражением:
(24)
Подставив
значение
,
получим
(25)
Рис.8.1
Примером оптического спектрального прибора может служить дифракционная решётка, работающая на пропускание. Данная дифракционная решётка представляет собой непрозрачный плоский экран, в котором на одинаковом расстоянии d прорезано большое число N одинаковых параллельный щелей шириной b. Расстояние d называется периодом решётки и удовлетворяет условию
d>b>>λср, (8.6)
где λср – средняя длина волны исследуемого излучения. Величины d,b и N являются основными параметрами дифракционной решётки. Полная ширина дифракционной решетки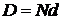 
.
Пусть на решётку нормально падает плоская монохроматическая волна
, (8.7)
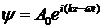
где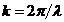
, 
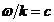
и 
-постоянная амплитуда волны. Волна частично проходит через щели, испытывая дифракцию. Многолучевая интерференция дифрагированных волн наблюдается на экране, который параллелен плоскости решётки и находится на расстоянии L от решётки в дальней зоне дифракции, где волновой параметр 
и справедливо приближение Фраунгофера (рис.8.2).
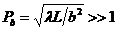
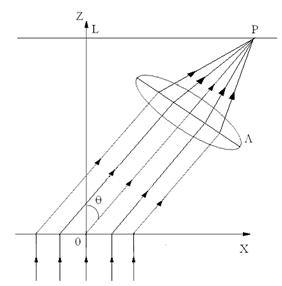
Рис.8.2
Дифрагированные волны, идущие от N щелей, фокусируются в точку наблюдения Р с помощью собирающей линзы L. Точка наблюдения Р задается углом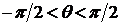 
между осью z, проходящей через центр решётки, и направлением на эту точку из центра решётки х=0. Угол θ считается положительным, если точка P находится в области x>0, и считается отрицательным, если точка P находится в области x<0.
Волновое поле на поверхности каждой щели рассматривается как вспомогательный источник вторичной волны с интенсивностью в дальней волновой зоне
, (8.9)
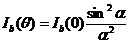
где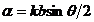 
, 
— максимальная интенсивность дифрагированной волны, идущей от одной щели в направлении нормали к плоскости решетки (
).
Разность фаз 
двух параллельных дифрагированных волн, идущих от соседних щелей под углом
, описывается формулой
, (8.10)
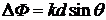
поэтому полное волновое поле в точке наблюдения Р получается путём сложения всех вторичных волн, идущих от N щелей,
. (8.11)
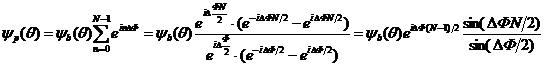
Здесь 
— волновое поле, созданное излучением от щели с наименьшим расстоянием до плоскости собирающей линзы. В (8.11) использована формула для суммы ряда, члены которого образуют геометрическую прогрессию.
Соответствующая интенсивность с учетом (8.9) определяется выражением
, (8.12)
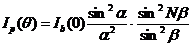
где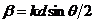
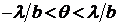
. Это угловое распределение интенсивности света, прошедшего через решетку, практически наблюдается только в пределах угловой ширины центрального дифракционного максимума 
одной щели и имеет главные максимумы, побочные максимумы и минимумы.
Главные интерференционные максимумы (спектры), где интенсивность
, (8.13)
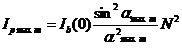
наблюдаются для углов 
удовлетворяющих уравнению
(8.14)
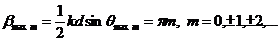
или
. (8.15)
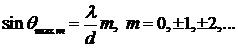
Здесь m – порядок спектра. При выполнении условия (8.15) дифрагированные волны от всех щелей приходят в точку наблюдения в фазе и возникает усиливающая интерференция.
Минимумы интенсивности, где
, (8.16)
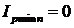
наблюдаются при 
, удовлетворяющих уравнению
(8.17)
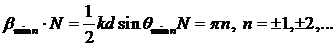
причем n≠±N, ±2N,… или
; 
. (8.18)
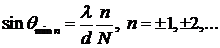
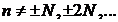
Здесь n-порядок минимума. Между двумя соседними главными максимумами находиться N-1 минимум.
Анализ выражения (8.12) показывает, что между двумя соседними минимумами интенсивности находится один побочный максимум с такой малой интенсивностью, что эти побочные максимумы практически не видны. Между двумя соседними главными максимумами всего находится N-2 побочных максимума.
График зависимости 
от 
приведен на рис 8.3. «Тонкая» структура этого распределения определяется многолучевой интерференцией дифрагированных волн, а «грубая» структура в виде огибающей главных максимумов — дифракцией на отдельной щели.
Рис.8.3
Угловая ширина главных максимумов по определению равна разности углов для двух ближайших минимумов слева и справа от главного максимума. Согласно уравнению (8.18) при условии |θ|<<1 и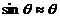 
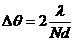
угловая ширина равна
(8.19)
и уменьшается с ростом числа щелей как 1/N.
В соответствии с приближением Фраунгофера распределение волнового поля в дальней зоне есть фурье-образ волнового поля на плоскости сразу за дифракционной решёткой. Важнейшей особенностью этого нового распределения волнового поля заключается в том, что пространственное положение главных максимумов (спектров) с m≠0 зависит от длины волны λ и соответственно частоты 
падающей на решетку плоской монохроматической волны.