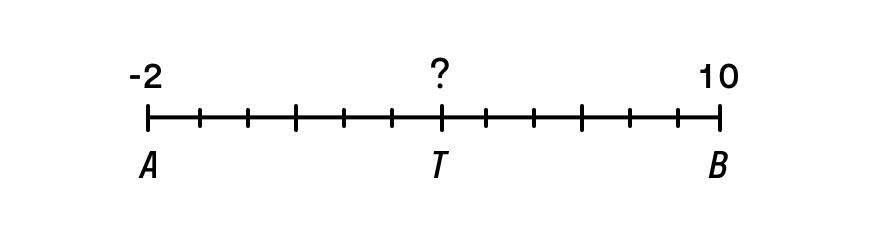Математика
5 класс
Урок №80
Представление дробей на координатном луче
Перечень рассматриваемых вопросов
– изображение дробей на координатном луче;
– запись координаты дроби;
– решение текстовых задач с опорой на смысл понятия координаты числа;
– применение дроби для выражения единиц измерения длины, массы, времени в более крупных единицах.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатная ось – это прямая, с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта.
Координата данной точки – это число, которое соответствует данной точке на координатной оси.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатным лучом.
Начало отсчёта – точка 0.
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатный луч обычно располагают горизонтально и направляют вправо.
На координатном луче можно изобразить дробь.
Изобразим дробь
Для этого единичный отрезок разделим на q частей.
Возьмём 
Точку, изображающую на координатном луче дробь p/q, называют точкой с координатой p/q или короче – точкой p/q
Например, точка А имеет координату три пятых. Пишем A (3/5).
Точка В имеет координату семь пятых, выраженную неправильной дробью или одна целая две пятых, выраженную смешанным числом. Пишем В (7/8) или В(1 2/5)
Положительные дроби называют ещё положительными рациональными числами, а точки, изображающие их на луче, называют положительными рациональными точками.
3/5, 7/5,1 2/5 – положительные дроби, или положительные рациональные числа.
Если а и с – два положительных рациональных числа и с > a, то:
- точка c на координатном луче находится правее точки а;
- расстояние между точками а и c равно c – а;
- точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с.
Докажем, что точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с:
Рассмотрим задачу.
Найдём длину отрезка, соединяющего точки:
и с = 1, и координату середины этого отрезка.
Решение
3/7 < 1, поэтому точка 1 находится правее 3/7.
Значит, длина отрезка, соединяющего точки а и с, равна:
Середина этого отрезка будет иметь координату:
Таким способом можно вычислить координату середины отрезка, соединяющего любые две рациональные точки.
Т. е. между любыми двумя рациональными точками находится ещё хотя бы одна рациональная точка.
Число (a + c) : 2 называется средним арифметическим чисел а и с.
Например:
Если необходимо вычислить среднее арифметическое нескольких чисел, нужно найти частное от деления суммы этих чисел на число слагаемых.
Например:
Рассмотрим, как применять дроби для выражения единиц измерения длины, массы и времени в более крупных единицах.
Известно, что для измерения массы используют единицы измерения: граммы, килограммы, центнеры, тонны. Если масса тела небольшая, используют г или кг. Если тело более крупное, то массу измеряют в тоннах.
Мы знаем, что 1 кг = 1000 г. А как узнать, сколько килограмм в грамме? Для этого нужно один разделить на тысячу, получим одну тысячную, т. е. в одном грамме содержится одна тысячная килограмма.
Рассмотрим единицы измерения времени. Время измеряют в секундах, минутах, часах. Вы знаете, что в одном часе шестьдесят минут, следовательно, минута будет равна одной шестидесятой часа.
Рассмотрим единицы измерения длины.
Длину измеряют в метрах, километрах, сантиметрах.
Тренировочные задания
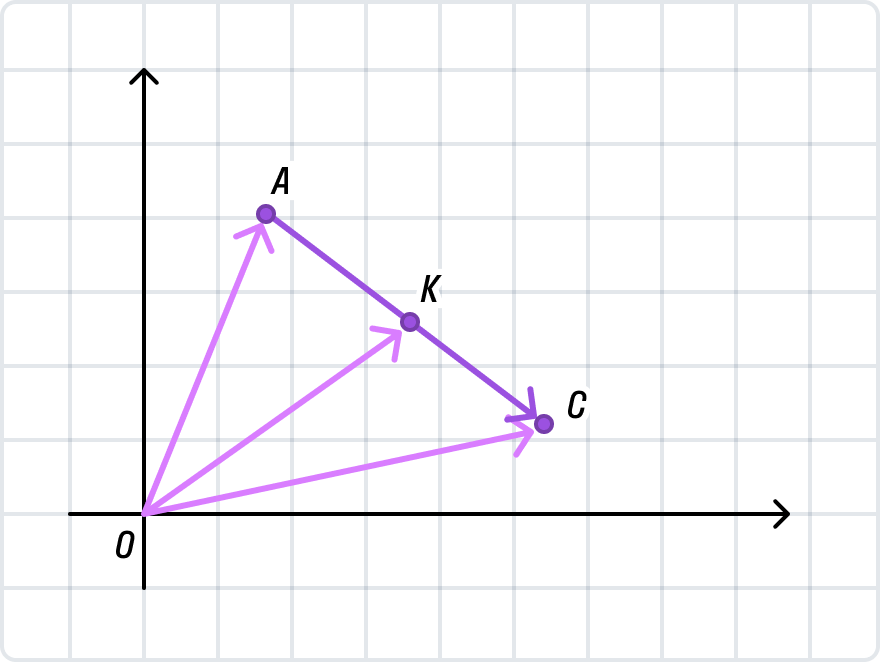
№ 1. Подставьте к изображению координаты середин отрезков АВ, ВС и СК.
Варианты ответов:
Координаты середины отрезка определяются по формуле (a + c) : 2, где а и с – координаты концов отрезка.
Найдём середину отрезка АВ. Для этого сложим координаты точки А и В, поделим на два и получим:
Значит, 1 – это середина отрезка АВ.
Найдём середину ВС. Для этого сложим координаты точки В и С, поделим на два и получим:
Значит, 2 – это середина отрезка ВС.
Найдём середину СК. Для этого сложим координаты точки С и К, поделим на два и получим:
Значит, 3 – это середина отрезка СК.
№ 2. Найдите среднее арифметическое чисел 11, 14 и 17. В ответе напишите только число: __
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
У нас три слагаемых, значит, сложим числа 11, 14 и 17 и полученную сумму разделим на 3.
(11 + 14 + 17) : 3 = 42 : 3 = 14
Правильный ответ:14.
Что такое отрезок
Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.
Отрезок — это прямая, у которой есть начало и конец, или же прямая, которая соединяет две произвольные точки, не совпадающие друг с другом.
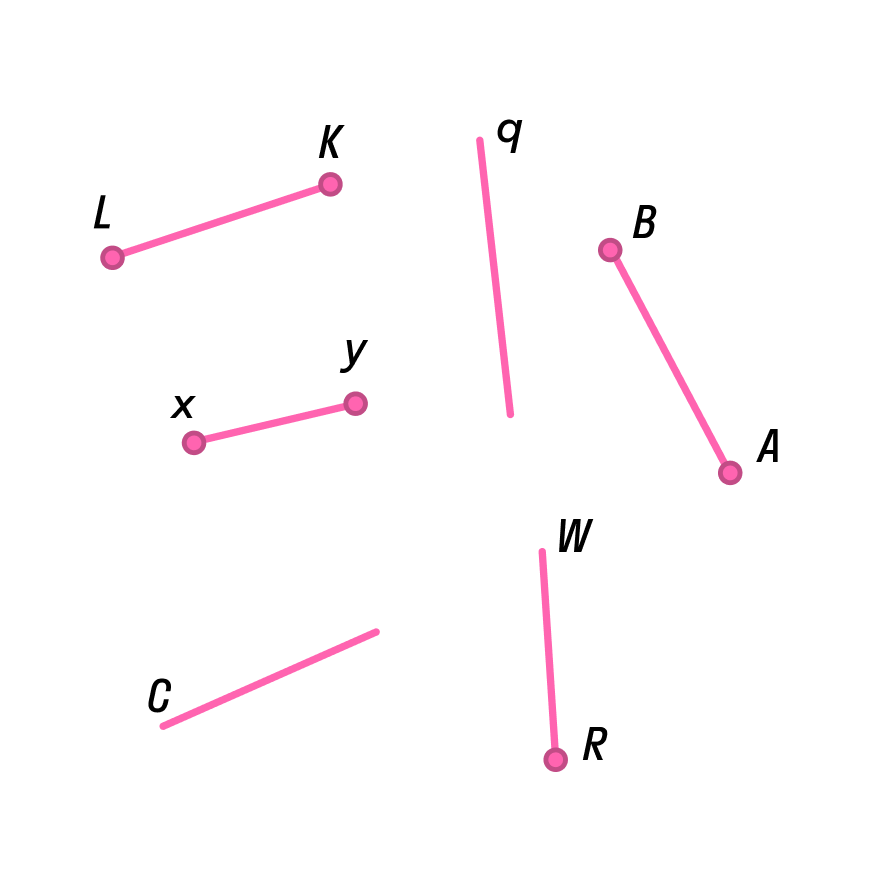
Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Что такое середина отрезка
Середина отрезка — это точка, которая находится на равном расстоянии от его концов. Иначе можно сказать так: это точка, которая делит отрезок пополам.
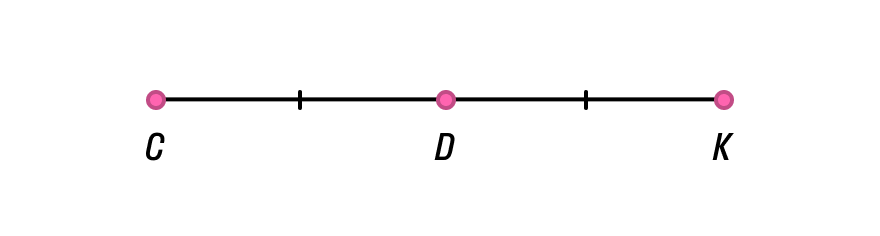
Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.
Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.
Координаты — это положение точки в пространстве.
Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.
Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!
Как найти координаты середины отрезка на координатной прямой
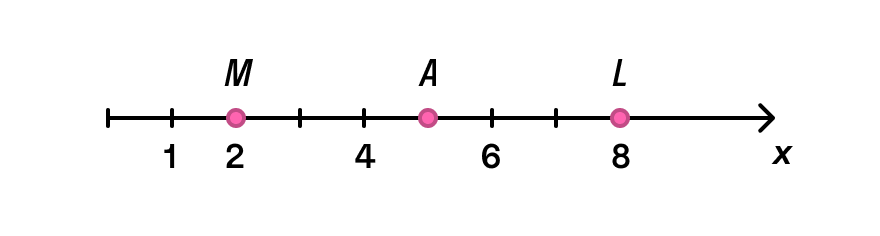
Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L. Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.
Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой XA=(XM+XL)/2 и получим:
ХА = (2 + 8)/2 = 5.
Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.
Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.
-
Точка А — это середина отрезка, а значит, MA = LA.
-
Расстояние между точками можно рассчитать через разность модулей их координат: │ХА – ХМ│=│ХL – ХА│.
-
Преобразуем правую часть, вынесем знак минуса: ХА – ХМ= — (ХА –ХL).
-
Перенесем ХА в левую часть, а все остальное — в правую: 2ХА= ХL+ ХМ.
-
Найдем ХА: ХА = (ХL + ХМ)/2.
Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.
Задача 1
Определите координаты середины отрезка АВ, если ХА = –2, ХB = 10.
Решение
Обозначим точку середины отрезка буквой Т. Тогда Хт = (ХА + ХB)/2 = (–2 + 10)/2 = 4.
Ответ: Хк = {4}.
Задача 2
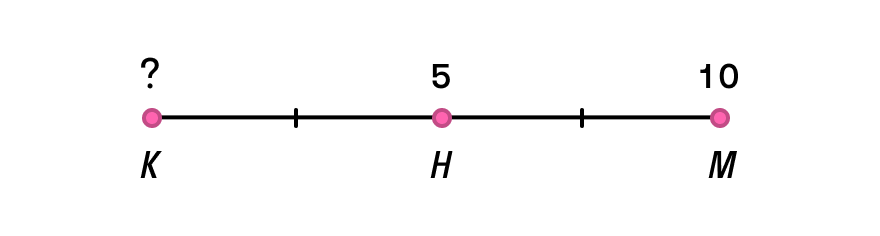
Определите координаты начала отрезка КМ с серединой в точке Н, если Хм = 5, Хн = 10.
Решение
Вначале запишем формулу для середины отрезка: Хн = (Хк + Хм)/2. Выразим Хк через нее:
Хн = (Хк + Хм)/2,
2Хн = (Хк + Хм),
2Хн – Хм = Хк,
Хк = 2Хн – Хм = 2 * 5 – 10 = 0.
Ответ: Хк = {0}
Как найти середину отрезка на плоскости
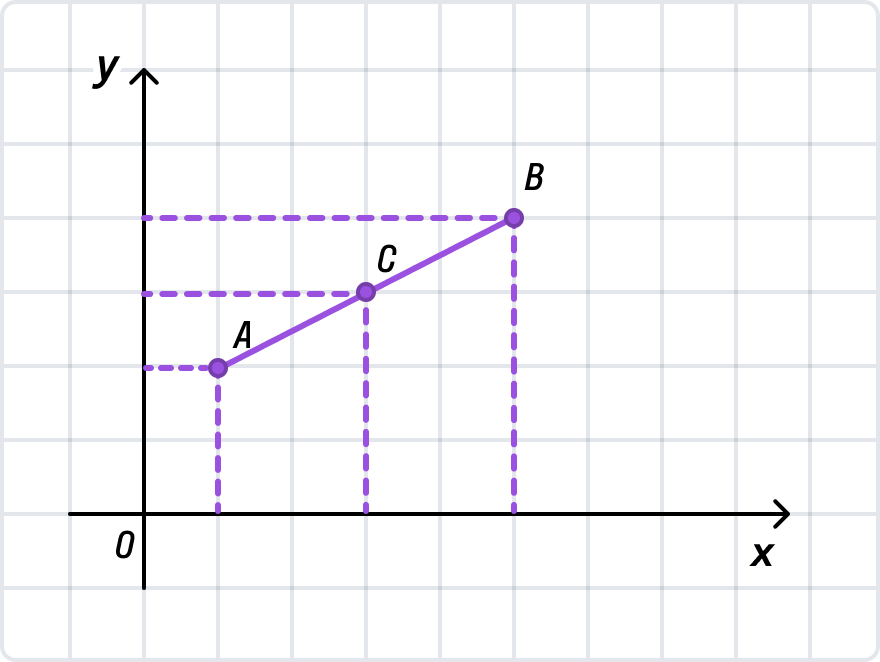
В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.
Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Хс:
Хс = (ХА + ХB)/2 = (1 + 3)/2 = 2.
Тогда УC = (УA + УB)/2 = (3 + 6)/2 = 4,5. Значит С (2; 4,5).
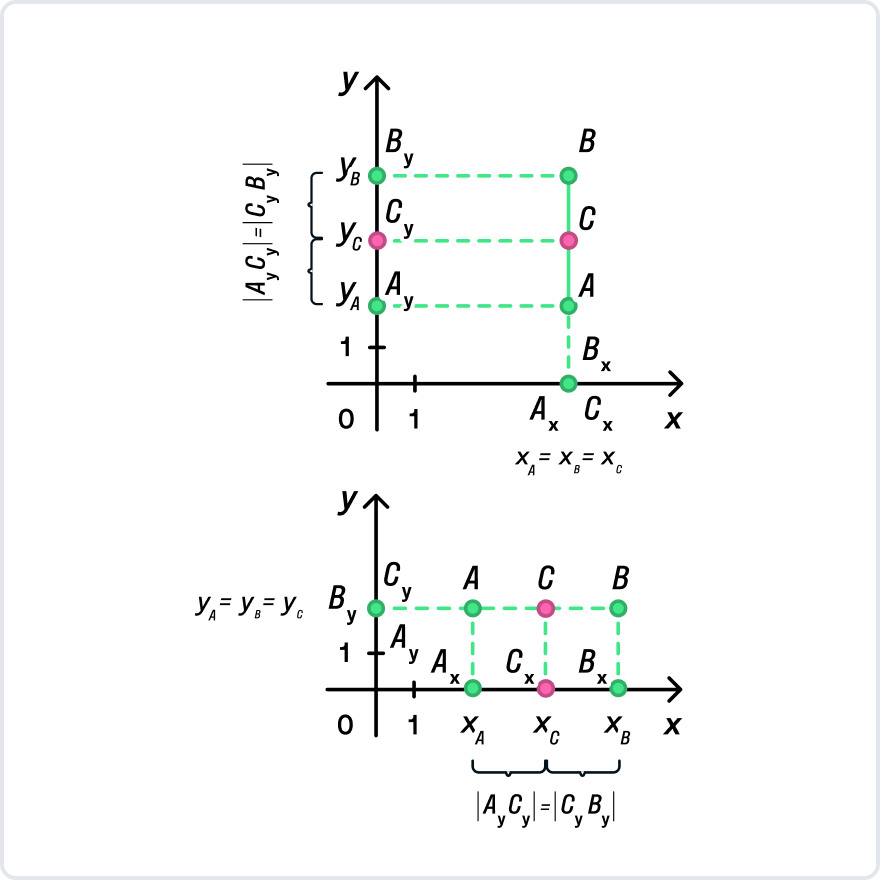
Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.
Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, ХА = ХС = ХВ. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: УА = УВ = УС.
И вновь пришло время задачек. Давайте разберем несколько примеров решения.
Задача 3
В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.
Решение
Обозначим середину отрезка точкой О. Тогда:
ХО = (ХС + ХК)/2 = (–6 + 2)/2 = –2,
УО = (УС + УК)/2 = (4 + 8)/2 = 6.
Ответ: О (-2; 6).
Задача 4
Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.
Решение
Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:
ХМ = (ХА + ХС)/2 = (–2 + 3)/2 = 0,5,
УМ = (УА + УС)/2 = (4 – 5)/2 = –0,5.
Ответ: М (0,5; –0,5).
Координаты середины отрезка в пространстве
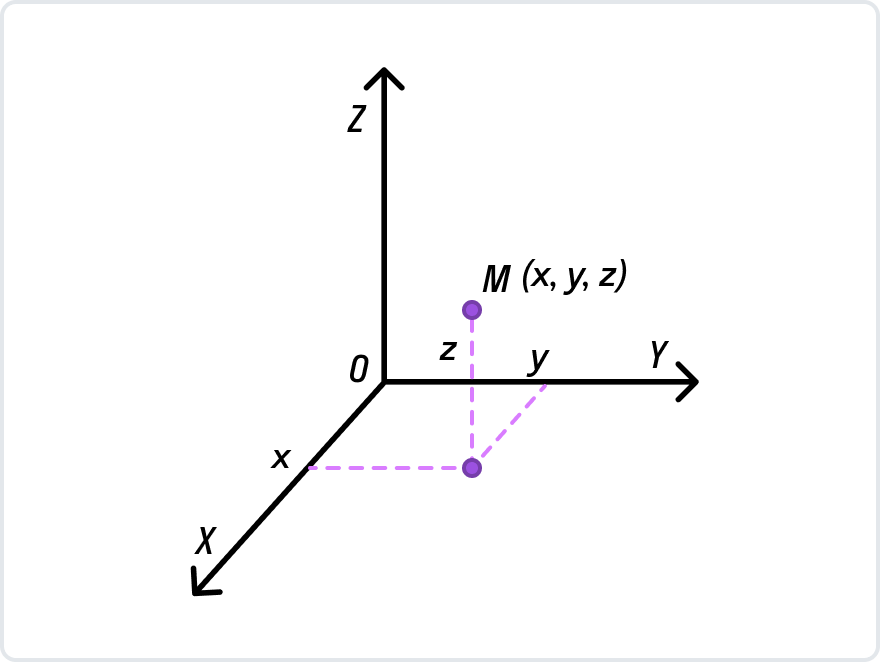
Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.
При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:
ХС = (ХА + ХВ)/2,
УС = (УА + УВ)/2,
ZС = (ZА + ZВ)/2.
Координаты середины отрезка через радиус-векторы его концов
По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру. Чтобы разобраться в нем, давайте сначала вспомним определение вектора.
Вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.
-
Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.
-
Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).
-
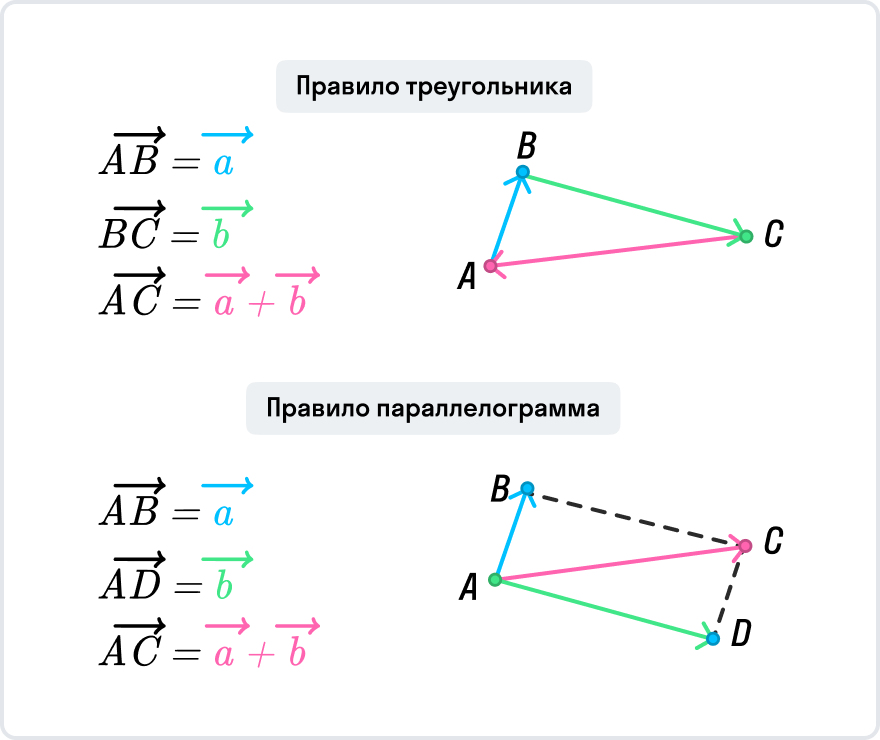
Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.
Радиус-вектор — вектор, который задает положение точки в пространстве относительно некоторой заранее фиксированной точки — начала координат.
Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор
с серединой в точке К. Координаты точки А (ХА; УА; ZА), К (ХК; УК; ZК), С (ХС; УС; ZС).Проведем радиус-векторы
,
,
.
Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).
ОА (ХА – 0, УА – 0, ZА – 0) = (ХА; УА; ZА),
ОК (ХК – 0, УК – 0, ZК – 0) = (ХК; УК; ZК,),
ОС (ХС– 0, УС – 0, ZС – 0) = (ХС; УС; ZС).
Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:
ХК = 1/2(ХА + ХО),
УК = 1/2(УА + УО),
ZК = 1/2(ZА + ZО).
Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.
Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.
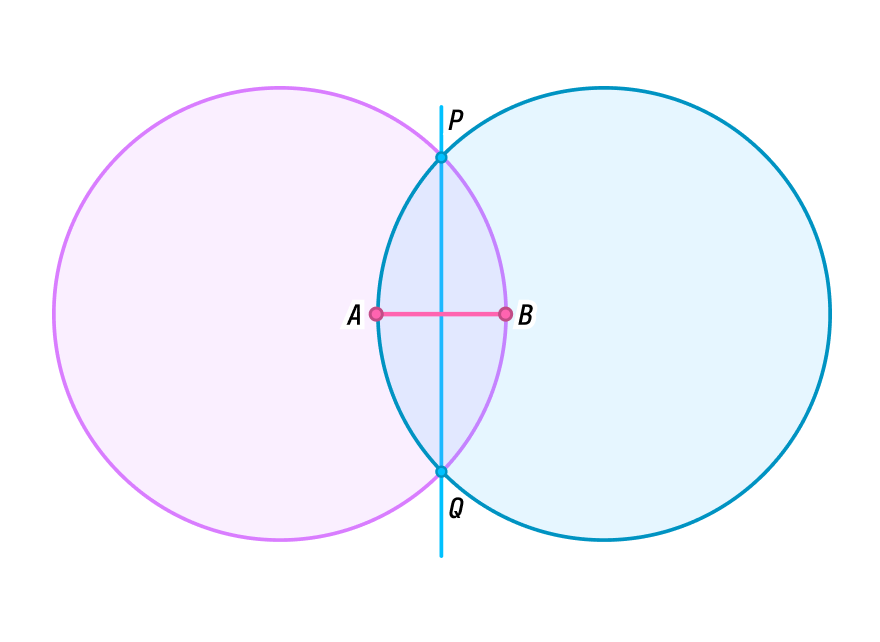
Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль. Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.
Мы видим, что окружности пересеклись дважды: снизу и сверху. Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.
Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!
Смешанные числа. Изображение обыкновенных дробей на координатном луче
Число, состоящее из целой части и дробной части, называется смешанным числом.
Чтобы неправильную дробь представить в виде смешанного числа, надо разделить числитель дроби на знаменатель, тогда неполное частное будет целой частью смешанного числа, остаток – числителем дробной части, а знаменатель останется тот же.
Чтобы представить смешанное число в виде неправильной дроби, нужно умножить целую часть смешанного числа на знаменатель, к полученному результату прибавить числитель дробной части и записать в числителе неправильной дроби, а знаменатель оставить тот же.
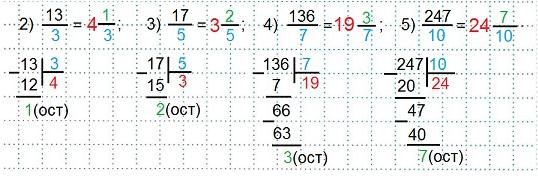
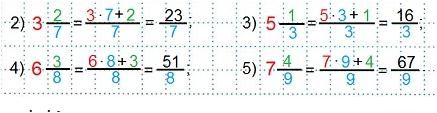
Примеры.
Дробная часть означает знак деления. В столбик разделим числитель13 на знаменатель 3. Частное 4 будет целой частью смешанного числа, остаток 1 станет числителем дробной части, а знаменатель 3 останется тот же.
Записать смешанное число в виде неправильной дроби:
Число 3 — целую часть смешанного числа умножают на знаменатель 7 дробной части, к полученному произведению прибавляют число 2— числитель дробной части смешанного числа; результат 23 станет числителем неправильной дроби, а знаменатель 7 останется тот же.
Изображение обыкновенных дробей на координатном луче
Для удобного изображения дроби на координатном луче важно правильно выбрать длину единичного отрезка.
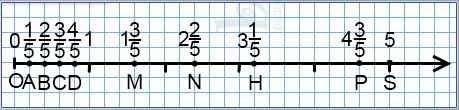
Самый удобный вариант отметить на координатном луче дроби — взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Например, если требуется изобразить на координатном луче дроби со знаменателем 5, единичный отрезок лучше взять длиной в 5 клеточек:
В этом случае изображение дробей на координатном луче не вызовет затруднений: 1/5 — одна клеточка, 2/5 — две, 3/5 — три, 4/5 — четыре.
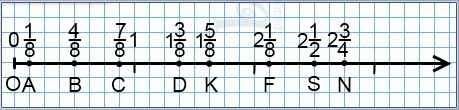
Если требуется отметить на координатном луче дроби с разными знаменателями, желательно, чтобы число клеточек в единичном отрезке делилось на все знаменатели. Например, для изображения на координатном луче дробей со знаменателями 8, 4 и 2 удобно взять единичный отрезок длиной в восемь клеточек. Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берем таких частей столько, каков числитель. Чтобы изобразить дробь 1/8, единичный отрезок разбиваем на 8 частей и берем 7 из них. Чтобы изобразить смешанное число 2 3/4, отсчитываем от начала отсчета два целых единичных отрезка, а третий разбиваем на 4 части и берем три из них:
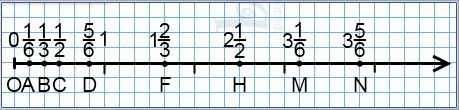
Еще один пример: координатный луч с дробями, знаменатели которых равны 6, 2 и 3. В этом случае в качестве единичного удобно взять отрезок длиной шесть клеточек:
Вопросы к конспектам
Даны точки и
. Найдите длину отрезка АВ.
На координатном луче даны точки В(а-3) и А(а+5) 7. Найдите длину отрезка АВ.
Запишите неправильную дробь в виде смешанного числа:
Запишите смешанное число в виде неправильной дроби:
Координаты точки середины отрезка в пространстве онлайн
Калькулятор рассчитывает координаты середины отрезка в пространстве по координатам конца отрезка с подробным порядком вычислений. В поля можно вводить целые или десятичные числа.
Введите координаты точки A
Введите координаты точки B
Определение середины отрезка
Середина отрезка — это точка которая лежит на отрезке, делит этот отрезок пополам и находится на равном расстоянии от начала и конца отрезка.
Формула расчёта координаты середины отрезка в пространстве
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
xc=(xa+xb)/2
yc=(ya+yb)/2
zc=(za+zb)/2
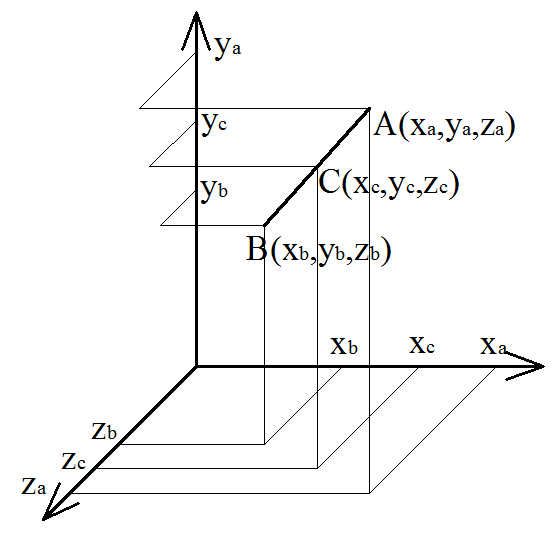
A(xa, ya, za), B(xb, yb, zb) — координаты концов отрезка
C(xc, yc, zc) — координаты середины отрезка
Разберём пример
Найдите координаты середины отрезка AC заданного точками A(4,5,7), C(10,11,5)
По формуле найдём координаты середины отрезка
x=(4+10)/2=7
y=(5+11)/2=8
z=(7+5)/2=6
Найдите координаты точки C середины отрезка AB заданного точками A(3,4,5), B(9,10,11)
xc=(3+9)/2=6
yc=(4+10)/2=7
yc=(5+11)/2=8
Найти координаты середины отрезка AB если A(4, 6, 1), B(5, 3, 2).
Найти координаты середины отрезка AB если A(4, 3, 1), B(5, 2, 0).
Найти координаты середины отрезка AB если A(0, 4, 4), B(2, 2, 3).
Найти координаты середины отрезка AB если A(0, 2, 4), B(2, 1, 3).
Похожие калькуляторы
Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Размерность:
Введите координаты точек.
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.