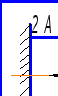
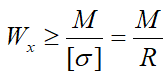Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:

где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов ().
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:

(3.10)
Для балки
прямоугольного сечения
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
.
Момент сопротивления
при изгибе
Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
Площадь
прямоугольного сечения
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
,
где М — максимальный
изгибающий момент, Нм;
W
— осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
где Wp
— полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим

Расчетная формула
для круглых валов принимает вид:

где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).
Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:

Примечание —
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
Плоскость хz:
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
Рисунок 3.12 —
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы
ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3
ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения
|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Покажем балку с построенными эпюрами Q и М
Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм.
Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров.

Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения:
Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:
Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Условие прочности по касательным напряжениям имеет вид:
Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h1=20 см, ширина полки b1=8 см.
Для поперечного сечения из двух швеллеров:
Sx= 2Sx1=2·95,9=191,8 см3,
Ix=2Ix1=2·1670=3340 см4,
b=2d1=2·0,52=1,04 см.
Определяем значение максимального касательного напряжения:
τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа.
Как видно, τmax <τadm (27МПа<75МПа).
Следовательно, условие прочности выполняется.
Проверяем прочность балки по энергетическому критерию.
Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН.
Проведем анализ напряженного состояния в точках сечения С
Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)
Уровень 1-1: y1-1=h1/2=20/2=10см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 2−2: y2-2=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 3−3: y3-3=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 4−4: y4-4=0.
Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 5−5:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 6−6:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 7−7:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых:
Используя энергетический критерий прочности, получим
Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется
(135,3 МПа<150 МПа).
Сечение балки подбирают по условию прочности при изгибе.
$$ sigma = frac{M_{ max } } { W } < [sigma] $$
где Mmax — максимальный момент в балке, определяется по эпюре (максимальный по модулю, то есть если есть моменты +36 и -47 кНм, то Mmax = 47 кНм);
$[sigma]$ — допускаемое напряжение, МПа (для стали Ст3 как правило 160МПа);
W — момент сопротивления сечения, см3.
Из этой формулы определяют необходимый момент сопротивления $W = frac{M_{ max } } { [sigma] }$, а по уго значению — размер сечения (по сортаменту для двутавра, швеллера и др. — или по формулам для прямоугольника, круга, ….).
Логичный вопрос — а зачем же тогда эпюра поперечных сил Q? Так вот, изгибающий момент приводит к нормальным напряжениям $sigma$, поперечная сила — к касательным $tau$. Но в большинстве балок нормальные напряжения в 10 — 100 раз больше касательных, и учитывать влияние касательных напряжений на прочность смысла никакого нет. Правда, в некоторых отдельных случаях касательные напряжения могут иметь весомы значения, например, изгиб коротких балок с тонкой стенкой (двутавр, труба и пр.)
Подбор размеров двутаврового и швеллерного профилей аналогичен, и представляет собой стандартную инженерную задачу.
Как известно из курса сопротивления материалов размеры элементов конструкций должны обеспечивать их прочность и жесткость.
Но одновременно с этим балки должны быть экономичными, то есть наименее металлозатратными и имеющими малый собственный вес.
Таким образом задача сводится к подбору таких размеров сечения, которые с одной стороны достаточны для того чтобы балка воспринимала рабочие нагрузки без нарушения несущей способности, а с другой – создают наименьший объем элемента.
Видео в котором показан типовой подбор двутавра:
Другие видео
Алгоритм подбора двутавра и швеллера
Подбор размеров симметричных форм прокатных профилей выполняется в следующей последовательности:
- Реальная конструкция заменяется расчетной схемой, выполненной в масштабе с указанием воздействующих на балку нагрузок. При этом элементы, не оказывающие влияния на схему нагружения, игнорируются.
- Для полученной расчетной схемы строятся эпюры распределения внутренних изгибающих моментов M.
- По эпюре M, определяется опасное сечение балки и величина максимального изгибающего момента Mmax.
- По формуле, которая следует из условия прочности при изгибе
где [σ] — допустимые напряжения,
R — расчетное сопротивление металла балки,
рассчитывается величина минимально необходимого расчетного момента сопротивления Wmin сечения, обеспечивающего прочность. - По сортаменту прокатной стали для соответствующего сечения балки выбирается номер профиля, значение Wx которого является ближайшим к расчетному в большую сторону.
Примечание. В случаях, когда балка состоит из двух и более одинаковых профилей общий момент сопротивления всего составного сечения увеличивается в соответствующее число раз, при условии что сечения расположены так, что их оси X совпадают.
Пример подбора двутаврового сечения балки >
Ответы на другие вопросы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее