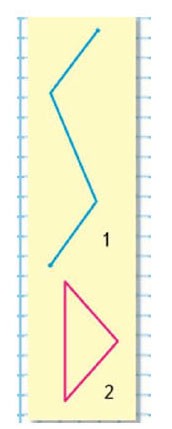
Как найти самопересечения ломаной - AvtoShod.ru

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019

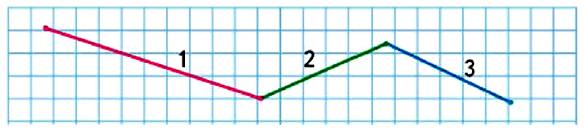
В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).

Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).

И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).

Нас будут интересовать замкнутые самопересекающиеся ломаные.

Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).

Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.

Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.

Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.

Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.

Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.

Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.

Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).

Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.

Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?

Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.

Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.

Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).

Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.

Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.

Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.

Художник Мария Усеинова

Источник

Ломаная линия

Замкнутая и незамкнутая ломаная
Самопересекающаяся ломаная
Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCDE.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Ответ: 17 см.

Источник

пишу программу, определяющую, является ли заданная в пространстве ломаная линия самопересекающейся. С клавиатуры задаются количество звеньев и координаты вершин по порядку.
Единственный алгоритм, который пока пришёл в голову — это попарная проверка на пересечение каждого с каждым отрезка через решение системы уравнений, состоящей из двух уравнений плоскости в пространстве.
Но подозреваю, что задачу можно решить легче, поскольку само по себе решение системы с шестью переменными — не такая простая задача, а для количества звеньев в несколько тысяч (надо сгенерировать именно такие тестовые наборы) работать решение будет занимать слишком долго и много по памяти.
Какой алгоритм можно использовать?

задан 19 окт 2020 в 10:34

что-то мне кажется задача легче O(n^2) не решается

например если ломанная представляет собой спираль, то никакими иными способами как проверка всех её звеньев задачу не решить

опять же может и есть какие-то оптимизации, то они лишь влияют на коэффициентик около n^2

так что да — алгоритм заключается в том чтобы

пройтись по всем звеньям кроме последнего —
```
 for (int i = 0; i < n - 1; i ++)
```
пройти по всем звеньям от текущего до последнего —
```
 for (int j = 0; j < n; j ++)
```
проверить отрезки [i], [j] на пересечение

https://e-maxx.ru/algo/segments_intersection_checking

в качестве оптимизации — не надо проверять отрезки, соединяющиеся с текущим, т.е.
```
 if ((i == j) || (abs(i - j) == 1))
     continue
```
в качестве оптимизации — не надо проверять отрезки до проверенного отрезка (поскольку их уже проверили), т.е.
```
 for (int j = i + 1; j < n; j ++)
```

условия 4) и 5) приводят к тому, что надо делать

    for (int i = 0; i < n - 1; i ++)
        for (int j = i + 2; i < n; j ++)

ответ дан 19 окт 2020 в 10:46

ZhiharZhihar

36.9k4 золотых знака25 серебряных знаков67 бронзовых знаков

Есть решение за O(n^2)(оно вами и описывалось). Смотрим на каждую пару отрезков, если хоть одна из этих пар пересекается, то ломаная самопересекающаяся, иначе — нет.

Особой проблемы в этом решении нет, если ограничения пару тысяч, то эта программа отработает меньше чем за секунду, а по памяти затраты будут ничтожны — нам необходимо хранить только координаты каждой точки.


for (int first = 0; first < n - 1; first++) {
    for (int second = 0; second < n - 1; second++) {
       if (first != second) //  говорим, что отрезки разные
          // в line содержится структурка, которая хранит координаты двух точек
          if (intersect (line[i], line[i+1], line[j], line[j+1]) {
                // нашли пересечение
          }
    }
}

Функцию пересечения отрезков можете подсмотреть здесь.

ответ дан 19 окт 2020 в 11:05

Источник

Содержание

Ломаная линия
Замкнутая и незамкнутая ломаная
Самопересекающаяся ломаная
Длина ломаной
Учебник Моро 2 класс. 1 часть. Страница 32
Учебник. Моро 2 класс 1 часть. Страница 32
Конспект по математике «Определение длины ломаной разными способами»
Дистанционное обучение как современный формат преподавания
Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО
Скоростное чтение
Оставьте свой комментарий
Безлимитный доступ к занятиям с онлайн-репетиторами
Подарочные сертификаты
Математика. 2 класс

Ломаная линия

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Длина ломаной

Пример 1. Найти длину ломаной из 3 звеньев.

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Источник

Учебник Моро 2 класс. 1 часть. Страница 32

Узнаем, как можно найти длину ломаной разными способами.
Будем учиться находить и сравнивать длины ломаных.

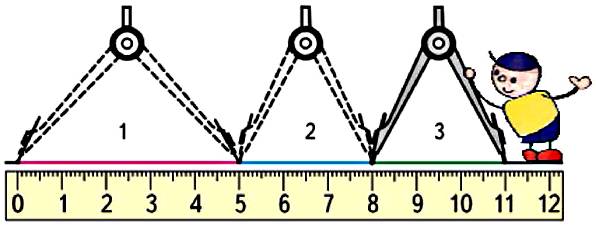
1. Длину ломаной можно узнать двумя способами.

1) Узнать длину каждого звена ломаной и найти сумму этих длин можно так: 5 + 3 + 3=11 (см).

2) Начертить прямую. С помощью циркуля отложить на прямой один за другим отрезки, равные по длине звеньям ломаной, и узнать длину всего получившегося отрезка (11 см).

В первом случае нужно сделать три измерения — измерить 3 звена ломаной.

Во втором случае я измерял только 1 раз — получившейся на прямой отрезок.

Вывод: Удобнее первый способ потому, что во втором случае надо чертить прямую и использовать циркуль. А в первом случае достаточно только измерить звенья линейкой и сложить получившиеся длины.

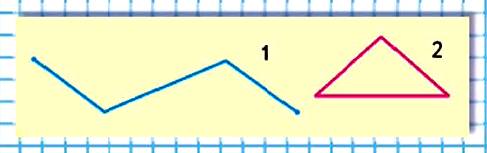
Задание 2

1) Узнай длину каждой ломаной.

Длина ломаной № 1 = 7 см
Длина ломаной № 2 = 7 см

2) Сравни ломаные и их длины.

Источник

Учебник. Моро 2 класс 1 часть. Страница 32

Длина ломаной

Узнаем, как можно найти длину ломаной разными способами.
Будем учиться находить и сравнивать длины ломаных.

1. Длину ломаной можно узнать двумя способами.

1) Узнать длину каждого звена ломаной и найти сумму этих длин можно так: 5 + 3 + 3=11 (см).

А можно так:

Сравни эти два способа: сколько измерений сделали в первом случае? во втором?

В первом случае я сделал три измерения — измерил 3 звена ломаной. Во втором случае я измерял только 1 раз — получившейся на прямой отрезок.

Сделай вывод.

Для меня удобнее первый способ потому, что во втором случае надо ещё чертить прямую и работать с циркулем. А в первом случае достаточно только измерить звенья линейкой и сложить получившиеся длины.

1) Узнай длину каждой ломаной.

Длина ломаной № 1 равна 7 см, а ломаной № 2 — 5 см.

2) Сравни ломаные и их длины.

Источник

Конспект по математике «Определение длины ломаной разными способами»

Конспект урока по математике.

учителя 2 класса Юдиной М.В.

04 декабря 2020 г.

Тема: Определение длины ломаной разными способами.

Тип: урок новых знаний.

Цель: учить находить длину ломаной разными способами.

Общеобразовательные: формировать умения находить длину ломаной разными способами применяя циркуль и линейку; закреплять знания о геометрических фигурах( точка, прямая, отрезок, ломаная); формировать умение работать с линейкой и карандашом, циркулем.

Коррекционно-развивающие: развивать внимание, логическое мышление, математическую речь; активизировать словарный запас; пополнить словарный запас.

Воспитательные: воспитывать интерес к предмету, аккуратность при черчении.

Который по счёту?

Мотивация. Сообщение темы урока.

Что на столе? (называние предметов для черчения: линейка, карандаш, циркуль)

Что будем делать?

Будем чертить _______ (слайд).

А) Активизация математического словаря.

Точка, прямая ,отрезок, ломаная.

Б) Понятие «ломаной».Части ломаной.

Будем учиться измерять длину ломаной.

В) Каллиграфическая минутка.

Г) Работа с книгой.

Открой книгу, страница 32. Прочитай тему урока.

Длина ломаной. Как можно узнать длину?

д) Работа с линейкой. Определение длины ломаной( 1 способ).

Возьми линейку, измерь первое звено, второе, третье.

Что нужно сделать, чтобы узнать длину? сложить.

Запиши в тетрадь.

е) Работа с циркулем. Определение длины ломаной (2 способ).

Возьми линейку и карандаш. Начерти длинную прямую.

Что это? (циркуль)

Возьми циркуль. Измерь первое звено. Перенеси длину звена на прямую, с помощью циркуля (второе, третье звено). Получился отрезок. Сколько сантиметров отрезок? Измерь линейкой.

а) Работа в парах.

Измерь длину разными способами.

б) Индивидуальные карточки.

Решение примеров с именованными числами.

1 дм 3 см + 2 дм 4см =

4 дм 3 см – 1 дм 1 см =

Определяли длину ломаной.

Было легко, трудно?

Самооценка деятельности на уроке.

Словесное оценивание учителем.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Сейчас обучается 322 человека из 58 регионов

Курс повышения квалификации

Скоростное чтение

Сейчас обучается 622 человека из 79 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1555922

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

В Тюменской области продлили на неделю дистанционный режим для школьников

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс. Урок №13.

Длина ломаной. Закрепление

Перечень вопросов, рассматриваемых в теме:

— Как найти длину ломаной?

Глоссарий по теме:

Ломаная — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.

Звенья — отрезки, из которых состоит ломаная.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина ломаной – это сумма длин всех её звеньев.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35

2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 — с.20, 21

3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 — с.20, 21, 25

Теоретический материал для самостоятельного изучения

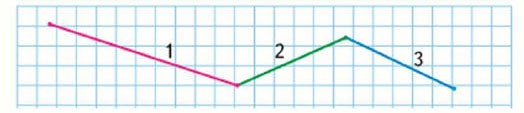
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.

Как найти длину ломаной линии? Это можно сделать двумя способами.

Первый способ. Сначала узнаем длину каждого звена с помощью линейки

Длина первого звена 4 см.

Длина второго звена 6 см.

Длина третьего звена 5 см.

Найдем сумму этих длин.

Найдем длину ломаной вторым способом.

Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.

Накладываем циркуль на второй отрезок, переносим его на прямую.

Накладываем циркуль на третий отрезок, переносим его на прямую.

Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.

Выводы: длину ломаной можно находить двумя способами.

Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.

Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.

1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см

10 см 8 см 7 см

2. Расположите ломаные линии по порядку: от самой короткой до самой длинной

Правильный вариант: Найдем длину каждой ломаной

Источник

Ломаная линия

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

lom ln

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

lom ln2

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

lom ln3

замкнутая ломаная ABC.

Самопересекающаяся ломаная

lom ln4

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

lom ln5

Длина ломаной

Пример 1. Найти длину ломаной из 3 звеньев.

lom ln6

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

lom ln7

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Источник

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 18

Источник

Ищем педагогов в команду «Инфоурок»

Выбранный для просмотра документ Косычев Н. Линии.doc

Муниципальное бюджетное общеобразовательное учреждение «Гимназия»

Удивительный мир линий

выполнил: ученик5б класса

Косычев Николай Владимирович

руководитель: учитель математики

2.1 Определение линий………………

2.2 Классификация линий……………………………………

3.1 Решение разных задач с линиями

3.2 Линии в окружающем нас мире

IV . Источники информации

Мир линий разнообразен и красив.

Тема проекта: Удивительный мир линий

Цель: изучить и найти различные области применения линий

Дать определение линии

Рассмотреть классификацию линии

Увидеть линии в окружающем нас мире

2.1. Что такое линия

Карандаш на бумаге оставляет след…

Мел на асфальте тоже оставит свой след…

Таких примеров много- и все это ЛИНИИ

Линия – это геометрическая фигура, которая может быть получена в результате непрерывного перемещения точки.

2.2 Классификация линий

Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:

Линии разжеляются на прямые и кривые линии.

Источник

Точка и линия

Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.

Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.

Зачем нужна точка, если она воображаемая? Для чего ее придумали?

Точка выполняет только одну задачу: указание месторасположения.

Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.

Линия – это множество точек, расположенных последовательно друг за другом.

Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.

Рис. 1 Цепь и линия

Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.

Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?

Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.

Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.

Рис. 2 Путь автомобиля

Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.

Рис. 3 Контур и диапазон

Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.

Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.

Обозначение точек и линий

Рис. 4 Обозначение точек и линий

Взаимное расположение точек и линии

Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.

Рис. 4.1 Принадлежность точек линии

При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H

Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:

Виды линий

Рис. 5 Замкнутая и незамкнутая линия

Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.

Рис. 6 Контур птицы

Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).

Рис. 7 Незамкнутые линии

Еще несколько примеров.

1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.

08 way

2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.

3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.

Также линии бывают:

Рис. 11 Самопересекающиеся и не самопересекающиеся линии

Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.

Рис. 12 Прямая, ломаная, кривая линии

Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.

Источник

Замкнутые самопересекающиеся ломаные

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019

Нас будут интересовать замкнутые самопересекающиеся ломаные.

Задача 1

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно два раза?

Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.

Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.

Задача 2

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно один раз?

Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.

Упражнения и задачи для самостоятельного решения

1. Может ли прямая, не содержащая вершин замкнутой девятизвенной ломаной, пересечь каждое её звено?

2. (В. Произволов) Замкнутая ломаная такова, что каждые два её не соседних звена пересекаются. Докажите, что у этой ломаной нечётное количество звеньев.

3. Существует ли пятнадцатизвенная ломаная, пересекающая каждое своё звено ровно три раза?

4. Постройте восьмизвенную замкнутую ломаную, которая каждое своё звено пересекает один раз.

5. (Д. Калинин, вариация фольклора) Маша нарисовала замкнутую семизвенную ломаную. Для каждого звена она записала, со сколькими звеньями оно пересекается во внутренних точках. Могла ли она записать в каком-то порядке числа 1, 2, 3, 4, 3, 2, 1?

6. Какое наибольшее количество точек самопересечения может иметь замкнутая семизвенная ломаная?

7. (Н. Васильев) Рассматриваются всевозможные шестизвенные замкнутые ломаные, все вершины которых лежат на окружности.

Источник

Александр Блинков, Александр Грибалко «Квантик» №11, 2019

Ломаная линия

Замкнутая и незамкнутая ломаная

Самопересекающаяся ломаная

Длина ломаной

Ломаная линия

Замкнутая и незамкнутая ломаная

Самопересекающаяся ломаная

Длина ломаной

Учебник Моро 2 класс. 1 часть. Страница 32

Учебник. Моро 2 класс 1 часть. Страница 32

Конспект по математике «Определение длины ломаной разными способами»

Дистанционное обучение как современный формат преподавания

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Скоростное чтение

Оставьте свой комментарий

Безлимитный доступ к занятиям с онлайн-репетиторами

Подарочные сертификаты

Математика. 2 класс

Конспект урока

Ломаная линия

Замкнутая и незамкнутая ломаная

Самопересекающаяся ломаная

Длина ломаной

Плоскость, прямая линия, луч

Прямая линия

Обозначение прямой

Некоторые свойства прямой

Обозначение луча

Точка и линия

Обозначение точек и линий

Взаимное расположение точек и линии

Виды линий

Замкнутые самопересекающиеся ломаные

Задача 1

Задача 2

Упражнения и задачи для самостоятельного решения

Не пропустите также:

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019