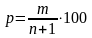(кг/м3) – плотность
(н/м3) – удельный вес
ГИДРОСТАТИКА
р — давление или сжимающие напряжение (н/м2 = Па)
Свойства:
Давление всегда направлено к поверхности по внутренней нормали.
Действует одинаково по всем направлениям (не зависит от угла наклона площадки)
Основное уравнение гидростатики:
рА = ро + рв; рв = h·γ
рА – абсолютное давление;
ро – давление действующее на поверхность жидкости;
рв – весовое давление, т.е. давление столба жидкости.
рв = h·γ
h – глубина расположения точки;
γ – удельный вес жидкости.
При атмосферном давлении на поверхности:
рА = ра + ризб; ризб = hизб·γ
ра – атмосферное давление;
ризб – избыточное давление.
Выводы:
-
Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.
-
Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.
-
Можем измерять величину давления эквивалентной ему высотой столба жидкости.
р = h·γ, отсюда h = р/γ
Например давление величиной в 1 атм. р = 1 кгс/см2 соответствует
h = 10 м вод. столба
Сила давления жидкости на плоскую поверхность
Р = рсS = hсγS (н)
рс = hсγ – давление в центре тяжести при атмосферном давлении на поверхности
рс = hсγ + рМ, либо рс = hсγ – рВАК
hс – глубина расположения центра тяжести поверхности (м);
S – площадь поверхности (м2).
Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости
Удельная энергия (напор) Э = Е/G = Е/mg (м)
Z + hп = НГС = Э = const
Z – геометрический напор;
hп – пьезометрический напор;
НГС –гидростатический напор или полная удельная потенциальная энергия жидкости.
ГИДРОДИНАМИКА
Уравнение неразрывности
Q = V1ω1 = V2ω2 = const
Q – расход жидкости (м3/с);
V – средняя скорость потока (м/с);
Ω – площадь живого сечения потока (м2).
Vi = Q / ωi – средняя скорость потока
Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)
где z — геометрический напор, м;
P/γ — приведенная пьезометрическая высота (если Р — абсолютное давление) или пьезометрическая высота (если Р — избыточное давление), м;
V2/2g — скоростной напор, м.
— гидростатический напор,
удельная потенциальная энергия жидкости
НГС = Э – гидродинамический напор или полная удельная энергия
Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).
Σh = hпот = hℓ + hм – потери энергии при движении жидкости от 1 до 2 сечений (м);
α= ЕКД /ЕКУ – коэффициент кинетический энергии (коэффициент Кориолиса);
hℓ — потери по длине.
(м)
λ – коэффициент гидравлического трения f(Rе·Δ);
hм – потери на местных сопротивлениях.
(м)
РЕЖИМЫ ДВИЖЕНИЯ
Число (критерий) Рейнольдса
Для кругло-цилиндрических труб
(м)
RГ – гидравлический радиус;
ω – площадь живого сечения потока (м2);
Х – смоченный периметр.
Ламинарный режим: Rе < Rекр ≈ 2320
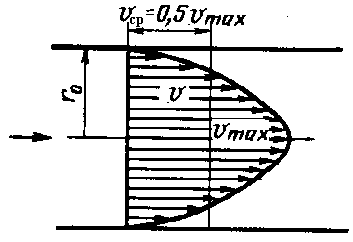
Эпюра скорости при ламинарном движении.
umax = 2V; α = 2; λ = f(Rе); λ = 64/Rе; hℓ = f (V1…1,4)
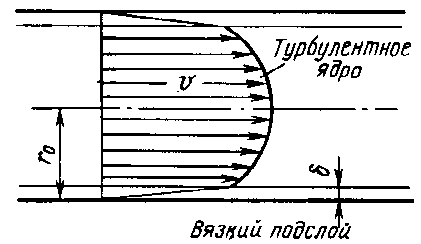
Турбулентный режим: Rе > Rекр
Профиль скорости при турбулентном движении
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)
u ≈ V; α = 1…1,4
В турбулентном режиме имеется три вида трения:
Гидравлически гладкие русла
λ = f(Rе) λ = 0,3164/Rе0,25
Смешанное трение
λ = f(Rе;Δ)
Шероховатое трение, квадратичная область турбулентного режима
λ = f (Δ); λ = 0,11(Δ /d)0,25
hℓ = f (V1,7…2)
СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
(м/с)
— коэффициент скорости
Но – действующий (расчетный напор (м)
Расход жидкости
(м3/с)
μ = φε – коэффициент расхода;
ω – площадь проходного (живого) сечения потока (м2);
Но – действующий напор (м).
Слой стока — это гидрологический показатель, который показывает каким слоем воды в миллиметрах можно полностью залить водосбор, если бы вода распределялась по его территории равномерно.
Рассчитывается очень просто:
Объем стока делится на площадь бассейна реки.
h = W / (F х 1000)
1000 — это для того, чтобы перевести квадратные километры в квадратные метры.
Между прочим, при гидрологических расчетах используются не данные по годовому стоку реки, а данные по ежедневным расходам воды, которые выбираются из гидрологических справочников.
Действие первое — находим средний расход воды, для чего сумму всех расходов делим на 365 или 366 (последнее если год високосный)
Действие второе — находим объем стока, для чего средний расход воды умножаем на количество секунд в году
Действие третье — находим слой стока по формуле, указанной выше.
Кстати, для тех, кто в «танке» — слой стока на территории Беларуси составляет примерно 200-300 миллиметров. Получили цифру, которая намного больше или намного меньше — лучше пересчитайте, так как в расчетах явная ошибка.
-
Основные расчетные гидрологические характеристики (ргх). Методы определения ргх при достаточной продолжительности наблюдений.
К
основным гидрологическим характеристикам
относятся:
-расход
воды Q, м³/с;
-объем
стока воды W, м³;
-модуль
стока воды q, м³/с·км²;
-слой
стока воды h, мм;
-уровень
воды Н, см.
Способы
определения расчетных гидрологических
характеристик зависят от наличия и
продолжительности гидрометрических
наблюдений.
Поведение
случайных величин, которые составляют
заданный гидрологический ряд наблюдений,
можно охарактеризовать тремя параметрами:
—
средним арифметическим значением;
—
коэффициентом вариации;
—
коэффициентом асимметрии.
Среднее
арифметическое значение ряда:

где:
Qi – максимальный расход весеннего
половодья, м³/с;
n
– количество членов ряда.
Коэффициенты
вариации и асимметрии определяются в
соответствии с СП 33-101-2003 методами
моментов и наибольшего правдоподобия.
1.
Метод моментов.
Коэффициент вариации Сv характеризует
меру изменчивости членов ряда относительно
среднего арифметического значения и
определяется по формуле (при Сv < 0.6):
,
где
Ki – частное от деления i-го члена ряда
на среднее арифметическое этого ряда,
т.е.
.
Коэффициент
асимметрии Сs характеризует отличие по
величине и количеству положительных
(больше средних) и отрицательных (меньше
средних) отклонений от среднего
арифметического значения ряда. Для
симметричных рядов (нормальное
распределение ежегодных вероятностей
превышения значений ряда) эти отклонения
повторяются одинаково часто, поэтому
Cs = 0. Для несимметричных рядов Cs ≠ 0,
а коэффициент асимметрии определяется
по формуле (при Сs < 1,0):

В
верхней строке этой таблицы указана
точность, с которой необходимо определить
соответствующие величины.
Для
проверки правильности определения
среднего значения сравниваем суммы
положительных и отрицательных значений
∑(Ki — 1). Они должны отличаться один от
другого не более чем на 5%.
2.
Метод наибольшего
правдоподобия.
Для оценки коэффициентов вариации и
асимметрии этим методом необходимо
предварительно определить величины
статистик:


Результаты
расчета, необходимые для определения
этих статистик, сводятся в табл. 1. По
рассчитанным значениям статистик по
одной из номограмм определяют
характеристики ряда: Cv, Cs/Cv и Cs.
3
.
После определения параметров
статистического ряда этими методами,
находятся ординаты (модульные
коэффициенты) теоретической (аналитической)
кривой трехпараметрического
гамма-распределения ежегодных вероятностей
превышения значений гидрологической
характеристики или кривой обеспеченности.
По ним вычисляем максимальные расходы
воды заданной обеспеченности Qр% =
Кр% * Qср.
1
– эмпирическая
2
– метод моментов
3
– метод наибольшего правдоподобия
-
Основные расчетные гидрологические характеристики (ргх). Удлинение недостаточного ряда гидрологических наблюдений.
К
основным гидрологическим характеристикам
относятся:
-расход
воды Q, м³/с;
-объем
стока воды W, м³;
-модуль
стока воды q, м³/с·км²;
-слой
стока воды h, мм;
-уровень
воды Н, см.
При
недостаточности данных гидрометрических
наблюдений на реке В параметры кривой
обеспеченности гидрологических
характеристик стока или уровней воды
необходимо привести к многолетнему
периоду используя данные реки-аналога
(рек-аналогов) и методы парной или
множественной регрессии. При
этом необходимо выполнить следующие
условия:
—
река-аналог или реки-аналоги должны
отвечать указанным ниже требованиям;
—
число совместных наблюдений на
рассматриваемой реке и реках-аналогах
должно быть не менее 6 лет при одном
аналоге, и не менее 10 лет при двух и более
аналогах;
—
коэффициент корреляции между стоком в
приводимом пункте и пунктах рек-аналогов
должен быть не менее 0,7;
—
коэффициент достоверности (не случайности)
корреляции должен быть не менее 2;
Основными
требованиями, предъявляемыми к
реке-аналогу, являются:
—
географическая близость расположения
водосборов;
—
однородность условий формирования
стока реки-аналога и исследуемой реки:
сходство климатических условий,
однотипность почв и грунтов,
гидрогеологических условий, близкие
степени озерности, залесенности,
заболоченности и распаханности);
—
отсутствие факторов, существенно
искажающих естественный речной сток
(регулирование стока, сбросы и изъятия
воды и др.).
Мерой
тесноты связи между двумя статистическими
рядами служит коэффициент корреляции,
определяемый по формуле:
,
где
Δ Xi = Хi – Xc; Δ Yi = Yi – Yc;
Xi
и Yi – соответствующие друг другу (по
годам) ежегодные расходы воды с количеством
членов n лет;
Хс
, Yc – средние арифметические значения
рядов, т.е. Хс = ∑ Хi / n; Yc =
∑ Yi / n.
Уравнение
регрессии, которое предполагается
использовать для удлинения ряда по
данным одной реки-аналога, имеет вид:

где
σу, σх – средние квадратические
отклонения, определяемые по формулам:

Для
оценки возможности применения уравнения
регрессии для удлинения гидрологического
рядя предварительно необходимо
определить:
—
среднее квадратическое отклонение
коэффициента корреляции:
—
критерий достоверности (не случайности)
коэффициента корреляции:
При
r ≥ 0.7 и Кд ≥ 2 корреляционная связь
между гидрологическими рядами считается
достоверной, а уравнение регрессии
может быть использовано для удлинения
гидрологического ряда для реки В.
При
использовании нескольких рек-аналогов
(j) удлинение гидрологического ряда
производится по уравнению множественной
линейной регрессии:
Yi
= K0 + K1 * (X1)i + K2 * (X2)i + … + Kj * (Xj)i,
где
K1…Kj – значения стока или уровней воды
в реках-аналогах (1…j);
K0
– свободный член;
K1…Kj
– коэффициенты уравнения регрессии.
Коэффициенты
и свободный член этого уравнения
определяют методом наименьших квадратов
(МНК).
При
использовании графического метода
удлинения ряда наблюдений строится
график связи между соответствующими
расходами воды. Недостающие значения
расхода воды для рассматриваемой реки
определяются приближенно по этому
графику. При этом целесообразно построить
такие графики для нескольких рек-аналогов,
из которых для удлинения ряда принимают
график, имеющий наибольший коэффициент
корреляции. Этот метод допускается
применять на начальных этапах
проектирования гидротехнических
сооружений.
14.
Эмпирическая
обеспеченность. Кривая обеспеченности.
Эмпирическую
обеспеченность или ежегодную вероятность
превышения гидрологических характеристик
определяют по формуле:
,
%
где
m – порядковый номер члена ряда,
выстроенного в убывающем порядке.
1
– эмпирическая
2
– метод моментов
3
– метод наибольшего правдоподобия
15.
Требования
к выбору места мостового перехода.

16.
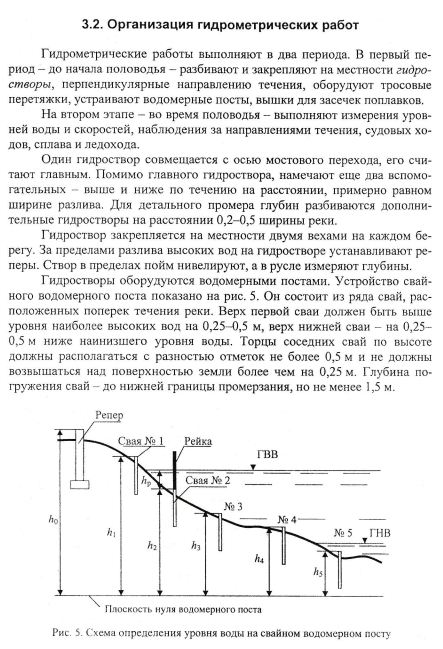
Организация
гидрометрических работ (разбивка
гидростворов, оборудование водомерного
поста).
17.
Измерение
уровней и уклонов поверхности воды в
реке.
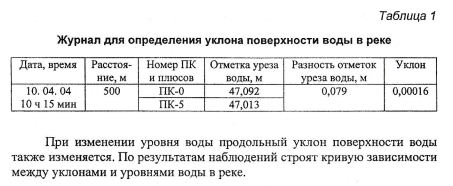
18.
Измерение
глубин воды в реке.
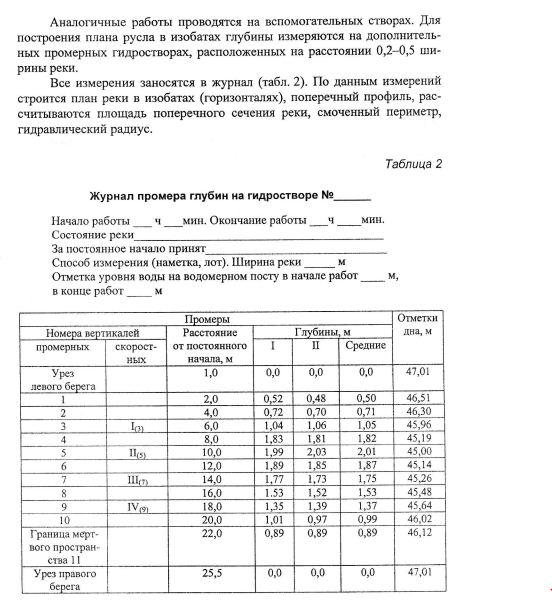
19.
Измерение глубин воды в реке.

20.
Определение
расхода воды в реке по данным вертушечных
измерений.
21.
Формула
Шези.
22.
Устройство
гидрометрической вертушки.

Соседние файлы в предмете Гидрология
- #
- #
- #
- #
- #
- #