Equivalent resistance is defined as the total resistance of the circuit for the resistors connected in series or parallel combination. Resistors are electrical devices that limit the current flow in a circuit and obey Ohm’s law, V = IR. A circuit may have more than one resistor present due to which equivalent resistance is evaluated accordingly. The value of current and voltage depends on the orientation of resistors in the circuit.
In this article, we will learn about the Equivalent Resistance Formula in Series and Parallel combinations in detail.
What is the Equivalent Resistance?
Equivalent Resistance is the total resistance of the combination of all the resistances in the circuit. Suppose there are n resistance added in the circuit either in series or in parallel combination and if we replace all the resistance with a single resistance such that the current and the voltage difference in the circuit do not change it is called equivalent resistance.
Unit of Equivalent Resistance
Equivalent resistance is denoted by the symbol Req. SI unit of the measurement of Equivalent Resistance is Ohm (Ω) and the dimensional formula of the Equivalent Resistance [M1L2A−2T−3].
Formula for Equivalent Resistance
Equivalent Resistance is calculated using the Equivalent Resistance Formula, and the equivalent resistance formula is different in series and parallel combinations, i.e., we have two different equivalent resistance formulas they are,
- Equivalent Resistance Formula for Series Combination.
- Equivalent Resistance Formula for Parallel Combination.
Now, let’s learn about both formulas in detail in this article,
Equivalent Resistance Formula for Series Combination
In a series circuit of resistors, n resistors (n > 1) are connected adjacently one after the other, such that the collection of these resistors can be replaced by a single equivalent resistor to give the same resistance value. Here, the sum of the individual resistances will be the equivalent resistance of a series of resistors. The current through each resistor is the same but the voltage gets divided into n parts among the resistors.
Req = R1 + R2 + R3 + ….. + Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
Equivalent Resistance Formula for Parallel Combination
In a parallel circuit of resistors, n resistors (n > 1) are connected parallelly via wires that start from a common point. Here, the sum of the reciprocals of individual resistances equals the reciprocal of the equivalent resistance. The voltage through each resistor is the same but the current gets divided into n parts among the resistors.
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
How to find Equivalent Resistance?
The equivalent resistance of any circuit can easily be calculated using the steps given below,
Step 1: Study the electric circuit and mark all the resistance in the circuit along with the voltage of the battery.
Step 2: Check whether the resistance added is in series or parallel combination or both.
Step 3: Use the Equivalent Resistance Formula for Series Combination or Parallel combination accordingly.
Step 4: Simplify the formula in step 3 to get the Equivalent Resistance.
Read, More
- Electrical Resistance and Resistivity
- Temperature Dependence of Resistance
- Electrical Resistance Formula
Solved Examples on Equivalent Resistance Formula
Example 1: What is the equivalent resistance if three resistances of 4 Ω, 2 Ω, and 5 Ω are connected in series?
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 5 ΩUsing the formula we get,
Req = R1 + R2 + R3
= 4 + 2 + 5
= 11 Ω
Example 2: Find the unknown resistance if three resistances of 2 Ω, 5 Ω, and x Ω are connected in series to give an equivalent resistance of 10 Ω.
Solution:
We have,
R1 = 2 Ω
R2 = 5 ΩReq = 10 Ω
Using the formula we get,
Req = R1 + R2 + R3
10 = 2 + 5 + x
10 = 7 + x
x = 3 Ω
Example 3: Find the unknown resistance if three resistances of 7 Ω, 3 Ω, and X Ω are connected in series to give an equivalent resistance of 15 Ω.
Solution:
We have,
R1 = 7 Ω
R2 = 3 ΩReq = 15 Ω
Using the formula we get,
Req = R1 + R2 + R3
15 = 7 + 3 + X
15 = 10 +
x = 5 Ω
Example 4: What is the equivalent resistance if three resistances of 6 Ω, 3 Ω, and 8 Ω are connected in parallel?
Solution:
We have,
R1 = 6 Ω
R2 = 3 Ω
R3 = 8 ΩUsing the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3
1/Req = 1/6 + 1/3 + 1/8
1/Req = (4+8+3)/24
1/Req = 15/24
Req = 24/15 Ω = 1.6 Ω
Example 5: Find the unknown resistance if three known resistances of 4 Ω, 2 Ω, and 1 Ω connected in series with an unknown resistance of X Ω give an equivalent resistance of 0.5 Ω.
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 1 ΩReq = 0.5 Ω
Using the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3 + 1/R4
1/0.5 = 1/4 + 1/2 + 1/1 + 1/R4
1/R4 = 1/4 + 1/2 + 1/1 – 1/0.5
1/R4 = 1/4
R4 = 4 Ω
FAQs on Equivalent Resistance Formula
Question 1: What is the “equivalent resistance” formula in the Series combination?
Answer:
The “equivalent resistance” formula in the Series combination is given below,
Req = R1 + R2 + R3 + ….. + Rn
Question 2: What is the condition for the series combination of resistance?
Answer:
For the resistor to be connected in series combination the important conditions are,
- The current passing through each resistor is the must be same.
- The resistors are connected in a linear manner.
Question 3: What is the “equivalent resistance” formula in the Parallel combination?
Answer:
The “equivalent resistance” formula in the Parallel combination is given below,
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
Question 4: What is the condition for the parallel combination of resistance?
Answer:
For the resistor to be connected in parallel combination the important conditions are,
- The voltage difference across each resistor is the same.
- The resistors are connected parallel to each other.
Last Updated :
21 Mar, 2023
Like Article
Save Article
Введение
Решение задач — неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:
- Выдвижение проблемы и создание проблемной
ситуации; - Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.
§1. Задачи по расчету электрических
цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:
1) содержат большое число элементов –
резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений
элементов.
В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.
Рассмотрим примеры решения задач эти методом.
З а д а ч а №1
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная
схема:
Ее сопротивление и сопротивление исходной цепи
RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB
равно:
RAB= (8/10)*r.
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных
угла О1 и О2. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
З а д а ч а №9
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С1 и С2.
Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их
в один узел ОI .Эквивалентная схема
изображена на рисунке :
Сопротивление на участке А ОI равно . На участке
ОIВ сопротивление равно .Получаем совсем
простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему
сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.
Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.
Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов; - начертить эквивалентную схему;
- найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом участке по законам
последовательного и параллельного соединения; - начертить эквивалентную схему, заменяя участки
соответствующими им расчетными сопротивлениями; - пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи. - Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.
Примеры:
1)
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.
2)
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения
сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.
в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.
Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.
Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.
Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную
схему:
Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. —
М: Просвещение,1983. - Лукашик В.И. Физическая олимпиада.- М:
Просвещение, 2007 - Усова А.В., Бобров А.А. Формирование учебных
умений и навыков учащихся на уроках физики.- М:
Просвещение,1988 - Хацет А. Методы расчета эквивалентных схем
//Квант. - Чертов А. Г. Задачник по физике. – М.: Высшая
школа,1983 - Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г. Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические
материалы. Москва, “Дрофа”, 2004г
Как найти эквивалентное сопротивление цепи формула
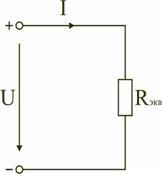
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
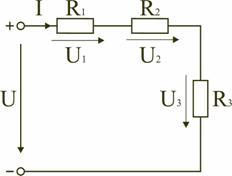
Электрическая цепь с последовательным соединением элементов
Рис. 1.4
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
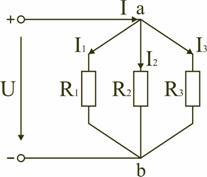
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.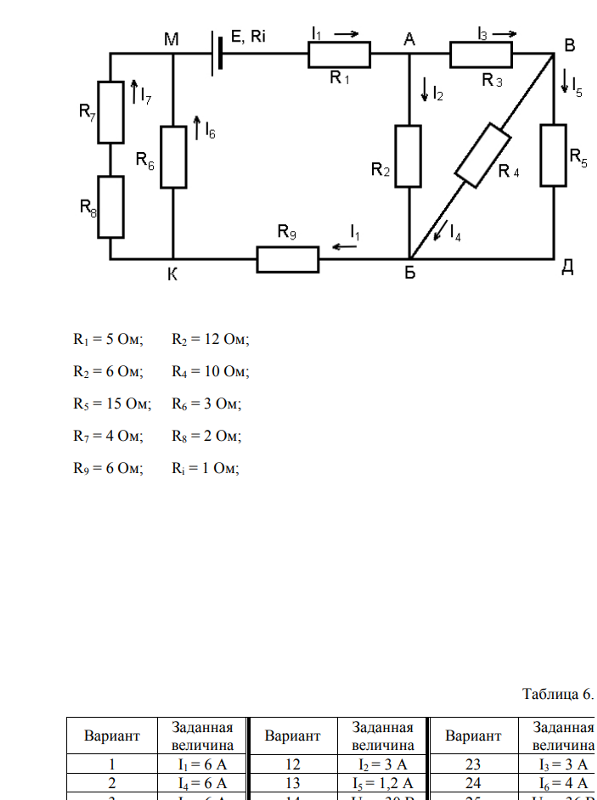
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
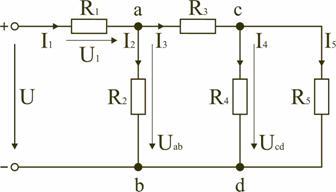
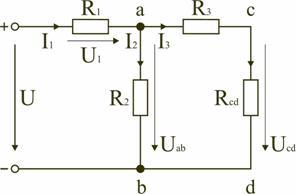
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
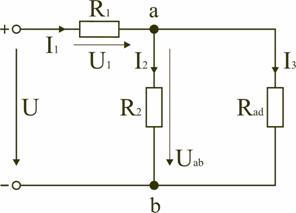
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
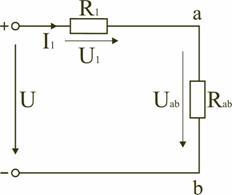
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
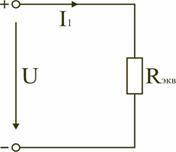
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
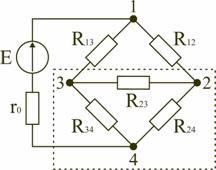
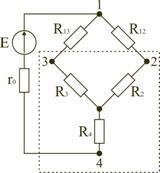
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 1.12
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник».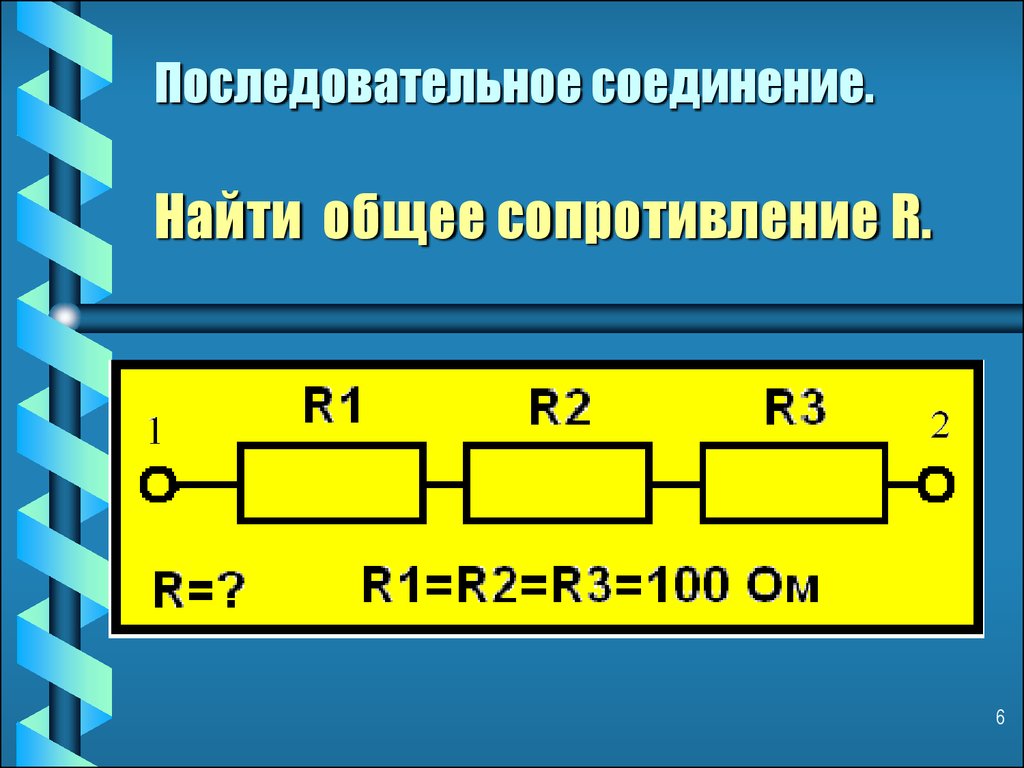
; ; .
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
; ; .
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис.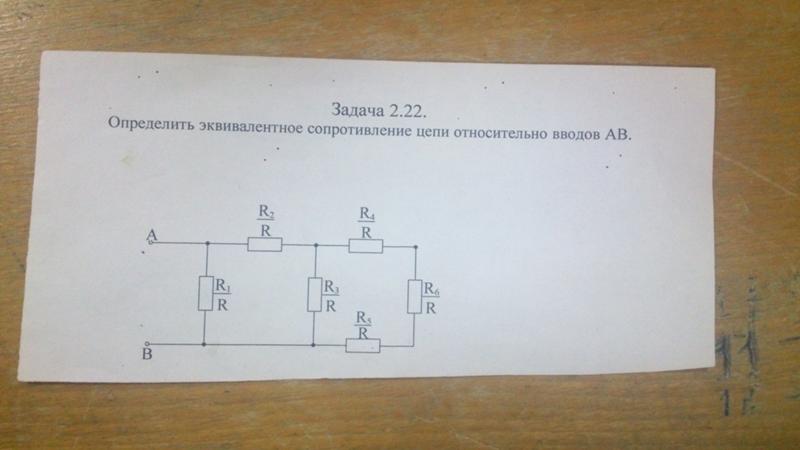
Электрическая цепь с последовательным соединением элементов
Рис. 1.4
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис.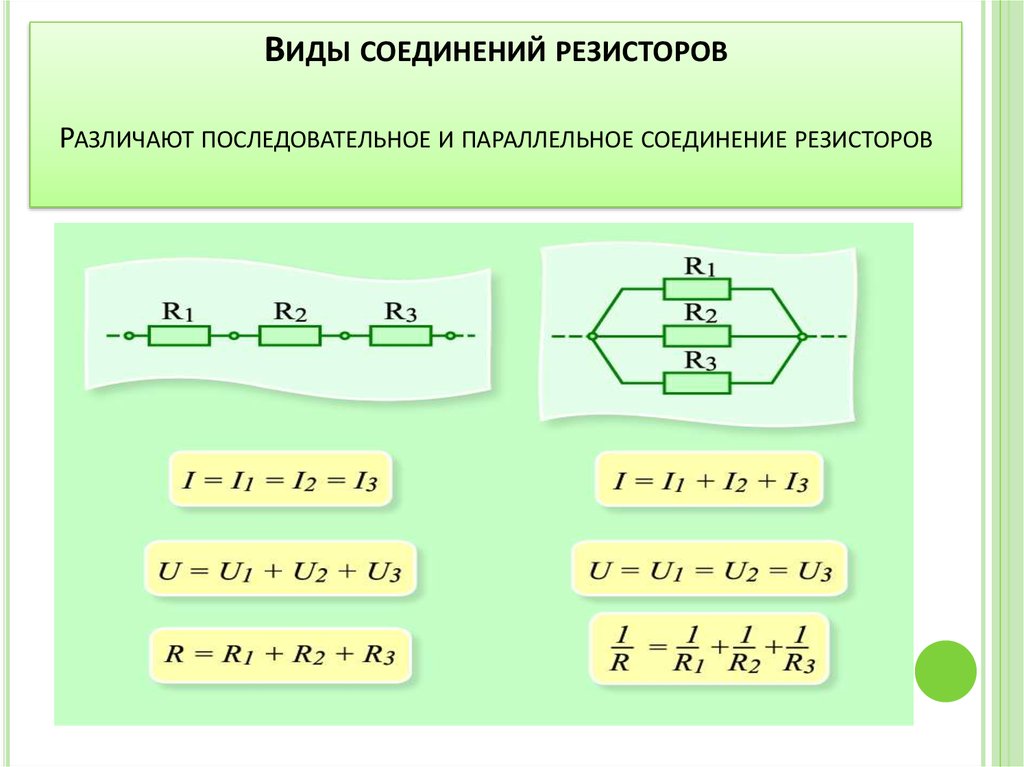
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е. ,
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв.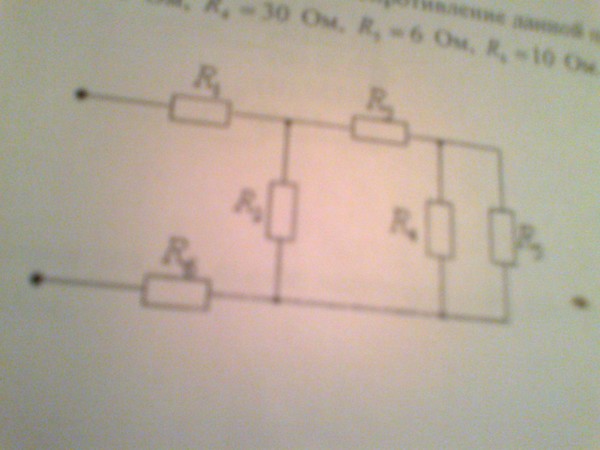
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 1.12
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи.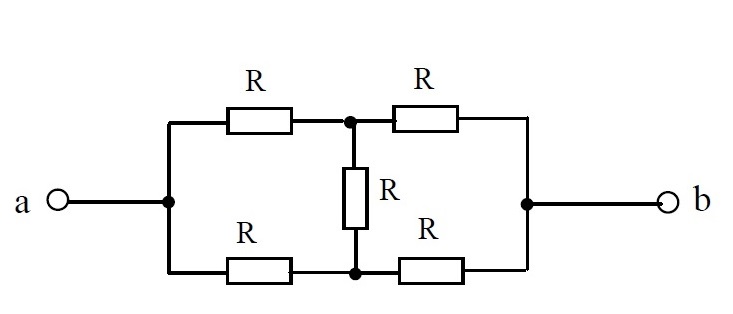
; ; .
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
; ; .
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
.
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке.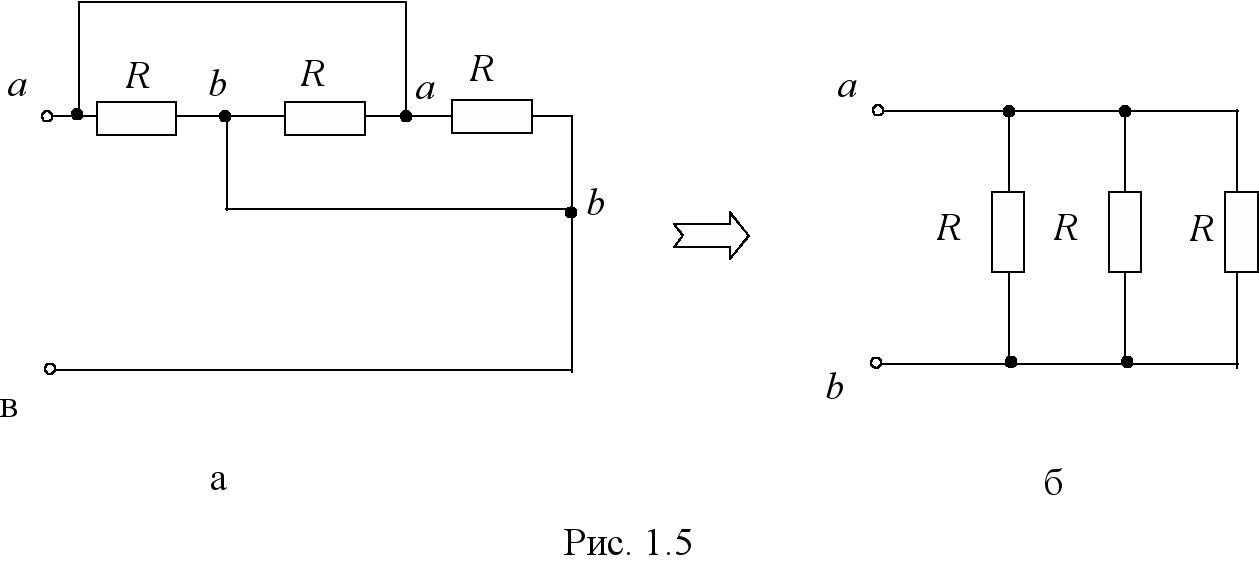
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ.
= Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент.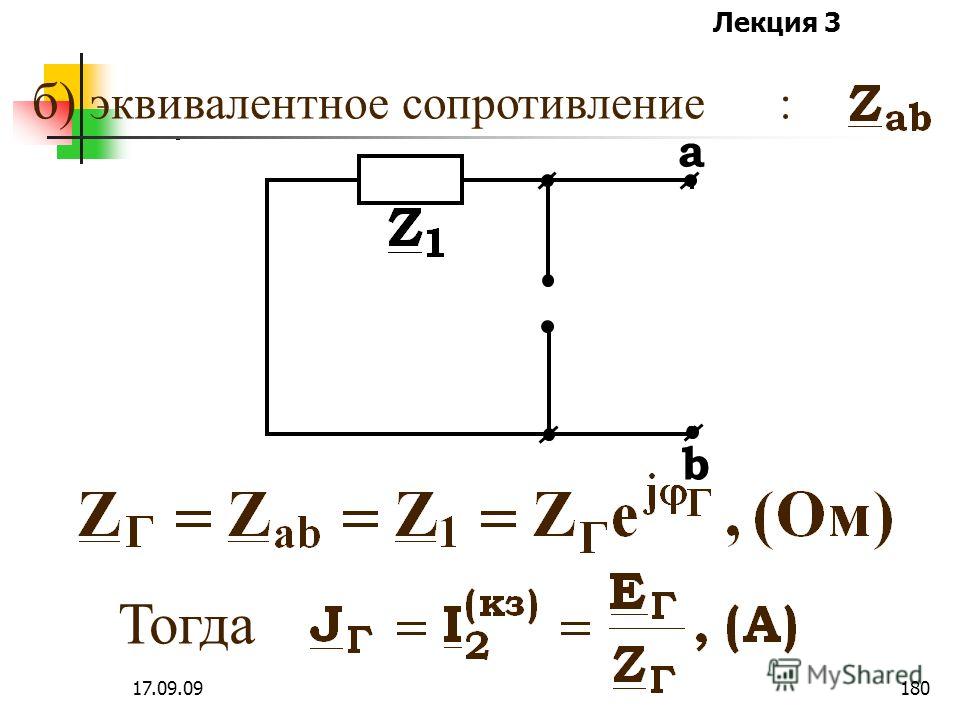
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв.
= (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание!
Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов.
Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
Физическая формула расчета (определения) эквивалентного сопротивления в цепи
Содержание
- 1 Последовательное соединение элементов
- 2 Параллельное соединение
- 3 Расчёт при смешанном соединении устройств
- 4 Видео
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.
Метод свёртывания цепи
Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Расчёт при смешанном соединении устройств
В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.
При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.
Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:
- R1 = 1Ом,
- R2 = 2Ом,
- R3 = 3Ом,
- R4 = 6Ом,
- R5 = 9Ом,
- R6 = 18Ом,
- R7 = 2,8Ом,
- U = 32В.
Электрическая схема
Из закона Ома имеем:
I = U/R,
где R – суммарное сопротивление всех приборов.
Его будем находить, воспользовавшись методом сворачивания цепи.
Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:
R2,3= R2·R3 / (R2+R3).
R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:
1/R4,5,6 = 1/R4+1/R5+1/R6.
Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.
Эквивалентная схема
Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.
Rобщ может быть найдено по формуле:
Rобщ = R1 + R2,3 + R4,5,6 + R7.
Подставляем числовые значения и рассчитываем R для определённых участков:
- R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
- 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
- R4,5,6 = 3Ом,
- Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.
Теперь, после того, как нашли Rэкв, можно вычислять значение I:
I = 32В / 8Ом = 4А.
После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.
Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:
I1 = I2,3 = I4,5,6 = I7 = I = 4А.
На участке R2,3 напряжение находим по формуле:
- U2,3 = I2,3·R2,3,
- U2,3 = 4А·1,2Ом = 4,8В.
Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:
- I2 = U2 / R2,
- I2 = 4,8В / 2Ом = 2,4А,
- I3 = U3 / R3,
- I3 = 4,8В / 3Ом = 1,6А.
Проверяем правильность решения:
- I2,3 = I2 + I3,
- I2,3 = 2,4А + 1,6А = 4А.
На участке R4,5,б напряжение также находим, исходя из закона Ома:
- U4,5,6 = I4,5,6·R4,5,6,
- U4,5,6 = 4А·3Ом = 12В.
Так как R4, R5, Rб подключены параллельно друг к другу, то:
U4,5,6 = U4 = U5 = U6 = 12В.
Вычисляем I4, I5, I6:
- I4 = U4 / R4,
- I4 = 12В / 6Ом = 2А,
- I5 = U5 / R5,
- I5 = 12В / 9Ом » 1,3А,
- I6 = U6 / R6,
- I5 = 12В / 18Ом » 0,7А.
Проверяем правильность решения:
I4,5,6 = 2А + 1,3А + 0,7А = 4А.
Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.
Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.
Видео
Общее сопротивление
Оцените статью:
Эквивалентное сопротивление — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты
170 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 Следующая →
AP Physics 1 Справка »
Электричество и волны »
Электричество »
Схемы »
Эквивалентное сопротивление
Рассмотрим следующую цепь:
Каково общее эквивалентное сопротивление цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала нам нужно уплотнить R3 и R4.
Теперь мы можем уплотнить R2 и R34. Они параллельны, поэтому мы будем использовать следующее уравнение:
Следовательно:
Эквивалентная схема теперь выглядит так:
Так как все последовательно, мы можем просто сложить все:
Сообщить об ошибке точка от А до Б?
Возможные ответы:
Правильный ответ:
Пояснение:
В новой схеме параллельно подключены два резистора: R2 и новый. Чтобы найти эквивалентное сопротивление этих двух ветвей, воспользуемся следующим выражением:
В этой новой эквивалентной схеме все последовательно, поэтому мы можем просто сложить сопротивления:
Теперь мы можем использовать закон Ома для расчета полного тока в цепи:
Сообщить об ошибке
Рассмотрим данную цепь:
Какое сопротивление должно быть приложено между точками A и B, чтобы в цепи был общий ток 3А?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы будем работать над этой задачей в обратном порядке, используя ток для нахождения сопротивления.
Мы знаем напряжение и требуемый ток, поэтому мы можем рассчитать общее необходимое сопротивление:
Затем мы можем рассчитать эквивалентное сопротивление двух резисторов, которые включены параллельно (R2 и наше неизвестное):
Теперь мы можем рассчитать, какое сопротивление между точкой A и B:
. Перестановка для желаемого сопротивления:
Отчет о ошибке
. Схема:
.
Если эквивалентное сопротивление цепи равно и каждый резистор одинаков, каково значение каждого резистора?
Возможные ответы:
Ни один из этих
Правильный ответ:
Объяснение:
Мы можем использовать уравнение для эквивалентного сопротивления параллельных резисторов, чтобы решить это уравнение:
Мы знаем эквивалентное сопротивление, и мы знаем, что сопротивление каждого из четырех резисторов равно:
Сообщить об ошибке
Рассмотрим схему:
Если мощность, рассеиваемая во всей цепи, равна , каково значение ?
Возможные ответы:
Правильный ответ:
Пояснение:
Зная мощность потерь и напряжение цепи, мы можем рассчитать эквивалентное сопротивление цепи, используя следующие уравнения:
Подставив закон Ома в уравнение для мощности, получим:0005
Переставляя сопротивления, получаем:
Это эквивалентное сопротивление всей цепи.
Сообщить об ошибке
Рассмотрим цепь:
Если ток, протекающий через цепь, каково значение R1?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем использовать закон OHM’s для расчета эквивалентного сопротивления схемы:
Теперь мы можем использовать выражение для объединения параллельных резисторов для расчета R1:
9000
9000
9000
Сообщить об ошибке
Рассмотрим схему:
Если эквивалентное сопротивление цепи равно , какая из следующих конфигураций значений сопротивления возможна?
Возможные ответы:
Ни один из этих ответов
Объяснение:
Нам нужно будет проверить значения каждого ответа, чтобы найти тот, который генерирует сопротивление, эквивалентное .
Мы знаем, что при соединении параллельных резисторов эквивалентное сопротивление никогда не будет больше наибольшего одиночного сопротивления и всегда будет меньше наименьшего сопротивления. Следовательно, два варианта ответа можно исключить сразу.
После того, как мы сузили наш выбор до других вариантов ответов, нам просто нужно проверить их по следующей формуле:
Сначала мы проверим неправильный ответ:
Теперь правильный ответ:
Сообщить об ошибке
Каково эквивалентное сопротивление от точки А до точки Б?
Возможные ответы:
Правильный ответ:
Пояснение:
Поскольку эта схема не является ни чисто последовательной, ни чисто параллельной, мы должны упростить ее, прежде чем решать. Замените правую ветвь, которая является чисто последовательной, ее эквивалентным сопротивлением:
Теперь у нас есть чисто параллельная цепь, каждая ветвь которой имеет сопротивление .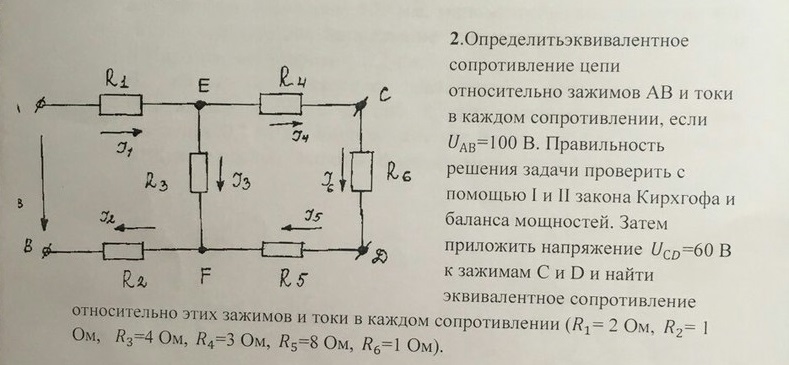
Сообщить об ошибке
Каково эквивалентное сопротивление следующих резисторов, соединенных последовательно: ?
Возможные ответы:
Правильный ответ:
Пояснение:
Для последовательно соединенных резисторов эквивалентное сопротивление равно сумме сопротивлений.
Сообщить об ошибке
Каково эквивалентное сопротивление цепи, состоящей из группы резисторов (соединенных параллельно) со следующими сопротивлениями: ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обратная величина эквивалентного сопротивления для параллельных резисторов равна сумме обратных величин сопротивлений:
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление
Все ресурсы AP Physics 1
7 Диагностические тесты
170 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Общая физика II
Вопросы 2, 4, 5, 6, 8, 9, 28
Проблемы 1, 2, 14, 15, 19, 20, 28, 41, 42, 45, 50
Q2 При каком условии разность потенциалов
на клеммах батареи равна ее ЭДС? Может ли терминал
напряжение когда-либо превышало ЭДС?
При отсутствии нагрузки напряжение на клеммах
то же, что и ЭДС.Напряжение на клеммах может никогда
превышать эдс.
Q4 Доступны два комплекта елочных огней. За
комплект А , при извлечении (или перегорании) одной лампочки
остальные лампочки продолжают гореть. Для комплекта B , когда один
лампочка удалена, остальные лампочки не работают. Объясните
разница в проводке двух наборов.
Набор А подключен параллельно.
Набор B соединен последовательно.
Q5 Как бы вы соединили резисторы, чтобы
эквивалентное сопротивление на больше, чем на
сопротивление?
Резисторы, включенные последовательно, обеспечат эквивалентную
сопротивление, превышающее наибольшую индивидуальную
сопротивление.
Q6 Как бы вы соединили резисторы, чтобы
эквивалентное сопротивление меньше чем физическое лицо
сопротивление?
Резисторы, включенные параллельно, обеспечивают эквивалент
сопротивление меньше, чем у наименьшего индивидуума
сопротивление.
Q8 Когда резисторы соединены последовательно , которые
из следующего будет тот же для каждого резистора:
разность потенциалов, ток, мощность?
Резисторы, соединенные последовательно, имеют общий ток.
Q9 Когда резисторы соединены параллельно ,
что из следующего будет таким же для каждого резистора:
разность потенциалов, ток, мощность?
Резисторы, включенные параллельно, имеют общее напряжение или
разность потенциалов.
Q28 Последовательная цепь состоит из трех одинаковых ламп
подключен к батарее, как показано на рис. 28.29. Когда переключатель S
закрыто, что происходит
(а) к силам света ламп А и В;
(б) к силе света лампы С;
(в) к току в цепи; а также
(г) к падению напряжения на трех лампах?
(e) Мощность, рассеиваемая в цепи, увеличивается или уменьшается
или остаться прежним?
Когда переключатель S замкнут, ток протекает через
сначала две лампочки, а затем течет через выключатель и обратно в
батарея.Третья лампочка гаснет.
(a) Лампы A и B (две слева) испытывают
полное напряжение вместо 2/3, поэтому их интенсивность
УВЕЛИЧИВАТЬ.(b) Яркость лампы C становится НУЛЕВОЙ.
(c) Ток УВЕЛИЧИВАЕТСЯ, так как эквивалентное сопротивление
контура теперь составляет всего 2/3 от того, что было до переключения
был закрыт.(d) Падение напряжения на каждой из ламп в начальный момент
было [(1/3) E] . После замыкания ключа напряжение
падение на каждой из первых двух ламп составляет [(1/20) E]
при этом напряжение на третьей лампе равно нулю.(e) Ток увеличивается, поэтому мощность тоже
УВЕЛИЧИВАЕТ.
28,1 Батарея с ЭДС 12 В и внутренней
сопротивление 0,90 Ом подключено через нагрузочный резистор R.
(a) Если ток в цепи равен 1,4 А, какова величина
Р?
(b) Какая мощность рассеивается на внутреннем сопротивлении
батарея?
I = 1,4 А = 12 В / [R + 0,90 ]
[R + 0,90]
= 12 В/1,4 А
Р + 0,90
= 8,57
R = (8,57 — 0,90)
R = 7,67
28,2 Батарея 9,00 В выдает 117 мА при подключении к
72,0 Ом Определить внутреннее сопротивление батареи.
0,117 А = 9,0 В / [72,0
+ Ринт]
[72,0
+ R целое число ] = 9,0 В / 0,117 А
72,0
+ R целое число = 76,9
R целое число = (76,9 — 72,0)
R целое число = 4,9
28,14 (a) Найдите эквивалентное сопротивление между точками
а и б на рисунке P28.14
(b) Если между точками приложена разность потенциалов 34 В
a и b, рассчитайте ток в каждом резисторе .
Сначала замените 7-
и 10-
резистор с одним эквивалентным резистором Req1. 7-
и 10-
резистор подключен в параллель:
1/R экв1 = 1/7
+ 1/10
1/R экв1 = (0,143 + 0,100)(1/)
1/R экв1 = 0,243 (1/)
R экв1 = (1/0,243
) = 4,12
Теперь эти три резистора входят в серию , поэтому мы можем
заменить их одним эквивалентным резистором Req2;
R экв2 = 4
+ 4.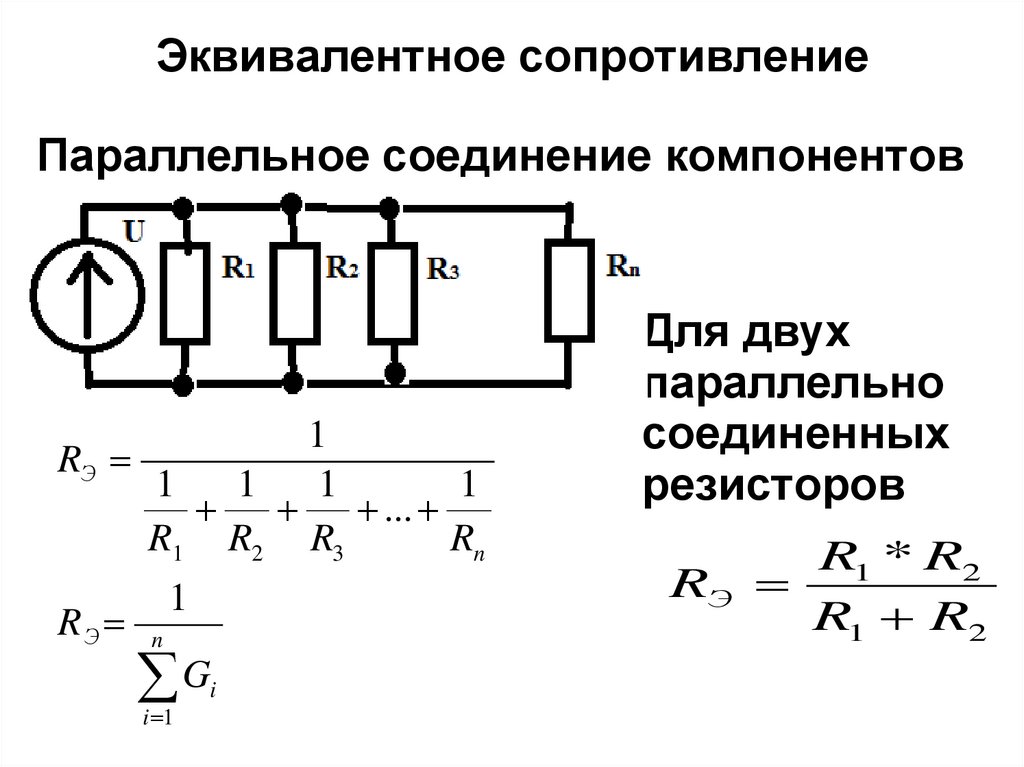
+ 9
Ч экв2 = 17,12
Теперь мы знаем эквивалентное сопротивление. Если разница в напряжении
34 В подается на клеммы a и b, ток
И = В/Р
I = 34 В / 17,12
I = 1,986 А
вытечет из аккумулятора. Этот же ток протекает через
4-
резистор и 9-
резистор. Тот же самый ток течет (или будет течь) через
первый эквивалентный резистор Req1. Это означает потенциал
разница между концами этого эквивалентного резистора Req1 должна быть
В = I R eq2
В = (1,986 А)(4,12 )
В = 8,18 В
Это напряжение также является общим напряжением на концах
7-
резистор и на концах 10-
резистор. Таким образом, мы можем найти ток через каждый из этих
резисторы;
И = В / Р
я(7)
= 8,18 В/7
= 1,17 А
Я(10)
= 8,18 В/10
= 0,82 А
Обратите внимание, что сумма из этих двух напряжений,
I Сумма = 1,17 А + 0,82 А = 1,99 А (по существу)
такой же, как ток через 4-
и 9-
резисторы (как это должно быть , конечно)!
28,15 Сопротивление между клеммами a и b на рис.
P28.15 — 75 Ом. Если резисторы с маркировкой R имеют одинаковое значение,
определить Р.
Сначала замените R и 5.0
с одним эквивалентным резистором R экв1 ,
Поскольку они входят в серию , этот эквивалентный резистор имеет
стоимость
R eq1 = R + 5,0
Теперь у нас есть три резистора параллельно .
Эти резисторы 120-
резистор, 40-
резистор, и этот эквивалентный резистор Req1 = R + 5,0 .
Рассчитайте этот новый эквивалентный резистор Req2, который заменит эти
три;
1/R eq2 = [1/120 + 1/40 + 1/(R +
5)][1/]
1/R экв2 = [0,00833 + 0,025 + 1/(R +
5)][1/]
1/R экв2 = [0,0333 + 1/(R +
5)][1/]
R eq2 = (1/[0,0333 + 1/(R + 5)])
Теперь у нас есть R и R eq2 в серии так что это
очень легко вычислить этот окончательный эквивалентный резистор, Req3;
R eq3 = R + R экв2
Это сопротивление равно 75 Ом.
Теперь мы можем использовать немного алгебры;
R экв.3 = R + R экв.2
R экв.2 = (1/[0,0333 + 1/(R + 5)])
75
= R + (1/[0,0333 + 1/(R + 5)])
28,19 Рассчитайте мощность, рассеиваемую на каждом резисторе в
схема рисунка П28.19.
Чтобы найти сила нам сначала нужно найти
ток через каждый резистор и напряжение через
каждый резистор. Это означает найти резистор , эквивалентный .
а затем возвращаемся обратно.
1/R экв1 = 1/3
+ 1/1
1/R экв1 = 4/3
R экв1 = (3/4)
R экв1 = 0,75
4
Теперь они в серии, поэтому мы можем заменить их окончательными
эквивалент резистора Треб.
Ч экв. = 2
+ 0,75
+ 4
R экв = 6,75
Ток, поступающий от аккумулятора,
I = V/R eq
I = 18 В / 6,75
I = 2,67 A
Это также ток через 2-
резистор и 4-
резистор.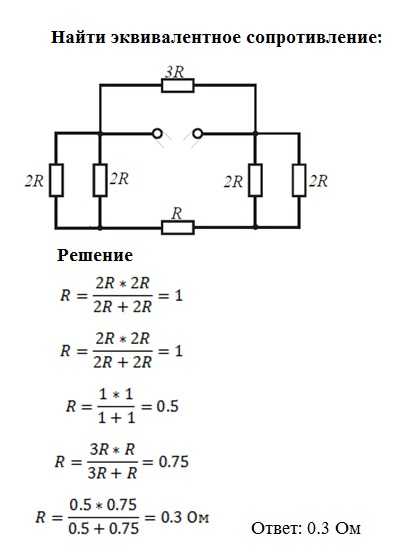
Р = I В = I 2 Р
P 2 = I 2 2 R 2
P 2 = (2,67 А) 2 (2 )
= 14,26 Вт
П 4 = И 4 2 Р
P 4 = (2,67 А) 2 (4 )
= 28,52 Вт
Мы можем легко найти напряжение на Req1, которое также является
напряжение на 1-
резистор и 3-
резистор.
В = I R eq1
В = (2,67 А) (0,75 Ом)
= 2,00 В
P = I V = (V/R) V = V 2 /Р
P 1 = (2 В) 2 /1
= 4 Вт
P 3 = (2 В) 2 /3
= 1,25 Вт
Теперь мы закончили. Но все же «приятно» проверить наши ответы или
проверить физику мощности, производимой батареей и
суммарная мощность, рассеиваемая всеми резисторами.
P bat = I В = (2,67 А)(18 В) = 48,06 Вт
P to = P1 + P2 + P3 + P4
P до = 4 Вт + 14,26 Вт + 1,25 Вт + 28,52 Вт
P до = 48,03 Вт
И те же (с точностью до «ошибки округления»), что и
должно быть.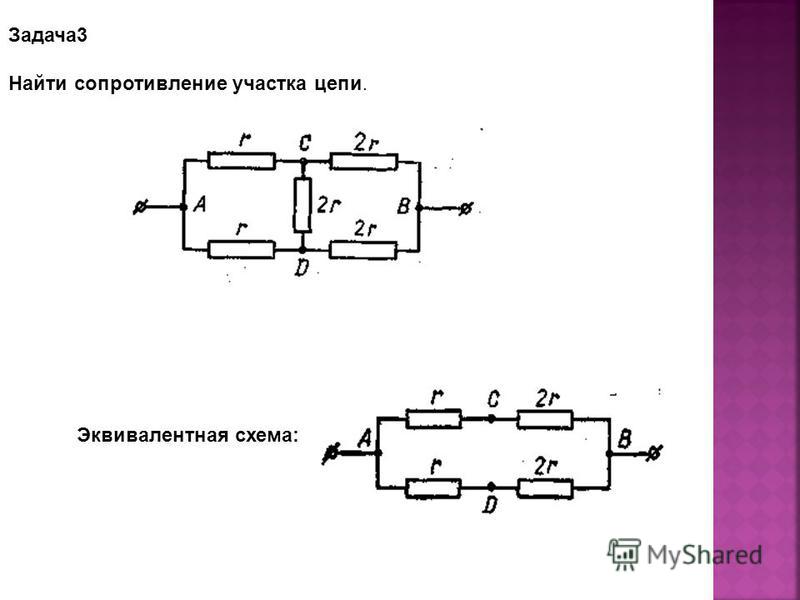
28,20 Определите эквивалентное сопротивление между
клеммы a и b для сети, показанной на рисунке P28.20.
Три резистора в правом нижнем углу находятся в
параллель . Иногда помогает просто перерисовать а
схема.
Перерисовал вот так, должно быть понятно, что три резистора
в правом нижнем углу параллельны . Начнем с
заменив их эквивалентным резистором R eq1 .
1/R экв1 = 1/2
+ 1/2
+ 1/1
1/R экв1 = (0,5 + 0,5 + 1,0)(1/)
1/R экв1 = 2,0 (1/)
Ч экв1 = 0,5
Ч экв2 = 2,0
+ 0,5
R экв2 = 2,5
Теперь обратим внимание на 3.0-
и 5.0-
резисторы в верхней части схемы, которые подключены в
параллели.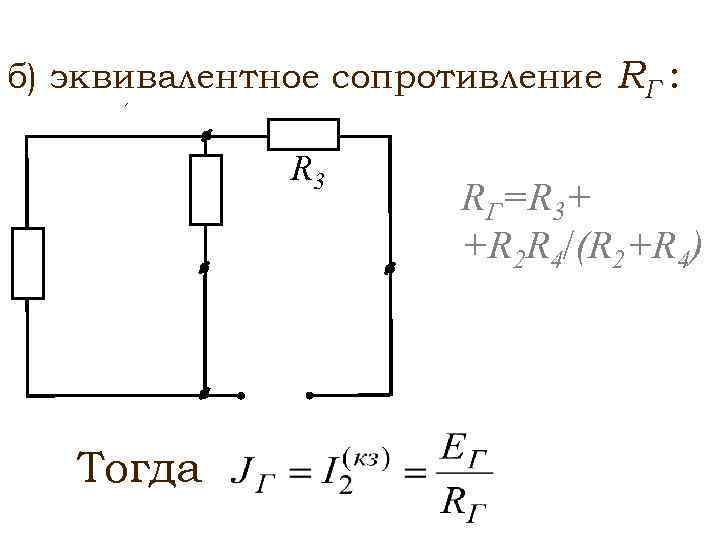
1/R экв3 = 1/3
+ 1/5
1/R экв3 = (0,33 + 0,20)(1/)
1/R экв3 = 0,53 (1/)
R EQ3 = (1/0,53)
R EQ3 = 1,89
R EQ4 = R EQ3 + 1,1
999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999979н.
+ 1,0
R EQ4 = 2,89
1/R EQ5 = 1/R EQ4 + 1/R EQ2
741574747475759575757575757575757575757575757575757575757575757575757575757575757575757575757575757575749тели + 1/R .
+ 1/2,5
1/R экв5 = (0,346 + 0,4)(1/)
1/Р экв5 = 0,746 (1/)
R экв5 = (1/0,746)
R экв5 = 1,34
R экв = 2,0575
+ R экв5
R экв = 2,0
+ 1,34
R экв = 3,34
R экв = 3,34
28,28 В схеме рисунка Р28.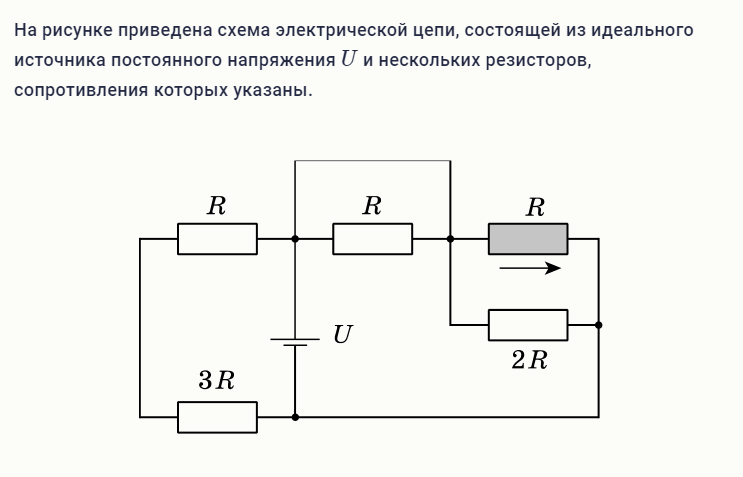
ток в каждом резисторе и напряжение на 200-омной
резистор.
Хорошо, вот оно! Это требует применения
Правила Кирхгофа . Начните с назначения тока через каждый
резисторов.
Применить Кирхгофа Правило соединения к двум соединениям.
J1: I 1 +
I 2 = I 5
J2: I 5 +
Я 3 + Я 4 = 0
I 1 + I 2 + I 3 + I 4 =
0
Безусловно, один или несколько наших токов окажутся
минус . (Это хорошо! ) У нас есть четыре
неизвестные и только одно уравнение. Нам нужно будет получить три
больше уравнений из правила цикла Кирхгофа.
L1: — 40 В = I 2
(80 )
— я 1 (200 )
L2: 40 В — 360 В =
I 3 (20 )
— I 2 (80 )
L3: — 360 В — 80 В =
I 4 (70 )
— Я 3 (20)
Мы закончили с «Физикой» этой задачи.
Это
«просто» математика с этого момента. У нас есть четыре неизвестных так что теперь
нам нужно всего четыре уравнения ,Я 1 + Я 2 + Я 3 +
I 4 = 0— 40 В = I 2 (80 )
— I 1 (200 )40 В — 360 В = I 3 (20 )
— I 2 (80 )— 360 В — 80 В = I 4 (70 )
— I 3 (20 )80 В = I 4 (70 )
— I 1 (200 )
Принятие решения о выборе «петли» иногда кажется трудным.
Любая непрерывная петля является кандидатом. Мы могли бы использовать
петля вокруг снаружи всей принципиальной схемы.L4: 80 В = I 4
(70 )
— I 1 (200 )
28,41 Полностью заряженный конденсатор хранит 12 Дж энергии.
Сколько энергии останется, когда его заряд уменьшится до половины своего
исходное значение?
Э =
( 1 / 2 )
Q 2 / С
Когда груз уменьшается до половины , энергия
уменьшилось до четверти .
28,42 Рассмотрим последовательную RC-цепь (рис. 28.15) для
где R = 1,0 МОм, C = 5,00 мкФ и E = 30,0 В. Найти
(а) постоянная времени цепи и
(b) максимальный заряд конденсатора после переключения
закрыто.
в) Если ключ замкнут в момент времени t = 0, найти ток в
резистор через 10,0 с.
(а) постоянная времени цепи
= Р С
=
(1 x 10 6 )(5 x 10 — 6 ) с
=
5 с
(b) максимальный заряд конденсатора после переключения
закрыто.
С = Q/V
Q f = C V
Q f = (5 x 10 — 6 f)(30 В)
[ (В/П) / ф ]
Q f = 0,00015 С
Q f = 1,5 x 10 — 4 C
(в) Если ключ замкнут в момент времени t = 0, найти ток в
резистор через 10,0 с.
Io = V/R = 30 В/1 x 10 6
Io = 3 x 10 — 5 A
I(5 с) = (3 x 10 — 5 A) EXP[ — (5 с/10 с)]
I(5s) = (3 x 10 — 5 A) EXP[ — 2]
I(5s) = (3 x 10 — 5 А) (0,135)
I(5s) = 4,05 x 10 — 6 А
I(5 с) = 4,05 А
28,45 Резистор 4,00 МОм и 3,00 мкФ
Конденсатор соединен последовательно с источником питания 12,0 В.
а) Какова постоянная времени цепи?
(b) Выразите ток в цепи и заряд на
конденсатор как функция времени.
= Р С
=
(4 x 10 6 )(3 x 10 — 6 ) с
=
12 с
Io = V/R = 12 В/4 x 10 6
Io = 3 x 10 — 6 A
Io = 3 А
i(t) = (3 А)
ОПЫТ(- т/12с)
С = Q/V
Q f = C V
Q f = (3 x 10 — 6 f)(12 В)
[(С/В)/ф]
Q f = 36 х 10 — 6 С
Q f = 36 С
q(t) = (36 С)
[ 1 — ОПЫТ (- t/12s)
28,50 Конденсатор в RC-цепи заряжается до 60 %
его максимальное значение через 0,90 с.
Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
Электрическая
цепь с последовательным соединением
элементов
|
|
|
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1.5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
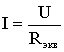
и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая
цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
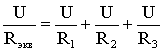
откуда
следует, что
(1.6)
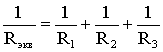
В
том случае, когда параллельно включены
два сопротивления R1
и R2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
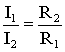
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
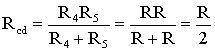
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
Рис.
1.9
На
схеме (рис. 1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
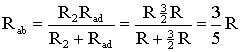
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
.
|
|
|
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
по мостовой схеме (рис. 1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
|
|
|
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1.8)

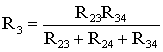
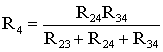
Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
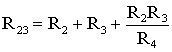
;
.
После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
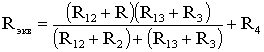
Главная > Теория > Эквивалентное сопротивление
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.
Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие “блок”. Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.
В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема – это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод “от простого к сложному” полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем – готовое устройство, например, телевизор.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
– Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление – это сопротивление какого-то входа, а выходное – сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот “прячутся” они в самих блоках радиоэлектронных устройств.
Расчёт при смешанном соединении устройств
В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.
При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.
Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:
- R1 = 1Ом,
- R2 = 2Ом,
- R3 = 3Ом,
- R4 = 6Ом,
- R5 = 9Ом,
- R6 = 18Ом,
- R7 = 2,8Ом,
- U = 32В.
Из закона Ома имеем:
I = U/R,
где R – суммарное сопротивление всех приборов.
Его будем находить, воспользовавшись методом сворачивания цепи.
Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:
R2,3= R2·R3 / (R2+R3).
R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:
1/R4,5,6 = 1/R4+1/R5+1/R6.
Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.
Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.
Rобщ может быть найдено по формуле:
Rобщ = R1 + R2,3 + R4,5,6 + R7.
Подставляем числовые значения и рассчитываем R для определённых участков:
- R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
- 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
- R4,5,6 = 3Ом,
- Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.
Теперь, после того, как нашли Rэкв, можно вычислять значение I:
I = 32В / 8Ом = 4А.
После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.
Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:
I1 = I2,3 = I4,5,6 = I7 = I = 4А.
На участке R2,3 напряжение находим по формуле:
- U2,3 = I2,3·R2,3,
- U2,3 = 4А·1,2Ом = 4,8В.
Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:
- I2 = U2 / R2,
- I2 = 4,8В / 2Ом = 2,4А,
- I3 = U3 / R3,
- I3 = 4,8В / 3Ом = 1,6А.
Проверяем правильность решения:
- I2,3 = I2 + I3,
- I2,3 = 2,4А + 1,6А = 4А.
На участке R4,5,б напряжение также находим, исходя из закона Ома:
- U4,5,6 = I4,5,6·R4,5,6,
- U4,5,6 = 4А·3Ом = 12В.
Так как R4, R5, Rб подключены параллельно друг к другу, то:
U4,5,6 = U4 = U5 = U6 = 12В.
Вычисляем I4, I5, I6:
- I4 = U4 / R4,
- I4 = 12В / 6Ом = 2А,
- I5 = U5 / R5,
- I5 = 12В / 9Ом » 1,3А,
- I6 = U6 / R6,
- I5 = 12В / 18Ом » 0,7А.
Проверяем правильность решения:
I4,5,6 = 2А + 1,3А + 0,7А = 4А.
Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.
Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.
Что такое эквивалентное сопротивление резисторов
Точного понятия в физике не существует. Его можно вывести через ряд других терминов и формулировку закона Ома. В результате получится, что эквивалентное сопротивление резисторов — это суммарное препятствие взаимозаменяемых пассивных элементов электрической сети, чтобы заряд проходил в проводник.
К сведению! Один показатель дает на выходе значение сопротивляемости без воздействия на него ряда посторонних моментов.
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда » в эквивалентный «треугольник » и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Полезная информация для начинающего электрика
Как использовать закон Ома на практике
Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.
Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.
Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.
Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:
- значения приложенного к цепи напряжения;
- сопротивления среды, по которой движется ток.
Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.
Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.
Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.
Как определить эквивалентное сопротивление
Если в электрической сети находится несколько резистивных источников, то, чтобы подсчитать силу тока, напряжения и мощность, следует использовать один взаимозаменяемый физический показатель сопротивления электрической цепи.
Любой показатель последовательного или параллельного подключения возможно преобразовать, используя эквивалентный резистор и один источник электродвижущей силы. Сопротивляемость в данном случае будет равна сумме всех препятствий пассивных устройств заряду электрической сети. Электродвижущая сила взаимозаменяемого источника будет равна сумме всех источников, которые входят в цепь.
Обратите внимание! Сворачиванием цепи, используя преобразования последовательно подключенных или параллельных проводниковых приборов, можно по максимуму сделать проще дальнейший расчет в любой схеме. Исключением будут выступать цепи, которые содержат сопротивляемость по схеме в виде звезды и треугольника.

.png)
.png)
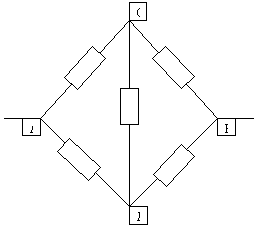
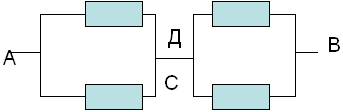
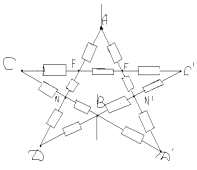
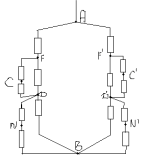
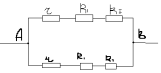
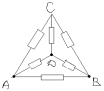
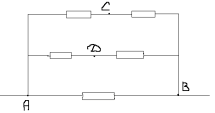
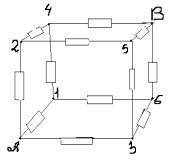
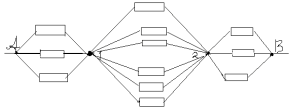
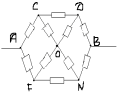
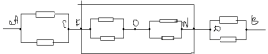
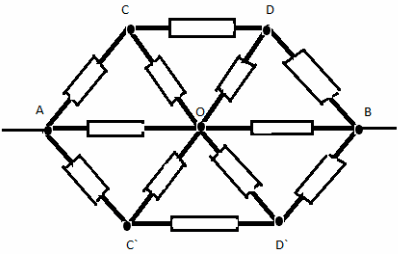
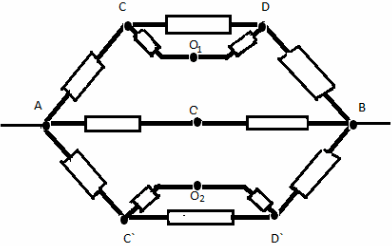
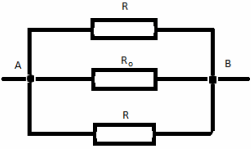
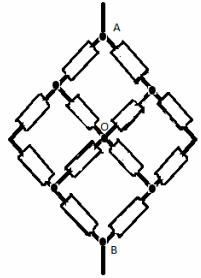
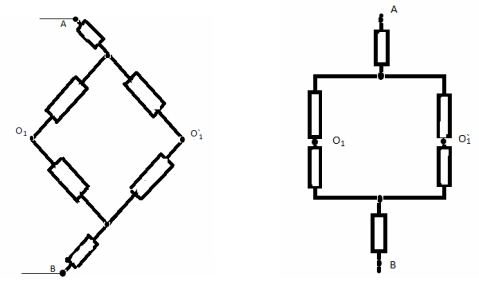
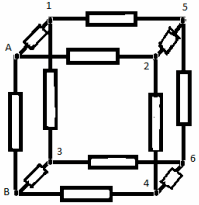
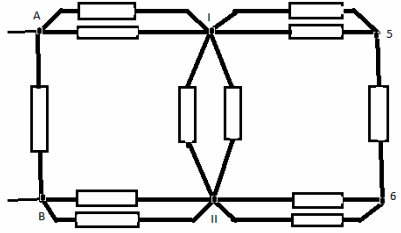
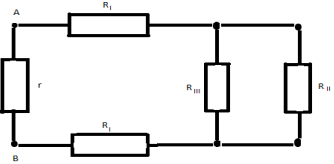
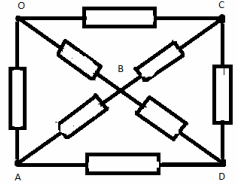
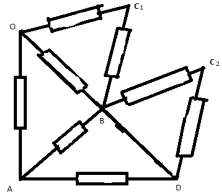
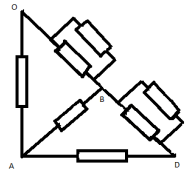
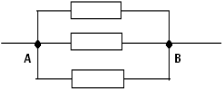
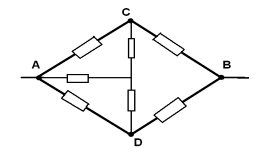
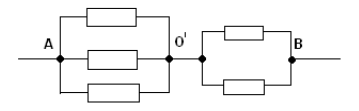
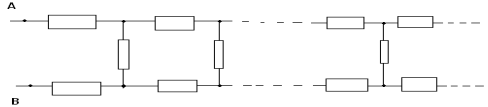
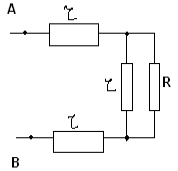
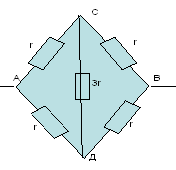
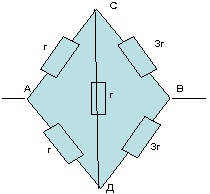
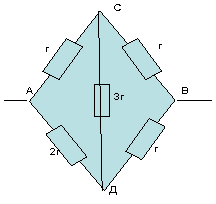
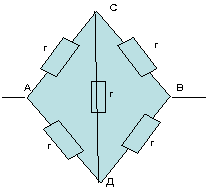
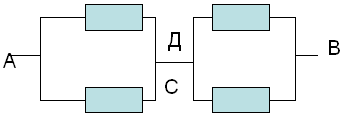

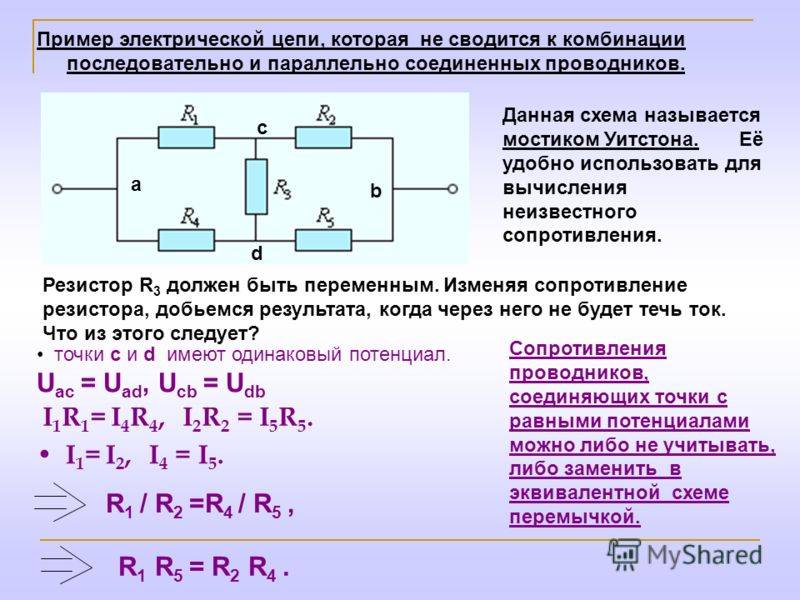 = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
= Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.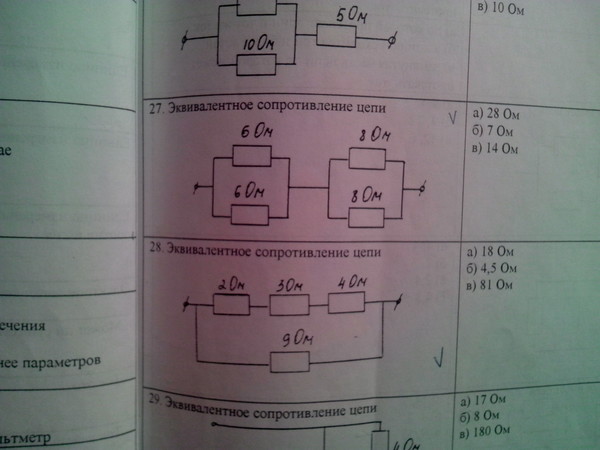 = (R1*R2)/R1+R2;
= (R1*R2)/R1+R2;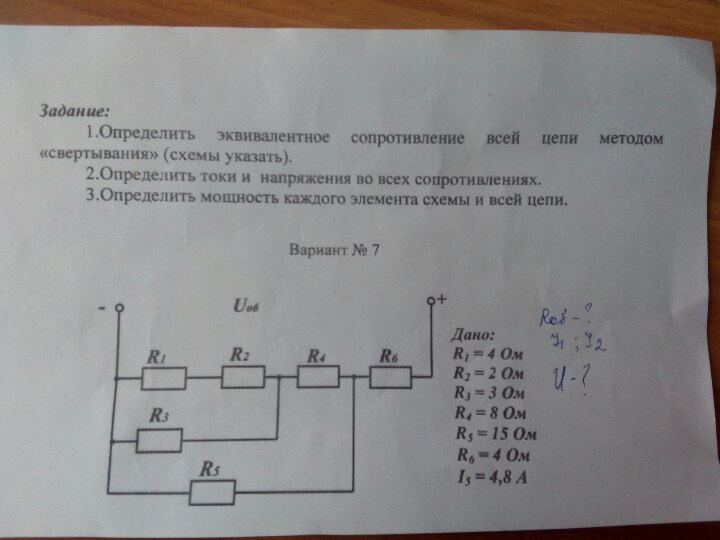
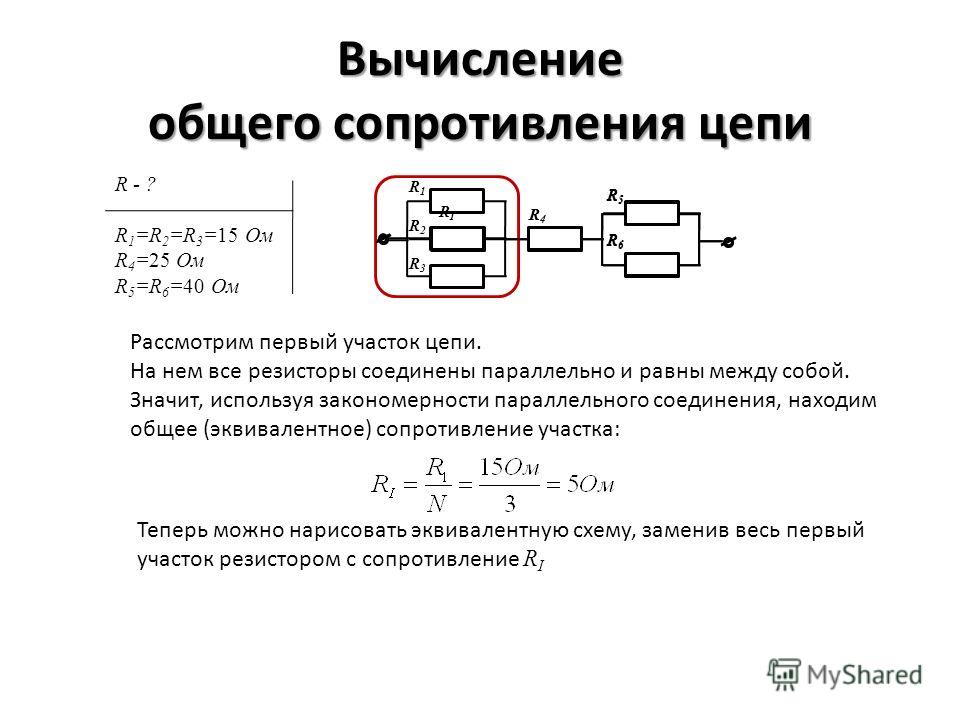



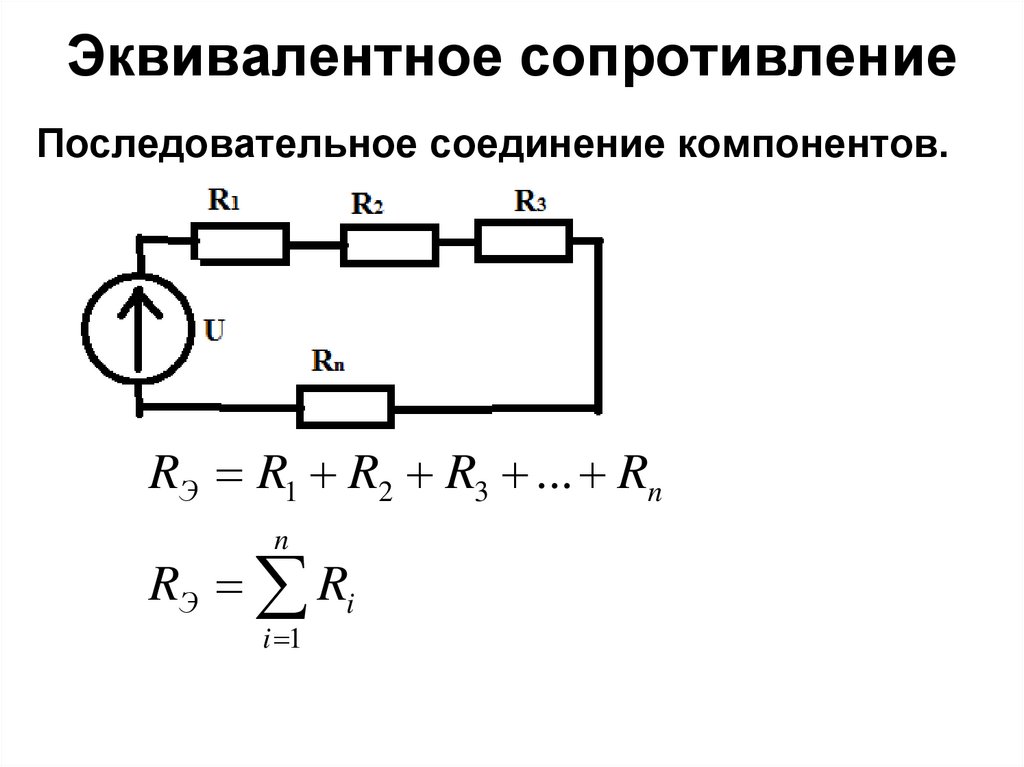
 Напряжение на клеммах может никогда
Напряжение на клеммах может никогда 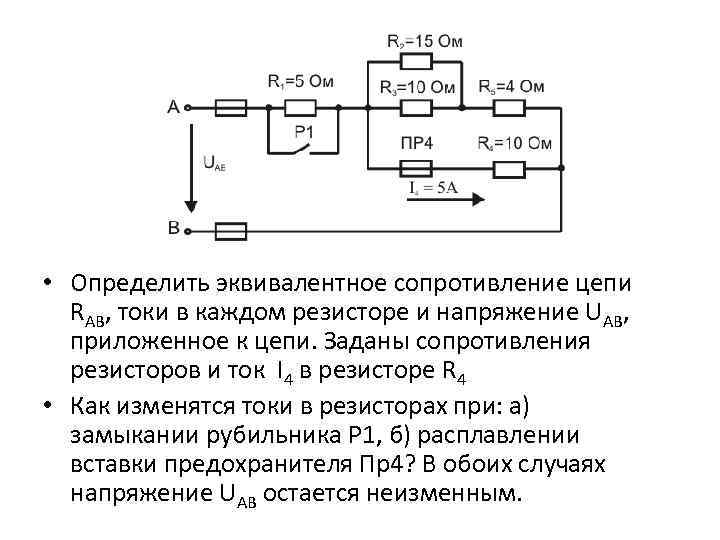
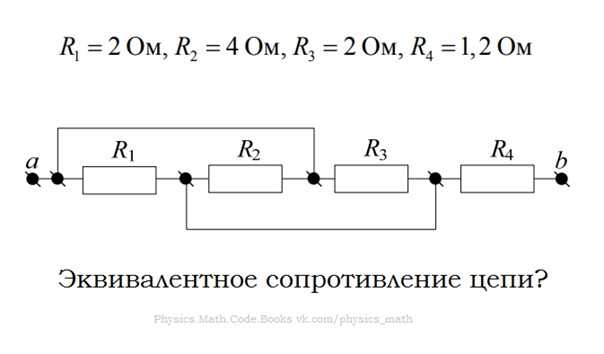 Третья лампочка гаснет.
Третья лампочка гаснет. 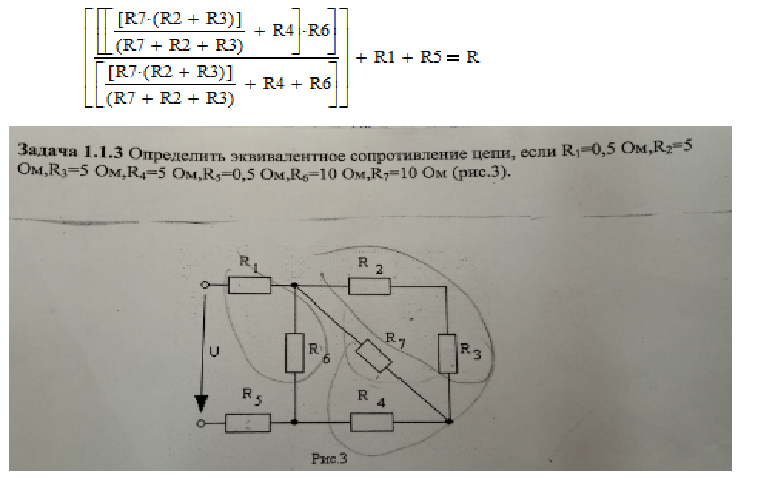

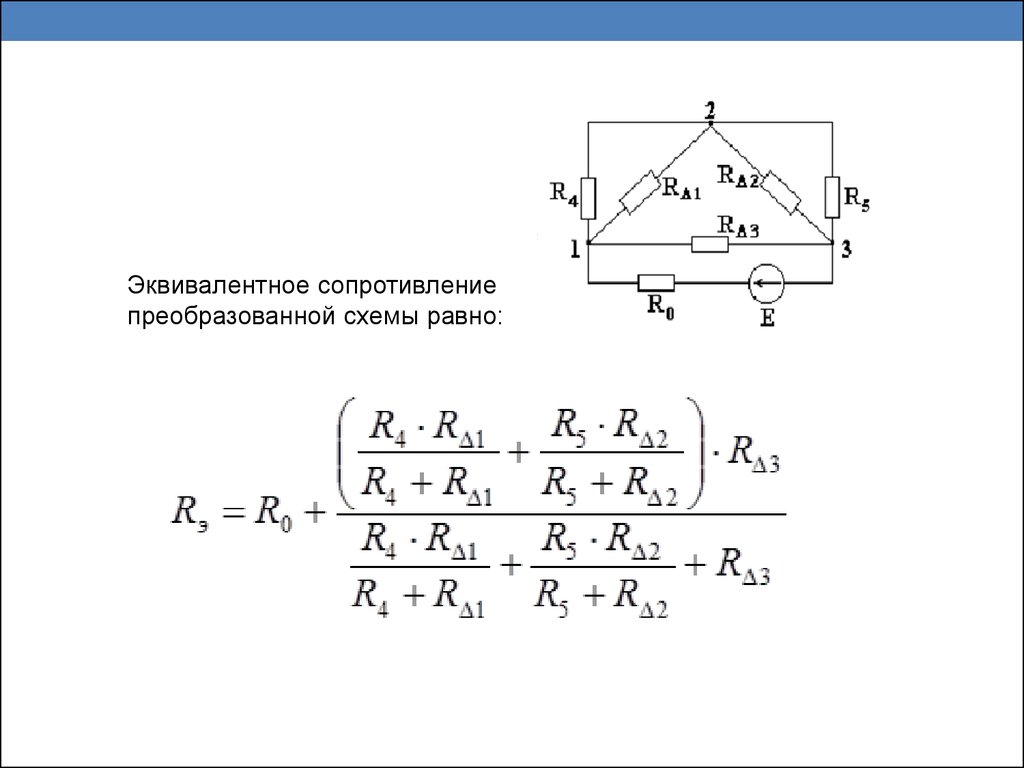 Это
Это