Как найти результирующую скорость

Physics can be a challenging course for anyone because it combines science with math and introduces potentially difficult concepts. One basic idea is the concept of speed and how it changes. Calculating the speed of an object can be a simple process if a few basic rules are kept in mind. Learn how to solve problems where you need to find the resultant velocity.

Find Acceleration

First, make sure all the units are in standard form before doing any calculations. Write down all the information you need before starting your calculations and then draw a picture of the problem to help you understand what is going on. Find the acceleration of the object, the time the object is being accelerated and the initial velocity. These values are usually given to you in the problem. If the force is given, find the acceleration by dividing the force on the object by its mass.

Convert Units

Convert all units to standard units of measurement. Acceleration should be in meters per second squared. Velocity should be in meters per second and time should be in seconds.

Resultant Velocity

Multiply the acceleration by the time the object is being accelerated. For example, if an object falls for 3 seconds, multiply 3 by 9.8 meters per second squared, which is the acceleration from gravity. The resultant velocity in this case is 29.4 meters per second.

Velocity Formula

Add this velocity to the initial velocity. In the example above, if the object had an initial velocity of 5 meters per second, the resultant velocity would be 34.4 meters per second. The overall formula here is v (final) — at + v (initial) where «v» is velocity, «a» is acceleration and «t» is time. In this example the equation would look like this: v (final) = 9.8 x 3 + 5, giving us a result of 34.4.

After Impact

Identify the initial velocity of the two objects, the mass of both objects and the final speed of either object if it is given. These values are usually given in the problem. Convert all velocities to meters per second and all masses to kilograms.

Multiply Velocity by Mass

Multiply the initial velocity of each object by its mass. Add these two products together to get the total momentum. For example, if both objects have a mass of 5 kilograms, one is at rest and the other is moving at 10 meters per second. The calculation would look like this: 5 x 10 + 5 x 0. This would give us a result of 50 kilogram-meters per second.

Determine Final Velocity

Divide the total momentum by the sum of the masses if the two objects stick together after impact. This will give you the resultant velocity of the two objects. In the example above, we would take 50 and divide by the sum of the masses, which is 10, getting a result of 5 meters per second. If the objects do not stick together, subtract the product of the mass and the final velocity of one object from the total initial momentum. Then, divide the difference by the mass of the other object. This will give you the resultant velocity of the other object. In the example from the previous step, if the final velocity of the object originally moving at 10 meters per second was 2 meters per second, our calculation would look like this: (50 — 10) / 5, which gives us a result of 8 meters per second.

Физика может быть сложным курсом для любого, потому что она сочетает в себе науку с математикой и вводит потенциально сложные понятия. Одной из основных идей является концепция скорости и как она меняется. Расчет скорости объекта может быть простым процессом, если учитывать несколько основных правил. Узнайте, как решать проблемы, где вам нужно найти результирующую скорость.

Найти ускорение

Во-первых, убедитесь, что все единицы в стандартной форме, прежде чем делать какие-либо вычисления. Запишите всю необходимую информацию, прежде чем начинать свои вычисления, а затем нарисуйте картину проблемы, чтобы помочь вам понять, что происходит. Найти ускорение объекта, время ускорения объекта и начальную скорость. Эти значения обычно даются вам в задаче. Если сила дана, найдите ускорение, разделив силу на объекте на его массу.

Конвертировать единицы

Перевести все единицы в стандартные единицы измерения. Ускорение должно быть в метрах в секунду в квадрате. Скорость должна быть в метрах в секунду, а время в секундах.

Результирующая скорость

Умножьте ускорение на время ускорения объекта. Например, если объект падает в течение 3 секунд, умножьте 3 на 9, 8 метра в секунду в квадрате, что является ускорением от силы тяжести. Результирующая скорость в этом случае составляет 29, 4 метра в секунду.

Формула скорости

Добавьте эту скорость к начальной скорости. В приведенном выше примере, если бы начальная скорость объекта составляла 5 метров в секунду, результирующая скорость составила бы 34, 4 метра в секунду. Общая формула здесь v (окончательная) — при + v (начальная), где «v» — скорость, «a» — ускорение, а «t» — время. В этом примере уравнение будет выглядеть так: v (окончательный) = 9, 8 х 3 + 5, что дает нам результат 34, 4.

После удара

Определите начальную скорость двух объектов, массу обоих объектов и конечную скорость любого объекта, если она задана. Эти значения обычно приведены в задаче. Переведите все скорости в метры в секунду, а все массы в килограммы.

Умножьте скорость на массу

Умножьте начальную скорость каждого объекта на его массу. Добавьте эти два продукта вместе, чтобы получить общий импульс. Например, если оба объекта имеют массу 5 кг, один находится в покое, а другой движется со скоростью 10 метров в секунду. Расчет будет выглядеть так: 5 х 10 + 5 х 0. Это даст нам результат 50 килограмм-метров в секунду.

Определить конечную скорость

Разделите общий импульс на сумму масс, если два объекта слиплись после удара. Это даст вам результирующую скорость двух объектов. В приведенном выше примере мы возьмем 50 и разделим на сумму масс, которая равна 10, получая результат 5 метров в секунду. Если объекты не слипаются, вычтите произведение массы и конечной скорости одного объекта из общего начального импульса. Затем разделите разницу на массу другого объекта. Это даст вам результирующую скорость другого объекта. В примере из предыдущего шага, если конечная скорость объекта, первоначально движущегося со скоростью 10 метров в секунду, составляла 2 метра в секунду, наш расчет будет выглядеть следующим образом: (50 — 10) / 5, что дает нам результат 8 метров в секунду.

Решение задач на тему:

Относительное движение и сложение скоростей

1. Относительное движение в одном направлении

По шоссе движется перевозчик со скоростью 13 м/с. В том же направлении движется другой перевозчик со значением скорости, равным 12,2 м/с. В ответе запиши , с какой скоростью по модулю движется первый перевозчик относительно другого.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=13 м/с;

∣V⃗₂∣=12,2 м/с;

∣V⃗∣−?

Чтобы найти, с какой скоростью по модулю первый перевозчик движется относительно другого, необходимо заметить, что они оба движутся в одном направлении.

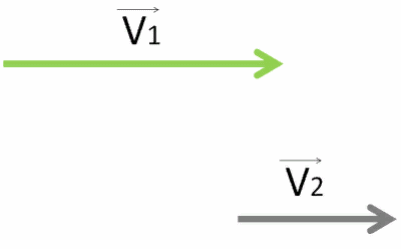
Найти скорость, с которой первый перевозчик движется относительно другого, очень просто.

Нужно отнять от его вектора скорости V⃗₁ вектор V⃗₂ , с которой движется другой перевозчик.

Чтобы это сделать, нужно к вектору V⃗₁ прибавить вектор V⃗₂, только поменяв его направление.

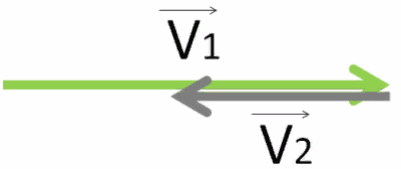
Результирующий вектор V⃗ получим, соединив начало первого вектора с концом последнего.

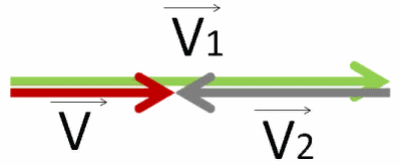
Получим вектор V⃗ красного цвета.

Чтобы найти его числовое значение, нужно от числового значения вектора V⃗₁ отнять числовое значение вектора V⃗₂ и результат взять по модулю.

Получим:

|V|=|13−12,2| = 0,8 м/с.

2. Относительная скорость тел, движущихся под прямым углом друг к другу

По свежеположенной дороге перемещается гусеничный трактор , имея скорость 6,3 км/ч. Перпендикулярно движется другой гусеничный трактор со скоростью 8,2 км/ч. Найди значение модуля скорости, с которой движется первый гусеничный трактор относительно другого.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=6,3 км/ч;

∣V⃗₂∣=8,2 км/ч;

∣V⃗ ∣−?

Как мы видим, первый гусеничный трактор движется под углом 90 градусов к другому.

Покажем направления их скоростей с помощью векторов V⃗₁ и V⃗₂.

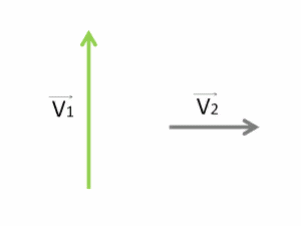
Чтобы найти скорость, с которой движется первый гусеничный трактор относительно другого, необходимо векторно от скорости первого V⃗₁ отнять скорость второго V⃗₂.

Отнимание вектора V⃗₂ проще заменить сложением вектора, противоположного ему: −V⃗₂.

Получим:

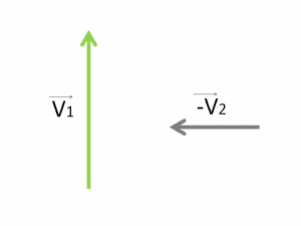
Чтобы найти результирующую скорость V⃗ , необходимо векторно сложить векторы V⃗₁ и −V⃗₂ . Для интереса попробуем это сделать двумя способами.

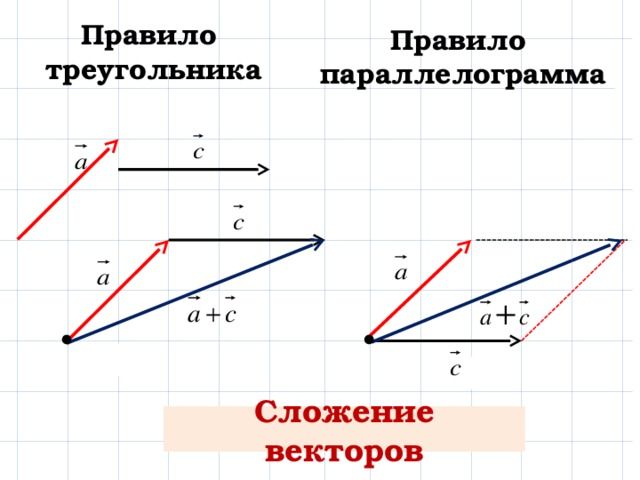
Выстраиваем их друг за другом, чтобы получились стороны треугольника.

Или соединяем начала этих векторов — тогда будем использовать правило параллелограмма.

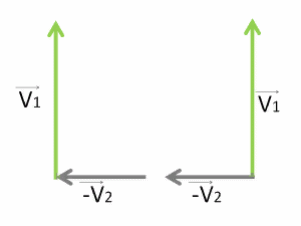
Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Должен получиться один и тот же вектор V⃗ . Изобразим его красным.

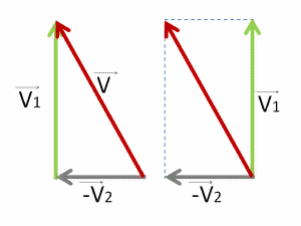
Результат сложения не зависит от выбора правила сложения — по правилу треугольника или параллелограмма.

Как видно, у нас получился прямоугольный треугольник со сторонами V⃗₁ , −V⃗₂ , V⃗ .

По условию задачи нам известны две его стороны, это два катета:

∣V⃗₁∣=6,3 км/ч и ∣−V⃗₂∣=8,2 км/ч.

Используя теорему Пифагора, мы можем найти гипотенузу V⃗:

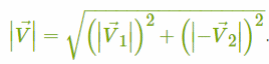
Численно получим:

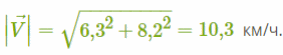
3. Относительная скорость течения реки

Величина скорости пловца вверх по течению реки относительно припаркованного возле магазина мотоцикла — 28,5 км/ч, а вниз по реке — 32,9 км/ч.

Напиши , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

V_po=32,9 км/ч;

V_pro=28,5 км/ч;

V⃗₂−?

Попробуем представить себе, как движется пловец по течению. Если обозначить эту скорость V⃗₁, а течение реки V⃗₂, то, скорее всего, это будет выглядеть так:

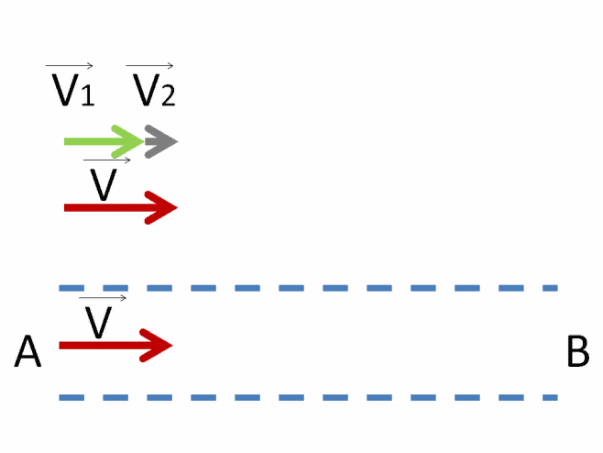
Как видно, результирующий вектор V⃗ получился равным сумме векторов V⃗₁ и V⃗₂ .

Именно с такой скоростью движется пловец по течению.

Если показывать движение пловца против течения, то с теми же обозначениями получим:

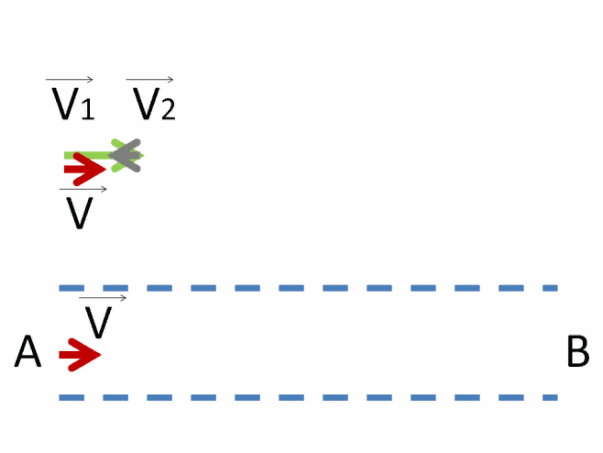
Как видно, уже в этом случае результирующий вектор скорости пловца V⃗ стал меньше, т.к. он равен разности векторов V⃗ 1 и V⃗ 2 . Оно и понятно, ведь против течения двигаться сложнее, скорость пловца меньше из-за встречного течения воды.

Это хорошо, что мы представили себе эту задачу. Но чтобы её решить, нужно составить уравнения движения по течению и против течения реки:

V₁+V₂=32,9;

V₁−V₂=28,5.

В математике это называется системой уравнений.

Не забывай, что найти нам нужно , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, т.е. V⃗₂.

Попробуем выразить её из первого уравнения. Для этого V⃗₁ перенесётся в правую сторону и поменяет знак:

V₂=32,9−V₁.

Как видно, найти значение V₂ мы пока не можем, т.к. не знаем скорости пловца V₁.

Но для этого нам дано второе уравнение в системе.

Выразим его оттуда.

Получим:

V₁=28,5+V₂.

Нам нужно подставить вместо обозначения V₁ его значение 28,5+V₂ в уравнение:

V₂=32,9−V₁.

Получим:

V₂=32,9−(28,5+V₂);

V₂=32,9−28,5−V₂;

V₂=4,4−V₂;

2V₂=4,4;

V₂=2,2.

В итоге , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, мы узнали — 2,2 км/ч.

4. Нахождение времени переплывания реки при движении перпендикулярно к течению реки

Лайнер, двигаясь под углом 90 градусов к течению реки , обладая скоростью 4,3 м/с, переплывает реку шириной 370 м. Скорость течения реки — 2,1 м/с. В ответе укажи время, нужное лайнеру , чтобы переплыть реку.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=4,3 м/с;

∣V⃗₂∣=2,1 м/с;

|S|=370 м;

|t|−?

Обозначим скорость лайнера V⃗₁, а скорость течения реки V⃗₂.

Покажем на рисунке, как направлены векторы их скоростей.

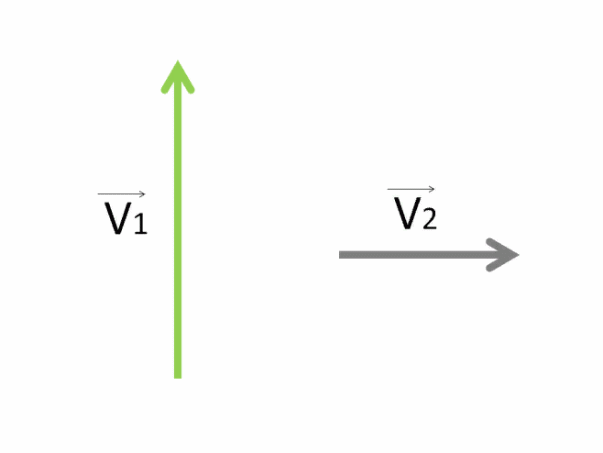
Естественно, лайнер не сможет уже плыть прямо. Течение реки будет действовать вправо и лайнер начнёт смещаться понемногу в ту сторону, куда оно направлено.

Можно показать, конечно, как точно будет направлен результирующий вектор скорости.

Для этого нужно сложить скорости V⃗₁ и V⃗₂ по правилу треугольника или по правилу параллелограмма.

Правильно это сделать так:

выстраиваем их друг за другом, чтобы получились стороны треугольника

или соединяем начала этих векторов — тогда используем правило параллелограмма.

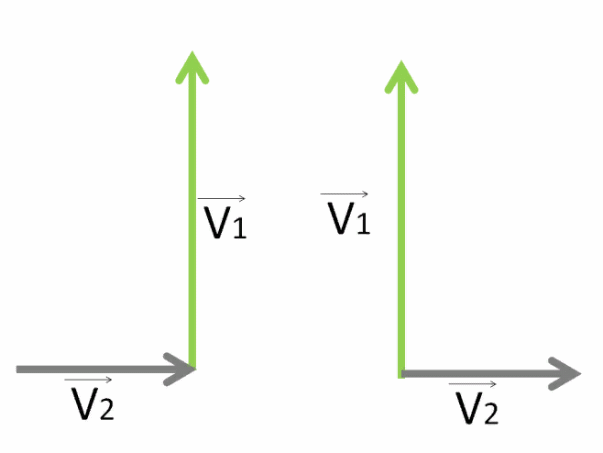
Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Должен получиться один и тот же вектор V⃗ . Нарисуем его красным цветом.

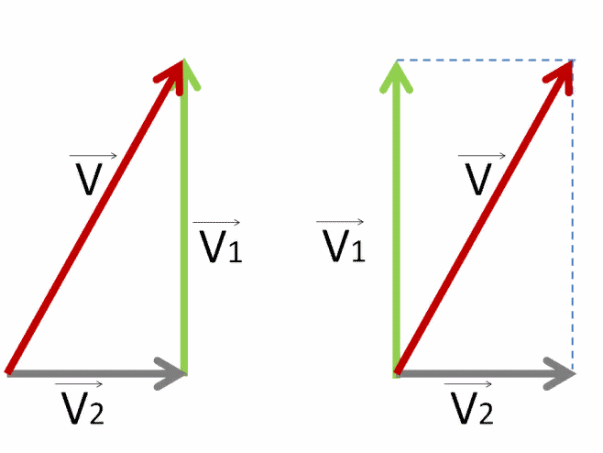
Лайнер плывёт, но сносится течением реки.

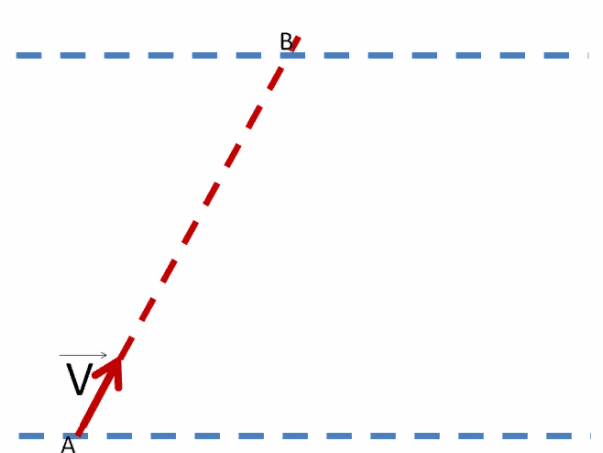
Однако лайнер постоянно стремится переплыть реку со скоростью V⃗₁. Именно с этой скоростью лайнер перемещается к противоположному берегу.

Поэтому в данной задаче нам нужна только скорость лайнера V⃗₁ и ширина реки 370 м.

Чтобы найти время, нужное лайнеру , чтобы переплыть реку, необходимо всё расстояние в 370 м разделить на скорость лайнера V⃗₁.

Получим:

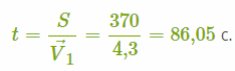
Итак, время, нужное лайнеру , чтобы переплыть реку, составило 86,05c.

Закон сложения скоростей — что это такое

В классической механике применяют термин, который звучит, как абсолютная скорость точки. Данная величина является суммой двух векторов: относительная и переносная скорости точки. В подобном равенстве выражена теорема сложения скоростей. Общепринятым положением является равенство скорости движения какого-либо объекта в рамках неподвижной системы отсчета и векторной суммы скорости аналогичного физического тела в условиях относительно подвижной системы отсчета. Данными координатами определяется непосредственное нахождение тела.

Классический вид, формула расчета

Релятивистским законом сложения скоростей являются соотношения, справедливые для частицы, перемещающейся параллельно относительной скорости систем отсчета:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(К) и (K^{,})

Соотношение теории имеет следующий вид:

(u_{x}=frac{u_{x}^{,}+upsilon }{1+frac{upsilon }{c^{2}}u^{,}_{x}})

(u_{y}=0)

(u_{z}=0)

В случае, когда u<<с, наблюдают переход релятивистских формул в формулы, характерные для классической механики:

(u_{x}=u^{,}_{x}+upsilon)

(u_{y}=0)

(u_{z}=0)

Преобразование координат и времени

Закон сложения скоростей вытекает из физических процессов. Представленное выше соотношение получено в результате преобразований координат и времени. Можно представить частицу, которая в определенное время (t^{,}) зафиксирована в точке с координатами: (x^{,}), (y^{,}), (z^{,}).

Спустя какой-то небольшой промежуток времени (Delta t^{,}) частица переместилась в точку:

(x^{,}+Delta x^{,})

(y^{,}+Delta y^{,})

(z^{,}+Delta z^{,})

В системе отсчета (K^{,}).

Таким образом, при движении частицы происходят два события. Можно записать следующую формулу:

(Delta x^{,}=Delta v^{,}_{x}Delta t^{,})

где ( Delta v^{,}_{x}) представляет собой х компоненту скорости частицы в системе (K^{,}.)

Такие же равенства можно вычислить относительно других компонент. Аналогично координатам преобразуются разности координат и промежутки времени (Delta x), (Delta y), (Delta z). (Delta t).

Уравнения будут иметь следующий вид:

(Delta x=Delta x^{,}+VDelta t^{,})

(Delta y=Delta y^{,})

(Delta z=Delta z^{,})

(Delta t=Delta t^{,})

Исходя из составленных формул можно сделать вывод о том, что компоненты скорости той же частицы в системе (К) будут записаны следующим образом:

(upsilon _{x}=frac{Delta x}{Delta t}=frac{left(Delta x^{,}+VDelta t^{,} right)}{Delta t}=upsilon _{x}^{,} +V)

(upsilon _{y}=upsilon _{y}^{,})

(upsilon _{z}=upsilon _{z}^{,})

Уравнение представляет собой закон сложения скоростей. Данную закономерность можно привести в векторный вид:

(vec{upsilon }=vec{upsilon ^{,}}+V)

Координаты в системе (К) и системе (K^{,}) будут параллельны.

Алгоритм решения задач

Существуют правила, которые являются основой механической физики. Исходя из данных соотношений, можно рассмотреть примеры сложения скоростей. Простейшими объектами для объяснения физических законов являются, к примеру, человек и любой перемещающийся в пространстве объект, с которым он прямо или косвенно взаимодействует.

Пример

Можно представить, что человек совершает прямолинейное движение вдоль коридора пассажирского поезда со скоростью пять километров в час. При этом равномерная скорость состава составляет 100 километров в час. Скорость человека, относительно пространства, которое его окружает, будет равна 105 километрам в час. Следует учитывать одинаковое направление перемещения человека и поезда.

В случае, когда направления движения человека и транспорта противоположны, данный принцип также справедлив. Тогда человек будет двигаться относительно окружающего пространства со скоростью 95 километров в час.

При рассмотрении объектов, скорости которых равны, можно сделать вывод, что относительно друг друга они неподвижны. Во время вращения скорость рассматриваемого тела представляет собой совокупность скоростей перемещения тела относительно движущейся поверхности другого объекта.

Решение задач на сложение скоростей выполняется в несколько этапов:

1. Следует начать с выбора тела отсчета, которое связано с неподвижной системой координат.
2. Далее необходимо определить тело отсчета, которое совершает движение по отношению к первому телу, и связать его с подвижной системой координат.
3. Изучение движения тела в двух координатных системах.
4. Запись закона сложения скоростей, относительно конкретных условий задачи.

Задача 1

На примере рассмотрено равномерное движение двух поездов друг за другом. Первый поезд перемещается со скоростью 80 км/ч, а второй — 60 км/ч. Требуется рассчитать, какова скорость второго поезда относительно первого.

Решение

Следует обозначить скорость первого транспортного средства по отношению к земле с помощью (vec{v_{1}}.)

Тогда скорость  второго поезда составит (vec{v_{2}}.)

Исходя из закона сложения скоростей:

(vec{v_{2}}=vec{v_{2}^{‘}}+vec{v_{1}})

где (vec{v_{2}^{‘}}) является искомой скоростью второго поезда по отношению к первому.

Таким образом:

(vec{v_{2}^{‘}}=vec{v_{2}}-vec{v_{1}})

Такой метод сложения скоростей наглядно представлен на рисунке. Схематично скорость второго поезда по отношению к первому направлена противоположно направлению перемещения поездов, и можно наблюдать удаление второго поезда от первого. Проекция скорости (vec{v_{2}^{‘}}) на ось ОХ будет записана таким образом:

(v_{2}^{‘}=v_{2}-v_{1}=-20)

Ответ: скорость второго поезда относительно первого составит -20 км/ч

Задача 2

Река течет со скоростью (v = 1,5) м/с. Требуется определить модуль скорости (v_{1}) по отношению к воде. Необходимо учитывать, что в случае движения катера перпендикулярно относительно берега, его скорость составляет (v_{2}=2) м/с.

Решение

Исходя из закона сложения скоростей:

(vec{v_{2}}=vec{v_{2}}-vec{v})

Формула для расчета скорости катера относительно реки:

(vec{v_{1}}=vec{v_{1}}+vec{v})

Векторное сложение скоростей представлено на рисунке. На схеме получаем треугольник скоростей с прямым углом, поэтому:

(vec{v_{1}}=2,5)

Ответ: модуль скорости (v_{1}) по отношению к воде составляет (2,5) м/с.

Задача 3

Скорость движения самолета относительно воздуха составляет 300 км/ч. Объект движется в северном направлении. При возникновении северо-западного ветра, скорость которого 100 км/ч по отношению к земле, самолет должен сохранить исходное направление. Требуется рассчитать угол, под которым летчик удерживает направление самолета для продолжения пути на север, а также скорость самолета относительно земли.

Решение

Необходимо связать неподвижную систему отсчета с землей, а подвижную — с воздухом. Скорость самолета по отношению к земле можно рассчитать, как сумму скорости самолета относительно воздуха и скорость ветра относительно земли. В таком случае, исходя из закона сложения скоростей:

(vec{v_{2}}= vec{v_{2}^{‘}}+vec{v})

Рисунок демонстрирует направление этих скоростей. Направление скоростей выполнено таким образом, чтобы проекции скорости самолёта относительно ветра и скорости ветра на оси ОХ равнялись по модулю и были направлены противоположно:

(vec{v_{2x}^{‘}}=-vec{v_{x}})

Таким образом:

(vec{v_{2}^{‘}}cos alpha =vec{v}cos 45^{0})

Если рассматривать проекцию на ось ОУ, то уравнение примет такой вид:

(vec{v_{2y}}=vec{v_{2y}^{‘}}+vec{v_{y}})

В таком случае, искомая скорость самолета составит:

(vec{v_{2y}}=vec{v_{2}^{‘}}sin alpha -vec{v}sin 45^{0})

Данное равенство позволит определить угол α:

(cos alpha =frac{v}{v^{‘}_{2}}cos 45^{0})

Подставив числовые характеристики, получим:

(cos alpha =frac{100}{300}0,707=0,236)

Таким образом:

(alpha =76^{0})

Найти (sin alpha) можно таким образом:

(sin alpha =sqrt{1-left(frac{v}{v^{‘}_{2}} cos 45^{0}right)^{2}})

Скорость самолета относительно земли составит:

(v_{2y}=v^{‘}_{2}sqrt{1-left(frac{v}{v^{‘}_{2}} cos 45^{0}right)^{2}}-vsin 45^{0}approx 220)

Ответ: угол, под которым летчик удерживает направление самолета для продолжения пути на север, равен (76^{0}); скорость самолета относительно земли примерно равна 220 км/ч.