Как определить направление вектора напряженности электрического поля
Содержание
- Характеристика электрического поля
- Силовые линии
- Что называется напряженностью электрического поля
Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы рассматриваем электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.
Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q. Поэтому отношение F/Q не зависит от Q и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
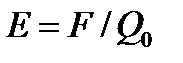
Напряженность поля точечного заряда в вакууме
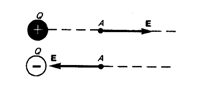
Единица напряженности электростатического поля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — единица потенциала электростатического поля. Графически электростатическое поле изображают с помощьюлиний напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис.).

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой: число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль n которой образует угол a с вектором Е, равно Е dS cosa = EndS, где Еп—проекция вектора Е на нормаль n к площадке dS (рис.).
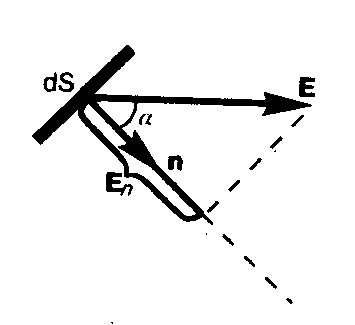
Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
К кулоновским силам применим принцип независимости действия сил, т. е. результирующая сила F, действующая со стороны поля на пробный заряд Q, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Qi: 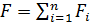
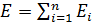
Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке 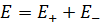
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 — 

Разделы: Физика
Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.
- формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
- научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
- между зарядами нигде не прерываются.
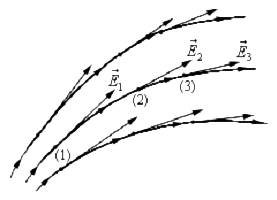
Рис.1
Силовые линии положительного заряда:
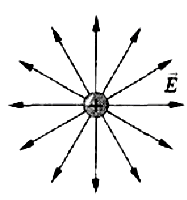
Рис.2
Силовые линии отрицательного заряда:
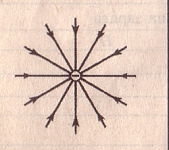
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
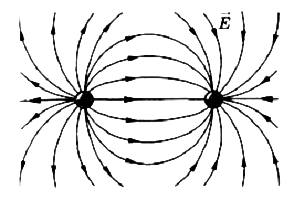
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
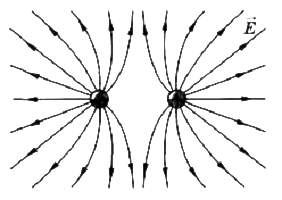
Рис.5
Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения 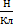

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.
В системе СИ 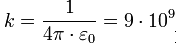
где ε – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
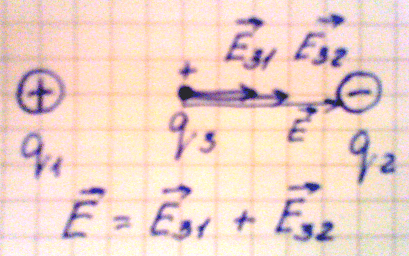
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a) 2 – kq2/a 2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
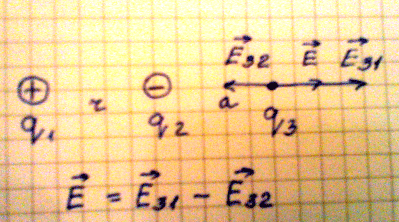
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
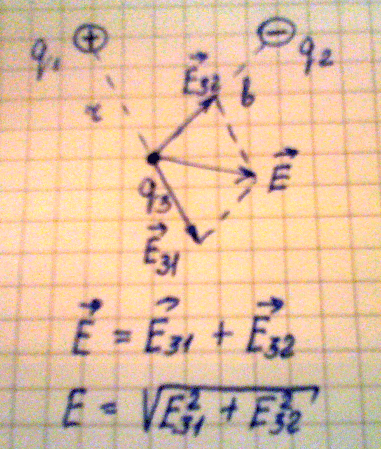
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Два заряда q1 = +3·10 -7 Кл и q2 = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E → = ∑ i = 1 n E → i .
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ = d q d V , где ρ — объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .
В системе СГС напряженность поля точечного заряда в вакууме:
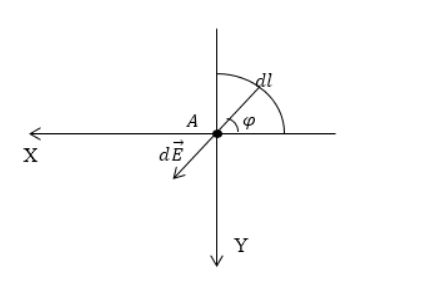
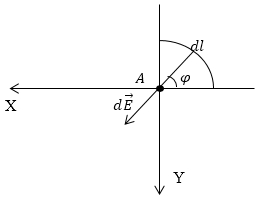
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.
Решение
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:
d E → = d q R 3 R → R .
Проекция вектора d E → на ось О х составит:
d E x = d E cos φ = d q cos φ R 2 .
Произведем выражение d q через линейную плотность заряда τ :
d q = τ d l = τ · 2 πRdR .
Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :
d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
где 2 π d R = d φ .
Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
по d φ с изменением угла 0 ≤ φ ≤ 2 π .
E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .
Перейдем к проекции вектора напряженности на О у :
d E y = d E sin φ = τ R sin φ d φ .
Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :
E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .
Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:
E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .
Ответ: E = τ R 2 .
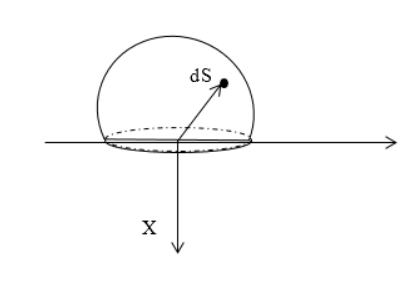
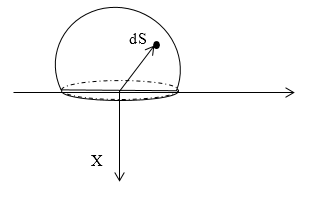
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .
Решение
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:
d S = R 2 sin θ d θ d φ ,
при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .
Элементарная напряженность поля точечного заряда в системе С И :
d E → = d q 4 π ε 0 R 3 R → R .
Необходимо спроецировать вектор напряженности на О х :
d E x = d q cos θ 4 π ε 0 R 2 .
Произведем выражение заряда через поверхностную плотность заряда:
Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:
E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .
Отсюда следует, что E = E x .
Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В соответствии с теорией близкодействия, взаимодействия между заряженными телами, которые удалены друг от друга, осуществляется посредством полей (электромагнитных), создаваемых этими телами в окружающем их пространстве. Если поля создаются неподвижными частицами (телами), то поле является электростатическим. Если поле не изменяется во времени, то его называют стационарным. Электростатическое поле является стационарным. Это поле — частный случай электромагнитного поля. Силовой характеристикой электрического поля служит вектор напряженности, который можно определить как:
где $overrightarrow{F}$- сила, действующая со стороны поля на неподвижный заряд q, который называют иногда «пробным». При этом необходимо, чтобы «пробный» заряд был мал, чтобы не искажал поле, напряженность которого с его помощью измеряют. Из уравнения (1) видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный «пробный заряд».
Напряженность электростатического поля не зависит от времени. Если напряженность во всех точках поля одинакова, то поле называют однородным. В противном случае поле неоднородно.
Силовые линии
Для графического изображения электростатических полей используют понятие силовых линий.
Определение
Силовыми линиями или линиями напряженности поля, называются линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Силовые линии электростатического поля являются разомкнутыми. Они начинаются на положительных зарядах и заканчиваются на отрицательных. Иногда они могут уходить в бесконечность или приходить из бесконечности. Силовые линии поля не пересекаются.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
[overrightarrow{E}=sumlimits^n_{i=1}{{overrightarrow{E}}_i(2)}.]
Результирующий вектор напряженности поля может быть найден как векторная сумма напряженностей составляющих его «отдельных» полей. Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
[overrightarrow{E}=int{doverrightarrow{E}} left(3right).]
В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($tau =frac{dq }{dl}$ -линейная плотность распределения заряда), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $sigma=frac{dq }{dS}$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $rho =frac{dq }{dV}$, где $rho $ — объемная плотность распределения заряда.
Напряженность поля
«Вектор напряженности электрического поля» 👇
Напряжённость поля в диэлектрике равна векторной сумме напряженностей полей, которые создают свободные заряды ($overrightarrow{E_0}$) и связанные заряды ($overrightarrow{E_p}$):
[overrightarrow{E}=overrightarrow{E_0}+overrightarrow{E_p}left(4right).]
Очень часто в примерах мы сталкиваемся с тем, что диэлектрик является изотропным. В таком случае, напряжённость поля может быть записана как:
[overrightarrow{E}=frac{overrightarrow{E_0}}{varepsilon } left(5right),]
где $varepsilon $- относительная диэлектрическая проницаемость среды в рассматриваемой точке поля. Таким образом, из (5) очевидно, что однородном в изотропном диэлектрике напряженность электрического поля в $varepsilon $ раз меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равна:
[overrightarrow{E}=frac{1}{4pi {varepsilon }_0}sumlimits^n_{i=1}{frac{q_i}{varepsilon r^3_i}}overrightarrow{r_i} left(6right).]
В системе СГС напряженность поля точечного заряда в вакууме равна:
[overrightarrow{E}=frac{qoverrightarrow{r}}{r^3}left(7right).]
Пример 1
Задание: Заряд равномерно распределен по четверти окружности радиуса R с линейной плотностью $tau $. Найти напряженность поля в точке (А), которая была бы центром окружности.
Решение:
Рис. 1
Выделим на заряженной части окружности элементарный участок ($dl$), который будет создавать элемент поля в точке А, для него запишем выражение для напряженности (будем использовать систему СГС), в таком случае выражение для $doverrightarrow{E}$ имеет вид:
[doverrightarrow{E}=frac{dq}{R^3}frac{overrightarrow{R}}{R} left(1.1right).]
Проекция вектора $doverrightarrow{E}$ на ось OX имеет вид:
[{dE}_x=dEcosvarphi =frac{dqcosvarphi }{R^2}left(1.2right).]
Выразим dq через линейную плотность заряда $tau $:
[dq=tau dl=tau cdot 2pi RdR left(1.3right).]
Используя (1.3) преобразуем (1.2), получим:
[{dE}_x=frac{2pi Rtau dRcosvarphi }{R^2}=frac{2pi tau dRcosvarphi }{R}=frac{tau cosvarphi dvarphi }{R} left(1.4right),]
где $2pi dR=dvarphi $.
Найдем полную проекцию $E_x$, интегрированием выражения (1.4) по $dvarphi $, где угол изменяется $0le varphi le 2pi $.
[E_x=intlimits^{2pi }_0{frac{tau cosvarphi d varphi }{R}}=frac{tau }{R}intlimits^{2 pi}_0{cosvarphi d varphi=}frac{tau}{R}left({left.sinvarphi right|}^{2pi }_0right)=frac{tau }{R} left(1.5right).]
Займемся проекцией вектора напряженности на ос OY, по аналогии без особых пояснений запишем:
[{dE}_y=dEsinvarphi =frac{tau }{R}sinvarphi d varphi left(1.6right).]
Интегрируем выражение (1.6), угол изменяется $frac{pi }{2}le varphi le 0$, получаем:
[E_y=intlimits^0_{frac{pi }{2}}{frac{tau }{R}sinvarphi dvarphi =frac{tau }{R}intlimits^0_{frac{pi }{2}}{sinvarphi dvarphi =- frac{tau }{R}} }{left.cosvarphi right|}^0_{frac{pi }{2}}=- frac{tau }{R} left(1.7right).]
Найдем модуль вектора напряженности в точке А, используя теорему Пифагора:
[E=sqrt{{E_x}^2+{E_y}^2}=sqrt{{left(frac{tau }{R}right)}^2+{left(-frac{tau }{R}right)}^2}=frac{tau }{R}sqrt{2}]
Ответ: Напряженность поля в точке (А) равна $E=frac{tau }{R}sqrt{2}.$
Пример 2
Задание: Найдите напряженность электростатического поля равномерно заряженной полусферы, радиус которой равен R. Поверхностная плотность заряда равна $sigma$.
Решение:
Рис. 2
Выделим на поверхности заряженной сферы элементарный заряд $dq$, который расположен на элементе площади $dS.$ В сферических координатах $dS$ равен:
[dS=R^2sintheta dtheta dvarphi left(2.1right),]
где $0le varphi le 2pi , 0le theta le frac{pi }{2}.$
Запишем выражение для элементарной напряженности поля точечного заряда в системе СИ:
[doverrightarrow{E}=frac{dq}{{4pi {varepsilon }_0R}^3}frac{overrightarrow{R}}{R} left(2.2right).]
Проектируем вектор напряженности на ось OX, получим:
[{dE}_x=frac{dqcostheta }{4 pi varepsilon_0R^2}left(2.3right).]
Элементарный заряд выразим через поверхностную плотность заряда, получим:
[dq=sigma dS left(2.4right).]
Подставляем (2.4) в (2.3), используем (2.1) интегрируем, получаем:
[E_x=frac{sigma R^2}{4pi {varepsilon }_0R^2}intlimits^{2pi }_0{dvarphi intlimits^{frac{pi }{2}}_0{costheta }}sintheta dtheta =frac{sigma}{4pi {varepsilon }_0}left(2pi cdot frac{1}{2}right)=frac{sigma}{4{varepsilon }_0}.]
Легко получить, что $E_Y=0.$
Следовательно, $E=E_x.$
Ответ: Напряженность поля полусферы заряженной по поверхности в ее центре равна $E=frac{sigma}{4{varepsilon }_0}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E → = ∑ i = 1 n E → i .
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ = d q d V , где ρ — объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .
В системе СГС напряженность поля точечного заряда в вакууме:
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.
Решение
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:
d E → = d q R 3 R → R .
Проекция вектора d E → на ось О х составит:
d E x = d E cos φ = d q cos φ R 2 .
Произведем выражение d q через линейную плотность заряда τ :
d q = τ d l = τ · 2 πRdR .
Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :
d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
где 2 π d R = d φ .
Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
по d φ с изменением угла 0 ≤ φ ≤ 2 π .
E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .
Перейдем к проекции вектора напряженности на О у :
d E y = d E sin φ = τ R sin φ d φ .
Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :
E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .
Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:
E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .
Ответ: E = τ R 2 .
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .
Решение
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:
d S = R 2 sin θ d θ d φ ,
при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .
Элементарная напряженность поля точечного заряда в системе С И :
d E → = d q 4 π ε 0 R 3 R → R .
Необходимо спроецировать вектор напряженности на О х :
d E x = d q cos θ 4 π ε 0 R 2 .
Произведем выражение заряда через поверхностную плотность заряда:
Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:
E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .
Отсюда следует, что E = E x .
Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .
Одной из основных задач электростатики является оценка параметров поля при заданном, стационарном, распределении зарядов в пространстве. Один из способов решения подобных задач основан на принципе суперпозиции. Суть его в следующем.
Если поле создается несколькими точечными зарядами, то на пробный заряд q действует со стороны заряда qk такая сила, как если бы других зарядов не было. Результирующая сила определится выражением:
Т.к. 

 |
(1.4.1) |
Это соотношение выражает принцип наложения или суперпозиции электрических полей и представляет важное свойство электрического поля. Напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из них в отдельности.
Рассмотрим применение принципа суперпозиции в случае поля, созданного электрической системой из двух зарядов с расстоянием между зарядами, равными l (рис. 1.2).
Поля, создаваемые различными зарядами, не влияют друг на друга, поэтому вектор 


В данном случае
 |
(1.4.2) |
Рассмотрим другой пример. Найдем напряженность электростатического поля Е, создаваемую двумя положительными зарядами q 1 и q 2 в точке А, находящейся на расстоянии r 1 от первого и r 2 от второго заря-дов (рис. 1.3).
Воспользуемся теоремой косинусов:
 |
(1.4.3) |
Если поле создается не точечными зарядами, то используют обычный в таких случаях прием. Тело разбивают на бесконечно малые элементы и определяют напряженность поля создаваемого каждым элементом, затем интегрируют по всему телу:
 |
(1.4.4) |
Если же поле создано сложными по форме заряженными телами и неравномерно заряженными, то используя принцип суперпозиции, трудно найти результирующее поле.
формуле (1.4.4) мы видим, что 
 |
(1.4.5) |
В качестве примеров можно рассмотреть линейное распределение зарядов или распределение заряда по окружности.
Определим напряженность электрического поля в точке А (рис. 1.4) на расстоянии х от бесконечно длинного, линейного, равномерно распределенного заряда. Пусть λ – заряд, приходящийся на единицу длины.
Считаем, что х – мало по сравнению с длиной проводника. Выберем систему координат так, чтобы ось y совпадала с проводником. Элемент длины dy, несет заряд 
 |
(1.4.6) |
Вектор 




Тогда 



 |
(1.4.7) |
Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.
Этот результат, полученный для бесконечно длинного линейного заряда, с хорошей точностью справедлив и для линейного заряда конечной длины при условии, что х – мало по сравнению с расстоянием от точки А до концов проводника.
Задание: по тонкому кольцу радиуса R равномерно распределен заряд q. Определить Е в точке А (рис. 1.5).
Разделы: Физика
Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.
- формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
- научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
- между зарядами нигде не прерываются.

Рис.1
Силовые линии положительного заряда:

Рис.2
Силовые линии отрицательного заряда:

Рис.3
Силовые линии одноименных взаимодействующих зарядов:

Рис.4
Силовые линии разноименных взаимодействующих зарядов:

Рис.5
Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения 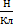

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.
В системе СИ 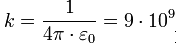
где ε 0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
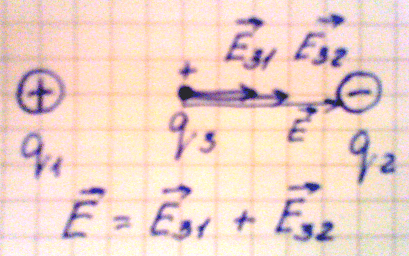
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a) 2 – kq2/a 2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
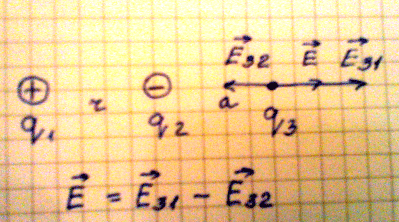
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
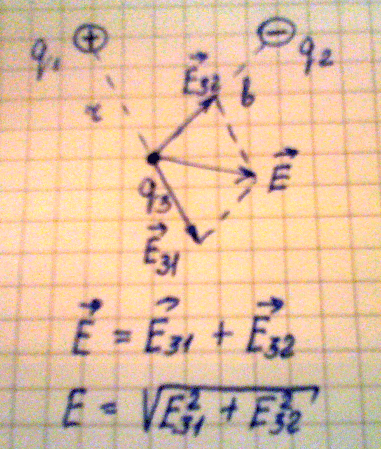
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Два заряда q1 = +3·10 -7 Кл и q2 = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.
Содержание:
- Определение и формула напряженности электрического поля
- Принцип суперпозиции напряженностей электрических полей
- Напряженность поля в диэлектрике
- Напряженность поля точечного заряда
- Связь напряженности и потенциала
- Единицы измерения напряженности электрического поля
- Примеры решения задач
Определение и формула напряженности электрического поля
Определение
Вектор напряженности $bar{E}$ – это силовая характеристика электрического поля. В некоторой точке поля, напряженность равна
силе, с которой поле действует на единичный положительный заряд, размещенный в указанной точке, при этом направление силы и напряженности
совпадают. Математическое определение напряженности записывается так:
$$bar{E}=frac{bar{F}}{q}$$
где $bar{F}$ – сила, с которой электрическое поле действует на
неподвижный, «пробный», точечный заряд q, который размещают в рассматриваемой точке поля. При этом считают, что «пробный» заряд
мал на столько, что не искажает исследуемого поля.
Если поле является электростатическим, то его напряженность от времени не зависит.
Если электрическое поле является однородным, то его напряженность во всех точках поля одинакова.
Графически электрические поля можно изображать при помощи силовых линий. Силовыми линиями (линиями напряженности) называют
линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке поля.
Принцип суперпозиции напряженностей электрических полей
Если поле создано несколькими электрическими полями, то напряженность результирующего поля равна векторной сумме напряженностей отдельных полей:
$$bar{E}=sum_{i=1}^{n} bar{E}_{i}(2)$$
Допустим, что поле создается системой точечных зарядов и их распределение непрерывно, тогда результирующая напряженность находится как:
$$bar{E}=int d bar{E}(3)$$
интегрирование в выражении (3) проводят по всей области распределения заряда.
Напряженность поля в диэлектрике
Напряженность поля $bar{E}$ в диэлектрике равна векторной сумме
напряженностей полей, создаваемых свободными зарядами $bar{E}_0$ и
связанными (поляризационными зарядами) $bar{E}_p$:
$$bar{E}=bar{E}_{0}+bar{E}_{p}(4)$$
В том случае, если вещество, которое окружает свободные заряды однородный и изотропный диэлектрик, то напряженность
$bar{E}$ равна:
$$bar{E}=frac{bar{E}_{0}}{varepsilon}(5)$$
где $varepsilon$ – относительная диэлектрическая проницаемость вещества в исследуемой точке
поля. Выражение (5) обозначает то, что при заданном распределении зарядов напряженность электростатического поля в однородном изотропном
диэлектрике меньше, чем в вакууме в $varepsilon$ раз.
Напряженность поля точечного заряда
Напряженность поля точечного заряда q равна:
$$bar{E}=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{3}} bar{r}(6)$$
где $varepsilon_{0}=8,85 cdot 10^{-12}$ Ф/м (система СИ) — электрическая постоянная.
Связь напряженности и потенциала
В общем случае напряженность электрического поля связана с потенциалом как:
$$bar{E}=-operatorname{grad} varphi-frac{partial bar{A}}{partial t}(7)$$
где $varphi$ – скалярный потенциал,
$bar{a}$ – векторный потенциал.
Для стационарных полей выражение (7) трансформируется в формулу:
$$bar{E}=-operatorname{grad} varphi(8)$$
Единицы измерения напряженности электрического поля
Основной единицей измерения напряженности электрического поля в системе СИ является: [E]=В/м(Н/Кл)
Примеры решения задач
Пример
Задание. Каков модуль вектора напряженности электрического поля
$bar{E}$ в точке, которая определена радиус- вектором
$bar{r}_{2}=7 bar{i}+3 bar{j}$ (в метрах), если электрическое поле создает положительный точечный
заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор
$bar{r}_{1}=bar{i}-5 bar{j}$, (в метрах)?
Решение. Модуль напряжения электростатического поля, которое создает точечный заряд, определяется формулой:
$$E=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{2}}(1.1)$$
r- расстояние от заряда, создающего поле до точки в которой ищем поле.
$$bar{r}=bar{r}_{2}-bar{r}_{1}=6 bar{i}-8 bar{j}(1.2)$$
Из формулы (1.2) следует, что модуль $bar{r}$ равен:
$$r=|bar{r}|=sqrt{36+64}=10(mathrm{~m})$$
Подставим в (1.1) исходные данные и полученное расстояние r, имеем:
$$E=9 cdot 10^{9} frac{1}{100}=9 cdot 10^{7}left(frac{B}{m}right)$$
Ответ. $E=9 cdot 10^{7}left(frac{B}{m}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Запишите выражение для напряженности поля в точке, которая определена радиус – вектором
$bar{r}$, если поле создается зарядом, который распределен по объему V с плотностью
$rho=rho(r)$ .
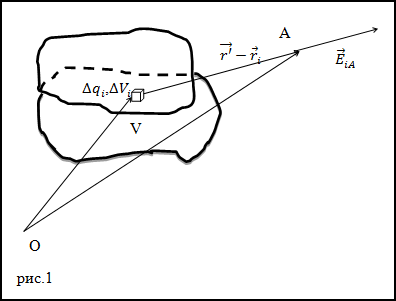
Решение. Сделаем рисунок.
Проведем разбиение объема V на малые области с объемами
$Delta V_{i}$ заряды этих объемов
$Delta q_{i}$, тогда напряженность поля точечного заряда в точке А (рис.1) будет равна:
$$bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.1)$$
Для того чтобы найти поле, которое создает все тело в точке А, используем принцип суперпозиции:
$$bar{E}_{A}=sum_{i=1}^{N} bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.2)$$
где N – число элементарных объемов, на которые разбивается объем V.
Плотность распределения заряда можно выразить как:
$rholeft(bar{r}_{i}right)=frac{Delta q_{i}}{Delta V_{i}}(2.3)$
Из выражения (2.3) получим:
$Delta q_{i}=rholeft(bar{r}_{i}right) Delta V_{i}(2.4)$
Подставим выражение для элементарного заряда в формулу (2.2), имеем:
$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{rholeft(bar{r}_{i}right) Delta V_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.5)$$
Так ка распределение зарядов задано непрерывное, то если устремить
$Delta V_i$ к нулю, то можно перейти от суммирования к интегрированию, тогда:
$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$$
Ответ. $bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$
Читать дальше: Формула пути.
Методика
решения задач на нахождение напряжённости
результирующего поля аналогична методике
нахождения результирующей силы,
действующей на точечный заряд со стороны
других точечных зарядов (см. раздел
1.1), только вместо закона Кулона
используется формула напряженности
точечного заряда (2.2).

Задача
2.1. Два
точечных заряда q1
и q2
находятся на расстоянии d
друг от друга. Найти напряжённость в
точках А, В, С и D
(рис. 13). Считаем расстояния от зарядов
q1
и q2
до заданных точек известными и во всех
случаях обозначаем r1
и r2
соответственно.
Р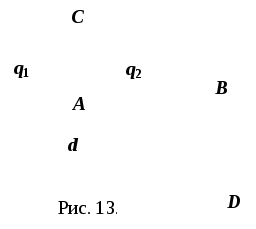
Сделаем рисунок для каждого случая
отдельно. Так как заряды оба отрицательные,
то векторы напряжённостей
и
направлены в каждом случае к зарядамq1
и q2
вдоль линии, соединяющей заряд и заданную
точку, и берут начало в заданной точке.
Направление
результирующего вектора
определяетсяпо
принципу суперпозиции
путём векторного сложения. Поэтому
векторная запись для всех случаев
одинакова:
.
Модуль
(длина) каждого из векторов рассчитывается
по формуле напряженности точечного
заряда (2.2). Модуль результирующего
вектора определяется из геометрических
построений.
-
В
точке А (рис. 14, а) векторы
и
направлены в противоположные стороны,
поэтому модуль результирующего вектораопределяется как разность модулей
векторови
и направлен в сторону большего вектора:
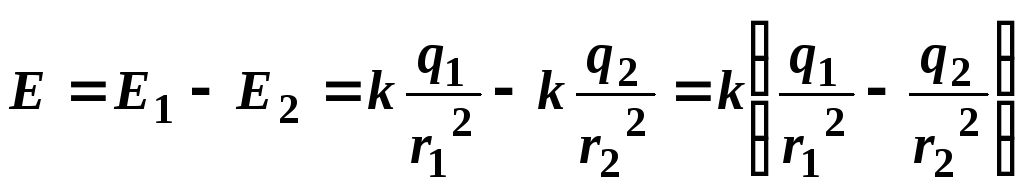
-
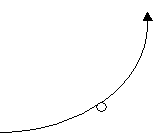
В
точке В (рис. 14, б) векторы
и
направлены в одну сторону, поэтому
модуль результирующего вектораопределяется
как сумма модулей векторови
и направлен в эту же сторону:
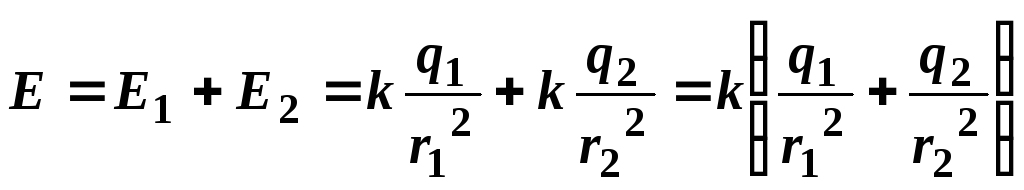
-
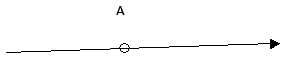
В
точке С (рис. 14, в) векторы
и
взаимно перпендикулярны, поэтому модуль
результирующего вектораявляется гипотенузой прямоугольного
треугольника и определяется по теореме
Пифагора:
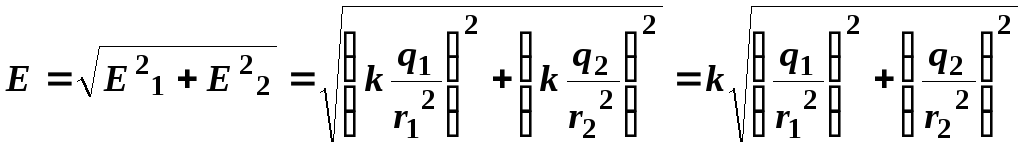
-
В
точке D
(рис. 14, г) векторы
и
образуют треугольник, поэтому модуль
результирующего вектораопределяется
по теореме косинусов:
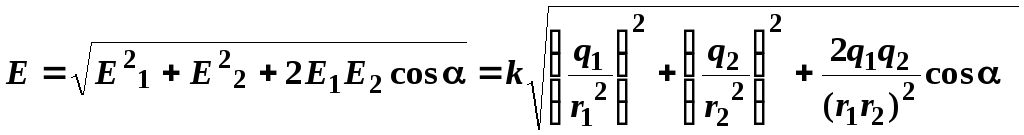
Если
угол α
неизвестен, то его определяют, используя
теорему косинусов для треугольника со
сторонами r1,
r2,
d:
.
Задача
2.2. Поле
создано тремя одинаковыми точечными
зарядами q,
расположенными в вершинах равностороннего
треугольника со стороной а.
Вычислить напряжённость электростатического
поля в точке, находящейся на пересечении
высот этого треугольника.
Решение.
Так как напряжённость электростатического
поля
– величина
векторная, то необходимо определить
направление этого вектора и его модуль
(длину).
Направление
вектора напряжённости результирующего
поля определяем с помощью принципа
суперпозиции:
,
где
,
и
— напряжённость электростатического
поля, созданного каждым зарядом в
отдельности.
-
С
начала
строим векторы,
и
,
берущиеначало
в заданной точке. Так как все заряды
одинаковые, а заданная точка равноудалена
от них, то длины этих векторов будут
равны. Поскольку знак зарядов
отрицательный, то векторы
,
и
будут направлены к зарядам (рис. 15).
-
Складываем
геометрически векторы
и
.
Результирующий векторбудет лежать на той же прямой, что и
вектор.
-
Находим
длину вектора
по теореме косинусов:
,
где
α
– угол между векторами
и
.
С
учётом того, что Е1
= Е2,
α = 120º, cos 120º
= – 0,5, получим:
.
-
Складываем
геометрически векторы
и
.Так
как эти векторы равны по длине и
противоположны по направлению, то их
векторная сумма равна нулю:
.
Методика
расчета не меняется, если образующие
систему заряды имеют другие знаки и
расположения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


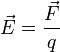
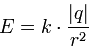
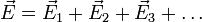
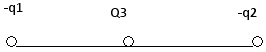



 точке С (рис. 14, в) векторы
точке С (рис. 14, в) векторы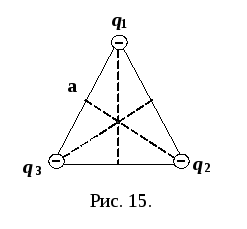 начала
начала