Как найти решение системы уравнений методом подстановки - AvtoShod.ru

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки:

1) из более простого уравнения системы выразить одно неизвестное через другое;

2) подставить полученное выражение в другое уравнение вместо выраженной переменной;

3) найти корень полученного уравнения с одним неизвестным;

4) подставить найденное значение в уравнение, полученное на первом шаге, и найти вторую переменную;

Пример:

решить систему:

x−2y=3,5x+y=4.

1) Выразим из первого уравнения переменную (x):

x−2y=3;x=3+2y.

2) Подставим (3+2y) вместо (x) во второе уравнение:

5⋅x+y=4;5⋅3+2y+y=4.

3) Решим линейное уравнение относительно (y):

5⋅3+2y+y=4;15+10y+y=4;10y+y=4−15;11y=−11:11y=−1.¯

4) Подставим в первое уравнение вместо (y) полученное значение и найдём (x):

x=3+2⋅y;x=3+2⋅−1x=3−2;x=1.¯

5) Ответ:

1;−1

Источник

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Запомните!

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют
«x» и «y»),
которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Важно!

Чтобы выразить неизвестное, нужно выполнить два условия:

перенести неизвестное, которое хотим выразить, в левую часть уравнения;
разделить и левую и правую часть уравнения на нужное число так,
чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4 (*)

(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

Запомните!

При сложения уравнений системы
левая часть первого уравнения полностью складывается
с левой частью второго уравнения,
а правая часть полностью складывается с
правой частью.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+ =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

Важно!

При умножении уравнения на число, на это число умножается каждый член уравнения.

	x + 5y = 7 \| ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+ =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 \|:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4 \|·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+ =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8 \| :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

8 мая 2020 в 16:20

Алина Козлова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Алина Козлова
Профиль
Благодарили: 0

Сообщений: 1

у-2х=-3
х+у=3

0
Спасибо thanks
Ответить

9 мая 2020 в 21:50
Ответ для Алина Козлова

Evgeny Bayron
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Evgeny Bayron
Профиль
Благодарили: 0

Сообщений: 1

y=3-x
3-x-2x=-3
x=2
y-2*2=-3
y=1

0
Спасибо thanks
Ответить

15 мая 2019 в 13:21

Марина Чернявская
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Марина Чернявская
Профиль
Благодарили: 0

Сообщений: 1

Решительно систему уравнений.
4x+3y =22.
-x+7y =10.
a)графическим способом.
б)способом подстановки
в)способом сложения

0
Спасибо thanks
Ответить

15 мая 2019 в 22:31
Ответ для Марина Чернявская

Лёха Чешуйка
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Лёха Чешуйка
Профиль
Благодарили: 0

Сообщений: 2

в): Домножаем первое на 1, второе на 4:
4x+3y=22
-4x+28y=40
Складываем:
4x+(-4x)+3y+28y=22+40
31y=62
y=62/31
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4

0
Спасибо thanks
Ответить

15 мая 2019 в 22:41
Ответ для Марина Чернявская

Лёха Чешуйка
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Лёха Чешуйка
Профиль
Благодарили: 0

Сообщений: 2

б): Выражаем из второго x:
-x=10-7y
x=7y-10
Подставляем x в первое:
4(7y-10)+3y=22
28y-40+3y=22
31y=22+40
31y=62
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4

0
Спасибо thanks
Ответить

20 октября 2015 в 13:24

Елена Тутуликова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Елена Тутуликова
Профиль
Благодарили: 0

Сообщений: 1

Помогите, пожалуйста, решить систему уравнений.{y + sinx = 5; {4y + 2 sinx = 19
Спасибо!

0
Спасибо thanks
Ответить

23 октября 2015 в 21:25
Ответ для Елена Тутуликова

Елизавета Яременко
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Елизавета Яременко
Профиль
Благодарили: 0

Сообщений: 5

Я думаю{y + sinx =5; {4y + 2 sinx =19

0
Спасибо thanks
Ответить

9 июня 2016 в 14:19
Ответ для Елена Тутуликова

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

sinx = 1/2
y = 9/2

0
Спасибо thanks
Ответить

Источник

Алгоритм решения системы линейных уравнений методом подстановки

Из любого уравнения системы выразить одну переменную через другую.
Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
Решить второе уравнение относительно выраженной переменной.
Подставить найденное значение переменной в выражение, полученное на первом шаге.
Найти значение второй переменой.
Записать ответ в виде упорядоченной пары найденных значений переменных.

Например: ${left{ begin{array}{c} 3x+y = 5 \ y-x = 1 end{array} right.}$

Шаг 1

Из второго уравнения выражаем y:

y = x+1

Шаг 2

Подставляем выражение для y в первое уравнение:

3x+(x+1) = 5

Шаг 3 Решаем первое уравнение:

4x = 5-1

x = 1

Шаг 4

Подставляем значение x в выражение для y:

y = 1+1

Шаг 6

Записываем ответ:

(1;2)

В последовательной записи:

$$ {left{ begin{array}{c} 3x+y = 5 \ y-x = 1 end{array} right.} Rightarrow {left{ begin{array}{c} 3x+y = 5 \ y = x+1 end{array} right.} Rightarrow {left{ begin{array}{c} 3x+(x+1) = 5 \ y = x+1 end{array} right.} Rightarrow {left{ begin{array}{c} 4x = 5-1 \ y = x+1 end{array} right.} Rightarrow $$ $$ Rightarrow {left{ begin{array}{c} x = 1 \ y = x+1 end{array} right.} Rightarrow {left{ begin{array}{c} x = 1 \ y = 2end{array} right.} $$

Ответ: (1;2)

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) {left{ begin{array}{c} 5x-4y = 3 \ 2x-3y = 4 end{array} right.} Rightarrow {left{ begin{array}{c} 5x-4y = 3 \ x = frac{3y+4}{2} = 1,5y+2 end{array} right.} Rightarrow {left{ begin{array}{c} 5(1,5y+2)-4y = 3 \ x = 1,5y+2 end{array} right.} Rightarrow $

$ Rightarrow {left{ begin{array}{c} 7,5y+10-4y = 3 \ x=1,5y+2 end{array} right.} Rightarrow {left{ begin{array}{c} 3,5y = -7 \ x = 1,5y+2 end{array} right.} Rightarrow {left{ begin{array}{c} y = -2 \ x = 1,5y+2 end{array} right.} Rightarrow {left{ begin{array}{c} x = -1 \ y = -2end{array} right.} $

Ответ: (-1;-2)

$ б) {left{ begin{array}{c} 4x-3y = 7 \ 3x-4y = 0 end{array} right.} Rightarrow {left{ begin{array}{c} 4x-3y = 7 \ y = frac{3}{4} x end{array} right.} Rightarrow {left{ begin{array}{c} 4x-3cdot frac{3}{4} x = 7 \ y = frac{3}{4} x end{array} right.} Rightarrow {left{ begin{array}{c} (4- frac{9}{4})x = 7 \ y = frac{3}{4} x end{array} right.} Rightarrow $

$Rightarrow {left{ begin{array}{c} x = 7 cdot frac{4}{7} = 4 \ y = frac{3}{4} x = frac{3}{4} cdot 4 = 3 end{array} right.} Rightarrow {left{ begin{array}{c}x = 4 \ y = 3 end{array} right.} $

Ответ: (4;3)

$ в) {left{ begin{array}{c} 5a-4b = 9 \ 2a+3b = -1 end{array} right.} Rightarrow {left{ begin{array}{c} 5a-4b = 9 \ a = frac{-3b-1}{2} = -1,5b-0,5 end{array} right.} Rightarrow {left{ begin{array}{c} 5(-1,5b-0,5)-4b = 9 \ a = -1,5b-0,5 end{array} right.} Rightarrow $

$ Rightarrow {left{ begin{array}{c} -7,5b-2,5-4b = 9 \ a = -1,5b-0,5 end{array} right.} Rightarrow {left{ begin{array}{c}-11,5b = 11,5 \ a = -1,5b-0,5 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -1 end{array} right.} $

Ответ: (1;-1)

$ г) {left{ begin{array}{c} 7a+4b = 5 \ 3a+2b = 1 end{array} right.} Rightarrow {left{ begin{array}{c} 7a+4b = 5 \ b = frac{-3a+1}{2} = -1,5a+0,5 end{array} right.} Rightarrow {left{ begin{array}{c} 7a+4(-1,5a+0,5) = 5 \ b = -1,5a+0,5 end{array} right.} Rightarrow $

$ Rightarrow {left{ begin{array}{c} 7a-6a+2 = 5 \ b = -1,5a+0,5 end{array} right.} Rightarrow {left{ begin{array}{c} a = 3 \ b = -1,5cdot3+0,5 = -4 end{array} right.} $

Ответ: (3;-4)

Пример 2. Найдите решение системы уравнений:

$а) {left{ begin{array}{c} frac{x}{4}-y = 7 | times 4 \ 3x+ frac{y}{2} = 9 | times 2end{array} right.} Rightarrow {left{ begin{array}{c} x-4y = 28 \ 6x+y = 18 end{array} right.} Rightarrow {left{ begin{array}{c} x = 4y+28 = 4(y+7) \ 6 cdot 4(y+7)+y = 18 end{array} right.} Rightarrow $

$Rightarrow {left{ begin{array}{c} x = 4(y+7) \ 24y+168+y = 18 end{array} right.} Rightarrow {left{ begin{array}{c} x = 4(y+7) \ 25y = -150 end{array} right.} Rightarrow {left{ begin{array}{c}x = 4(-6+7) = 4 \ y = -6 end{array} right.}$

Ответ: (4;-6)

$б) {left{ begin{array}{c} frac{x}{2}+ frac{y}{3} = frac{1}{6} |times 6 \ frac{x}{3}+ frac{y}{2} = -frac{1}{6}| times 6 end{array} right.}Rightarrow {left{ begin{array}{c} 3x+2y = 1 \ 2x+3y = -1 end{array} right.} Rightarrow {left{ begin{array}{c} y = frac{-3x+1}{2} = -1,5x+0,5 \ 2x+3(-1,5x+0,5) = -1end{array} right.} Rightarrow$

$ Rightarrow {left{ begin{array}{c} y = -1,5x+0,5 \ 2x-4,5x+1,5 = -1end{array} right.} Rightarrow {left{ begin{array}{c} y = -1,5x+0,5 \ -2,5x = -2,5 end{array} right.} Rightarrow {left{ begin{array}{c} x = 1 \ y = -1 end{array} right.} $

Ответ: (1;-1)

$ в) {left{ begin{array}{c} 3(5x-y)+14 = 5(x+y) \ 2(x-y)+9 = 3(x+2y)-16 end{array} right.} Rightarrow {left{ begin{array}{c} 15x-3y+14 = 5x+5y \ 2x-2y+9 = 3x+6y-16 end{array} right.} Rightarrow $

$ Rightarrow {left{ begin{array}{c} 10x-8y = -14 |:2 \ x+8y = 25 end{array} right.} Rightarrow {left{ begin{array}{c} 5x-4y = -7 \ x = -8y+25 end{array} right.} Rightarrow {left{ begin{array}{c} 5(-8y+25)-4y = -7 \ x = -8y+25 end{array} right.} Rightarrow $

$ Rightarrow {left{ begin{array}{c} -40y+125-4y = -7 \ x = -8y+25 end{array} right.} Rightarrow {left{ begin{array}{c} -44y = -132 \ x = -8y+25 end{array} right.} Rightarrow {left{ begin{array}{c} x = 1 \ y = 3 end{array} right.} $

Ответ: (1;3)

$ г) {left{ begin{array}{c} 5-3(2x+7y) = x+y-52 \ 4+3(7x+2y) = 23x end{array} right.} Rightarrow {left{ begin{array}{c} 5-6x-21y = x+y-52 \ 4+21x+6y = 23x end{array} right.} Rightarrow {left{ begin{array}{c} 7x+22y = 57 \ 2x-6y = 4 |:2 end{array} right.}$

$$ Rightarrow {left{ begin{array}{c} 7x+22y = 57 \ x-3y = 2 end{array} right.} Rightarrow {left{ begin{array}{c} 7x+22y = 57 \ x = 3y+2 end{array} right.} Rightarrow {left{ begin{array}{c} 7(3y+2)+22y = 57 \ x = 3y+2 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} 21y+14+22y = 57 \ x = 3y+2 end{array} right.} Rightarrow {left{ begin{array}{c} 43y = 43 \ x = 3y+2 end{array} right.} Rightarrow {left{ begin{array}{c} x = 5 \ y = 1 end{array} right.}$$

Ответ: (5;1)

Пример 3*. Найдите решение системы уравнений:

$ {left{ begin{array}{c} frac{3}{2x-5y} + frac{8}{x+y} = 5 \ frac{12}{x+y} — frac{1}{2x-5y} = 2 end{array} right.} $

Введём новые переменные: $ {left{ begin{array}{c} a = frac{1}{2x-5y} \ b = frac{1}{x+y} end{array} right.} $

Перепишем систему и найдём решение для новых переменных:

$$ {left{ begin{array}{c} 3a+8b = 5 \ 12b-a = 2 end{array} right.} Rightarrow {left{ begin{array}{c} 3(12b-2)+8b = 5 \ a = 12b-2 end{array} right.} Rightarrow {left{ begin{array}{c} 36b-6+8b = 5 \ a = 12b-2 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} 44b = 11 \ a = 12b-2 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = frac{1}{4} end{array} right.} $$

Получаем:

$$ {left{ begin{array}{c} 2x-5y = frac{1}{a} = 1 \ x+y = frac{1}{b} = 4 end{array} right.} Rightarrow {left{ begin{array}{c} 2x-5(4-x) = 1 \ y = 4-x end{array} right.} Rightarrow {left{ begin{array}{c} 2x-20+5x = 1 \ y = 4-x end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} 7x = 21 \ y = 4-x end{array} right.} Rightarrow {left{ begin{array}{c} x = 3 \ y = 1 end{array} right.} $$

Ответ: (3;1)

Источник

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Правила ввода уравнений

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются.
Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Пример подробного решения (методом подстановки и сложения) >>

Наши игры, головоломки, эмуляторы:

Немного теории.

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left{ begin{array}{l} 3x+y=7 \ -5x+2y=3 end{array} right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left{ begin{array}{l} y = 7—3x \ -5x+2(7-3x)=3 end{array} right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только
одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений,
также считают равносильными.

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при
решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит
только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали
противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left{ begin{array}{l} 2x+3y=-5 \ x-3y=38 end{array} right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений,
получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left{ begin{array}{l} 3x=33 \ x-3y=38 end{array} right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с
переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к
решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит
только одну переменную.

Источник

Рассмотрим тему «Решение систем линейных уравнений методом подстановки».

В учебнике данная теория излагается на странице 203-206.

Алгоритм:
Для решения системы линейных уравнений с двумя переменными методом подстановки поступаем следующим образом:
1) выражаем одну переменную через другую в одном из уравнений системы (х через у или у через х);
2) подставляем полученное выражение в другое уравнение системы и получаем линейное уравнение с одной переменной;
3) решаем полученное линейное уравнение с одной переменной и находим значение этой переменной;
4) найденное значение переменной подставляем в выражение (1) для другой переменной и находим значение этой переменной.

Примеры. Решить методом подстановки систему линейных уравнений.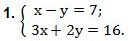
Выразим х через у из 1-го уравнения. Получим: х=7+у. Подставим выражение (7+у) вместо х во 2-ое уравнение системы.

Мы получили уравнение: 3·(7+у)+2у=16. Это уравнение с одной переменной у. Решаем его. Раскроем скобки: 21+3у+2у=16. Собираем слагаемые с переменной у в левой части, а свободные слагаемые — в правой. При переносе слагаемого из одной части равенства в другую меняем знак слагаемого на противоположный.

Получаем: 3у+2у=16-21. Приводим подобные слагаемые в каждой части равенства. 5у=-5. Делим обе части равенства на коэффициент при переменной. у=-5:5; у=-1. Подставляем это значение у в выражение х=7+у и находим х. Получаем: х=7-1; х=6. Пара значений переменных х=6 и у=-1 является решением данной системы.

Записывают: (6; -1). Ответ: (6; -1). Эти рассуждения удобно записывать так, как показано ниже, т.е. системы уравнений — слева друг под другом. Справа — выкладки, необходимые пояснения, проверка решения и пр.