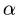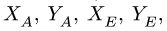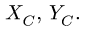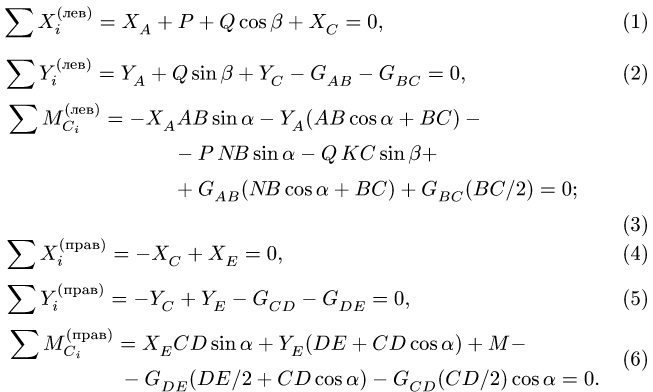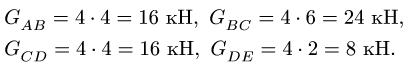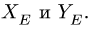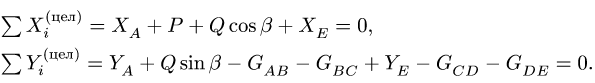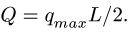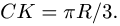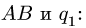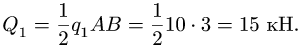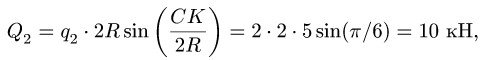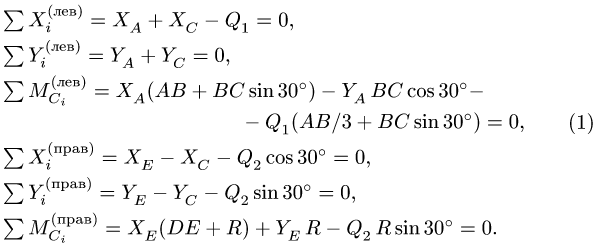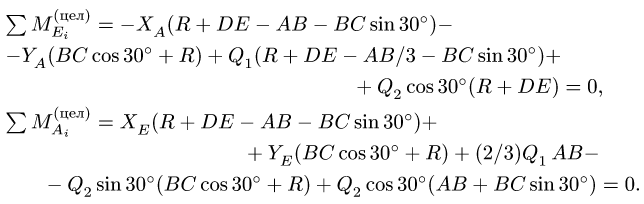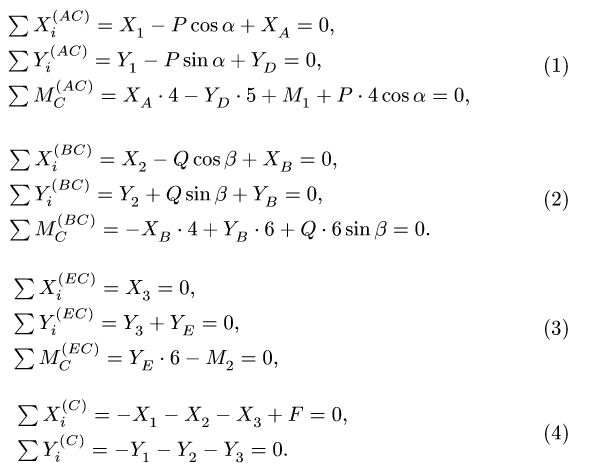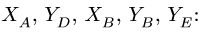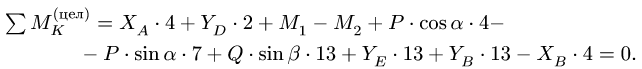Расчет составной конструкции:
Постановка задачи. Плоская рама состоит из двух частей, соединенных одним шарниром. На раму действует момент и силы. Учитывая погонный вес, найти реакции опор.
План решения:
Составная конструкция, состоящая из двух тел, соединенных шарниром содержит четыре неизвестные реакции опор. Так как для одного тела под действием плоской системы сил можно составить только три независимых уравнения равновесия, то для определения реакций необходимо рассматривать равновесие каждой части составной конструкции в отдельности.
1-й способ:
1. Разбиваем систему на два тела по сочленяющему шарниру. В месте разбиения прикладываем реакции отброшенной части. Внешние связи заменяем их реакциями.
2. Для каждого тела, образованного при разбиении, составляем по три уравнения равновесия.
3. Решаем систему шести уравнений. Определяем реакции опор.
4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.
2-й способ:
1. Разбиваем систему на два тела по сочленяющему шарниру. В месте разбиения прикладываем реакции отброшенной части. Внешние связи заменяем их реакциями.
2. Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом.
3. Решаем систему четырех уравнений. Определяем реакции опор.
4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.
Задача №1
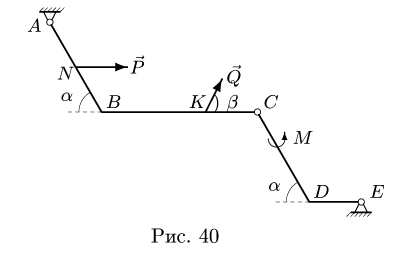
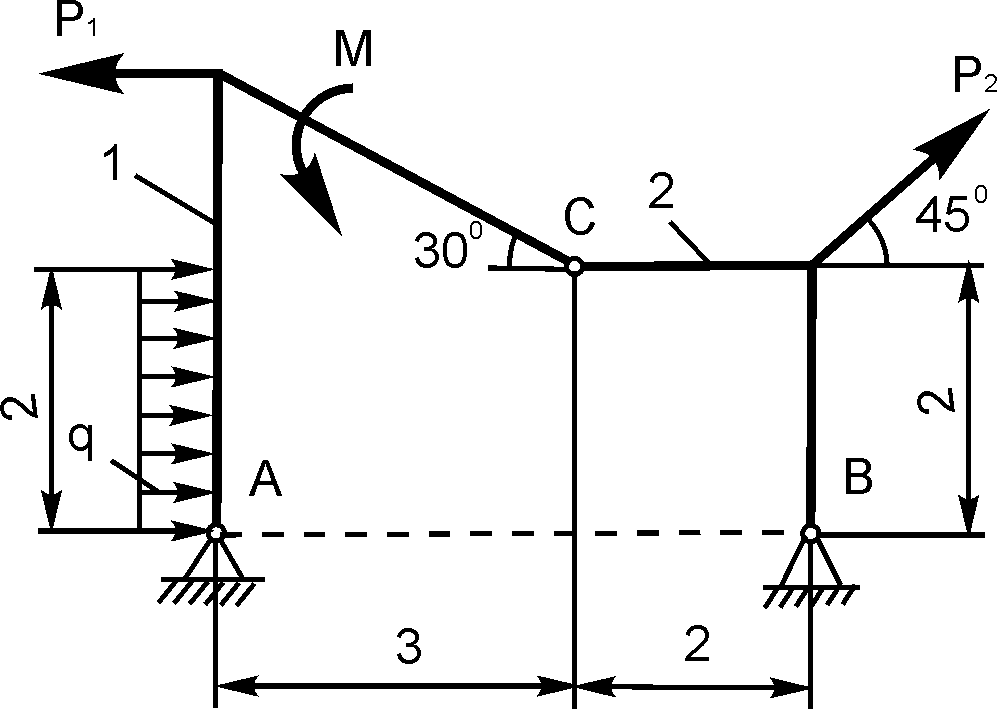
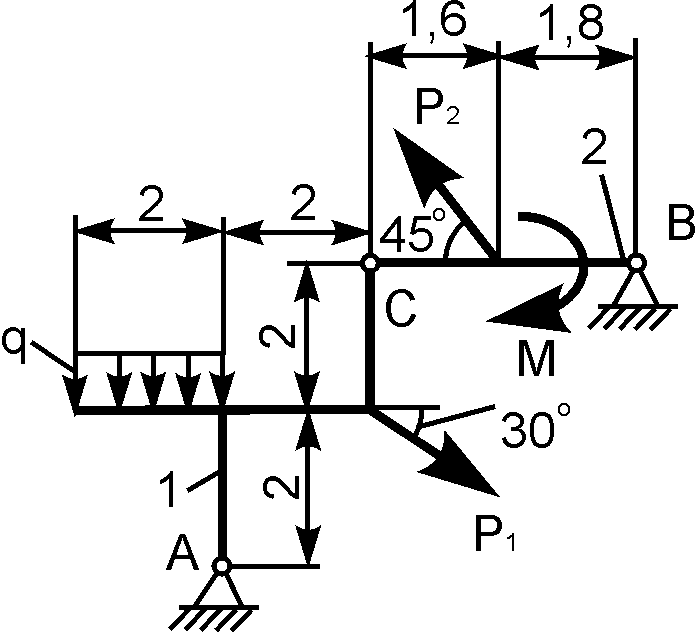
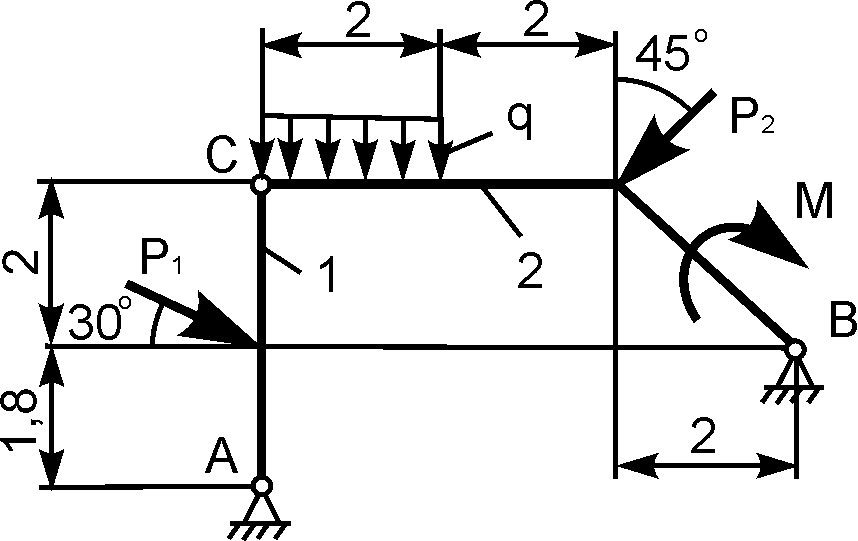
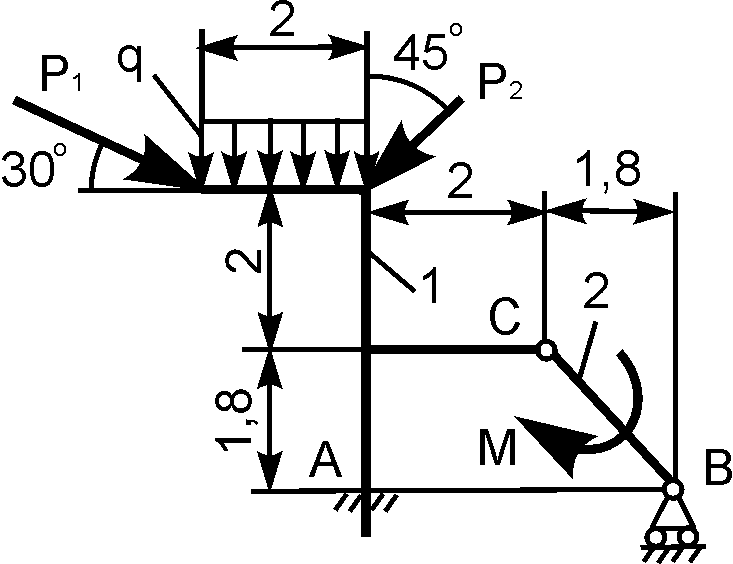
Плоская рама состоит из двух частей, соединенных в точке С шарниром. На раму действует момент М = 100 кНм, горизонтальная сила Р = 20 кН и наклонная сила Q = 10 кН. Учитывая погонный вес р = 4 кН/м, найти реакции опор (рис. 40). Дано:
2.4. Расчет составной конструкции
Решение
1-й способ
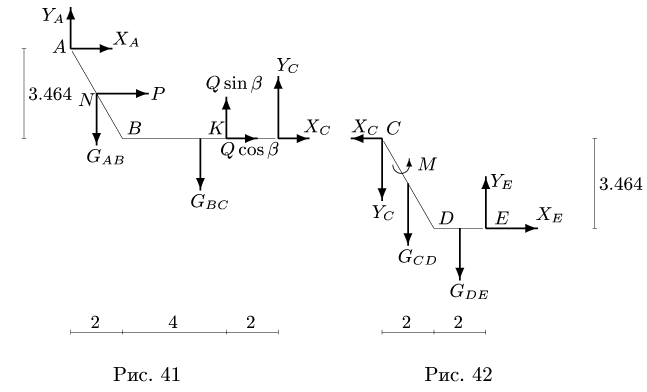
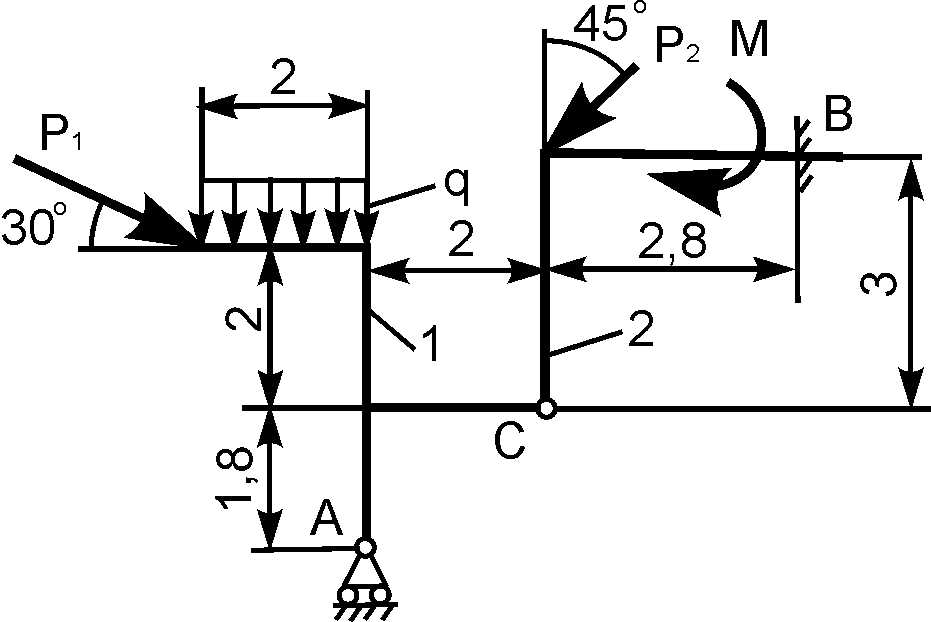
1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.
В точке А прикладываем реакции 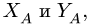
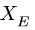
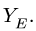
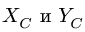
Система уравнений равновесия двух тел, образованных при разбиении, замыкается — имеем шесть уравнений равновесия (по три уравнения на каждую часть) и шесть неизвестных
2. Для каждой отдельной части составляем по три уравнения равновесия:
3. Решаем систему (1-6) относительно неизвестных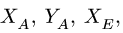
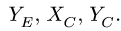
Если для решения использовать компьютер, систему лучше записать в матричном виде, предварительно вычислив правые части системы (1-6) и коэффициенты при неизвестных. Величины сил тяжести участков вычисляем через погонный вес 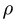
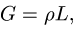
Система (1-6) имеет следующий матричный вид:
2.4.Расчет составной конструкции
Результаты расчетов в кН заносим в таблицу:
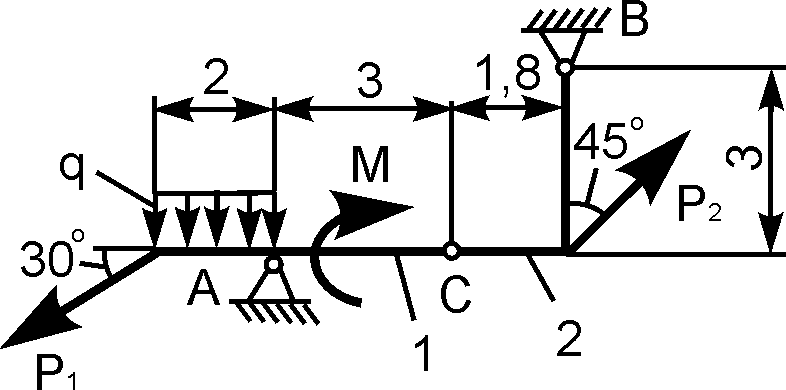
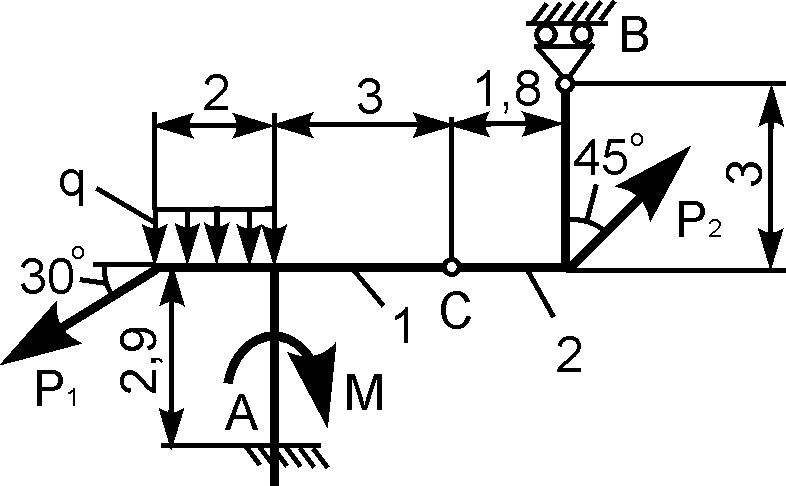
4. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы (рис. 43):
2-й способ:
1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.
2. Относительно шарнира С для каждой части конструкции составляем уравнения моментов (3) и (6). Для всей системы в целом составляем уравнения моментов (7,8) относительно опор А и Е.
3. Решаем систему четырех уравнений (3,6,7,8) относительно четырех неизвестных, замечая, что система распадается на две: уравнения (3) и (7) для 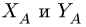
4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы (рис. 43):
2.5. Конструкция с распределенными нагрузками
Конструкция с распределенными нагрузками
постановка задачи. Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки и нагрузки, равномерно распределенной по дуге окружности.
План решения:
1. Внешние связи заменяем реакциями. Разбиваем систему на два тела по сочленяющему шарниру. К каждой из образовавшихся частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами равными по величине и противоположными по направлению.
2. Линейную нагрузку с максимальным значением 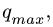
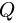
3. Нагрузку q, равномерно распределенную по дуге окружности радиусом R с центральным углом 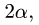
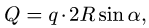
4. Для каждого тела составляем по три уравнения равновесия.
5. Решаем систему шести уравнений. Определяем реакции опор.
6. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы.
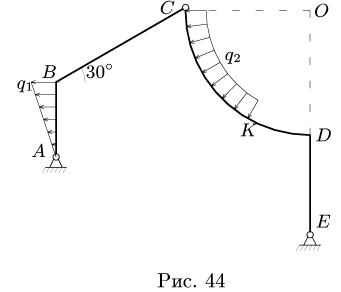
Задача №2
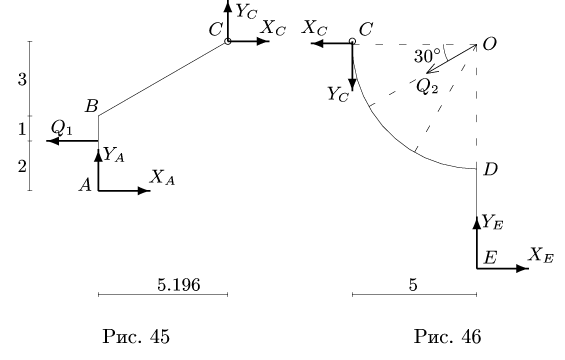
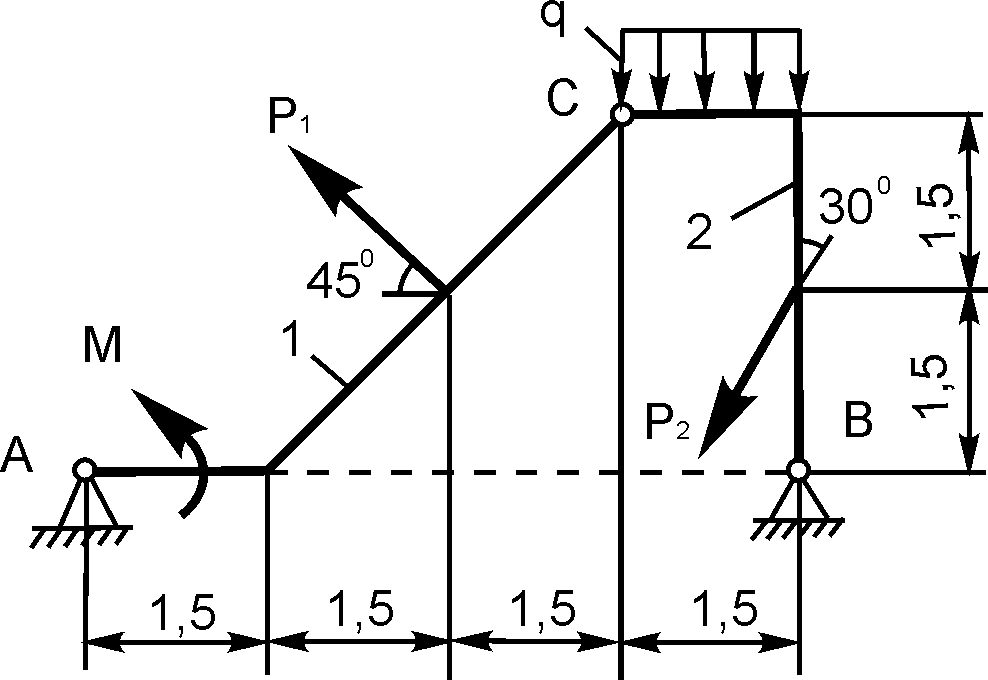
Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки с максимальной интенсивностью 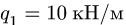
и нагрузки с интенсивностью 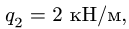
Решение
1. Внешние связи заменяем реакциями 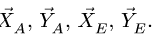
При разбиении по шарниру к каждой из частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами, равными по величине и противоположными по направлению.
2. Нагрузку, распределенную по линейному закону, заменяем сосредоточенной 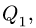
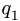
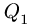
3. Нагрузку с интенсивностью 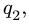
направленной по биссектрисе угла 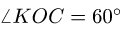
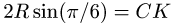
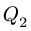
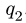
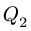
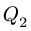
4. Составляем уравнения равновесия частей рамы:
5. Решаем систему (1) шести уравнений с шестью неизвестными. Результаты расчетов в кН заносим в таблицу:
Гл.2.Произвольная плоская система сил
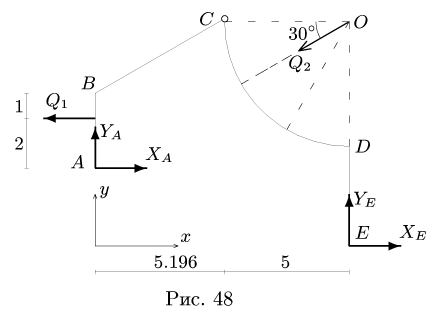
6. Выполняем проверку решения — составляем уравнения моментов для всей системы в целом (рис. 48):
Замечание. Можно предложить второй способ решения задачи, рассмотренный в предыдущем параграфе (с. 54). Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения С. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом (рис. 48).
Для данного примера это уравнения моментов относительно опорных шарниров А и Е.
Расчет системы трех тел, соединенных шарниром
Постановка задачи. Определить реакции опор конструкции, состоящей из трех тел, соединенных в одной точке шарниром.
План решения:
1. Расчленяем конструкцию на три отдельных тела и сочленяющий шарнир в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира, действие оси шарнира на тело заменяем ее реакциями.
2. Записываем по три уравнения равновесия для каждого из тел и два уравнения равновесия в проекциях для системы сил, приложенных к оси шарнира.
3. Решаем систему 11 уравнений с 11 неизвестными.
4. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной конструкции.
Задача №3
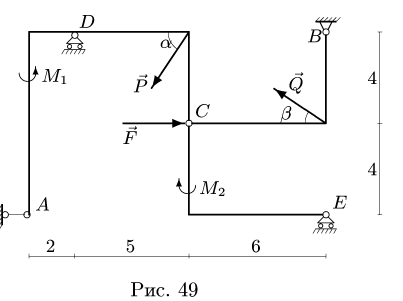
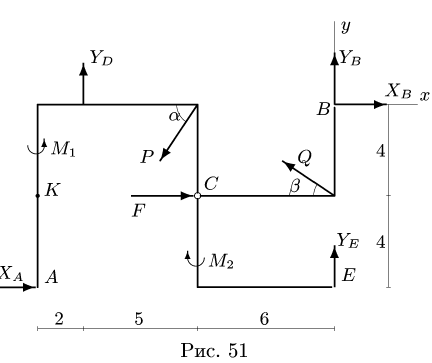
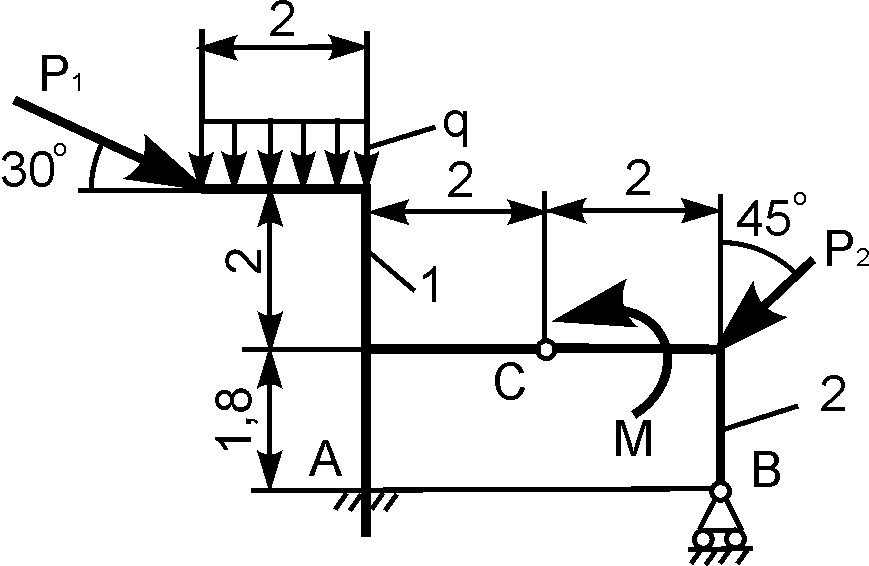
Определить реакции опор конструкции, состоящей из трех тел, соединенных в точке С шарниром. В точке В конструкция опирается на неподвижный шарнир, в точках D и Е — подвижные шарниры, в точке А — горизонтальный опорный стержень. На конструкцию действуют силы F — 40 кН, Р — 20 кН, Q — 10 кН и сосредоточенные моменты 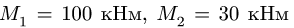
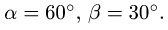
Решение
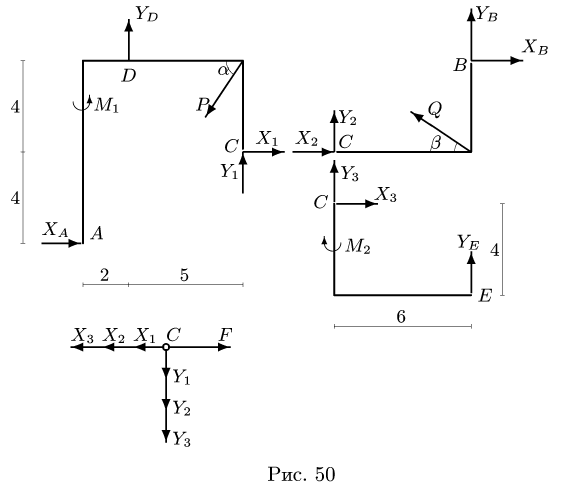
1. Расчленяем конструкцию на три отдельных тела ADC, СВ, СЕ и сочленяющий шарнир С в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира С, действие оси шарнира на тело заменяем ее реакциями (рис. 50).
2. Для каждого из тел (АС, ВС, ЕС) записываем по три уравнения равновесия — два уравнения проекций и уравнение моментов относительно точки С 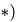
4. Решаем систему 11 уравнений с 11 неизвестными четов в кН записываем в таблицу:
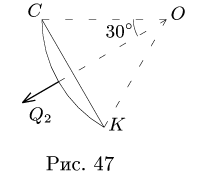
5. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной системы (рис. 51). Моментную точку К выбираем так, чтобы в уравнения вошли все проверяемые величины
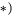
Замечание. Предложенный способ расчета не является единственным. Например, если из трех частей, соединенных в одном шарнире, можно отделить одну, имеющую в качестве опоры подвижный шарнир (часть СЕ, рис. 50), то получится система двух тел, одно из которых (СЕ) имеет три неизвестные реакции. Определить эти реакции можно из системы трех уравнений равновесия этой части.
Затем следует рассмотреть оставшуюся часть, состоящую их двух еще нерасчлененных тел. В качестве дополнительной нагрузки к ним будет приложены (в противоположную сторону) две реакции отброшенной третьей части.
- Момент силы относительно оси
- Равновесие вала
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Определение передаточных отношений различных передач
- Задачи на поступательное движение тела
- Задачи на вращательное движение тела
- Равновесие тяжелой рамы
Статически
определимые задачи
– задачи, в которых реакции внешних
связей находятся из уравнений равновесия.
В
Рис. 1.60
таких задачах число
неизвестных реакций равно числу уравнений
равновесия, которые могут быть составлены
для механической системы (рис. 1.60).
Дано:
Р, М, q.
Определить реакции внешних связей в
точках А и В.
Порядок
решения таких задач рассмотрен ранее,
поэтому сразу же записывают уравнения
равновесия для плоской произвольной
системы сил:
∑ Fix
= 0 = XА
– RBsinα
= 0; (1)
∑ FiY
= 0 = YA
– Q
– P
+ RBcosα
= 0; (2)
∑ MiA
= 0 = – Q·1
– P·4
– M
+ RBsinα·3,5tgα
+ RBcosα·7,5
= 0. (3)
Очевидно,
что из трех уравнений равновесия легко
находятся реакции внешних связей XA,
YA,
RB.
Статически
неопределимые задачи
– задачи, в которых реакции внешних
связей не могут быть найдены из уравнений
статического равновесия, составленных
для данной механической системы.
Для
балки (рис. 1.61) можно составить только
три уравнения равновесия, в которые
входят четыре неизвестные реакции XA,
YA,
XB,
YB.
Рис. 1.61
Дано:
Р, М, q.
Определить реакции внешних связей в
точках А и В.
Подробное
решение такой задачи (статически
неопределимой) рассматривается в курсе
сопротивления материалов.
1.23. Алгоритм решения задач на определение реакций внешних связей для составных конструкций
Существует
целый класс задач на равновесие составной
конструкции, которые могут быть решены
методами статики твердого тела. Решение
таких задач проводится по следующему
алгоритму.
-
Выбирается
система отсчета. -
Выделяется
механическая система (составная
конструкция), равновесие которой
рассматривается. -
К
механической системе прикладываются
активные нагрузки. Если задана
распределенная нагрузка, то она
приводится к сосредоточенной силе. -
Согласно
аксиоме связей внешние связи, наложенные
на механическую систему, отбрасывают,
и действие их заменяют соответствующими
реакциями. -
Записываются
уравнения равновесия, соответствующие
системе сил, действующей на составную
конструкцию (система активных сил и
реакций внешних связей). -
Установив,
что число неизвестных реакций внешних
связей превышает число уравнений
равновесия, составную конструкцию
расчленяют по внутренним связям. -
Рассматривают
равновесие каждого из тел составной
конструкции, которое находится в покое
под действием активных сил, реакций
внешних связей и реакций внутренних
связей. -
Для
каждого из тел конструкции записывают
соответствующие уравнения равновесия. -
Полученную
систему уравнений решают в наиболее
удобной последовательности и находят
неизвестные реакции внешних и внутренних
связей.
Обычно
при расчете используются не все уравнения
равновесия, составленные для механической
системы и для каждого из тел в отдельности.
Поэтому оставшиеся уравнения используют
для проверки полученных результатов.
1.24. Варианты курсового задания с 3 «Определение реакций опор составной конструкции (система двух тел)»
Методологию
расчета реакций внешних связей, наложенных
на составную конструкцию, рассмотрим
на примере выполнения курсового задания
С 3, которое входит в контрольную работу
обучающегося.
Конструкция
состоит из двух тел. Определить реакции
внешних связей, наложенных на составную
конструкцию. Варианты расчетных схем
конструкций и приложенные к ним нагрузки
приведены в табл. 1.3.
Таблица 1.3
|
Номер варианта |
Расчетная |
Исходные данные |
Определяемые величины |
|
1 |
2 |
3 |
4 |
|
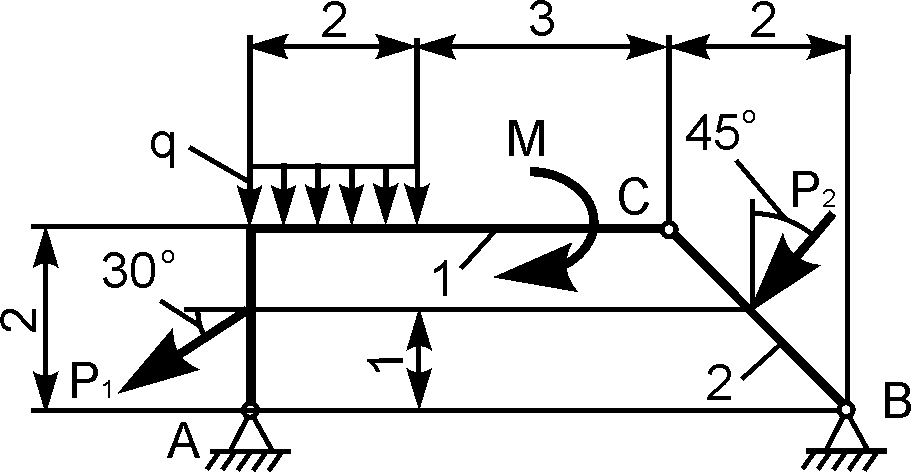
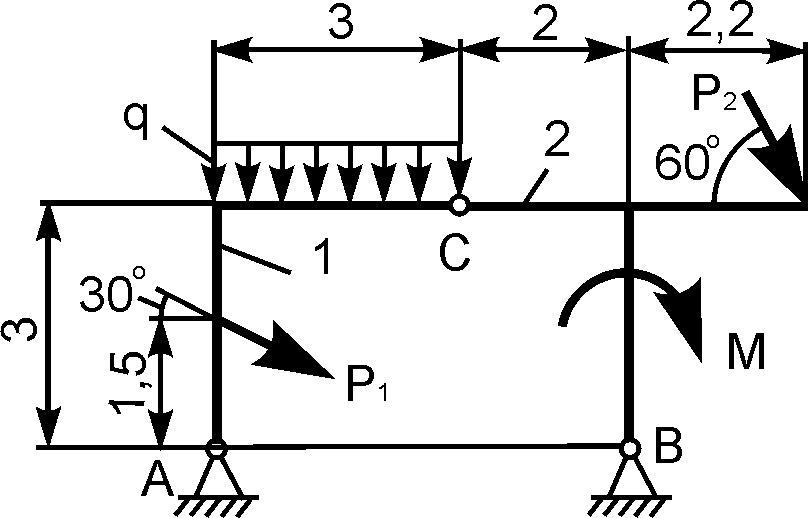
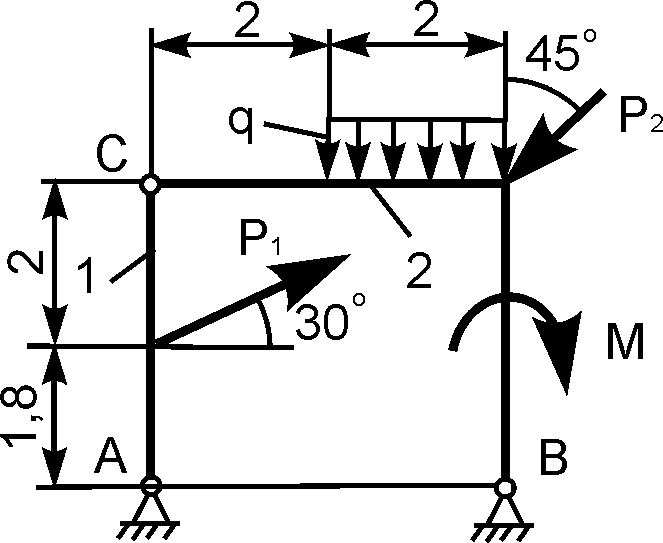
1 |
|
Р1
Р2 М = 6 кН·м;
q |
XA
YA
XВ
YВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
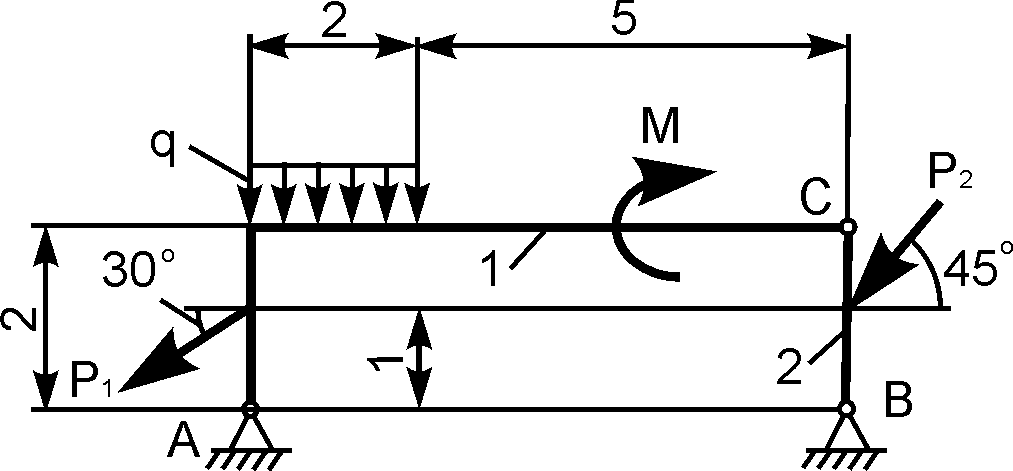
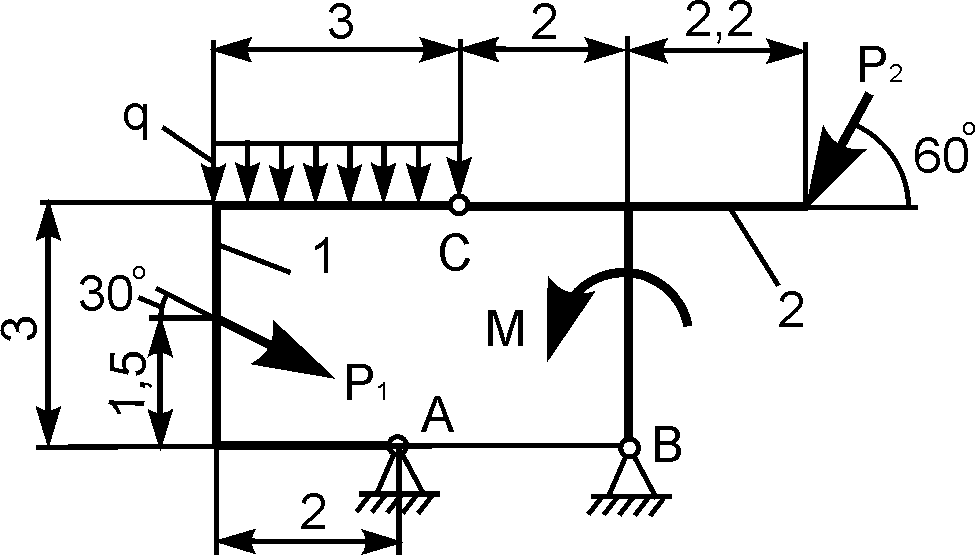
2 |
|
Р1
Р2
М = 12
q |
XA
YA
XВ
YВ |
|
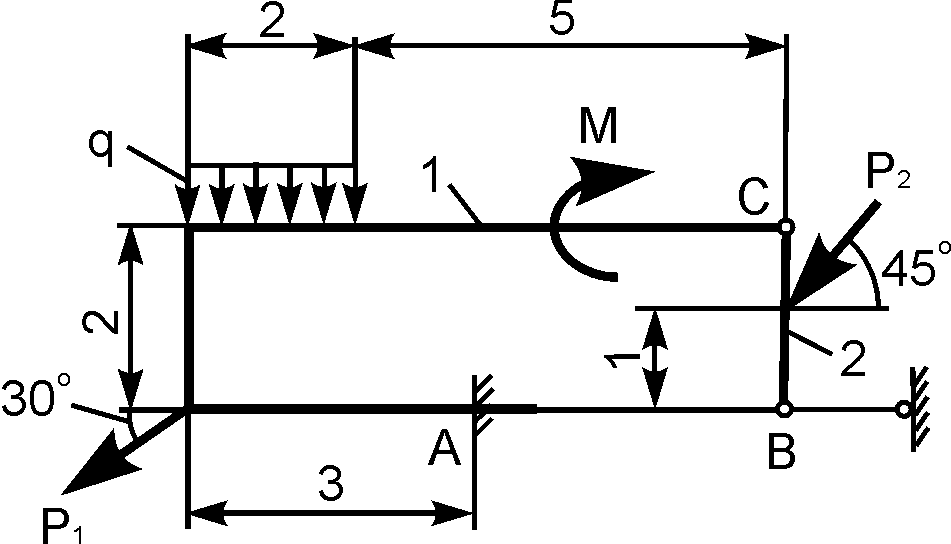
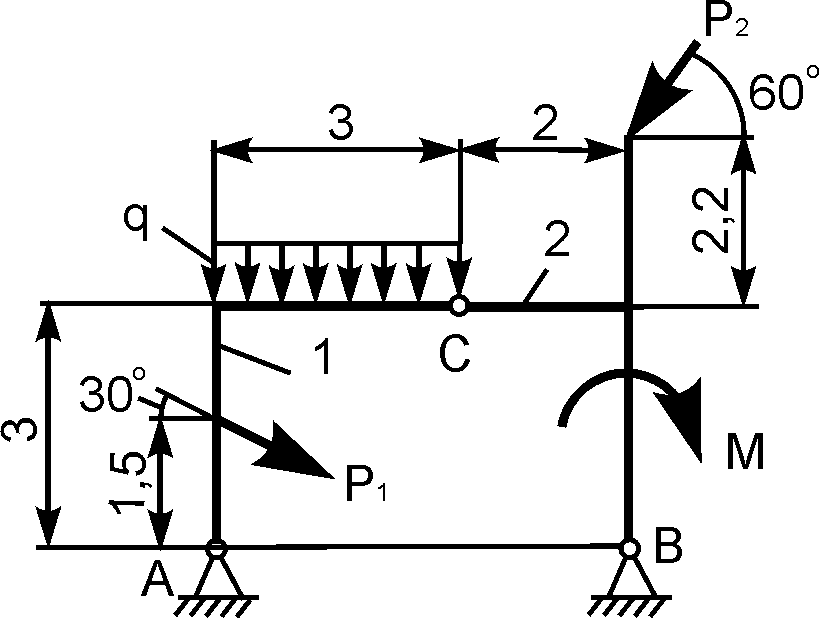
3 |
|
Р1
Р2
М = 3
q |
XA
YA
XВ
YВ |
|
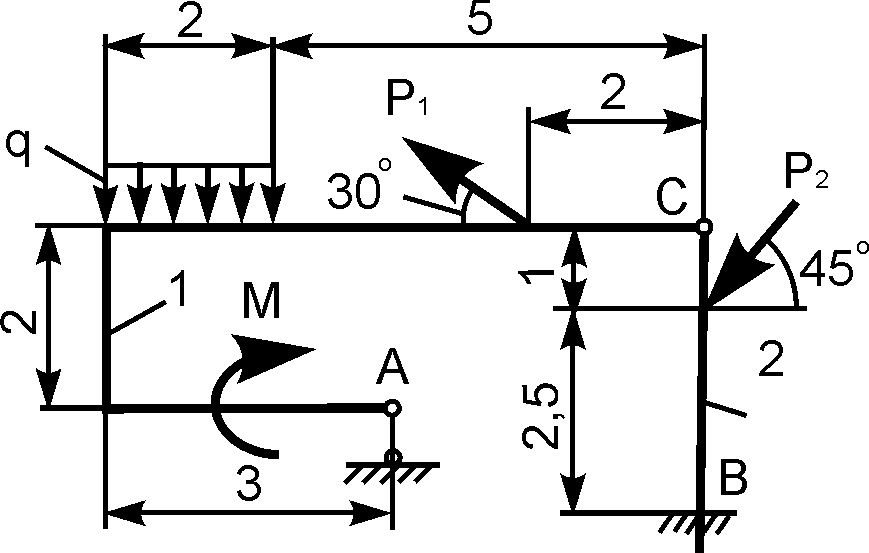
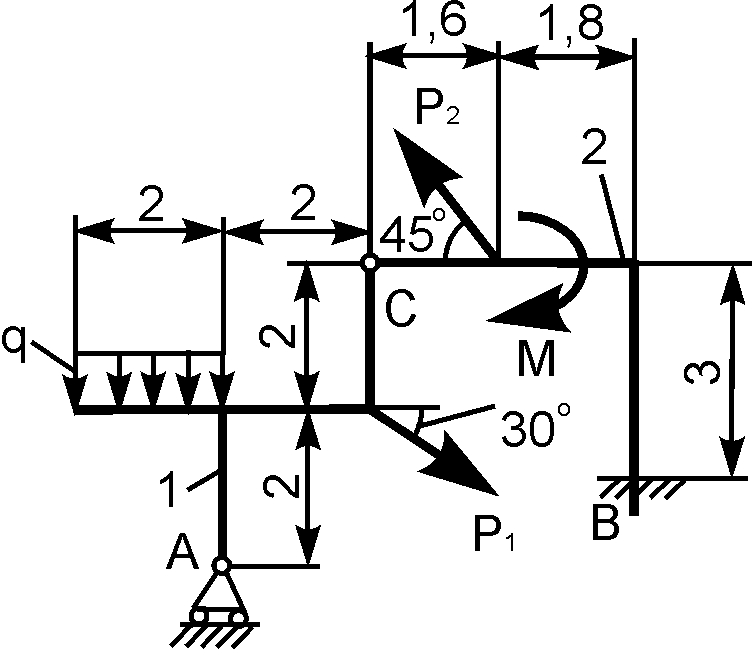
4 |
|
Р1
Р2 М = 4 кН·м;
q |
XA
YA
XВ
YВ |
|
5 |
|
Р1
Р2 М = 3 кН·м;
q |
XA
YA
MA
RВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
6 |
|
Р1
Р2 М = 10 кН·м;
q |
RA
XB
YВ
MВ |
|
7 |
|
Р1
Р2 М = 15 кН·м;
q |
RA
XB
YВ
MВ |
|
8 |
|
Р1
Р2 М = 16 кН·м;
q |
XA
YA
XВ
YВ |
|
9 |
|
Р1
Р2 М = 6 кН·м;
q |
XA
YA
XВ
YВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
10 |
|
Р1
Р2
М = 9
q |
XA
YA
XВ
YВ |
|
11 |
|
Р1
Р2 М = 6 кН·м;
q |
RA
XB
YВ
MВ |
|
12 |
|
Р1
Р2 М = 8 кН·м;
q |
RA
XB
YВ
MВ |
|
13 |
|
Р1
Р2 М = 8 кН·м;
q |
XA
YA
XВ
YВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
14 |
|
Р1
Р2 М = 12 кН·м;
q |
XA
YA
XВ
YВ |
|
15 |
|
Р1
Р2 М = 5 кН·м;
q |
XA
YA
MA
RВ |
|
16 |
|
Р1
Р2 М = 4 кН·м;
q |
XA
YA
MA
RВ |
|
17 |
|
Р1
Р2 М = 6 кН·м;
q |
XA
YA
XВ
YВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
18 |
|
Р1
Р2 М = 4 кН·м;
q |
XA
YA
XВ
YВ |
|
19 |
|
Р1
Р2 М = 12 кН·м;
q |
XA
YA
XВ
YВ |
|
20 |
|
Р1
Р2 М = 8 кН·м;
q |
XA
YA
MA
RВ |
|
21 |
|
Р1
Р2 М = 12 кН·м;
q |
XA
YA
XВ
YВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
22 |
|
Р1
Р2 М = 10 кН·м;
q |
XA
YA
MA
RВ |
|
23 |
|
Р1
Р2 М = 5 кН·м;
q |
RA
XB
YВ
MВ |
|
24 |
|
Р1
Р2 М = 12 кН·м;
q |
XA
YA
MA
RВ |
|
25 |
|
Р1
Р2 М = 8 кН·м;
q |
XA
YA
MA
RВ |
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
26 |
|
Р1
Р2 М = 6 кН·м;
q |
RA
XB
YВ
MВ |
|
27 |
|
Р1
Р2 М = 4 кН·м;
q |
XA
YA
XВ
YВ |
|
28 |
|
Р1
Р2 М = 8 кН·м;
q |
XA
YA
MA
RВ |
|
29 |
|
Р1
Р2 М = 6 кН·м;
q |
XA
YA
MA
RВ |
Окончание табл. 1.3
|
1 |
2 |
3 |
4 |
|
30 |
|
Р1
Р2 М = 6 кН·м;
q |
RA
XB
YВ
MВ |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Айрат Хамитов
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Задачи статики
Рассмотрим примеры с системой двух и более тел. Реакции, возникающие от наложенных связей, являются для нас неизвестной величиной. Их количество зависит от наложенных связей. Если количество реакций, которые являются неизвестными, меньше числа независимых уравнений статики, то система может быть решена.
Соответственно мы можем разделить все конструкции на:
- статически определенные. Примерами подобных систем могут служить арки, фермы, балки, многопролетные балки;
- статически неопределенные, в которых тела являются неопределимыми. Образцом подобной конструкции может быть груз, закрепленный на 3 нитях, которые располагаются в одной области. При рассмотрении точки равновесия составляются 2 независимых уравнения, а неизвестных реакций будет 3 (от силы натяжения каждой из нитей).
Рассчитывая примеры из статики, определяют реакции опоры сочлененной системы, которая состоит из более чем одного тела. Частным примером такой системы является неразрезная балка. Две части системы будут соединение внутренними связями. Связи, которые называют внешними, соединяют систему из двух тел с другими телами, которые не входят в систему.
Особенность рассматриваемых конструкций заключается в том, что, убрав внешние связи система теряет жесткость, например, части могут переворачиваться вокруг шарниров.
Определение 1
Шарнир – тип опоры или соединения, которое обеспечивает движение вокруг оси или точки.
Для решения пользуются методом расчленения, он позволяет собрать необходимое число уравнений.
Для поиска решения используют один из двух способов:
- согласно первому способу, конструкцию, которая состоит из нескольких тел освобождают от внешних связей, на схеме показывают активные силы и реакции, которые остаются после отбрасывания внешних связей. На основании схемы составляют уравнение равновесия системы сил, действующих на конструкцию. Затем отбрасываются связи внутри системы, рассматривая равновесие первой части конструкции, собираются уравнения равновесия для недостающей части. Получается, что число собранных уравнений равно числу неизвестных, соответственно, решив все уравнения, будут найдены искомые величины;
- согласно второму методу решения, конструкция освобождается от внешних и внутренних связей и разделяется на составные части. Для частей системы составляется рабочая схема, на которой показывают активные силы и реакции всех отброшенных связей. Для частей конструкции составляется уравнение равновесия и проверяется статическая определимость. После совместного решения всех уравнений будут найдены искомые величины.
«Определение реакций опор составной конструкции: система двух тел» 👇
Расчет реакций опор в составных конструкциях
Стандартной задачей будет определение реакции связей внутри и снаружи системы из двух тел. В качестве исходных данных выдается схема, с указанием расположения системы тел и типа опор.
Решение задачи ведется по следующему алгоритму:
- формируем упрощенную схему, указав нагрузки извне, все размеры и типы опор. Если в условиях приведена равномерно распределенная нагрузка, то заменяем ее сосредоточенной силой, которая приложена в середине элемента;
- условно отбрасываем внешние связи, на схеме показываем их реакциями;
- собираем уравнение равновесия полученной плоской системы, так как в трех уравнениях равновесия используется большее, чем количество уравнений неизвестных, то необходимо рассмотреть части конструкции по отдельности;
- отбрасываем связи внутри и рассматриваем равновесие одной из частей, с учетом активных сил и связей, которые были отброшены, составляем три уравнения равновесия, которые будут содержать два дополнительных неизвестных. Из шести полученных уравнений находим все 6 неизвестных;
- проверяем правильно полученных значений, подставляя найденные значения в уравнения.
Рисунок 1. Пример расчета двухсоставной конструкции. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Уравнения равновесия для каждой из частей системы. Автор24 — интернет-биржа студенческих работ
Деля систему на две части, связи внутри нее в каждой части показывают противоположно направленными.
После определения всех неизвестных данные заносятся в таблицу. Если в результате проверки обнаружиться ошибка, то необходимо вернуться на этап составления уравнений. Все собранные уравнения равновесия должны соответствовать составленной конструкции.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме