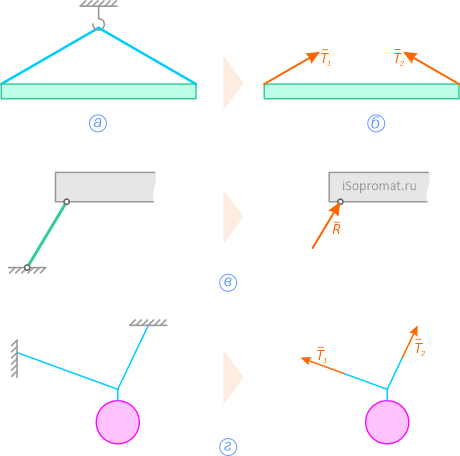
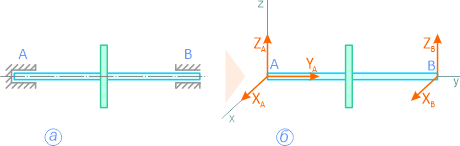
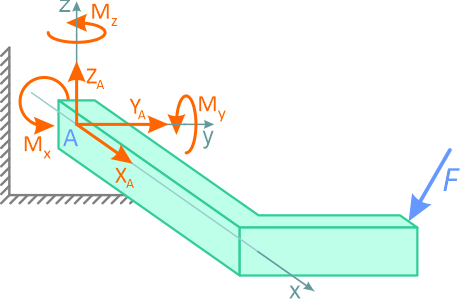
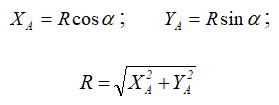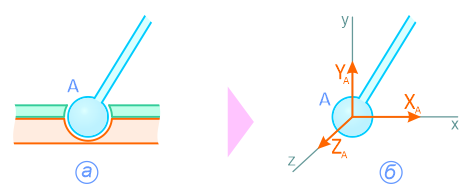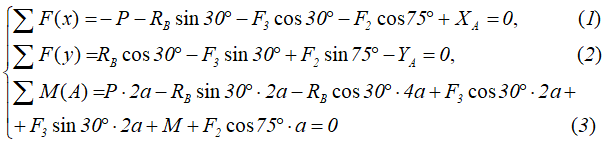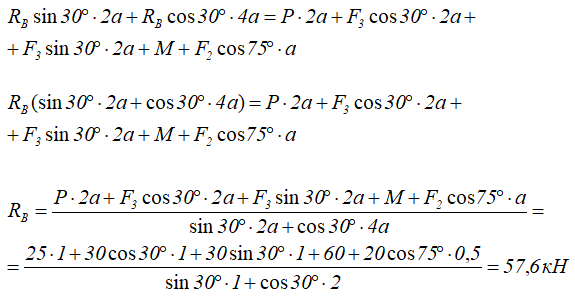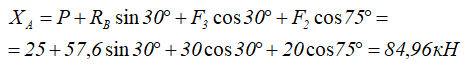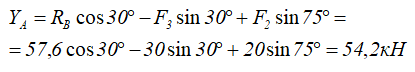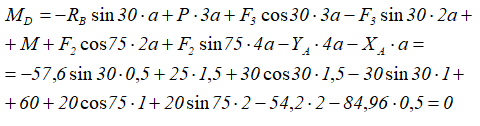Методика решения задач плоской системы сходящихся сил
1. Число неизвестных в данных задачах не превышает двух.
2. Рассматриваем точку, находящуюся в равновесии.
3. Определяем наличие активных сил.
4. Освобождаемся от связей и заменяем их реакциями.
5. Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.
6. Решаем уравнения равновесия относительно неизвестных.
7. Выполняем проверку.


Решение.
I. Аналитическое решение
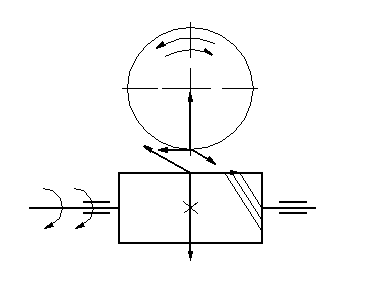
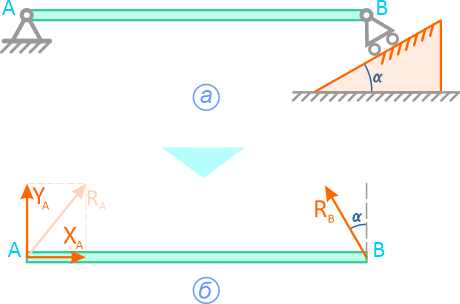
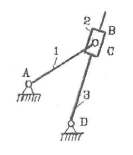
1. Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.
2. Выбираем систему координат хОу и составляем таблицу, уравнения равновесия.
| силы |  =0 =0 |
 =0 =0 |
| R1 |  |
 |
| R2 |  |
 |
| F1 |  |
3. Составляем систему уравнения и решаем.
Проверка: 


II. Графическое решение.
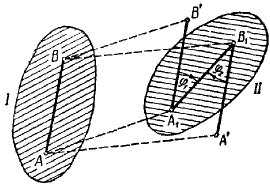
1. Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F1.
2. Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R1+R2+F1=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R1 и R2 до их пересечения.
3. Определяем реакции связей R1 и R2 , умножая полученные результате графического построения отрезки на масштаб.
4. Проверка: Заключается в сравнении значений векторов R1 и R2 , найденных аналитическим и графическим способами. r1 = (R1а — R1б)/ R1а; r1 = (R2а — R2б)/ R2а;
Задания для выполнения работы
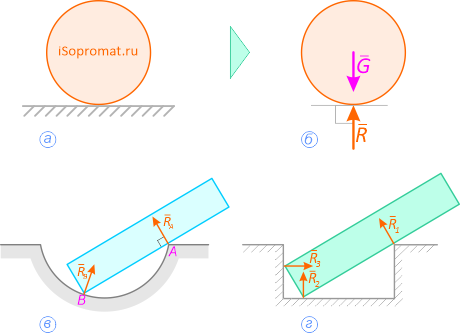
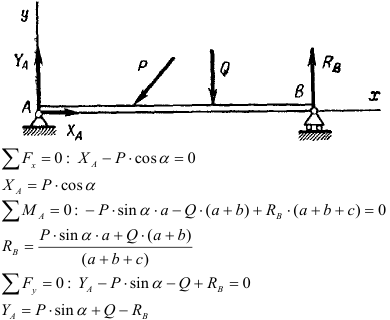
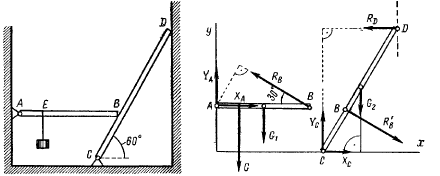
Груз, силой тяжести G удерживается в равновесии с помощью связей. Определить реакции связей, удерживающих груз аналитически и графически.
Контрольные вопросы:
1. В чем отличие между осью и проекцией?
2. Сколько уравнений равновесия Вы составляли при решении задачи?
3. Методика решения задач ПССС.
4. Дайте определение плоской системе сходящихся сил.
5. Какой величиной является проекция силы на координатную плоскость?
Литература:
1. Вереин Л.И. Техническая механика – М: Академия, 2006.
2. Мовнин М.С. Основы технической механики – СПБ: Политехника, 2003.
3. Молчанова Е.В., Шурыгина Г.Н. Статика и сопротивление материалов — Томск, 2008.
Практическая работа №3
Тема урока: Определение реакций в опорах с вертикальными нагрузками
Тип урока:закрепление полученных знаний.
Цель урока:Научиться определять реакции в опорах с вертикальными нагрузками
Обеспечивающие средства:
1. методическое руководство по выполнению работы;
3.тетрадь для практических работ;
4.карандаш, линейка, ластик, авторучка;
Технология работы:
1.Внимательно изучите методические указания, предложенный теоретический материал.
2.В соответствие с вариантом, выполнить задание по методике представленной ниже.
3.Сделайте выводы о проделанной работе.
4.Ответить на контрольные вопросы.
Теоретический материал


Момент –способность силы создавать вращение (М).
Единица измерения М [ Н * м] 1кНм = 10 3 Нм, 1мНм = 10 6 Нм
Момент силы относительно точки равен произведению силы на перпендикуляр, опущенный из точки вращения на линию действия силы.
а – плечо, перпендикуляр или кратчайшее расстояние между точкой вращения и линией действия силы.
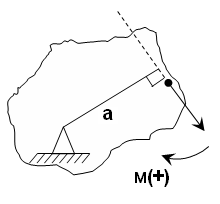


Момент силы относительно точки равен нулю, если линия действия силы проходит через точку вращения, т.к. плеча равно нулю, нет вращения.

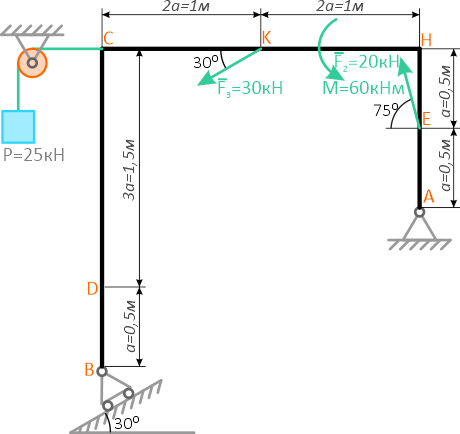
Решение.
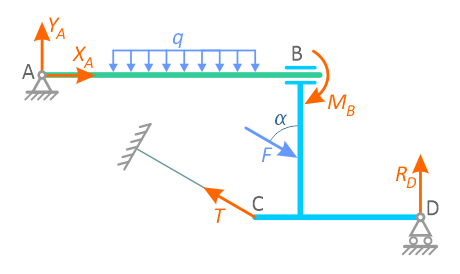
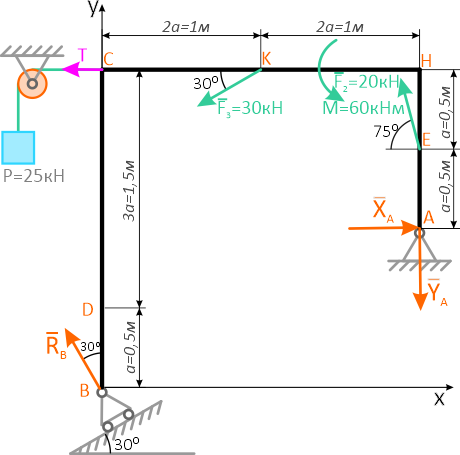
1. Определяем связи, заменяем их реакциями.
2. Определяем оси координат Х, У.
3. Составляем таблицу уравнения равновесия.

| Силы |  =0 =0 |
 =0 =0 |
 =0 =0  |
| RА | 6RA | RA | |
| RBY | -6RBY | RBY | |
| F1 | 2F1 | -4F1 | -F1 |
| F2 | -4F2 | 2F2 | F2 |
4. Составляем уравнение по II-ому виду
Из 1-го уравнения находим RBY
Из 2-го уравнения находим RA
5. Проверка: по 3-му уравнению 4,7+1,3-8+2=0
Техническая механика
Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
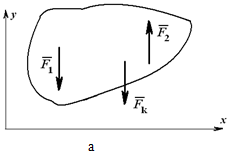
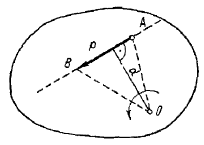
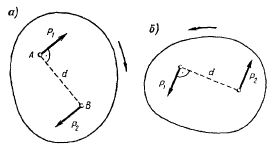
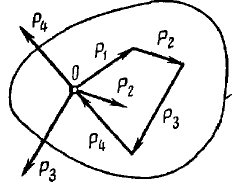
Пусть дана плоская система трех сил F1 , F2 и F3 , линии действия которых сходятся в точке А (см. рисунок а) .
На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А . Сложив первые две силы F1 и F2 по правилу параллелограмма, получим их равнодействующую R (см. рисунок а) :
R = F1 + F2 .
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3 :
где FΣ – равнодействующая данной системы трех сил.
Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
FΣ = F1 + F2 + F3 +…+ Fn .
Сокращенно это равенство можно записать так:
FΣ = ΣFi , где i – все целые числа от единицы до n .
Очевидно, что построения, выполненные на рисунке a , можно заменить более простым, как показано на рисунке b . Многоугольник АВСD называют силовым многоугольником. Сторона AD , соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b) .
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.
Геометрическое условие равновесия плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая FΣ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.
При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Пример решения задачи
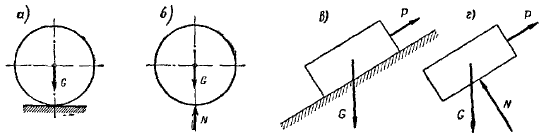
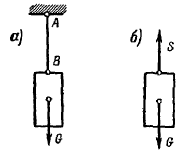
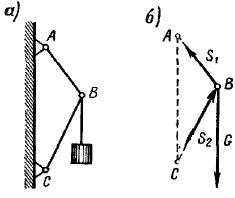
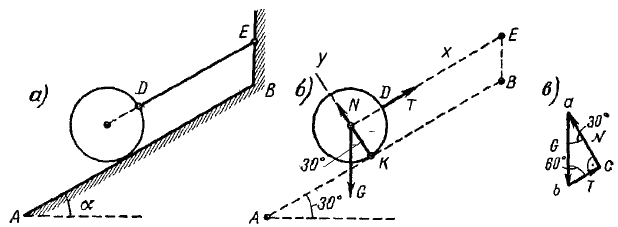
В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G .
Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:
ΣFi = 0 , или G + N + R = 0.
Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок) . Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:
N = G tg α ; R = G/cos α
Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R .
Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки) , причем согласно аксиоме взаимодействия:
Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.
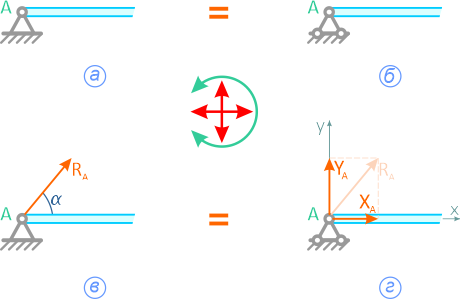
Проекция силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.
Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
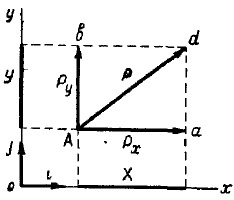
На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
Px = Pcos α, Py = Psin α .
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции — проекция, направленная в положительном направлении оси считается положительной, в противном случае — отрицательной.
Возможны два частных случая:
— если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку) ;
— если сила параллельна оси, то она проецируется на ось в натуральную величину.
Зная проекции силы на координатные оси, можно определить ее величину (модуль) , используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила — гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = Py/Px .
Отметим, что силу P можно представить, как равнодействующую двух составляющих сил Px и Py , параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция — алгебраическая.
Аналитический способ определения равнодействующей плоской системы сил
Пусть дана плоская система сходящихся сил F1, F2, F3, F4. Fn .
Равнодействующая этой системы FΣ = ΣFi .
В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. FΣx = ΣFix .
Правую часть этого равенства можно представить упрощенно: FΣx = ΣX .
Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y , алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:
Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:
FΣ = √(FΣx 2 + FΣy 2 ) (здесь и далее √ — знак корня);
Направляющий тангенс угла между вектором FΣ и осью x :
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Аналитические условия равновесия плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:
Учитывая, что FΣx = ΣX; FΣy = ΣY , получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:
Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.
Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.
iSopromat.ru
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Другие условия равновесия
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
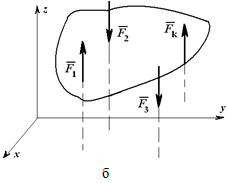
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Российский
химико-технологический университет
имени
Д.
И. Менделеева
Кафедра
прикладной механики
Курсовая
работа
Тема:
«Изгиб»
Работу
выполнил: Chipits,
гр. П-11
Работу
проверил доцент Соколов-Бородкин Евгений
Сергеевич
Задача
1:
Дано:
Wx
= 160 cм3
L
= 1,8 м
1
эпюры Qy
и
Mx
Определить:
2)
положение опасного сечения
3)несущую
способность конструкции q,P,M
Решение:
1)Используя
метод сечений и правила знаков при
изгибе, найдем силы Qy
и изгибающие моменты Mx:
Участок
1-1:
Участок
2-2:
Участок
3-3:
2)
Опасное сечение – точка С, т.к. там момент
Mx
достигает
своего максимального значения
3)Из
условия прочности найдем параметры
q,P,M
:
Условие
прочности :
Отсюда:
Пересчитаем
значения Qy
и Mx
в узловых точках эпюр:
На
участке КВ:
В
точке K:
В
точке B:
На
участке КС:
В
точке В:
В
точке С:
На
участке КD:
В
точке C:
В
точке D:
Построим
эпюры Qy
и Mx:

Задача
2:
Дано:
q
= 8 кН/м
L
= 1,2
м
σт=230
МПа
n=1,3
[τ]=70
МПа
1
Определить
Rdy,Rbx,Rby
2)
Построить эпюры Qy
и Mx
3)
Определить Акруг,
Апрям,
Адвут
4)
Определить оптимальное сечение
5)Проверить
прочность по касательным напряжениям
Решение:
1)
Определим опорные реакции:
А)Из
условия
:
Б)
Из условия
:
В
этом уравнении две неизвестные величины,
поэтому найдем Rdy
из условия
:
Найдем
Rby:
Следовательно,
сила Rby
направлена в другую сторону.
2)Найдем
силы Qy
и моменты Mx
на участках согласно правилу знаков
для Qy
и Mx
при
изгибе:
Участок
1-1:
Участок
2—2:
Участок
3—3:
Построим
эпюры поперечных сил Qy
и изгибающих моментов Mx:
3)Определим
из условия прочности размеры поперечного
сечения:
Найдем
размеры сечения в виде:
А)круга:
Б)прямоугольника:
В)двутавра:
Поскольку
,
то выбираем двутавр №24а, его характеристики:
|
№ |
h,мм |
b,мм |
s,мм |
t,мм |
A,см2 |
Ix,cм4 |
Wx,см3 |
Sx,см3 |
|
24а |
240 |
125 |
5,6 |
9,8 |
37,5 |
3800 |
317 |
178 |
Адвут
=37,5
см2
4)Найдем
предельный момент сопротивления:
Из
сопоставления площадей и предельных
моментов сопротивления:
Следует,
что наименее металлоемкой окажется
двутавровая балка
5)Проверим
прочность трех расчетных сечений по
касательным напряжениям:
А)для
круглого сечения:
Б)для
прямоугольного сечения:

двутавра:
13
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «Техническая механика».
Лекции подготовлены для студентов любых специальностей и охватывают полностью предмет «техническая механика».
В лекциях вы найдёте основные законы, теоремы, правила и примеры.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в техническую механику
Техническая механика — это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.
Механическим движением — называется перемещение тела но отношению к другому телу, происходящее в пространстве и во времени.
Курс технической механики делится на три раздела: статику, кинематику и динамику.
Статика
Статикой называется раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому гелу.
Классификации нагрузок
Важнейшим понятием технической механики является понятие нагрузки.
Взаимодействие двух тел, способное изменить их кинематическое состояние, назы вается меха ни ческим взаимодействием.
Нагрузка — это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.
В механике встречается два вида нагрузки
- сила
- момент (пара сил)
Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения.
Сила изображается вектором. Прямая, по которой направлена данная сила, называется линией действия силы. За единицу силы в Международной системе единиц измерения СИ (в механике система МКС) принимается ньютон 
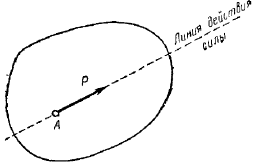
Моментом силы относительно некоторой точки на плоскости называется произведение модуля силы на ее плечо относительно этой точки, взятое со знаком плюс или минус:
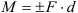
Плечом силы 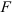
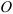
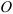
Момент силы относительно точки считается положительным, если сила 
Система двух равных по модулю, параллельных и противоположно направленных сил 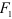
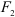
Расстояние 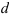
По характеру погружения
- сосредоточенные
- распределенные
По характеру воздействия на тело
- поверхностные
- объемные
По характеру изменения нагрузки во времени
- статические
- циклические
По форме возникновения
- активные
- реактивные
- инерционные
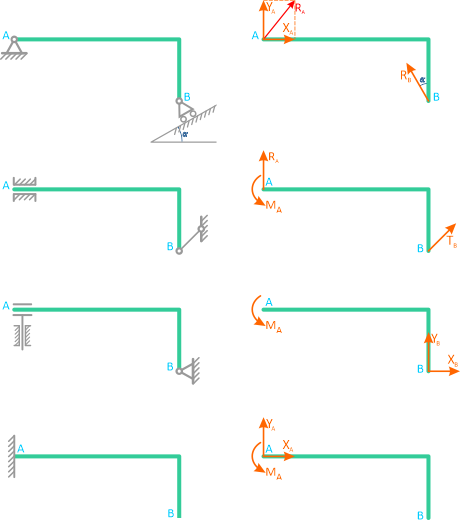
Классификации опор (реакции связей)
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело
Одним из основных положений механики является принцип освобождаем ост и твердых тел от связей, согласно которому несвободное твердое тело можно рассматривать как свободное, па которое, кроме задаваемых сил, действуют реакции связей.
Классификация реакций связей (реакций опор)
- гладкая плоскость
Реакция гладкой плоскости 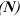
- гибкая связь
Реакция гибкой связи 
- жесткая связь
Реакция жесткой связи 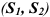
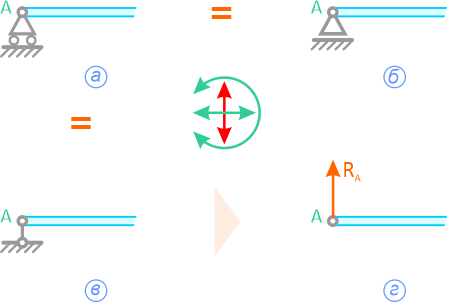
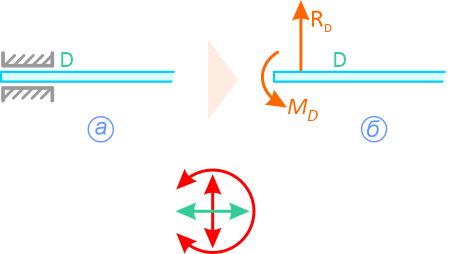
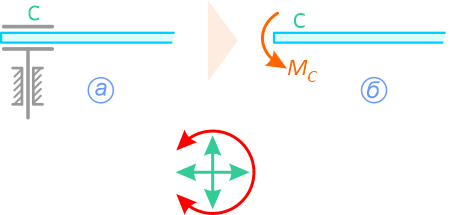
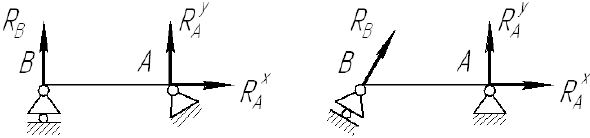
- шарнирно подвижная опора
Реакция шарнирно-подвижной опоры 
- шарнирно неподвижная опора
Направление реакции шарнирно-неподвижной опоры зависит от внешних сил, приложенных к системе. Данную реакцию задают двумя составляющими 
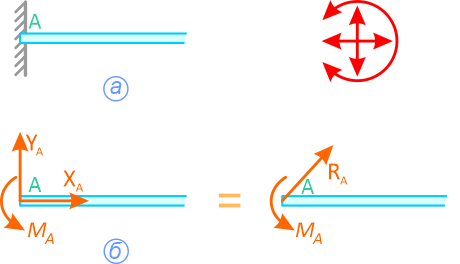
- жесткая заделка
Данную реакцию задают двумя составляющими, направленными перпендикулярно друг к другу и парой сил.
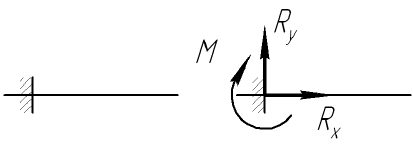
Проекции сил на оси
Взяв две взаимно перпендикулярные оси 
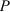
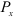
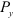
Силы 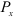
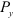
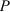
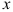
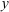
Проекция силы на ось определяется произведением модуля силы на косинус угла между направлениями оси и силы.
Если известны проекции силы на две взаимно перпендикулярные оси 
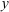
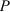
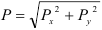
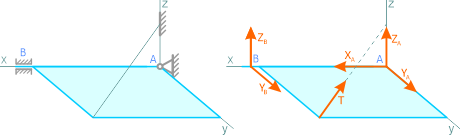
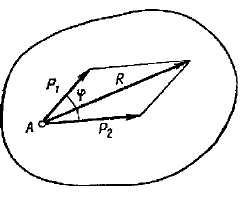
Сходящиеся силы. Условие равновесии системы сходящихся сил
Если к телу приложены несколько сил, линии действия которых пересекаются в одной точке то такие силы называются сходящимися.
Если к телу приложено несколько сил, то данные силы можно заменить одной силой, называемой равнодействующей, под действием которой тело будет находится в нагруженном состоянии эквивалентном заданной системе.
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
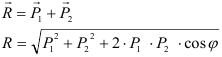
Сходящиеся силы уравновешиваются в том случае, если их равнодействующая равна нулю, т. е. многоугольник сил замкнут.
Пример:
Известно 
Спроектируем на ось 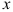
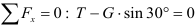
Спроектируем на ось 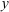
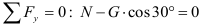
Условии равновесии статически определимых систем (уравнение проекций сил на оси и уравнение моментов)
Тело находится в равновесии, если сумма проекций, действующих на него сил на координатную ось равны 0.
Тело находится в равновесии, если сумма моментов сил относительно какой либо точки этого тела равны 0.
Для любого тела можно составить три уравнения равновесия
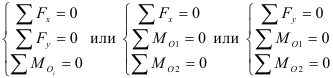
Статически определимой системой называется система, в которой число неизвестных не превышает числа уравнений равновесия.
Пример:
Пример:
Левая часть
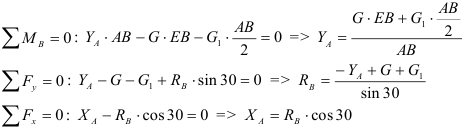
Правая часть
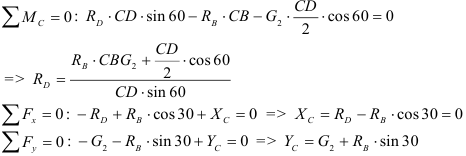
Кинематика
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Определение скорости и ускорении точки
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Ускорение точки — векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
Задание скорости и ускорения точки естественным способом
При задании точки естественным способом известен закон движения, выраженный зависимостью перемещения точки от времени
В этом случае скорость точки будет определяться как первая производная от данной зависимости
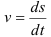
Ускорение точки будет определяться как вторая производная от зависимости перемещения или как первая производная от зависимости скорости
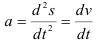
Пример:
Точка движется по окружности радиусом 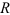
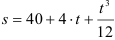
Определить скорость и ускорение точки в конце 3 секунды
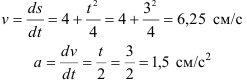
Задание скорости точки координатным способом
При задании точки координатным способом известны законы изменения координат данной точки в зависимости от времени 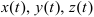
В этом случае скорость точки будет определяться как геометрическая сумма первых производных от данных зависимостей
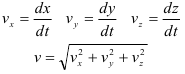
Ускорение точки будет определяться как геометрическая сумма первых производных от зависимостей скорости или вторых производных от зависимости изменения координат
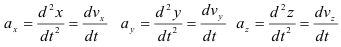
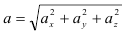
Пример:
Уравнения движения точки имеют вид
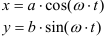
Определить уравнения скорости и ускорения данной точки
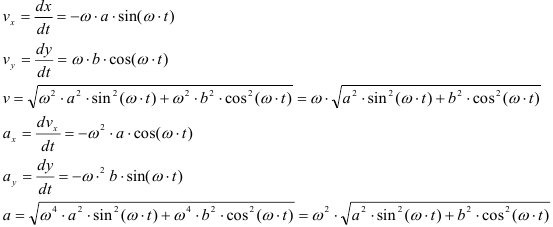
Если направление ускорения совпадает с направлением скорости (имеет одинаковый знак) то тело движется с положительным ускорением (ускоряется), если направление ускорения не совпадает с направлением скорости (имеет разные знаки) то тело движется с отрицательным ускорением (замедляется)
Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Все точки твердого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
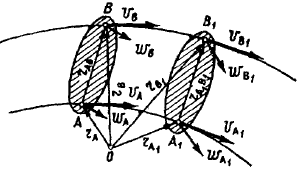
Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести 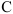
Для описания скорости и ускорения точки используются зависимости рассмотренные в предыдущем вопросе.
Вращательное движение
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой
Аналогом перемещения во вращательном движении является угол поворота 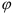
Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростью тела.
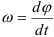
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
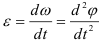
Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением. При этом, если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается равнозамедленным.
Рассмотрим движение точки 
Обозначим точку отсчета 
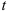
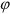
За время 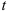
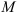
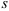
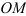
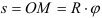
Скорость точки 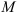
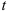
Величина окружной скорости определяется из выражения.
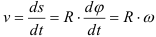
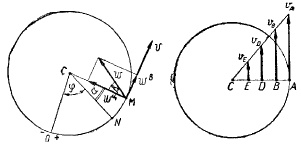
Из предыдущей формулы следует, что модули окружных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Ускорение точки 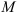
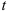
Тангенциальное ускорение направлено по касательной к окружности в точке 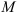
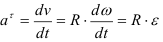
Нормальное ускорение направлено по радиусу окружности к её центру. Величина нормального ускорения определяется по зависимости
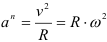
Полное ускорение точки определится из выражения
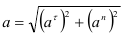
Пример:
Вращение маховика в период пуска машины определяется уравнением
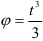
где 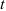
По уравнению вращения маховика находим его угловые скорость и ускорение
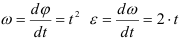
Определяем уравнение окружной скорости точки
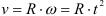
Выражаем отсюда время
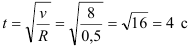
Определяем
Угловая скорость
Угловое ускорение
Тангенциальное ускорение
Нормальное ускорение
Полное ускорение
Возможно эта страница вам будет полезна:
Плоскопараллельное движение
Плоскопараллельным движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Так как положение плоской фигуры на плоскости вполне определяется положением двух ее точек или положением отрезка, соединяющего две точки этой фигуры, то движение плоской фигуры в ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости.
Предположим, что плоская фигура переместилась на плоскости из положения I в положение II. Отметим два положения отрезка 
Первый вариант. Переместим фигуру поступательно, из положения 
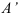
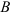
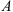
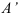
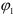
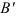
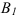
Второй вариант. Переместим фигуру поступательно из положения 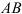
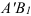
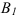
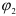
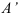
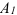
Как видно, поступательное перемещение плоской фигуры различно в различных вариантах, а величина угла поворота и направление поворота одинаковы, т. е.
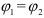
Из этого следует, что
Плоскопараллельное движение можно рассматривать как совокупность двух движении: поступательного движения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг полюса.
При этом поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.
Приняв за полюс некоторую точку 
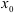
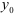
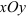
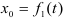
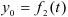
Вращательное движение фигуры относительно полюса можно описать уравнением
Определение скоростей точек плоском плоскопараллельное движение
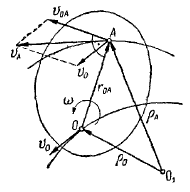
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
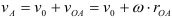
Для плоской фигуры совершающей плоскопараллельное движение в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.
Способы определения мгновенного центра скоростей
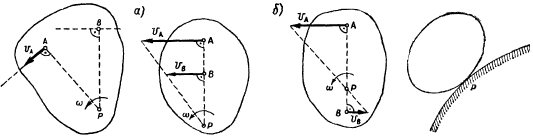
Определение скоростей точек плоской фигуры при помощи мгновенного центра скоростей
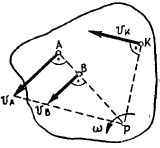
Определим скорости точек 
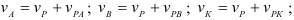
Если точка 
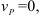
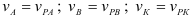
т. е. скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей; поэтому
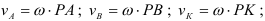
Пример:
Колесо радиусом 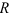
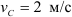
Определить скорости точек 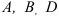
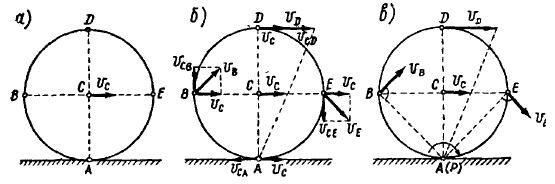
1-й вариант.
Примем за полюс центр колеса 
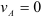
Точка 
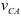
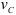
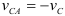
Расстояния от точек 
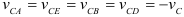
Откладывая в каждой точке скорость полюса 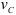
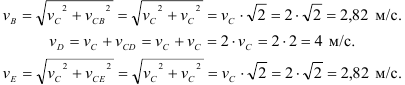
2-й вариант
Примем мгновенный центр скоростей колеса за полюс. Тогда скорости всех точек колеса определятся как вращательные скорости вокруг мгновенного центра скоростей.
Модули скоростей всех точек найдутся но пропорциональности скоростей их расстояниям от мгновенного центра скоростей: Найдем 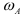
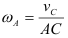
Тогда
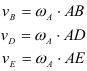
Обозначим радиус колеса через 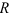
Тогда
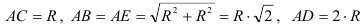
Тогда
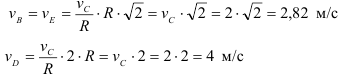
Возможно эта страница вам будет полезна:
Определение ускорений точек плоской фигуры совершающей плоскопараллельное движение
Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении вокруг полюса.
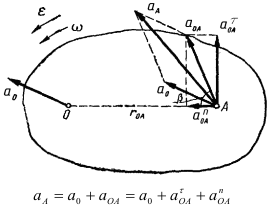
Пример:
Колесо радиусом 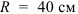
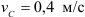
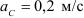
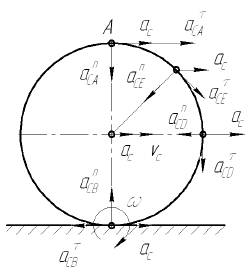
Определяем 
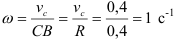
Определяем угловое ускорение.
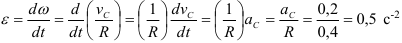
Для точки 
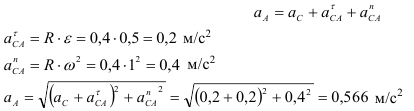
Для точки 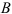
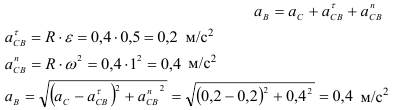
Для точки 
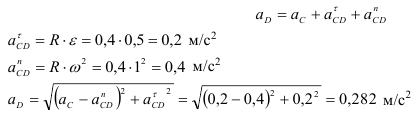
Для точки 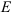
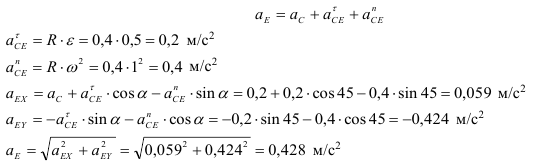
Разложение составного движении точки на относительное и переносное
Составное движение тонки (тела) — это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движениях.
Например, составное движение совершает лодка, переплывающая реку, пассажир, перемещающийся в вагоне движущегося поезда или по палубе плывущего парохода, а также человек, перемещающийся по лестнице движущегося эскалатора.
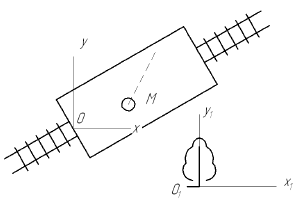
Через произвольную точку 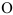
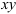
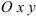
Неподвижной системой отсчета называют систему осей 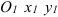
Движение точки 
Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозначают 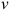
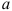
Движение точки 
Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением точки и обозначают 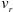
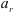
Движете подвижной системы отсчета 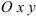
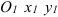

Скорость и ускорение точки тела 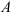

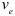
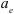
Движение точки 
Основная задача изучения составного движения состоит в установлении зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движений точки.
Возможно эта страница вам будет полезна:
Определение скоростей и ускорений точки при составном движении
Теорема сложения скоростей
Абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.
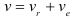
Для нахождения абсолютной скорости необходимо:
- Определить модуль и направление относительной скорости (в подвижной системе отсчета);
- Определить модуль и направление переносной скорости (скорость подвижной системы отсчета относительно неподвижной система отсчета);
- Определить геометрическую сумму относительной и переносной скоростей.
Теорема сложения ускорении
В случае непоступательного переносного движения абсолютное ускорение точки равно геометрической сумме переносного, относительного и ускорения Кориолиса.
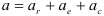
Поворотным ускорением (ускорением Кориолиса) называется составляющая абсолютного ускорения точки в составном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки:
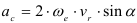
где 
Направление ускорения Кориолиса находится но правилу: Относительную скорость точки следует спроектировать на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90°, в сторону переносного вращения.
Ускорение Кориолиса равно нулю в трех случаях:
- если
, т.е. в случае поступательного переносного движения.
- если
, т.е. в случае относительного покоя точки или в моменты обращения в нуль относительной скорости движущейся точки;
- если
вектор относительной скорости перпендикулярен оси вращения в переносном движении.
Пример:
Вертикальный подъем вертолета происходит согласно уравнению 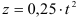
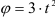
Свяжем подвижную систему отсчета с корпусом вертолета, неподвижную — с Землей. Относительное движение — вращение винта вокруг его оси является (это движение наблюдает пассажир вертолета, связанный с подвижной системой отсчета).
Переносное движение — является поступательное движение вертолета вертикально вверх.
Применяем теорему о сложении скоростей
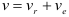
Относительная скорость точки 
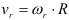
Если известен закон вращения винта 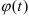
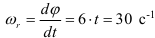
Тогда
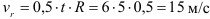
Вертолёт совершает поступательное движение. Переносная скорость точки 
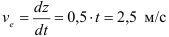
Так как
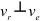
то
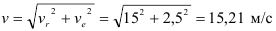
Применяем теорему о сложении ускорений
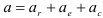
Винт совершает вращательное движение. Следовательно относительное ускорение точки 
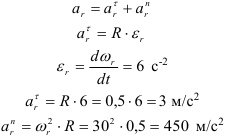
Переносная скорость точки 
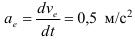
Ускорение Кориолиса равно нулю так как Вертолёт совершает поступательное движение 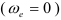
Так как 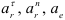
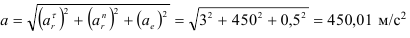
Пример:
Диск равномерно вращается с угловой скоростью 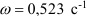
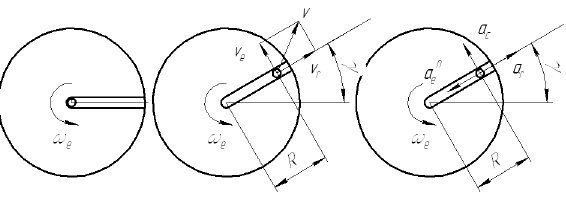
Определение положения точки
Определим, на какое расстояние переместится точка за время 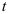
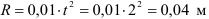
Определим, на какой угол повернется желоб за время
Если тело вращается равномерно, то за 1 сек тело повернется на 1 радиан (57,32°), тогда за 0,523 с тело повернется на 0,523 рад или 57,32 0,523 = 30°
Покажем на рисунке положение точки в момент времени t = 0,523 с.
Применяем теорему о сложении скоростей
Относительную скорость точки 
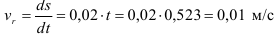
Переносная скорость точки 
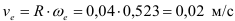
Так как 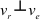
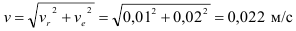
Применяем теорему о сложении ускорений
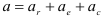
Относительное ускорение точки 
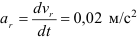
Переносное ускорение точки 
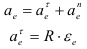
Так как тело движется с постоянной угловой скоростью 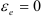
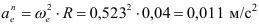
Ускорение Кориолиса:
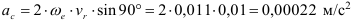
Абсолютное ускорение
Возможно эта страница вам будет полезна:
Основы теории механизмов и машин (понятии и определении)
Классификации кинематических пар
Теория механизмов и машин — научная дисциплина (или раздел науки), которая изучает строение (структуру), кинематику и динамику механизмов.
Механизмом называется система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемые движения других твердых тел
Типовыми механизмами будем называть простые механизмы, имеющие при различном функциональном назначении широкое применение в машинах/
Звено — твердое тело или система жестко связанных гел. входящих в состав механизма.
Стойка — звено, которое при исследовании механизма принимается за неподвижное.
Входное звено — звено, которому сообщается заданное движение и соответствующие силовые факторы (силы или моменты);
Выходное звено — то, на котором получают требуемое движение и силы.
Кинематическая цепь — система звеньев, образующих между собой кинематические пары.
Кинематическая пара — подвижное соединение двух звеньев, допускающее их определенное относительное движение.
Элементами кинематической пары называют совокупность поверхностей, линий или точек, по которым происходит подвижное соединение двух звеньев и которые образуют кинематическую пару.
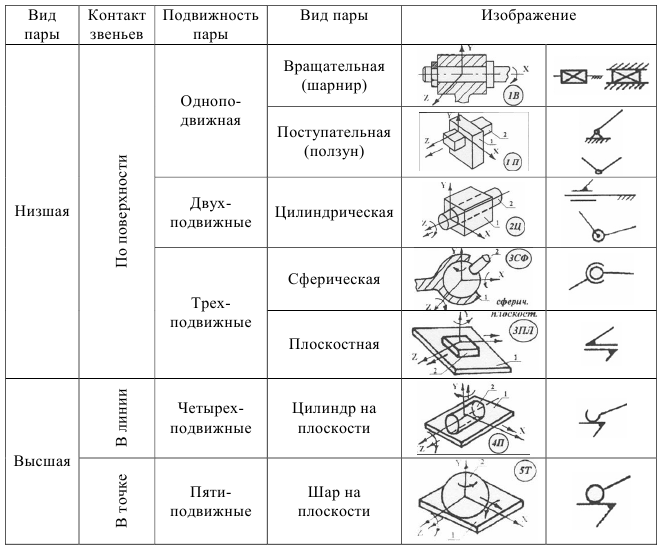
В зависимости от вида контакта элементов кинематических пар они делятся на высшие и низшие.
Кинематические пары, образованные элементами в виде линии или точки называются высшими.
Кинематические пары, образованные элементами в виде поверхностей, называются низшими.
В зависимости от степени подвижности они делятся на
- одноподвижные;
- двухподвижные;
- трехподвижные;
- четырех подвижные;
- пятнподвижные;
Рычажные механизмы. Основные виды рычажных механизмов
Рычажным называется механизм, звенья которого образуют только вращательные и поступательные пары.
Составляющие рычажных механизмов.
- Стойка — неподвижное звено, предназначенное для присоединения подвижных звеньев.
- Кривошип — звено совершающее полное вращательное движение вокруг неподвижной оси.
- Ползун — звено совершающее поступательное движение вдоль некоторой прямой.
- Коромысло — звено совершающее неполное вращательное движение вокруг неподвижной оси.
- Шатун — звено совершающее нлоскопараллельное движение и несвязанное со стойкой.
- Кулиса — звено совершающее вращательное либо сложное движение и образующее поступательную кинематическую пару с другим подвижным звеном — кулисным камнем.
- Кулисный камень — звено совершающее составное движение (поступательное кулисы в относительном движении, и вращательное вместе с кулисой в переносном движении).
Основные виды механизмов
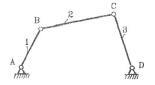
Кривошинно-шатунный механизм (Шарнирный чет ырехзвенник)
Состоит из кривошипа 1, шатуна 2, коромысла 3 и стойки, связанных между собой вращательными кинематическими парами
Кривошипно-ползунный механизм
Состоит из кривошипа 1, шатуна 2, ползуна 3 и стойки, связанных между собой вращательными кинематическими парами 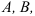
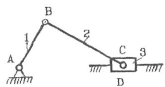
Кулисный механизм
Состоит из кривошипа 1, кулисного камня 2, кулисы 3 и стойки, связанных между собой вращательными кинематическими парами 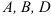
Структурный анализ механизмов
Структурный анализ механизма — это расчленение его на структурные группы. Структурные группы (группы Ассура) — это кинематические цепи, которые после присоединения к стойке имеют степень подвижности 
Степень подвижности механизма определяется по формуле Чебышева для рычажных механизмов.
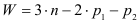
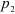
Структурную формулу любого простого или сложного механизма, образованного с помощью структурных групп, можно представить следующим образом:

За начальный механизм принимается ведущее звено со стойкой.
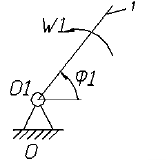
Все механизмы и структурные группы, в них входящие, делятся на классы, а класс-механизма в целом определяется высшим классом структурной группы, которая в него входит.
Элементарные механизмы условно отнесены к механизмам 1 класса.
Класс структурной группы определяется числом максимальным числом кинематических пар, на одном звене.
Порядок группы определяется числом внешних кинематических нар.
Виды структурных групп
Диада — структурная группа II класса, 2 порядка (И, 2) Состоит из двух звеньев и трех кинематических пар.
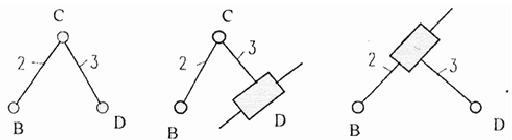
Трехповодок (Триада) — структурная группа III класса, 3 порядка (III, 3) Состоит из четырех звеньев и шести кинематических пар.
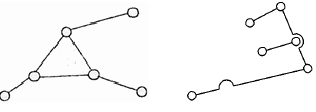
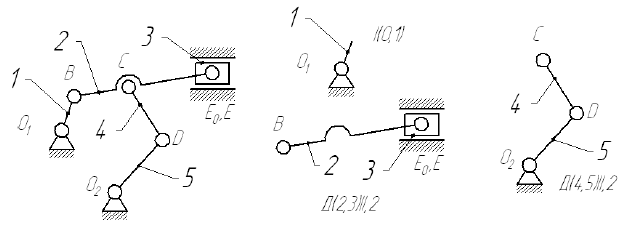
Порядок выполнения структурного анализа:
- Определение названья звеньев и кинематических пар.
- Определение степени подвижности механизма.
- Разложение механизма на структурные группы Асура.
- Определение класса и порядка всего механизма и построение формулы строения механизма.
Пример:

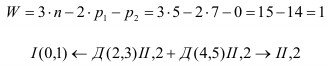
Пример:
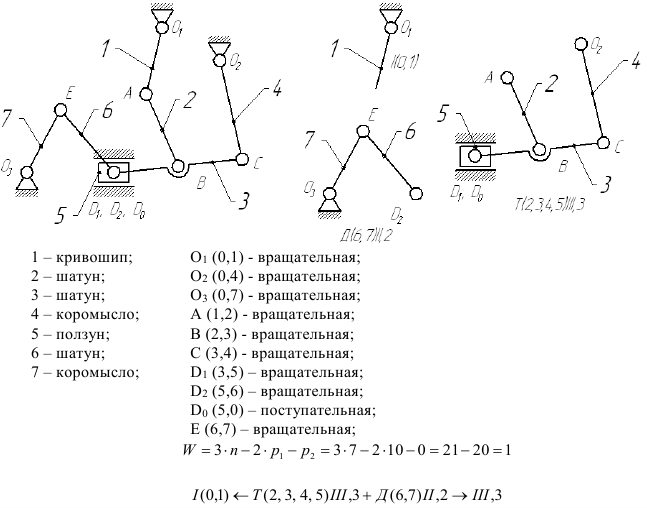
Возможно эта страница вам будет полезна:
Кулачковые механизмы
Кулачковые механизмы, подобно другим механизмам, служат для преобразования одного вида движения (на входе), в другой вид движения (на выходе) с одновременным преобразованием передаваемых силовых параметров (сил, моментов).
Основным преимуществом является возможность получения любого закона движения ведомого звена.
Кинематическая цепь простейшего кулачкового механизма состоит из двух подвижных звеньев (кулачка и толкателя), образующих высшую кинематическую пару, и стойки, с которой каждое из этих звеньев входит в низшую кинематическую пару.
Ведущим звеном механизма обычно является кулачок, который в большинстве случаев совершает непрерывное вращательное движение.
Ведомое звено, называемое толкателем, совершает возвратно-прямолинейное и возвратно-вращательное движение относительно стойки.
Классификация кулачковых механизмов
По виду выходного звена
- с толкателем
- с колебателем
По виду толкателя
- игольчатый
- роликовый
- плоский
По расположению толкателя
- центральный
- дезаксиальный
Основные параметры кулачка
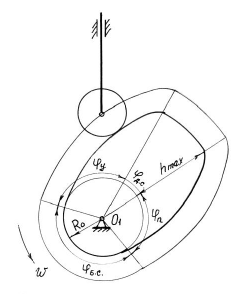
Профиль кулачка — это профиль, образованный центром ролика обеспечивающий заданный закон движения ведомого звена.
Минимальный радиус кулачка 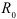
Максимальный радиус кулачка 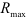
Максимальный подъем толкателя — расстояние между минимальным и максимальным радиусами кулачка 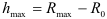
За один оборот кулачка происходит последовательное удаление толкателя от центра вращения кулачка, затем остановка и приближение к центру кулачка, вновь остановка и повторение всего цикла движения. Эти четыре этапа в движении кулачкового механизма называются фазами движения, которые ограничены соответствующими углами, называемыми фазовыми углами.
Фаза удаления 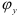
Фаза дальнего стояния 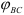
Фаза возврата 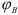
Фаза ближнего стояния 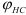
В некоторых кулачковых механизмах фазы ближнего и дальнего стояния могут отсутствовать, сразу обе или одна.
Рабочий угол кулачка — угол кулачка равный сумме углов удаления, дальнего стояния и возврата.
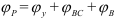
Угол давления — угол 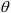
Зубчатые механизмы
Принцип действия и классификации. Основные параметры, геометрии и кинематика прямозубых колёс.
Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес.
Классификация:
По расположению осей валов:
- передачи с параллельными осями;
- передачи с пересекающимися осями;
- передачи с перекрещивающимися осями. По расположению зубьев на колесах:
- прямозубые
- косозубые.
По форме профиля зуба:
- эвольвентные
- круговые.
Основные параметры:
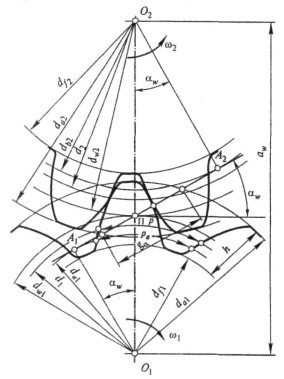
Ведущее зубчатое колесо называют шестерней, а ведомое — колесом. Параметрам шестерни приписывают индекс 1, а параметрам колеса — 2.
Геометрические параметры: 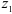
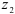
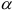
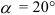
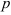
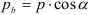
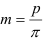
Модули стандартизованы (ГОСТ 9563-80) в диапазоне 0,05… 100 мм
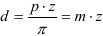
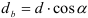
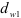
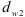
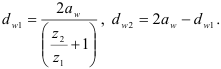
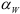
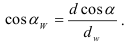
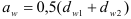
При нарезании колес со смещением делительная плоскость рейки смещается к центру или от центра заготовки на 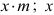
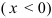
У передач без смещения и при суммарном смещении 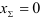
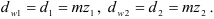
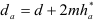
где 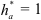
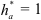
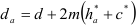
где 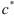
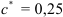
Передаточное отношение 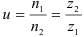
Виды зубчатых механизмов
Зубчатый механизм, составленный из зубчатых колес с неподвижными осями, называется зубчатым рядом.
Зубчатый ряд, состоящий из двух колес стойки, есть рядовая передача.
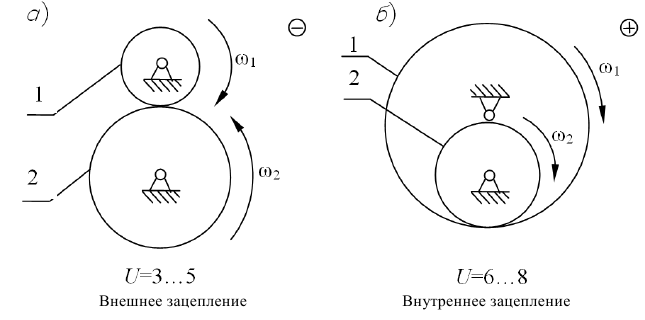
Значение передаточного отношения рядовой передачи обратно пропорционально числу зубьев колес:
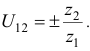
Знак перед дробью позволяет учесть направление вращения колес. Для внешнего зацепления принят знак (-), учитывающий противоположность вращения колес. Для внутреннего зацепления принят знак (+).
Передаточное отношение любого зубчатого ряда равно произведению передаточных отношений всех передач, входящих в него:
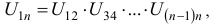
где 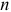
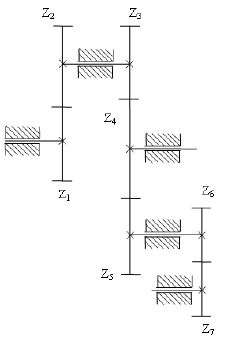
Определить передаточное отношение 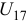
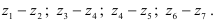
Общее передаточное отношение механизма равно:
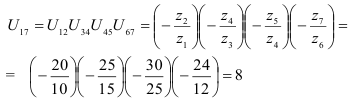
Колесо 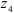
Зубчатый механизм, в состав которого входят зубчатые колеса с геометрически подвижной осью называются планетарным механизмом. В состав планетарного механизма входят звенья: Сателлиты — зубчатые колеса с геометрически подвижной осью;
Водило — подвижное звено, в котором помещена ось сателлита;
Солнечное колесо — подвижное центральное зубчатое колесо; Опорное колесо (эпицикл) — неподвижное центральное зубчатое колесо;
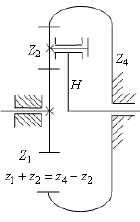
Геометрическая ось центральных колес и водила общая. Для обеспечения этого используют условие соосности
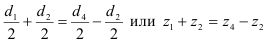
Определение передаточного отношении планетарной передачи
При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса.
Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило, как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от 
Для исследуемого механизма:
Для обращенного механизма:
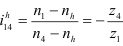
В нашем случае 4 заторможено, 1 — ведущее и 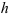
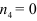
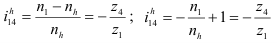
или
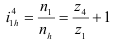
Основы материаловедения
Материалы, применяемые дли изготовления механизмов и машин.
Основным машиностроительным материалом является сплав железа и углерода, называемый чугуном или сталью в зависимости от процентного содержания углерода в сплаве.
Чугун содержит углерода свыше 2%. Различают:
Серый чугун (основной материал для литых деталей)
Маркировка: СЧ и цифры, соответствующие пределу прочности при растяжении (СЧ15- 150 МПа, СЧ20 — 200 МПа)
Свойства: жесткость, сравнительно малая прочность, хрупкость, хорошие литейные свойства,относительная дешевизна.
Высокопрочный чугун (чугун с повышенной прочностью).
Маркировка: ВЧ и цифры, соответствующие пределу прочности при растяжении (ВЧ40, ВЧ35)
Ковкий чугун (чугун с повышенным коэффициентом относительного удлинения)
Маркировка: КЧ 30-6, где 30 — предел прочности, 300 МПА; 6 — относительное удлинение, %.
Белый и отбеленный чугуны (не применяется).
Сталь — сплав железа с углеродом с содержанием углерода менее 1,6 %.
Сталь общего назначения (применяется для сварных соединений и в неответственных деталях)
Маркировка: ст 3, ст 5 (цифра обозначает условный номер марки в зависимости от химического состава)
Сталь качественная конструкционная (применяется для изготовления валов, стаканов, и.т.д.)
Маркировка: сталь 25, сталь 45 и т.п. Здесь цифры указывают содержание углерода в сотых долях процента.
Легированные стали (применяется для изготовления ответственных деталей зубчатых колес, червяков, цепей и.т.д) — это качественная конструкционная сталь с легирующими добавками, которые существенно улучшают свойства стали. В качестве легирующих добавок-чаще всего используют никель, хром, марганец и другие металлы.
Маркировка: сталь 40Х, сталь 40ХН, сталь 40 Х2Н. (здесь буквами X и Н обозначены хром и никель в количестве до 1%).
Сплавы на основе цветных металлов (применяются для изготовления венцов червячных колес, вкладышей подшипников скольжения и.т.д):
Сплав на основе меди:
- латунь — сплав медь-цинк;
- бронза — сплав медь-олово, медь-свинец, медь-алюминий.
- баббиты — сплавы на основе олова, свинца — баббиты.
Алюминиевые сплавы (используются для изготовления неответственных литых штампованных деталей ):
- силумины (сплавы с кремнием) — хорошо льются.
Маркировка: АЛ2, АЛ4 и т.п;
- дюралюмины (сплавы с медью и/или марганцем) — это деформируемые сплавы. Маркировка: Д1, Д16 и др.,
Основные механические характеристики материалов
Основные механические характеристики материала определяются при испытании образцов материала.
Рассмотрим цилиндр, находящийся под действием растягивающей силы 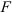
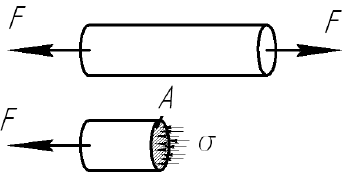
Под действием силы 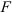
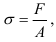
где 
Постепенно будем увеличивать нагрузку 
Для большинства материалов зависимость между напряжениями и деформациями выглядит следующим образом
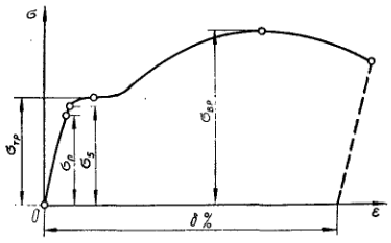
Данная зависимость имеет следующие характерные точки:
Предел пропорциональности 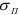
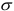
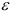
Предел упругости 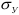
Предел текучести 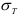
Предел прочности 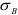
К основным характеристикам материалов также относятся:
- Модуль упругости
— отношение нормального напряжения
(в пределах
) к соответствующей относительной продольной деформации
.
- Твердость — свойство материала сопротивляться внедрению в него другого, более твердого гела.
- Для измерения твёрдости существует несколько шкал (методов измерения):
- Метод Бринелли — твёрдость определяется по диаметру отпечатка, оставляемому металлическим шариком, вдавливаемым в поверхность. Твёрдость, определённая по этому методу, обозначается
.
- Метод Роквелла — твёрдость определяется по относительной глубине вдавливания алмазного конуса в поверхность тестируемого материала. Твёрдость, определённая по этому методу обозначается
.
- Метод Виккерса — твёрдость определяется по площади отпечатка, оставляемого четырёхгранной алмазной пирамидкой, вдавливаемой в поверхность. Твёрдость, определённая по этому методу, обозначается
.
Основы сопротивлении материалов
Геометрические характеристики сечений
Детали механизмов и машин отличаются друг от друга по форме и размерам. При расчета на прочность деталей механизмов и машин используются поперечные сечения деталей, имеющие свои геометричекие характеристики.
Рассмотрим геометричекие характеристики плоских сечений.
Площадь —
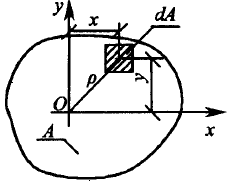
Статический момент относительно оси 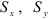
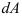
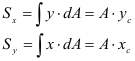
где 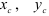
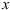
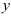
Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:
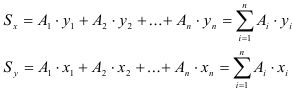
где 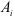
Последнее выражение позволяет определить положение центра тяжести для любого составного сечения
Пример:
Определить положение центра тяжести сечения показанного на рисунке.
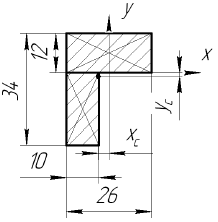
Проводим оси 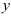
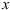
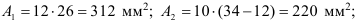
Находим расстояние от центров тяжестей фигур до осей
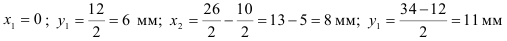
Записываем выражение для статических моментов инерции
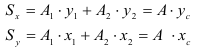
Отсюда
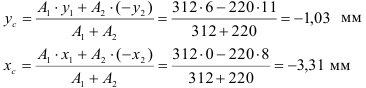
Осевой момент инерции относительно оси сумма произведений площадей элементарных площадок 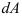
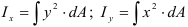
Полярный момент инерции плоского сечения относительно некоторой точки (полюса) 
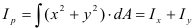
Пример:
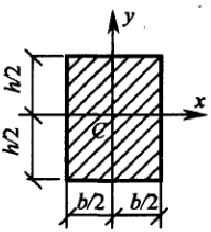
Определить осевые и полярный моменты инерции прямоугольника высотой 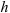
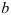
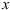
Представим 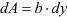
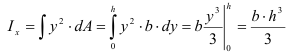
Представим 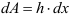
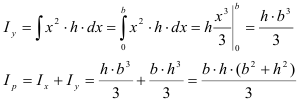
Осевой момент сопротивления относительно оси — отношение осевого момента инерции к расстоянию от наиболее удаленной точки сечения по этой оси
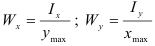
Полярный момент сопротивления относительно точки (полюса) — отношение полярного момента инерции к расстоянию от наиболее удаленной точки сечения до полюса
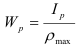
Пример:
Для предыдущего примера определить осевые и полярные моменты сопротивления
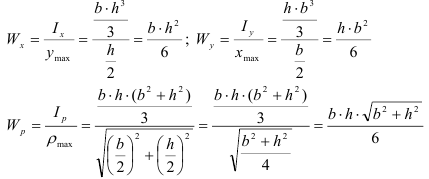
Для основных сечений формулы для расчета геометрических характеристик приводятся в технических справочниках.
Виды нагружения
Растяжение-сжатие
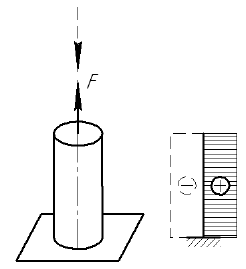
При воздействии на тело силы, линия действия которой проходит по оси данного тела, в поперечном сечении (перпендикулярном линии действия силы) возникают напряжения, называемые напряжениями растяжения или сжатия, в зависимости от направления действия силы.
В случае растяжения-сжатия прочность тела оценивается но формуле
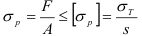
где 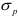
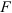
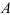
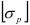
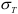
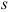
Для удобства представления информации на расчетной схеме напряжения представляются в виде эпюр.
Эпюра — группа условных линий, показывающих величину и направление напряжений, возникающих в рассматриваемом теле.
Если по длине тела изменяются размеры поперечного сечения или приложенная нагрузка, то изменятся и величина напряжений
Пример:
Построить эпюры напряжений для бруса, изображенного на рисунке.
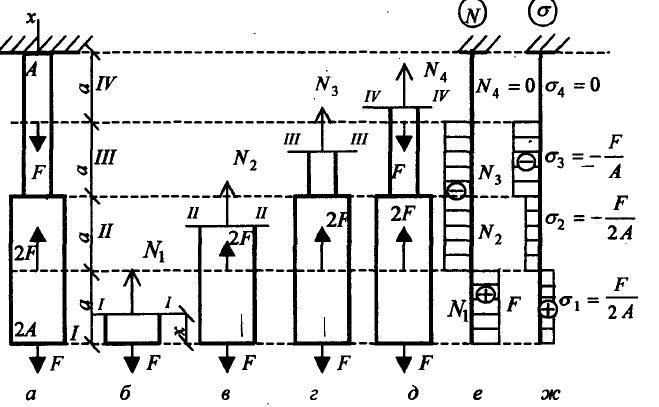
Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил.
Проводим сечение I-I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 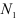
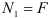
Определим напряжения на участке I:
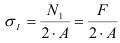
Проводим сечение II—II. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 
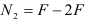
Определим напряжения на участке II:
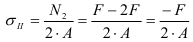
Проводим сечение III—III. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 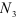
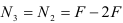
Определим напряжения на участке III:
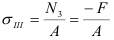
Проводим сечение IV-IV. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 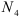
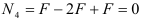
Определим напряжения на участке IV:
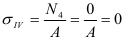
Срез (сдвиг) и смятие
Срезом называют деформацию, представляющую собой смещение поперечных плоскостей тела под действием силы параллельной этой плоскости.
Касательные напряжения при срезе (напряжения среза) определяются по формуле
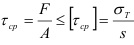
где 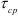
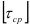
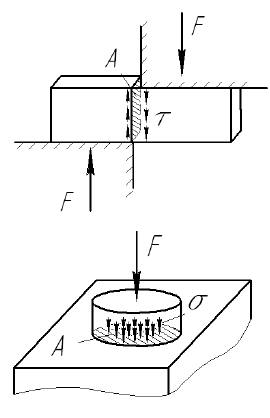
Смятием называют деформацию, представляющую собой нарушение первоначальной формы поверхности под действием силы перпендикулярной к этой поверхности.
Нормальные напряжения при смятии (напряжения смятия) определяются по формуле
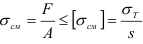
Пример
Определить напряжения среза и смятия для заклепки соединяющей три детали. Известны диаметр заклепки 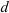
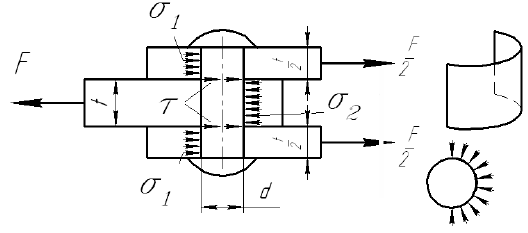
Запишем условие прочности на срез для заклепки
В соединении 3-х деталей напряжения среза возникают в двух сечениях круглой формы.
Площадь круга 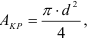
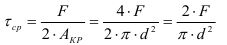
Запишем условие прочности на смятие для заклепки
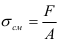
В соединении 3-х деталей напряжения смятия возникают на боковых поверхностях заклепки площадь которых будет определяться:
Для верхней и нижней поверхностей:
Для средней поверхности:
Тогда напряжения смятия
Для верхней и нижней поверхностей:
Для средней поверхности:
Возможно эта страница вам будет полезна:
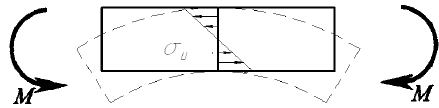
Изгиб
Изгиб представляет собой такую деформацию, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Изгиб называют чистым если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении бруса (балки).
Изгиб называют поперечным, если в поперечных сечениях бруса наряду с изгибающими моментами возникают также и поперечные силы.
При изгибе в сечении деталей возникают нормальные напряжения 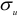
Напряжения изгиба определяются по формуле
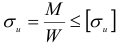
На практике изгиб тела вызывает не только внешние изгибающие моменты, но и поперечные силы, действующие на тело. Для нахождения наиболее нагруженного поперечного сечения строят эпюры изгибающих моментов.
При построении эпюр изгибающих моментов используются следующие правила:
- Тело разбивается на участки, границами которых служат точки приложения внешних сил и моментов и реакции опор;
- Построение ведется последовательно, по участкам, путем проведения сечений, проходящих через середину участка и отбрасывания части тела лежащей за сечением. Для неотброшенной части тела составляется зависимость по которой изменяется изгибающий момент и определяется его значение в начале и конце участка;
- Построение эпюры ведется о стороны растянутых волокон;
- Если в рассматриваемом сечении приложен внешний момент, то на эпюре наблюдается скачек на величину этого момента.
Построение эпюр изгибающих моментов рассмотрим на примере.
Пример:
Проверить на прочность балку постоянного сечения, показанную на рисунке, если известно, что осевой момент сопротивления ее сечения 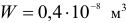
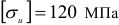
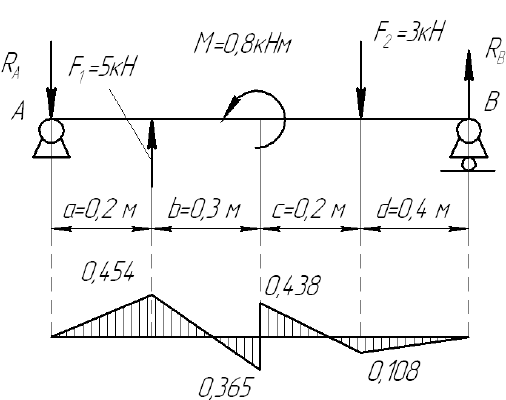
1 Определяем реакции опор
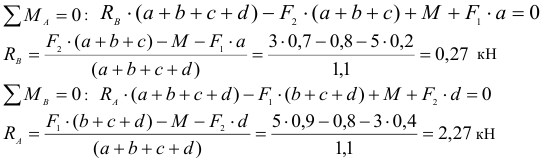
Проверка
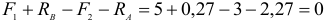
2 Разбиваем эпюру на участки
Участок 1
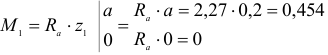
Участок 2
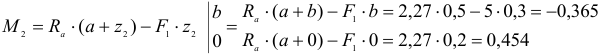
Участок 3
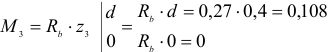
Участок 4
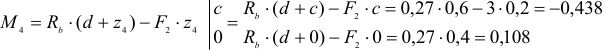
Проверка
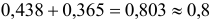
Наибольший момент
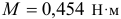
Определяем напряжение изгиба
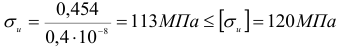
Кручение
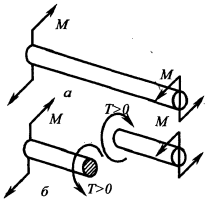
Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси. Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
При кручении в сечении деталей возникают касательные напряжения 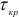
Напряжения кручения определяются по формуле
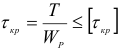
Если вал нагружен несколькими крутящими моментами, то для нахождения наиболее нагруженного поперечного сечения строят эпюры крутящих моментов.
При построении эпюр кругящих моментов принимают следующее правило знаков: если при взгляде в торец отсеченной части вала действующий в этом сечении момент оказывается направленным против хода часовой стрелки, то он считается положительным, а если по ходу часовой стрелки — отрицательным.
Пример:
На валу установлено 4 диска, к которым подвешены грузы.
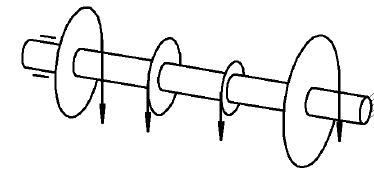
Проверить на прочность вал показанный на рисунке. Известен диаметр вала 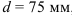
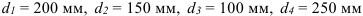
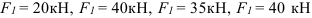
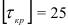
Определим крутящие моменты на валах
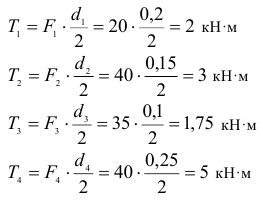
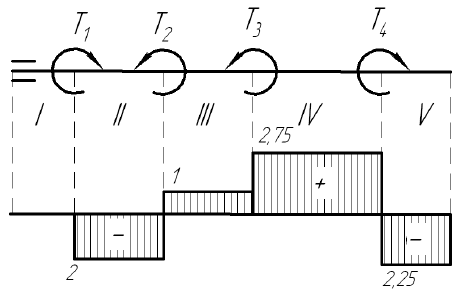
Строим расчетную схему и эпюру крутящих моментов Разбиваем вал на участки
Рассматриваем участок I: Проводим сечение I-I и отсекаем правую часть
Рассматриваем участок II: Проводим сечение 11-11 и отсекаем правую часть
Рассматриваем участок III: Проводим сечение III-I1I и отсекаем правую часть
Рассматриваем участок IV: Проводим сечение IV — IV и отсекаем правую часть
Рассматриваем участок V: Проводим сечение V — V и отсекаем правую часть
По эпюре определяем наибольший момент
Записываем условие прочности
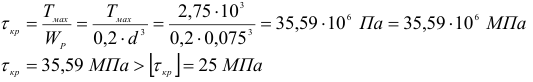
Контактные напряжении
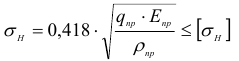
где 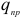
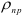
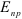
Удельная нагрузка
Приведенный радиус кривизны:
где 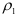
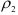
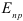
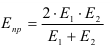
Основные параметры механической передачи
Механической передачей называют механизм, который преобразует параметры движения двигателя в процессе передачи его от двигателя к исполнительным органам машины.
Все механические передачи разделяют на две основные группы:
- передачи, основанные на использовании трения (ременные, фрикционные);
- передачи, основанные на использовании зацепления (зубчатые, червячные, цепные, винтовые).
Передачи выполняют с постоянным или переменным (регулируемым) передаточным отношением.
Регулирование передаточного отношения может быть ступенчатым или бесступенчатым:
- ступенчатое регулирование выполняют в коробках скоростей с зубчатыми колесами, в ременных передачах со ступенчатыми шкивами и г. п.;
- бесступенчатое регулирование — с помощью фрикционных или цепных вариаторов.
Основные параметры передач:
- В каждой передаче различают два основных вала: входной и выходной, или ведущий и ведомый. Между этими валами в многоступенчатых передачах располагаются промежуточные валы.
Основные характеристики передач:
Эти характеристики минимально необходимы и достаточны для проведения проектного расчета любой передачи.
Кроме основных, различают производные характеристики:
- коэффициент полезного действия (КПД)
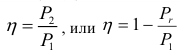
где 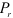
- передаточное отношение, определяемое в направлении потока мощности,
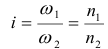
Производные характеристики часто используют взамен основных. Например, передачу можно определять с помощью 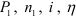
При 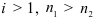
При 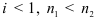
Наибольшее распространение имеют понижающие передачи, так как частота вращения исполнительного механизма в большинстве случаев меньше частоты вращения двигателя.
При расчете передач часто используют следующие зависимости между различными параметрами:
-выражение мощности 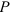
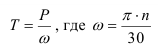
Зубчатые передачи
Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес. Кла с си фика ция:
По расположению осей валов различают:
- передачи с параллельными осями, которые выполняют с цилиндрическими колесами внешнего или внутреннего зацепления;

- передачи с пересекающимися осями — конические колеса;
- передачи с перекрещивающимися осями — цилиндрические винтовые, конические гипоидные.
- передачи между зубчатым колесом и рейкой.

По расположению зубьев на колесах различают передачи:
- прямозубые
- косозубые.
По форме профиля зуба различают эвольвентные и круговые.
Основные преимущества зубчатых передач:
- высокая нагрузочная способность и, как следствие, малые габариты;
- большая долговечность и надежность работы;
- высокий КПД. (до 0,97…0,98 в одной ступени);
- постоянство передаточного отношения;
-возможность применения в широком диапазоне скоростей (до 150 м/с), мощностей (до десятков тысяч кВт) и передаточных отношений (до нескольких сотен и даже тысяч). Основные недостатки:
- повышенные требования к точности изготовления;
- шум при больших скоростях;
- высокая жесткость, не позволяющая компенсировать динамические нагрузки.
Червячные передачи
Передача состоит из червяка и червячного колеса
Червячная передача относится к передачам зацепления с 4 перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Возможны и другие углы, отличные от 90°, однако такие передачи применяют редко.
Движение в червячных передачах преобразуется по принципу винтовой пары или по принципу наклонной плоскости.
Основные преимущества червячной передачи: возможность получения больших передаточных отношений в одной паре; плавность и бесшумность работы; повышенная кинематичекая точность; возможность самоторможения (при низком КПД).
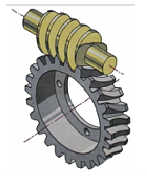
Недостатки этой передачи: сравнительно низкий КПД; повышенный износ и склонность к заеданию; необходимость применения для колес дорогих антифрикционных материалов (бронза); повышенные требования к точности сборки (точное aw, расположение оси червяка в средней плоскости колеса).
Червячные передачи дороже и сложнее зубчатых, поэтому их применяют при необходимости передачи движения между перекрещивающимися валами, а также в механизмах, где необходимы большие передаточные отношения и высокая кинематическая точность, например делительные устройства, механизмы наведения и т. п. Червячные передачи применяют в подъемно-транспортных машинах, станкостроении, автомобилестроении и др.
Ременные и ценные передачи
Ременная передача состоит из двух шкивов, закрепленных на валах, и ремня, охватывающего шкивы. Нагрузка передается силами трения, возникающими между шкивами и ремнем вследствие натяжения последнего.
В зависимости от формы поперечного сечения ремня различают:
плоскоременную, клиноременную и кругло-ременную передачи.
Оценка и применение
Основные преимущества ременной передачи:
- возможность передачи движения на значительное расстояние (до 15 м и более);
- плавность и бесшумность работы, обусловленные эластичностью ремня и позволяющие работать при высоких скоростях
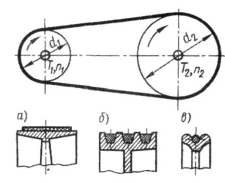
- предохранение механизмов от резких колебаний нагрузки вследствие упругости ремня;
- предохранение механизмов от перегрузки за счет возможного проскальзывания ремня;
- простота конструкции и эксплуатации (передача не требует смазки).
Основными недостатками ременной передачи являются:
- повышенные габариты;
- некоторое непостоянство передаточного отношения, вызванное зависимостью скольжения ремня от нагрузки;
- повышенная нагрузка на валы и их опоры, связанная с большим предварительным натяжением ремня (увеличение нагрузки на валы в 2…3 раза по сравнению с зубчатой передачей);
- низкая долговечность ремней (в пределах от 1000 до 5000 ч).
Ременные передачи применяют преимущественно в тех случаях, когда по условиям конструкции валы расположены на значительных расстояниях. Мощность современных передач не превышает обычно 50 кВт. В комбинации с зубчатой передачей ременную передачу устанавливают обычно на быстроходную ступень, как менее нагруженную.
В современном машиностроении наибольшее распространение имеют клиновые ремни. Применение плоских ремней старой конструкции значительно сократилось. Плоские ремни новой конструкции (пленочные ремни из пластмасс) получают распространение в высокоскоростных передачах. Круглые ремни применяют только для малых мощностей: в приборах, машинах домашнего обихода и т. п.
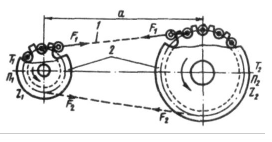
епная передача с основана на зацеплении цепи 1 и звездочек 2.
Зубчатые цепи классифицируются:
По виду приводных цепей:
- роликовые;
- втулочные;
- зубчатые цепи.
По числу рядов цепей:
- однорядные;
- многорядные.
По виду применяемых шарниров:
- шарниры скольжения;
- шарниры качения.
Преимущества передачи перед ременными:
- возможность передавать цепью при прочих равных условиях большие нагрузки;
- отсутствие скольжения и буксования;
- постоянство передаточного отношения;
- возможность работы при значительных кратковременных перегрузках;
- не требуется предварительного натяжения цепи, в связи с чем уменьшается нагрузка на валы и опоры;
- возможность передачи мощности от одного ведущего вала нескольким ведомым. Недостатки: Основной причиной этих недостатков является то, что цепь состоит из отдельных жестких звеньев и располагается на звездочке не по окружности, а по многоугольнику. С этим связаны износ шарниров цепи, шум и дополнительные динамические нагрузки, необходимость организации системы смазки.
Цепные передачи применяют при значительных межосевых расстояниях, а также для передачи движения от одного ведущего вала нескольким ведомым в тех случаях, когда зубчатые передачи неприменимы, а ременные недостаточно надежны.
Фрикционные передачи
Принцип действии и классификации.
Работа фрикционной передачи основана на использовании сил трения, которые возникают в месте контакта двух тел вращения под действием сил прижатия 
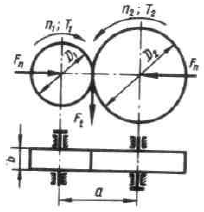
где 
Для передачи с цилиндрическими катками
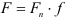
где 
Нарушение этого условия приводит к буксованию и быстрому износу катков.
Классификации передач
По возможности регулирования передаточного отношения:
- передачи нерегулируемые, т. е. с постоянным передаточным отношением;
- передачи регулируемые (вариаторы), позволяющие изменять передаточное отношение.
По форме поверхности рабочих катков:
- с цилиндрической;
- с конической;
- с шаровой;
- сторовой.
По расположению валов:
- с параллельными валами;
- с пересекающимися валами.
Область применении
Фрикционные передачи с постоянным передаточным отношением применяют сравнительно редко. Их область ограничивается преимущественно кинематическими цепями приборов, от которых требуются плавность движения, бесшумность работы, безударное включение на ходу и т. п. Как силовые (не кинематические) передачи, они не могут конкурировать с зубчатыми передачами по габаритам, надежности, КПД и пр.
Фрикционные вариаторы применяют как в кинематических, так и силовых передачах в тех случаях, когда требуется бесступенчатое регулирование скорости (зубчатая передача не позволяет такого регулирования). Применение фрикционных вариаторов на практике ограничивается диапазоном малых и средних мощностей — до 10 реже до 20 кВт. В этом диапазоне они успешно конкурируют с гидравлическими и электрическими вариаторами, отличаясь от них простотой конструкции, малыми габаритами и повышенным КПД. При больших мощностях трудно обеспечивать необходимую силу прижатия катков. Эта сила, а также соответствующие нагрузки на валы и опоры становятся слишком большими, конструкция вариатора и нажимного устройства усложняется.
Фрикционные вариаторы нашли применение в станкостроении, сварочных и литейных машинах, машинах текстильной, химической и бумажной промышленности, различных отраслях приборостроения и т. д.
Фрикционные передачи любого типа неприменимы в конструкциях, от которых требуется жесткая кинематическая связь, не допускающая проскальзывания или накопления ошибок взаимного положения валов.
Передача «Винт-гайка»
Передача винт — гайка служит для преобразования вращательного движения в поступательное.
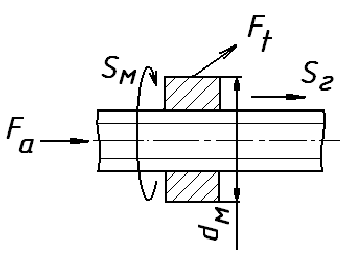
В винтовых механизмах вращение винта или гайки осуществляют обычно с помощью маховика, шестерни и т. п. При этом передаточное отношение условно можно выразить отношением окружного перемещения маховичка 
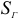
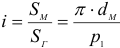
где 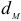
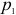
При малом 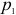
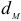
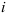
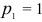
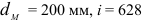
Зависимость между окружной силой 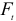
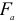
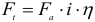
где 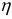
При простой и компактной конструкции передачи винт — гайка позволяет получить большой выигрыш в силе или осуществлять медленные и точные перемещения.
Основной недостаток передачи — низкий КПД.
Соединения
Неподвижные связи в технике называют соединениями.
По признаку разъемности все виды соединений можно разделить на разъемные и неразъемные.
Разъемные соединения позволяют разъединять детали без их повреждения. К ним относятся резьбовые, штифтовые, клеммовые, шпоночные, шлицевые и профильные соединения.
Неразъемные соединения не позволяют разъединять детали без их повреждения. Применение неразъемных соединений обусловлено в основном технологическими и экономическими требованиями. К этой группе соединений относятся заклепочные, сварные и соединения с натягом.
Сварные соединении
Сварка — это соединение деталей за счет их расплавления в зоне стыка маховичка.
Виды сварки
- кузнечная (соединение деталей нагретых до высокой температуры иод действием ударных нагрузок );
- луговая металлическим электродом (расплавление металла в зоне их стыка за счет электрической дуги);
- контактная (расплавление деталей за счет пропускания тока и выделения при этой большого количества теплоты в зоне их стыка);
Виды сварных соединений
Стыковое соединение — соединение деталей, при котором они прилегают друг к другу торцами.
Соединение выполняется стыковыми сварными швами, при которых расплавление металла осуществляется на всю глубину торца.
В зависимости or толщины деталей соединение может выполняться без разделки кромок или с разделкой кромок
Нахлесточное соединение — соединение деталей, при котором они прилегают друг к другу широкими гранями.
Соединение выполняется угловыми сварными швами
Основными геометрическими характеристиками поперечного сечения нормального углового шва катет 
В зависимости от формы поперечного сечения различают угловые швы:
В зависимости от расположения различают швы лобовые, фланговые Лобовой шов расположен перпендикулярно, а фланговый — параллельно линии действия нагружающей силы. Обычно применяют комбинированное соединение фланговыми и лобовыми швами.

Тавровое соединение. Соединяемые детали в зоне сварных швов перпендикулярны (наиболее частый случай) или наклонны друг к другу. Это соединение выполняют стыковым швом с разделкой кромок или угловыми швами без разделки кромок. При нагружении изгибающим моментом и силой прочность соединения определяют по формулам:
Резьбовые соединении
Классификация резьб:
Резьба — выступы, образованные на основной поверхности винтов или гаек и расположенные по винтовой линии.
По форме основной поверхности различают цилиндрические и конические резьбы. По направлению винтовой линии различают правую и левую резьбы. По числу заходов различают однозаходную, двухзаходную и т. д. резьбы. По форме профиля:
- метрическая с треугольным профилем — основная крепежная резьба; трубная — треугольная со скругленными вершинами и впадинами; круглая; резьба винтов для дерева; прямоугольная; трапецеидальная симметричная; упорная.
Классификация соединений
Соединение болтом или винтом с гайкой — болтовое соединение Соединение болтом или винтом, завернутым в резьбовое отверстие — винтовое соединение
Соединение шпилькой
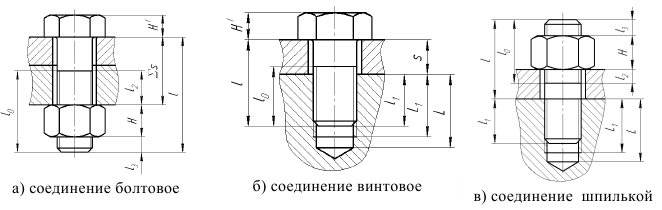
Детали, образующие резьбовые соединения
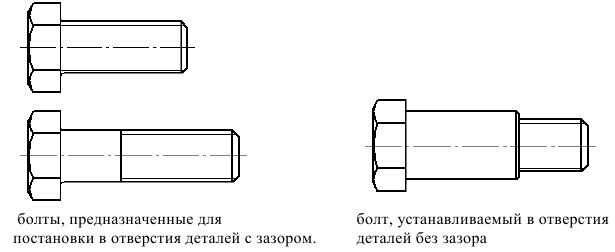
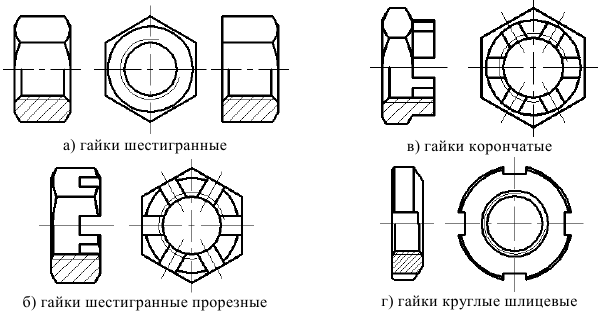
Болты
По форме стержня болты изготавливают для постановки в отверстие с зазором и без зазора.
Гайки различают по форме и по размерам:
Гайки шестигранные с нормальным и уменьшенным размером иод ключ, высокие и низкие.
Гайки прорезные и гайки корончатые с прорезью под шплинты. Применяются для стонорениясоединения
Гайки круглые с прорезями под ключ применяются, главным образом, для закрепления деталей на валах.
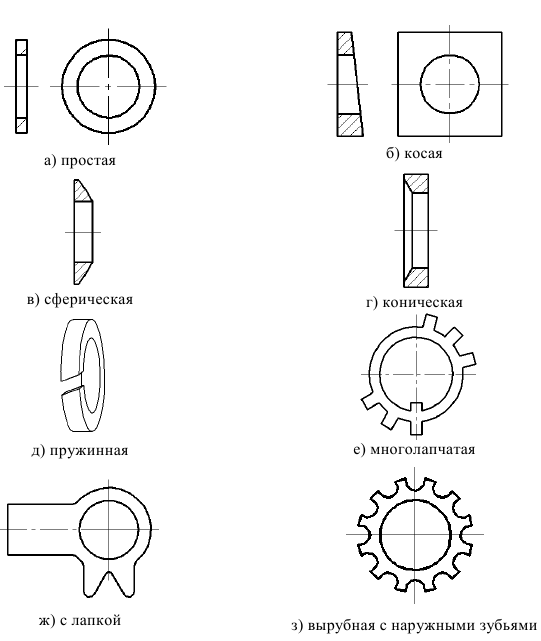
Шайбы
Все типы шайб можно разделить на две основные группы:
- а) шайбы подкладные;
- б) шайбы стопорные.
Шайба простая ставится под гайку или головку винта с целью предохранения, чистых поверхностей деталей от повреждения при завинчивании гайки (винта) и уменьшения смятия деталей гайкой, если деталь изготовлена из менее прочного материала.
Шайбы косые используются для устранения изгиба стержня болта при опоре гайки на полки прокатных профилей.
Шайба сферическая в комплекте с шайбой конической обеспечивают самоустановку гаек (головок болтов), и поэтому осевая нагрузка распределяется строго по оси стержня болта.
Шайбы пружинные применяют для стопорения гайки или головки винта относительно корпуса (предохранение резьбовых соединений от самоотвинчивания).
Шайбы стопорные многолапчатые служат для закрепления круглых гаек относительно вала. Внутренний выступ входит в паз на валу, один из наружных выступов загибается в шлиц гайки.
Шайбы стопорные с лапкой (применяют для закрепления гайки или головки винта относительно корпуса, путем, пластических деформаций: шайбу загибают на деталь и на грань гайки или головки винта.
Шайбы стопорные вырубные с внутренними зубьями
Соединение посадкой с натягом
Соединение двух деталей по круговой цилиндрической поверхности можно осуществить непосредственно без применения болтов, шпонок и т. д. Для этого достаточно при изготовлении деталей обеспечить натяг посадки, а при сборке запрессовать одну деталь в другую.
Натягом 
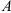
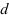
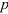
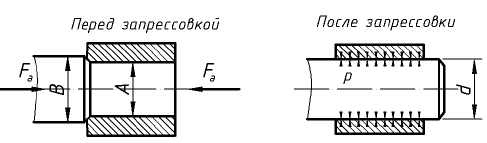
Нагрузочная способность соединения прежде всего зависит от натяга, величину которого устанавливают в соответствии с нагрузкой. Практически натяг очень невелик, он измеряется микрометрами и не может быть выполнен точно. Неизбежные погрешности производства приводят к рассеиванию натяга, а следовательно, и к рассеиванию нагрузочной способности соединения. Рассеивание натяга регламентируется стандартом допусков и посадок.
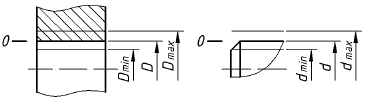
Основные понятия о натяге рассматриваются на примере сопряжения вал-втулка.
Различают размеры:
Допуск 
Допуск стандартизирован и обозначается латинскими буквами:
Посадка определяет характер сопряжения. Различают посадки с зазором, натягом и переходные. Обычно допуск отверстия принимают по 
Основные посадки на чертеже: 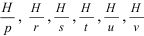
Способы сборки
Сборку соединения выполняют одним из трех способов: прессованием, нагревом втулки, охлаждением вала.
Прессование — распространенный и несложный способ сборки. Однако этому способу свойственны недостатки: смятие и частичное срезание (шабровка) шероховатостей посадочных поверхностей, возможность неравномерных деформаций деталей и повреждения их торцов. Шабровка и смятие шероховатостей приводят к ослаблению прочности соединения до полугора раз по сравнению со сборкой нагревом или охлаждением. Для облегчения сборки и уменьшения шабровки концу вала и краю отверстия рекомендуют придавать коническую форму (рис. 7.2).
Шабровка поверхностей контакта устраняется полностью при сборке по методу нагревания втулки (до 200…400°С) или охлаждения вала (твердая углекислота -79°С, жидкий воздух -196°С). Недостатком метода нагревания является возможность изменения структуры металла появление окалины и коробления. Метод охлаждения свободен от этих недостатков, однако требует наличия дорогого криогенного оборудования.
Шпоночные и шлицевые соединении
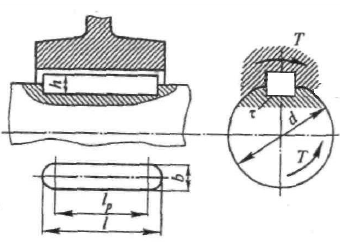
Шпоночные и зубчатые соединения служат для закрепления деталей на осях и валах. Такими деталями являются шкивы, зубчатые колеса, муфты, маховики, кулачки и т. д. Соединения нагружаются в основном вращающим моментом.
Для образования
шпоночного соединения на валу и в ступице выполняются пазы, в которые помещается специальная деталь, называемая шпонкой.
Момент передается с вала на ступицу боковыми узкими гранями шпонки. Шпонки стандартизированы. У стандартных шпонок ГОСТ 23360-78 размеры 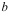
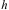
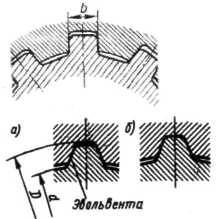
Зубчатые соединения образуются при наличии наружных зубьев на валу и внутренних зубьев в отверстии ступицы. Размеры зубчатых соединений, а также допуски на них стандартизованы.
Зубья на валах получают фрезерованием, строганием или накатыванием. Зубья в отверстиях образуют протягиванием или долблением.
По форме профиля различают зубья ирямобочные, эвольвентные и треугольные.
Треугольные зубчатые (шлицевые) соединения применяются главным образом для неподвижных соединений при передаче небольших крутящих моментов.
Профиль зуба в плоскости, перпендикулярной оси соединения — треугольник, биссектриса угла, при вершине которого проходит через центр сечения.
Чаще всего эти соединения используют с целью избежать прессовых посадок, применение которых но каким-либо причинам нежелательно, а также при
тонкостенных втулках. Соединения этого типа не стандартизованы.
Соединения с прямобочными зубьями являются наиболее часто применяемыми.
Соединения с эвольвентными зубьями
предпочтительны при больших диаметрах валов, когда для нарезания зубьев в отверстии и на валу могут быть использованы весьма совершенные технологические способы, применяемые для зубчатых колес.
Заклёпочные соединении
Образуются с помощью специальных деталей — заклёпок. Заклёпка имеет грибообразную форму и выпускается с одной головкой (закладной) вставляется в совместно просверленные детали, а затем хвостовик-ударами молотка или пресса расклёпывается, образуя вторую головку (замыкающую). При этом детали сильно сжимаются, образуя прочное, неподвижное неразъёмное соединение.
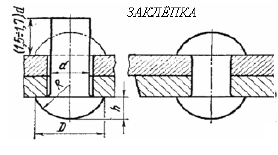
Достоинства заклёпочного соединения: + соединяют не свариваемые детали; + не дают температурных деформаций; + детали при разборке не разрушаются. Недостатки заклёпочного соединения: детали ослаблены отверстиями; высокий шум и ударные нагрузки при изготовлении; повышенный расход материала. Заклёпки изготавливают из сравнительно мягких материалов: Ст2, СтЗ, СтЮ, Ст15, латунь, медь, алюминий.
Заклёпки стандартизованы и выпускаются в разных модификациях.
Сплошные с полукруглой головкой (а) ГОСТ 10299-80, 14797-85 для силовых и плотных швов;
Сплошные с плоской головкой (б) ГОСТ 14801-85 для коррозионных сред;
Сплошные с потайной головкой (в) ГОСТ 10300-80, 14798-85 для уменьшения аэро- и гидросопротивления (самолёты, катера);
Полупустотелые (г,д,е) ГОСТ 12641-80, 12643-80 и пустотелые (ж,з,и) ГОСТ 12638-80, 12640-80 для соединения тонких листов и неметаллических деталей без больших нагрузок.
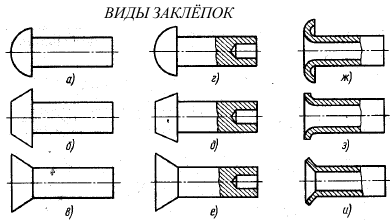
Общемашиностроительные детали
Классификация валов и осей
На валах и осях размещают вращающиеся детали: зубчатые колеса, шкивы, барабаны и т. п. Вал отличается от оси тем, что передает вращающий момент от одной детали к другой, а ось не передает. Вал всегда вращается, а ось может быть вращающейся или невращающейся.
Различают валы прямые, коленчатые и гибкие.
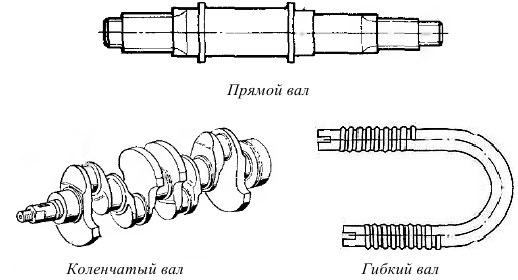
Наибольшее распространение имеют прямые валы.
Коленчатые валы применяют в поршневых машинах.
Гибкие валы допускают передачу вращения при больших перегибах (например, в зубоврачебных бормашинах).
Коленчатые и гибкие валы относят к специальным деталям и не изучают в настоящем курсе.
По конструкции различают валы и оси гладкие и фасонные или ступенчатые а также сплошные и полые.
Образование ступеней связано с закреплением деталей на валу или самого вала в осевом направлении, а также с возможностью монтажа детали при посадках с натягом. Полыми валы изготовляют для уменьшения массы или в тех случаях, когда через вал пропускают другую деталь, подводят масло и пр.
Прямые валы изготовляют преимущественно из углеродистых и легированных сталей. Чаще других применяют сталь Ст5 для валов без термообработки; сталь 45 или 40Х для валов с термообработкой (улучшение); сталь 20 или 20Х для быстроходных валов на подшипниках скольжения, у которых цапфы цементируют для повышения износостой кости.
Подшипники
Подшипники служат опорами для валов и вращающихся осей. Они воспринимают радиальные и осевые нагрузки, приложенные к валу, и сохраняют заданное положение оси вращения вала. Во избежание снижения КПД механизма потери в подшипниках должны быть минимальными.
Подшипники классифицируют по виду трения и воспринимаемой нагрузке.
По виду трения различают:
- подшипники скольжения
- подшипники качения.
По воспринимаемой нагрузке различают подшипники: радиальные — воспринимают радиальные нагрузки; упорные — воспринимают осевые нагрузки;
радиально-упорные и упорно-радиальные — воспринимают радиальные и осевые нагрузки.
Подшипники скольжения
Опорный участок вала называют цапфой. Форма рабочей поверхности подшипника скольжения, так же как и форма цапфы вала, может быть
- цилиндрической;
- плоской;
- конической;
- шаровой;
Цапфу, передающую радиальную нагрузку, называют: шипом, если она расположена на конце вала шейкой при расположении в середине вала.
Цапфу, передающую осевую нагрузку, называют пятой, а опору (подшипника) — подпятником.
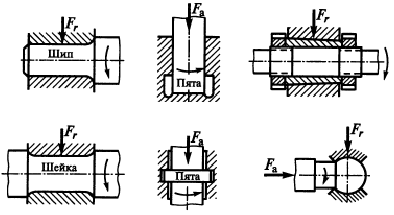
Подпятники работают обычно в паре с радиальными подшипниками. Большинство радиальных подшипников могут воспринимать также и небольшие осевые нагрузки (фиксируют вал в осевом направлении). Для этого вал изготовляют ступенчатым с галтелями, а кромки подшипника закругляют.
Основным элементом в подшипнике является вкладыш с тонким слоем антифрикционного материала на опорной поверхности. Вкладыш устанавливают в специальном корпусе подшипника 2 или непосредственно в корпусе машины.
Область применения подшипников скольжения:
- разъемные подшипники, необходимые по условиям сборки, например для коленчатых валов;
- высокоскоростные подшипники
, в условиях работы которых долговечность подшипников качения резко сокращается (вибрации, шум, большие инерционные нагрузки на тела качения);
- подшипники прецизионных машин, от которых требуется особо точное направление валов и возможность регулировки зазоров;
- подшипники, работающие в особых условиях (воде, агрессивных средах и т. п.), в которых подшипники качения неработоспособны из-за коррозии;
- подшипники дешевых тихоходных механизмов и некоторые другие.
Подшипники качения
Преимущества:
- меньше зависят от смазки
- упрощаются система смазки и обслуживания подшипника
- уменьшается возможность разрушения при кратковременных перебоях в смазке
- конструкция подшипников качения позволяет изготовлять их в массовых количествах как стандартную продукцию, что значительно снижает стоимость производства.
Недостатки:
- отсутствие разъемных конструкций
- сравнительно большие радиальные габариты
- ограниченная быстроходность
- низкую работоспособность при вибрационных и ударных нагрузках и при работе в агрессивных средах.
Основные типы подшипников качения:
По форме тел качения
- шариковые
- роликовые
Радиальные шариковые подшипники — наиболее простые и дешевые, допускают небольшие перекосы вала (до 0,25°) и могут воспринимать осевые нагрузки, но меньшие радиальных.
Радиальные роликовые подшипники допускают значительно большие нагрузки, чем шариковые, не воспринимают осевые нагрузки и плохо работают при перекосах вала.
В роликовых цилиндрических и конических подшипниках с бочкообразными роликами концентрация нагрузки от неизбежного перекоса вала существенно снижается. Аналогичное сравнение можно провести и между радиально-упорными шариковыми и роликовыми подшипниками.
Самоустанавливающиеся шариковые и роликовые подшипники применяют в тех случаях, когда допускают значительный перекос вала (до 2…3°), имеют сферическую поверхность наружного кольца и ролики бочкообразной формы. Эти подшипники допускают небольшие осевые нагрузки.
Игольчатые подшипники позволяет уменьшить габариты (диаметр) при значительных нагрузках, воспринимают только осевые нагрузки и плохо работают при перекосе оси.
Кстати дополнительная теория из учебников по технической механике тут.
Муфты
Муфтами — устройства, которые служат для соединения концов валов, стержней, труб, электрических проводов и т. д.
В механике изучают муфты предназначенные для соединения концов валов.
Потребность в соединении валов связана с тем, что большинство машин компонуют из ряда отдельных частей с входными и выходными валами, которые соединяют с помощью муфт. Соединение валов является общим, но не единственным назначением муфт. Их используют для включения и выключения исполнительного механизма (управляемые муфты); предохранения машины от перегрузки (предохранительные муфты); компенсации вредного влияния несоосности валов (компенсирующие муфты); уменьшения динамических нагрузок (упругие муфты) и т. д.
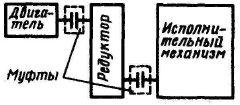
В современном машиностроении применяют большое количество муфт, различающихся по принципу действия и управления, назначению и конструкции. Классификация муфт по этим признакам представлена ниже в виде схемы.
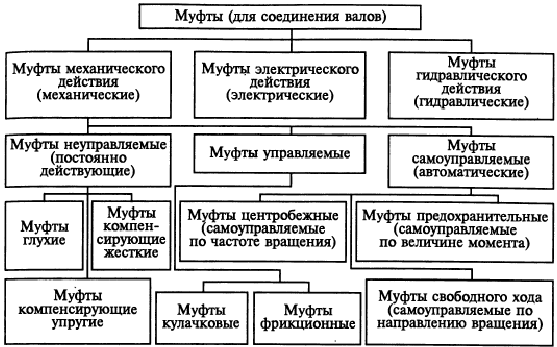
В курсе «Техническая механика» изучают только механические муфты. Широко применяемые муфты стандартизованы. Основной паспортной характеристикой муфты является величина вращающего момента, на передачу которого она рас считана.
Муфты глухие
Глухие муфты образуют жесткое и неподвижное соединение валов (глухое соединение). Они не компенсируют ошибки изготовления и монтажа, требуют точной центровки валов.
Муфты компенсирующие жесткие
Предназначены для компенсации несоосности валов. Вследствие погрешностей изготовления и монтажа всегда
имеется некоторая неточность взаимного расположения геометрических осей соединяемых валов. Различают три вида отклонений от номинального расположения валов:
Муфты компенсирующие упругие
Предназначены для компенсации динамических нагрузок. Включают в себя упругий элемент, который позволяет компенсировать несоосность валов; изменить жесткость системы в целях устранения резонансных колебаний при периодически изменяющейся нагрузке; снизить ударные перегрузки.
[3, c.119]:
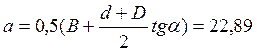
подшипников, α – угол контакта .
Тогда расстояние между точками
приложения реакций подшипников найдём по формуле
[3, c.119]:
мм, где
мм (см.
конструктивную компоновку привода).
8.7
ОПРЕДЕЛЕНИЕ ТОЧЕК ПРИЛОЖЕНИЯ КОНСОЛЬНЫХ СИЛ
8.7.1
ОПРЕДЕЛЕНИЕ ТОЧКИ ПРИЛОЖЕНИЯ КОНСОЛЬНОЙ СИЛЫ
ОТКРЫТОЙ
ПЕРЕДАЧИ
Силу давления ремённой передачи Fоп принять
приложенной к середине выходного конца быстроходного вала на расстоянии lоп от точки
приложения реакции смежного подшипника. Таким образом, из конструктивной
компоновки редуктора мм
9. РАСЧЁТНАЯ СХЕМА ВАЛОВ РЕДУКТОРА
Наметим
силовую схему нагружения валов редуктора, определим реакции в опорах подшипников
валов, построим эпюры изгибающих и крутящих моментов.
9.1 СИЛОВАЯ СХЕМА НАГРУЖЕНИЯ ВАЛОВ
1)
Выбираем направление
винтовой линии червяка. Принимаем правое направление витков червяка.
2)
Определяем направление вращения быстроходного и тихоходного валов редуктора (ω1
и ω2) по направлению вращения двигателя. Так как у нас
привод реверсивный, то направление вращения двигателя можем выбрать
произвольно. Соответственно, направление вращения быстроходного и тихоходного валов
принимаем по часовой стрелке.
Направление
сил в зацеплении редукторной пары изображено на рис. 2 :
T2
ω2
Fr2
Ft2
Ft1
Fa2
Fa1
ω1
T1
Fr1
Рис.2
3) Консольная сила от цепной передачи
Fоп перпендикулярна оси быстроходного вала и направлена вертикально вверх в
соответствии с положением передачи в кинематической схеме привода.
4) Радиальные реакции в подшипниках
быстроходного и тихоходного валов RAx, RAy, RBx, RBy, RCx, RCy, RDx и RDy
направлена противоположно направлению окружных (Ft1 и Ft2) и радиальных (Fr1 и Fr2) сил в зацеплении редукторной передачи.
Таким образом,
схемы нагружения быстроходного и тихоходного валов изображены на рис. 3 и рис.
4 соответственно:
RAy
RBy
Fоп
RA Ft1
RB
Fa1
1 2
3 4
RAx
Fr1 RBx
Рис.3
RCx RDx
1 2
3 4
Fr2
RC RD
RCy Fa2
RDy
Рис. 4
Ft2
9.2
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОПОРАХ ПОДШИПНИКОВ
9.2.1
БЫСТРОХОДНЫЙ ВАЛ
Дано:
Ft1=703,57 Н; Н;
Н;
Н;
м ;
м;
м
(см. п. 5, табл. 2.1, с. 8 – 9).
9.2.1.1
ВЕРТИКАЛЬНАЯ ПЛОСКОСТЬ
В соответствии с рис. 3 (см. п. 9.1,
с. 16) находим RAy и RBy по формулам:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.
Реакции связей — это усилия, с которыми связи действуют на данное тело.
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.
Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.
Реакции гладкой поверхности и ребра
Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям
Рисунок 1.1
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).
Реакции связей нити и стержня
Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).
а – балка висит на двух тросах;
б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»
Рисунок 1.2
Реакции связей шарнирных опор
Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, XA и YA (рисунок 1.3,г).
Рисунок 1.3
Всегда можно перейти от R и α к XA и YA (и наоборот):
Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.
Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).
Рисунок 1.4
В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами XA, YA и RB.
Рисунок 1.5
Подробнее про связи и реакции связей смотрите в нашем видео:
Другие видео
Реакции связи в заделках
Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы RD и момента MD.
Рисунок 1.6
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент MC (рисунок 1.7, б).
Рисунок 1.7
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
Рисунок 1.8
Реакции пространственных связей
Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
Рисунок 1.9
На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
Рисунок 1.10
На следующих рисунках показаны примеры замены различных типов связей их реакциями.
Рисунок 1.11
Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.
Рисунок 1.12
В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.
Рисунок 1.13
Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения
Для пространственной системы — до шести уравнений статики.
Из которых выражаются и рассчитываются искомые реакции.
Пример определения сил реакций связей
Задача
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F2 и F3 приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.
Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.
Решение
Рассмотрим равновесие рамной пластины.
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей XA, YA, RB.
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.
При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие Fx=Fcosα и Fy=Fsinα и учтём что mA(F)=mA(Fx)+mA(Fy).
Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.
Из уравнения (3) находим реакцию катка
Из уравнения (1) горизонтальную реакцию в точке A
Из уравнения (2) — вертикальную.
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.
Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:
Ноль, полученный в ответе, означает правильность составления и решения уравнений
Ответ: Получены следующие значения сил реакций связей: в катке RB=57,6кН, в шарнирной опоре XA=84,96кН и YA=54,2кН.
Другие примеры решения задач >
Проекция силы на ось >



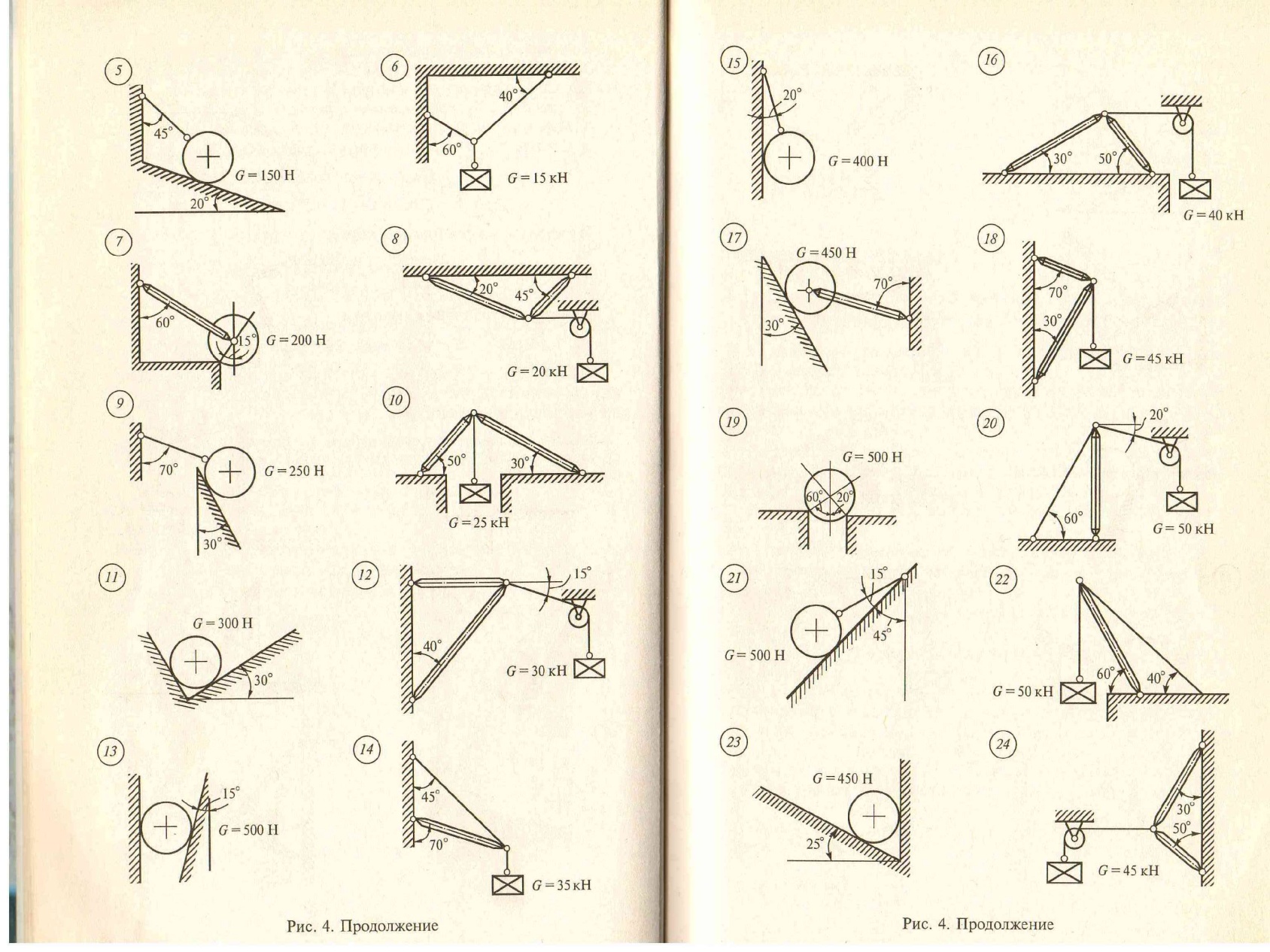

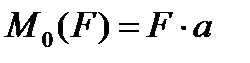


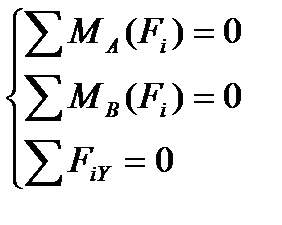
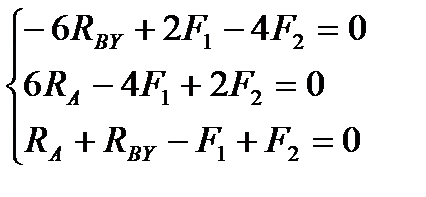









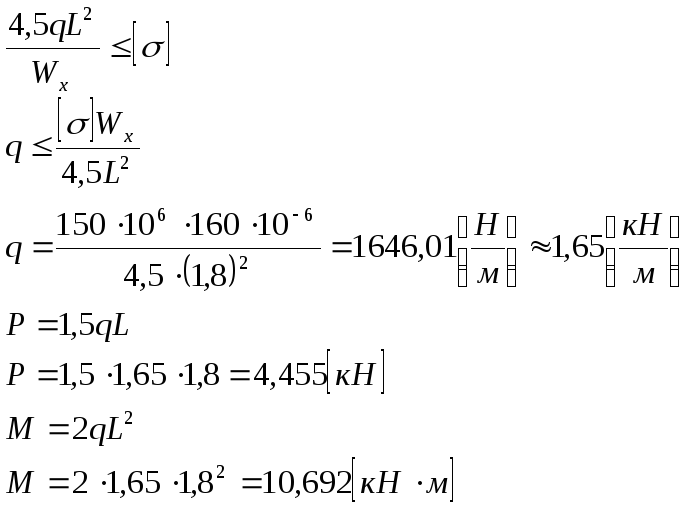






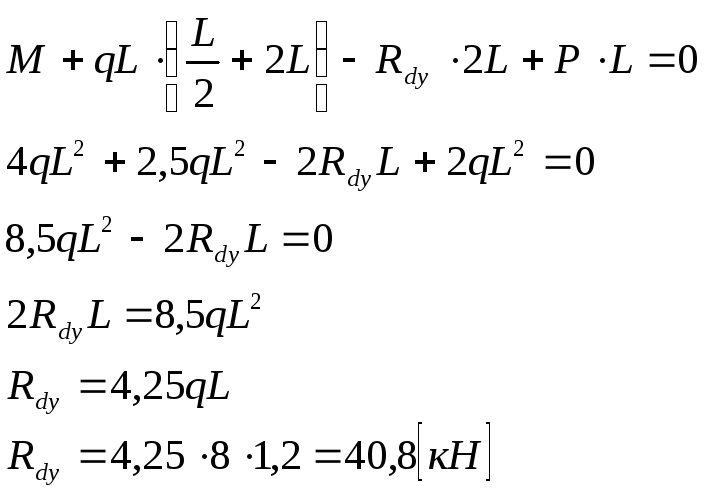



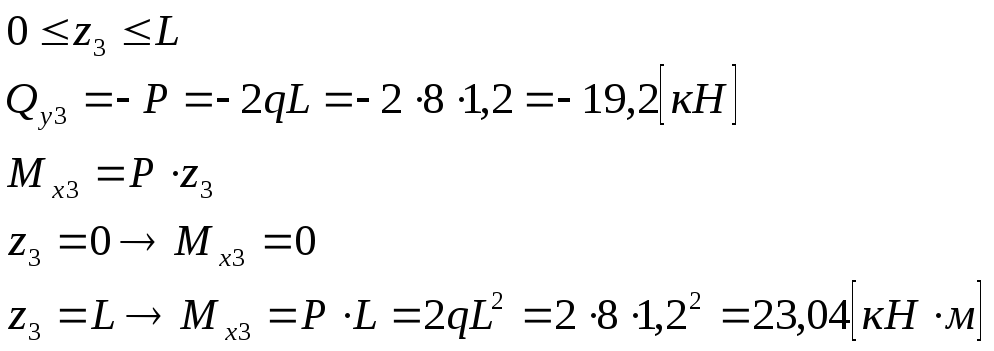






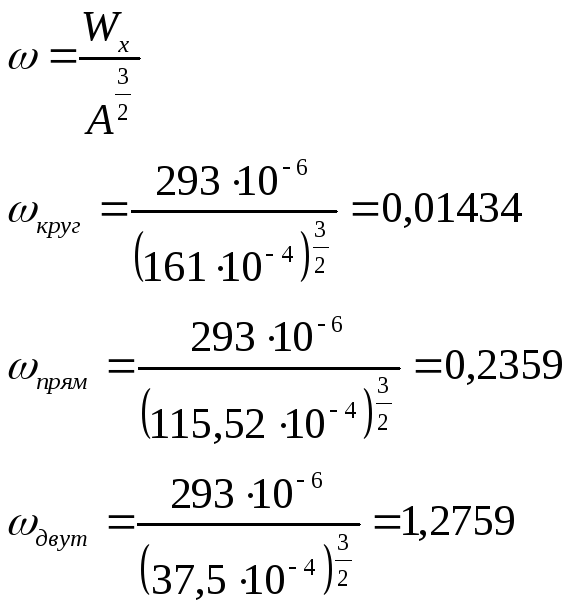




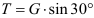
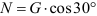
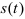
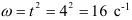
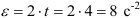
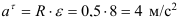
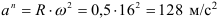
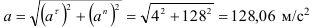
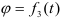
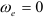 , т.е. в случае поступательного переносного движения.
, т.е. в случае поступательного переносного движения.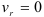 , т.е. в случае относительного покоя точки или в моменты обращения в нуль относительной скорости движущейся точки;
, т.е. в случае относительного покоя точки или в моменты обращения в нуль относительной скорости движущейся точки;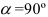 вектор относительной скорости перпендикулярен оси вращения в переносном движении.
вектор относительной скорости перпендикулярен оси вращения в переносном движении.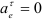
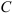
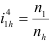
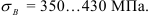
 — отношение нормального напряжения
— отношение нормального напряжения 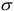 (в пределах
(в пределах 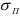 ) к соответствующей относительной продольной деформации
) к соответствующей относительной продольной деформации 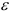 .
.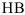 .
.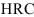 .
. .
.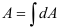
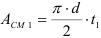
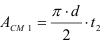
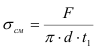
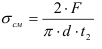
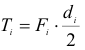
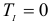
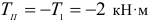
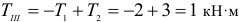
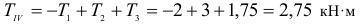
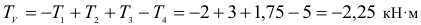
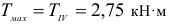
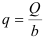
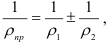
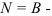
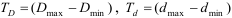
 , в условиях работы которых долговечность подшипников качения резко сокращается (вибрации, шум, большие инерционные нагрузки на тела качения);
, в условиях работы которых долговечность подшипников качения резко сокращается (вибрации, шум, большие инерционные нагрузки на тела качения);